Improvement on the manipulation of a single nitrogen-vacancy spin and microwave photon at single-quantum level
2021-07-06YuanZhouDongYanGuangHuiWangYanHuaFuMingYaoHeandHongTaoRen
Yuan Zhou,Dong-Yan Lü,Guang-Hui Wang,Yan-Hua Fu,Ming-Yao He and Hong-Tao Ren
1 School of Science,Hubei University of Automotive Technology,Shiyan 442002,China
2 Department of of Automobile Engineering,Hubei University of Automotive Technology,Shiyan 442002,China
3 School of Materials Science and Engineering,Liaocheng University,Liaocheng 252000,China
Abstract It remains a great challenge to realize direct manipulation of a nitrogen-vacancy(NV)spin at the single-quantum level with a microwave(MW)cavity.As an alternative,a hybrid system with the spin–phonon–photon triple interactions mediated by a squeezed cantilever-type harmonic resonator is proposed.According to the general mechanical parametric amplification of this in-between phonon mode,the direct spin–phonon and photon–phonon couplings are both exponentially enhanced,which can even further improve the coherent manipulation of a single NV spin and MW photon with a higher efficiency.In view of this triple system with enhanced couplings and the additional sideband adjustable designs,this scheme may provide a more efficient phonon-mediated platform to bridge or manipulate the MW quantum and a single electron spin coherently.It is also hoped to evoke wider applications in the areas of quantum state transfer and preparation,ultrasensitive detection and quantum nondestructive measurement,etc.
Keywords:NV center,mechanical parametric amplification,quantum manipulation
1.Introduction
Implementing quantum manipulations and quantum simulations in the microwave(MW)domain has stimulated huge progress in recent times[1–3].Designing a hybrid quantum system in this special electromagnetic frequency region and implementing efficient quantum information processing(QIP)is gradually becoming recognized as one of the most reliable technological routes[4–7],whereupon the most central task lies in the achievement of perfect manipulation of atoms or artificial atoms utilizing these kinds of MW quantum devices[8],i.e.the MW cavity[9,10],the MW waveguide[11,12],the superconductive circuit[13,14],etc.In addition,it is also regarded as a promising attempt to perform well-controlled quantum measurement or quantum sensing with ultrasensitivity[15,16]through fabricating MW-based hybrid setups or devices[17].With the rapid development of high-quality MW devices integrating technology,the prospect of using MW to dominate QIP is also becoming clearer[18,19].
Regarding today’s mainstream schemes on QIP,and comparing all kinds of quantum units applicable for manipulation,the nitrogen-vacancy(NV)center in diamond is particularly attractive due to its excellent spin properties,i.e.ultrasensitivity to magnetic fields,fast MW manipulation,optical preparation and detection,and long coherence time even at ambient conditions[20–23].The long spin coherence of NVs can also evoke many intriguing applications at the single-photon as well as macroscopic level.For example,it is a high-quality MW emitter in a diamond maser scheme proposed by Jin et al[24],which was also experimentally demonstrated by Breeze group in 2018[25],etc.However,due to the inherent limitation of magnetic coupling mechanism and magnetic field localization degree,it remains a considerable huge challenge to realize a direct strong magnetic coupling to single NV spin in a given MW device[26,27],especially in the MW cavity[28].
In a different way,here we discuss a different approach and propose a hybrid system with phonon-mediated spin–phonon–photon triple interactions,in which a squeezed quantum mechanical mode can not only interact with an NV spin through the first-order gradient magnetic field,but also capacitively couple to the MW cavity[29–32].Utilizing the general mechanical parametric amplification(MPA),we can significantly enhance two pairs of direct spin–phonon and photon–phonon couplings both with the exponential rate(~er)in a new squeezed frame[29,33–38].For a given squeezing parameter r,we can further adjust both coupled pairs to obey the Jaynes–Cummings(JC)-type or anti-Jaynes–Cummings-type interactions,only through modulating the parametersΔc/q.We state bothΔc/qare conveniently tunable parameters with respect to the processes of MW cavity linearization and dressed-state NVs.In view of this hybrid quantum system with adjustable sidebands and enhanced couplings,our scheme may provide a more efficient phononmediated quantum interface to bridge the MW quanta and a single electron spin coherently,and even provide a fruitful route towards the manipulation of a single NV spin and MW photon at the single-quantum level with an improved efficiency.We also hope this result may evoke wider applications in the areas of quantum state transfer[39,40],ultrasensitive detection[41],quantum nondestructive measurement(QND)[42],etc.
2.Setup
The whole schematic design and relevant physical image are all illustrated in figures 1(a)–(c).Working as a mediator,a cantilever-type mechanical resonator(MR)interacts with the MW cavity and a single NV spin,and its spring constant is also periodically tunable,so we can obtain the second-order nonlinear interaction on this mechanical mode[29,38,43–45].In a new squeezed frame,the quantum fluctuation of this MR amplitude is amplified exponentially with~er,known as the MPA[29].As specified in figure 1(a),there are two essential direct strong-coupling parts to form this triple photon–phonon–spin interaction system.For the first part,a sharp nanomagnetic tip is attached at the end of the cantilever with a designed tunable spring constant,just above which a single NV center is set near to this nanomagnet;we can then obtain the strong magnetic spin–phonon coupling with the dressed-state expressionin a squeezed frame[29].We also state another available strain coupling scheme is also equivalent to this magnetic spin–phonon coupling setup,i.e.the investigations[46–50].For the second part,we can also perform the strong coupling through the capacitive interaction between the MW cavity and the MR[32,51].As shown in figure 1(a),a superconducting coplanar cavity is connected to the MR through the capacitor circuit.Then,we can obtain the so-called cavity optomechanical coupling system,and acquire an exponentially enhanced interactionafter the cavity mode is linearized[32,51].
3.Mechanism of this triple coupling system
As illustrated in figure 1(a),we assume that the spring constant of this mechanical cantilever is a periodically tunable parameter with the frequency ωχ.According to the statement in the detail of appendix A,we can obtain the Hamiltonian of this quantized cantilever with the second-order nonlinear interaction


Figure 1.(Color online)(a)Potential photon–phonon–spin hybrid setup with respect to the triple coupling system mediated by a squeezed mechanical mode.A sharp nano magnetic tip is attached at the end of the silicon cantilever with its tunable spring constant,above which a single NV center is set near to this magnet.A superconducting coplanar MW cavity also couples to this mechanical cantilever through capacitive interactions.As a result,it is available for this MR to achieve capacitive coupling to the MW cavity and magnetic coupling to the single NV spin,respectively.(b)Schematic of enhancing the indirect coupling between the MW cavity and single NV spin through MPA.(c)Ground-state energy diagram for a single NV center in the basis of bare state and dressed state.
In equation(1),we have discarded the energy-shift item caused by this nonlinear drive amplitude Ωχ.
According to figure 1(c),for the first NV–MR coupling pair,we apply the dichromatic MW fields to dress the ground state of the NV center,and acquire the efficient spin–phonon transition channel according to appendix B.In a selected dressed-state subspace{|d〉,|g〉},the effective spin–phonon interaction can be rewritten as the JC-type Hamiltonian

For another pair of MR–cavity coupling,we assume the MW cavity interacts with the MR capacitively,which forms the so-called cavity optomechanical coupling pair.This type of interaction is described as
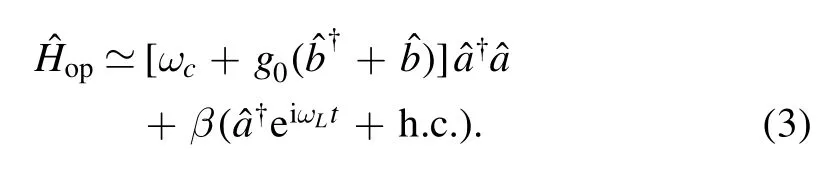
In equation(3),the first two items describe the general optomechanical coupling with the fundamental cavity frequency ωcand the optomechanical coupling strength g0,and the last item means the classical MW laser drive to this cavity mode with driving amplitude β and frequency ωL.Utilizing the standard linearization method withand=α*+[32,51],we can linearize this optomechanical interaction(3)as
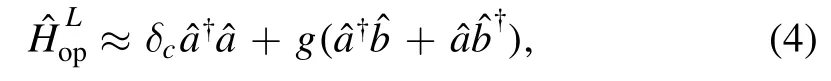
in which the parameters are assumed as δc=ωc-ωL,α*=α,and g=g0α,and we have setfor simplicity.
As a result,together with equations(1),(2),and(4),we can obtain the whole Hamiltonian for describing this phononmediated three-body hybrid system:
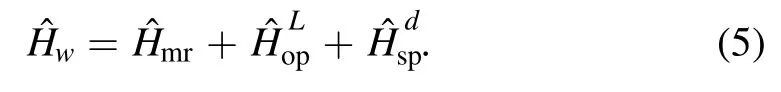
Then,we apply an unitary transformationto equation(5)withIn this new rotating frame,we can obtain

with δm=ωm-ωχ,Δc=δc-ωχ,andΔq=ω0-ωχ.
Considering this Hamiltonian(6)accompanied by the second-order nonlinear interaction of this mechanical freedom,we can utilize the standard unitary transformationto diagonalize this mechanical mode belonging towhere the squeezing parameter r is defined by tanhIn this squeezed frame,we can obtain the Hamiltonian with the new expression
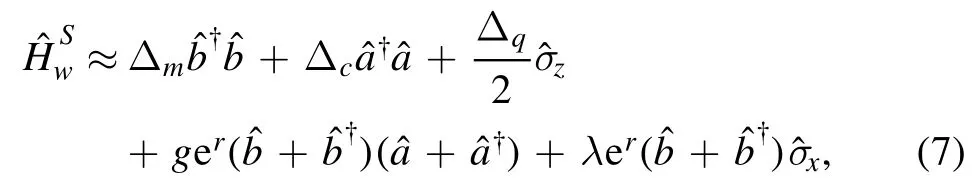

with G1=ger,G2=λer,δ1=Δc+Δm,δ2=Δc-Δm,δ3=Δq+Δm,and δ4=Δq-Δm.For a realistic condition,the dynamical evolution of this hybrid system is dominated by the master equation effectively as follows:
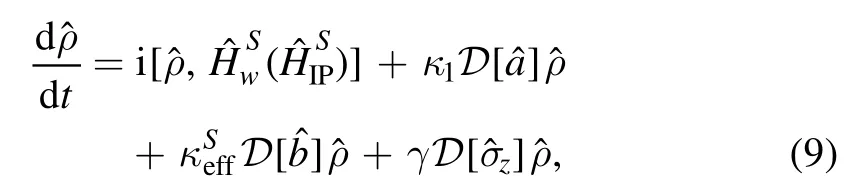
In this squeezed frame,the mechanical mode is fast and strongly damped with a large effective dissipation rate[38,52].In this case,we can inevitably maintain this phonon mode in its ground state|0〉and neglect the populations of any excited modes.This squeezed mechanical mode is then considered as an artificial or engineered reservoir of the heat phonon.In contrast,we can also apply an auxiliary cooling system or design to suppress its effective dissipation rate at the same magnitude as~κ1,according to investigations[52–56].
Considering Hamiltonian(8),we also note,for a given cantilever with a certain squeezing parameter r,thatΔmis very small and untunable.However,ΔcandΔqare both tunable parameters,which can be implemented via the cavityresonator linearization process and NV-resonator MW dressed process.Through modulating both relevant parameters,we can obtain an effective triple Hamiltonian with distinct expressions.Utilizing this,we can also carry out different simulations for multiple applications.For example,in case(i),whenΔc-Δm≃Δq-Δm≃0,the Hamiltonian reduces to the beam-split-type interaction effectively,withwhich is applicable for establishing a quantum interface to bridge the MW photons and NV spin efficiently.In case(ii),when Δc+Δm≃Δq-Δm≃0(orΔc-Δm≃Δq+Δm≃0),the Hamiltonian reduces to the types ofwhich is suitable for engineering the MW photons and NV spin into the nonclassical steady states,such as certain entanglement or quantum correlation.In case(iii),onceΔc+Δm≃Δq+Δm≃0,the Hamiltonian is also reduced to the form+h.c.effectively,which can also be applied to the preparation of special nonclassical states;i.e.governed by this type of interaction,an investigation on generating the Bell-type maximum entanglement through a fast dissipation process was recently reported[57].Taking cases(i)and(ii)as examples,we present specific discussions and numerical simulations of relevant applications in the following section.
4.Applications
4.1.Efficiency improvement on quantum state transfer between the NV spin and MW photon
For case(i),the effective Hamiltonian reduces to
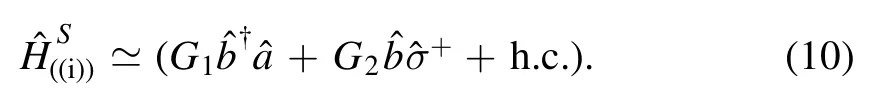
Utilizing this interaction,we can implement the target of quantum state transfer from the MW photons to an NV spin mediated by this squeezed phonon mode,and vice versa[39,40].Therefore,the first application of this scheme is focused on establishing a quantum spin–photon interface with further improved efficiency.
For an ideal condition without considering any decoherence factors,this triple-interaction system is governed by the Schrödinger equationTaking the quantum state transfer from the MW photon to NV spin at the singlequantum level as an example,we first assume this photon mode is reduced to the lowest subspace{|0〉,|1〉}for simplicity.Without loss of generality,the initial state of the MW cavity is assumed as|ψ〉MW=α|0〉+β|1〉with the normalizing condition|α|2+|β|2=1,and the mechanical mode and NV spin are both initialized in their ground states|0〉mand|g〉s.Therefore,the initial state of this whole system is initialized in the assumed state|Ψ(0)〉=|ψ〉MW⊗|0〉m⊗|g〉s,and the relevant quantum information to be transferred to NV spin is initially coded in the freedom of this MW mode with the given coefficients α and β.
Here we assume g≃λ and G1=-G2=G=gerfor simplicity,and this whole system is dominated by Hamiltonian(10).Through solving this Schrödinger equation,we can obtain its evolved state|Ψ(t)〉analytically at any arbitrary time t.At the special moment with τs~π/G=π/(ger),we can obtain the target state with|Ψ(τs)〉=|0〉MW⊗|0〉m⊗|ψ〉sand|ψ〉s=α|g〉+β|d〉.Then,we can reach the target of transferring the arbitrary quantum information of MW mode to NV spin and vice versa.Furthermore,its transfer efficiency will be further improved significantly by this squeezed mechanical mode owing to the amplification of both coupling strength and rate er[29].
To indicate this physical process more clearly and intuitively,we need to carry out the relevant numerical simulation on it.Considering all adverse decoherence factors in our numerical simulation,its dynamical evolution is governed by the master equationIn general,here we set α=0.6,β=0.8,κ1~γ~0.01g,and~0.1g for simplicity;then,we can solve this master equation numerically and achieve dynamical fidelity according to the definitionnamely the overlap between the target state|Ψ(τs)〉and the dynamically evolved statesat arbitrary moment t.
The corresponding numerical results are plotted in figure 2,and these numerical results are highly consistent with our analysis above.We note that the fidelity can be near to 1 infinitely in the first few periods of oscillation in time,regardless of whether the squeezing parameter is set as r=1,r=3,or r=5,and even with all of the decoherence factors being considered in this master equation.In addition,the relevant state-transfer efficiency and velocity can also be further improved significantly as we increase the squeezing parameter r from r=0 to r=5,and its shortest time interval for transfer satisfies τs∝e-r.
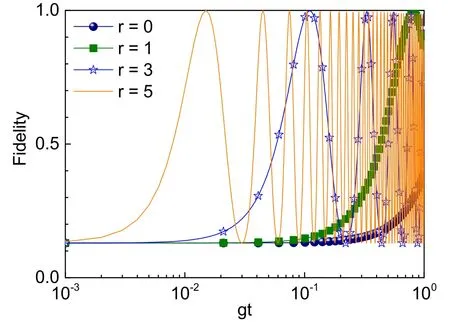
Figure 2.(Color online)Dynamical fidelity for this photon–spin state transfer process.The parameters are set as g=λ,r=0 the black solid line with solid spheres,r=1 the olive solid line with solid squares,r=3 the blue solid line with open stars,and r=5 the orange solid line,κ1~γ~0.01g,and ~0.1g.
4.2.Engineering NV spin and MW photon into the quantum correlated state indirectly by the squeezed phonon mode
In contrast,for case(ii),the effective Hamiltonian obeys the forms of
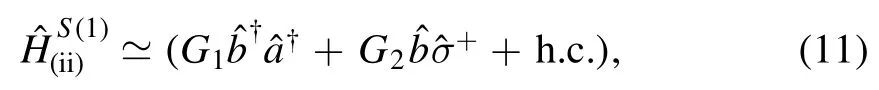
or

Dominated by both types of triple interactions,we can also carry out the task of engineering the MW photon and NV spin into the steady nonclassical state,utilizing different routes such as the adiabatic evolution or fast dissipation,etc[38,52,57–60].Taking Hamiltonian(11)as an example,we first assume G1is opposite to G2in phase and G1≠G2;then,we can rewrite this Hamiltonian asWe note this type of interaction is quite similar to the general Hamiltonian for engineering the two-mode quantum correlated state assisted by fast dissipation[60–63].In this scheme,we stress that the photon–phonon and spin–phonon coupling can be exponentially enhanced in a squeezed frame;however,the realistic dissipation rate of this squeezed phonon mode will be inevitably amplified without any additional cooling design.To engineer this pair of NV and MW photon into the relevant nonclassical state,we are confident that the fast dissipation route is a more suitable choice in this scheme.

The results in figure 3 clearly show that,for a given squeezing parameter r=2,we can achieve an entangled steady state of this pair of NV spin and MW photon as the whole system is dynamically evolved to the moment of~10/g.We also note that this steady state is not the maximum entanglement,and all three different characterizations are highly consistent with our analysis above.Therefore,although there is no direct strong interaction between this pair of NV spin and MW cavity,they will be fast-engineered into a steady quantum correlated state with the assistance of this strongly damped MR.This type of application may also provide another efficient route toward the manipulation of a single NV spin with an MW photon at the single-quantum level.

5.Experimental estimations
To examine the feasibility of our scheme in realistic conditions,we now discuss the relevant experimental parameters.We consider a silicon cantilever with dimensions(l=11,w=0.05,t=0.04)μm;the fundamental frequency and the zero-field fluctuation can be expressedMHz anda0=respectively[67–73],the quality factor of this mechanical mode is estimated as about Qm∈[103,106]with Young’s modulus E~1.3×1011Pa,the mass density ϱ~2.33×103kg/m3,and the effective mass of this magnet-attached cantilever resonator is estimated as m~1.4×10-17kg[72,74,75].With the rapid development of advanced nanotechnology,the first-order gradient magnetic field caused by the nanomagnet is expected to reach near Gm~106T/m,and we can also obtain that the magnetic coupling strength between the MR and NV spin satisfies g∈2π×[1,100]kHz[74,76,77].On the other side,the fundamental frequency of this MW cavity with quality more than 107is also estimated as ωc∈2π×[1,20]GHz[3,4,18,19].
6.Conclusion
Addressing a key scientific challenge with respect to realizing direct manipulation of an NV spin at the single-quantum level with an MW cavity,we propose a hybrid system with spin–phonon–photon triple interactions,mediated by a squeezed quantum harmonic resonator.Applying the general MPA to this in-between phonon mode,we can exponentially enhance both direct spin–phonon and photon–phonon couplings,which can even further improve the coherent manipulation of an NV spin and MW photons with higher efficiency.In view of this three-body system with enhanced couplings and adjustable sidebands,this scheme may provide a more efficient phonon-mediated platform to bridge or manipulate the MW quanta and a single electron spin coherently.We also hope it can evoke wider applications in the areas of quantum state transfer and preparation,ultrasensitive detection,QND,etc.We stress that this proposed scheme is general and can be applied to others electron spins[78],such as silicon-[79,80],germanium-[81],and tin-vacancy centers[82],and its original magnetic spin–phonon coupling mechanism can also be applied in other devices with strain coupling or electric coupling[46–48,50,83,84].
Acknowledgments
Y.Z.is supported by the National Natural Science Foundation of China under Grants No.11 774 285,No.11 774 282,and No.11 504 102,the Natural Science Foundation of Hubei Province under Grants No.2020CFB748,and No.2019CFB788,the Research Project of Hubei Education Department under Grants No.D20201803,No.B2020079,and No.B2020078,the Doctoral Scientific Research Foundation of Hubei University of Automotive Technology(HUAT)under Grants No.BK201906,and No.BK202008,and the Foundation of Discipline Innovation Team of HUAT.H.T.R.is supported by the the Doctoral Scientific Research Foundation of Liaocheng University under Grant No.318 052 054.Parts of the simulations are coded in PYTHON using the QUTIP library[64,65].
Appendix A.Realizing the second-order nonlinear interaction of this MR
The main mechanism and physical image of this proposal is illustrated in figures 1(a)and(b).Working as an in-middle mediator,the Hamiltonian of this MR with a time-dependent spring constant is described as




Appendix B.Magnetic coupling of the MR to an NV center in the dressed-state basis
For the second spin–phonon coupling part,this vibrating magnet tip produces the time-dependent gradient magnetic fieldBg(t)=Bgcosωmtand then acts on the NV spin magnetically,with the gradient magnetic field vector components Bg=(Bx,By,Bz),and the MR fundamental frequency ωm.Here,we note ωm(~MHz)is much smaller than the NV ground-state transition frequency(D±δ/2~GHz);these faroff resonant interactions between the NV spin and the gradient magnetic fields along the x and y directions are negligible.In the rotating frame at the frequency ωm,the Hamiltonian for describing the magnetic interaction between the mechanical mode and the single NV center is
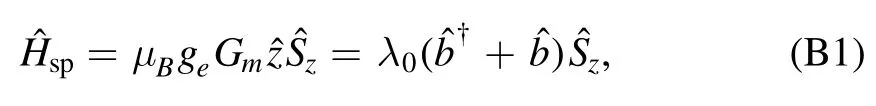
where λ0=μBgeGmzzfis the magnetic coupling strength with the Bohr magneton μB=14 GHz/T,the NV Landéfactor ge≃2,and the first-order magnetic field gradient Gm=∂Bz/∂z.As illustrated in figure 1(c),in the bare-state basis,we can not achieve the effective spin–phonon transition interaction because of ωm≪D±δ/2,but we can utilize the dressed-state method to resolve this problem.




ORCID iDs
杂志排行
Communications in Theoretical Physics的其它文章
- Intermediate symmetric construction oftransformation between anyon and Gentile statistics
- Proton radioactivity within the generalized liquid drop model with various versions of proximity potentials
- Joule–Thomson expansion of higher dimensional nonlinearly AdS black hole with power Maxwell invariant source
- Notch fatigue of Cu50Zr50 metallic glasses under cyclic loading:molecular dynamics simulations
- Eigen microstates and their evolutions in complex systems
- Non-similar mixed convection analysis for magnetic flow of second-grade nanofluid over a vertically stretching sheet
