基于随机优化算法的建筑热环境灰箱模型开发与验证

2021-07-05曹子涵明岭峰陈焕新王汝金

制冷技术 2021年2期

曹子涵，明岭峰，陈焕新*，王汝金

（1-华中科技大学中欧清洁与可再生能源学院，湖北武汉 430074；2-华中科技大学能源与动力工程学院，湖北武汉 430074；3-压缩机技术国家重点实验室（压缩机技术安徽省实验室），安徽合肥 230031）

0 引言

由于建筑物系统和外界环境系统本身的复杂性，难以直接分析优化控制建筑节能的具体措施，因此分析建筑能耗的一个关键技术是建立建筑热传递模型[1]。

物理模型，俗称白箱模型，具有精度高的优点，但模型比较复杂，建筑的物理特征难以获取；数据驱动模型，俗称黑箱模型，需要大量的数据进行训练，导致数据的采集工作成本高，且精度难以保证。若将物理模型和数据驱动模型相结合，可以得到一种能代表建筑系统的物理特征，同时结构简单、可信度高的模型。灰箱模型，是一种介于白箱和黑箱模型的简化模型，其研究对象的特征与关系不是完全清晰的，一部分物理特征数据可以直接测取，另一部分难以获取的特征则通过数据训练得到，这种模型是进行建筑分析、诊断及优化控制等的首选。

热阻-热容（Thermal Resistance and Heat Capacity，RC）网络模型[2]是一种典型的灰箱模型。邵双全等[3]提出了基于多输入多输出结构的室内外机自适应控制策略，建立自适应控制算法，说明了采用计算机仿真实现多联式空调系统的控制策略的优化的可行性。赵浩亮等[3-4]提出利用建筑信息模型对异形空间的空调负荷进行分析计算，介绍了应用建筑信息模型（Building Information Modelin，BIM）计算空调负荷的方法，并和传统空调负荷计算方法做了对比。结果分析表明，建筑信息模型的应用是可行的。WANG等[5]提出的基于遗传算法的建筑物动态模型内部热质参数估计，结果表明，具有集总建筑物内部质量的简化模型具有良好的稳定性；OGUNSOLA等[6]采用指数矩阵法简化状态空间方程，分析求解热网络模型，用于空气调节系统（Heating，Ventilation and Air Conditioning，HVAC），以便准确估计加热和冷却负载。刘涛等[7]采用基于改进天牛须算法-优化极限学习机能耗预测模型，对地源热泵进行能耗预测。结果表明该模型能显著提高能耗预测精度，说明了机器学习在能耗预测领域的优势。BRAUN等[8]开发了一种用于瞬态建筑物负荷预测的逆灰箱热网络模型，来预测建筑物的瞬态冷却或加热要求。RAMALLO等[9]基于热网络模型，通过创建3R2C（三个热阻和两个热容）模型来表示多层结构，保留主导层模型（Dominant Layer Model，DLM）而忽略次要的层次，可以达到较高精度；LIAO等[10-11]开发了一种建立简化二阶物理模型的方法，以模拟住宅建筑现有多区域供热系统的动态行为。

本文构建的模型为3热阻-3热容（3 Thermal Resistance and 3 Heat Capacity，3R3C）模型，具有三阶传递函数，精度和鲁棒性更好。通过合理的假设和构建的RC模型，结构简单、精度可靠、能够准确描述建筑环境内外能量的交互关系。同时，采用随机优化算法（遗传算法[12]和粒子群算法[13]）来求解模型的优化问题，通过不断地迭代求解模型求得数值解，避免复杂矩阵的逆与分解运算，保证计算精度的同时降低了计算成本。

1 基于随机优化算法的3R3C模型

1.1 3R3C模型

由于物理模型和数据驱动模型各自优缺点非常明显，故首选灰箱模型对建筑构建RC热网络模型。为了有效描述建筑环境内外能量的交互关系，RC网络模型分为边界条件、模型输入和模型输出这3部分[3]，这就可以将建筑环境的能量模型中的消耗能量和储存能量模块类比为电学领域的电阻R和电容C[14]。

建筑热环境主要组成部分是建筑外壳、室内蓄热单元、冷却或加热源和虚拟空气处理单元。建筑物系统的简化网络模型是物理建模和数据驱动型建模的结合，建筑物具体详细的物理特征可以直接使用；无法获得的物理特征，则对其进行假设。假设的参数通过已知的物理描述和运行数据确定。

运用集总参数[9,15]，构建建筑系统的3R3C网络模型，考虑建筑围护结构、室内空气空间和室内的蓄热单元3个方面，其中建筑的围护结构主要是指外墙，建筑的内部结构主要包括地板、隔板、内墙、天花板和家具等蓄热材料，模型中的3个电阻和电容的值视为未知的常量，需通过模型辨识得到。

根据建筑的模型示意图，运用整个建筑的能量平衡得到的节点微分方程组可表示为：

式中，Cw为围护结构等效电容，F；Cim为室内空气等效电容，F；Cin为内部质量等效电容，F；Tw为维护结构温度，℃；Tim为结构室内空气温度，℃；Tin为空气内部质量温度，℃；Rw为围护结构等效电阻，Ω；Rim为室内空气等效电阻，Ω；Tout为室外的天气温度，℃；Qsolar为太阳辐射热能，℃；Qc为建筑室内空调系统的给冷量或热量，J；Qin为室内长波辐射量，J。

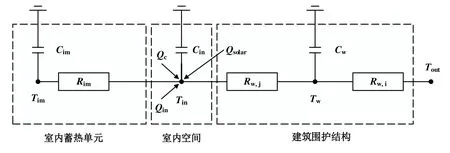
图1 3R3C网络模型

1.2 基于随机优化算法的建筑内部质量参数确定

3R3C网络模型内部质量参数的确定是基于随机优化算法得到最优的3个电阻和3个电容（即Rw,i、Rw,j、Rim、Cw、Cim和Cin的值）。执行随机优化算法应先确定好模型的目标函数，运用回归技术[16]，使得模型的预测结果最符合实际情况。确定模型参数Rw,i、Rw,j和Rim以及Cw、Cim和Cin的目标，使模型按微分方程计算出的室内温度Tin与实际室内温度Tin,exact的差异最小，实际室内温度通过EnergyPlus仿真得到。度量误差最小化的目标函数为均方根误差，公式为：

使得目标函数最小化是一个优化问题，而实现优化的方法有很多种。比如工程数值计算有牛顿下山法[17]，还有LM法[18]、BFGS[19]和L-BFGS[20]等，都可以用于求解该优化问题。但是这些算法涉及到求解矩阵的梯度以及矩阵的求逆和矩阵分解，对工程应用而言不太友好。而随机优化算法，不需要做这些复杂矩阵的逆和分解，运用4阶龙格库塔法，求解节点微分方程组以不断地求解模型，不断地迭代求解，使目标函数最小化，这不涉及到复杂的矩阵运算。工程中采用随机算法的可能性更高，计算也比较高效。

1.3 运用四阶龙格库塔法进行参数估计

先根据简化的3R3C网络模型，结合建筑系统能量平衡列出模型的节点微分方程组。对于初始化一组模型参数的数据，可以通过运用四阶龙格库塔法求解微分方程组得到模型预测的室内温度Tin，进而求得目标函数值，为使得目标函数值最小化，运用随机优化算法，主要是遗传算法和粒子群算法，不断迭代和更新模型的参数，以达到最优解。

3R3C网络模型的参数估计的具体步骤：1）开始运行，设定好的阈值epsilon和最大迭代次数Num；2）在合理的估计范围内，先初始化3个热阻和3个热容的值；3）次数i=1，运行随机优化算法得到热阻热容值；4）运用四届龙格库塔法求解微分方程组得到模型预测的室内温度Tin值；5）再结合EnergyPlus仿真得到的室内温度Tin,real，即可算出误差（方差或算术平均误差），记录当前最佳的适度函数值或目标函数；6）再判断终止条件1，当前迭代次数是否达到最大迭代次数，若没有就加1，并运行随机优化算法，再返回步骤4、步骤5和步骤6，反之，次数达到要求就执行步骤7；7）再判断终止条件2：连续两次得到的最佳参数值之差是否小于等于阈值epsilon，若大于则返回步骤2、步骤3、步骤4、步骤5和步骤6继续执行，反之输出此时3个热阻和热容值的结果，即得到模型的参数值。

图2 3R3C网络参数估计流程

2 随机优化算法下的3R3C模型

2.1 建筑系统数据来源

为了方便简化模型和验证模型的正确性，本文使用EnergyPlus仿真一个长8 m、宽5 m、高3 m的房间，相应的建筑能量变化数据也基于此房间。

仿真得到的数据共计3,072组，将数据集按照时间段排序，并划分为训练集和验证集。训练集数据用于训练3R3C网络模型得出模型的最佳参数，验证集数据用于验证模型的鲁棒性。为了避免训练出的模型出现欠拟合和过拟合的情况，将现有数据集复制为两个副本。第一个数据副本训练集大小为前2,000组，剩下为验证集数据；第二个数据副本的大小为前2,500组，剩下为验证集数据，第二个数据副本中用于训练模型的数据占比较大。每个数据副本均执行模型的参数估计代码。执行遗传算法时，最大进化代数为400代，初始化种群的大小为100，粒子的惯性参数W=0.9，学习因子C1=0.5、C2=0.3。

2.2 模型预测的室内温度与仿真的室内温度比较

通过训练后，模型预测求得的热阻参数值如表1所示，热容参数值如表2所示。

表1 训练后模型预测求得的热阻参数值

表2 训练后模型预测求得的热容参数

第1份数据副本的训练集执行遗传算法和粒子群拟合的室内温度的情况如图3所示。除少数时间点上，模型预测的室内温度与EnergyPlus仿真的室内温度相差2～5 ℃，大部分两者的结果相当接近，差异均在1 ℃之内。

图3 第1份数据副本的训练集模型预测的室内温度与EnergyPlus仿真室内温度对比

在最大迭代次数相同和初始种群或粒子群的大小相同的情况下，运行遗传算法或粒子群算法，在第1份数据副本的训练集下得到的模型参数基本一样，各自的目标函数相差不大。但实际执行时，运行遗传算法较粒子群算法耗时、计算成本较高。

第2份数据副本的训练集执行遗传算法和粒子群拟合的室内温度的情况如图4所示。大部分时间，模型预测的室内温度与EnergyPlus仿真的室内温度相差2～5 ℃之内，两者的结果相当接近均方根误差为1.5 ℃左右。当最大迭代次数相同和初始种群或粒子群的大小相同的情况下，运行遗传算法或粒子群算法，在第2份数据副本的训练集下得到的模型参数基本一样，各自的目标函数也相差不大。且实际执行时，运行遗传算法计算成本相对较高，这与数据副本的结论相互印证。因此粒子群算法较遗传算法在此3R3C网络模型上适用性更好。

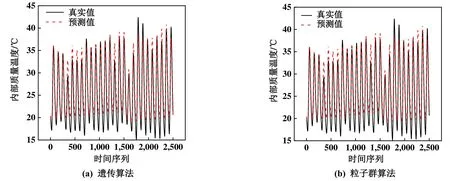
图4 第2份数据副本的训练集模型预测的室内温度与EnergyPlus仿真室内温度对比

3 验证模型的鲁棒性

3R3C网络模型确定后，需要检验新数据运用时模型的预测能力。如果模型预测的室内温度与EnergyPlus仿真得到的室内温度相差比较小，预测的精度在可接受范围之内，说明该模型具有较好的鲁棒性。否则需重新检查步骤或重新构建网络模型，再进行模型的重新辨识。

执行不同算法的两组数据误差情况如表2所示。验证集模型预测的室内温度与仿真值的拟合情况如图5和图6所示。

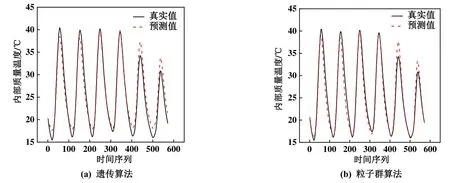
图6 第2份数据副本的验证集模型预测的室内温度与仿真值的拟合情况

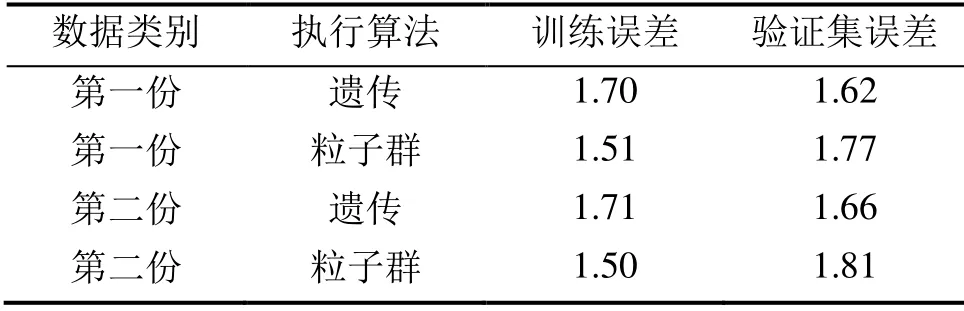
表2 误差情况

图5 第1份数据副本的验证集模型预测的室内温度与仿真值的拟合情况

由图5和图6可知，当EnergyPlus仿真的室外天气温度在35 ℃以上时，3R3C网络模型预测的室内温度普遍比仿真结果小，且温度越高，预测的温度误差越大，最大的接近5 ℃，在35 ℃以下时，3R3C网络模型预测的室内温度接近EnergyPlus仿真的室内温度，结果误差均在±1 ℃之内。说明两种算法的辨识都具有较好的鲁棒性。