基于脉冲耦合神经网络的异源图像融合方法
2021-07-05范训礼李晓艳孙梦宇乔梦雨
张 宽, 王 鹏*, 范训礼, 李晓艳, 孙梦宇, 乔梦雨
(1.西安工业大学 电子信息工程学院,陕西 西安 710021; 2.西北大学 信息科学与技术学院,陕西 西安 710127;3.西安工业大学 光电工程学院,陕西 西安 710021; 4.陕西航天技术应用研究院有限公司,陕西 西安 710100)
依托于当今信息时代大背景,人们能够通过声、光、图像等多种同/异介质传感器,综合信息融合技术来获得相对于单一传感器而言更为丰富现场信息。图像作为人类肉眼能够直接感知的信息类型,与人类日常生活息息相关,因此与之相关的融合日渐增多,可见光与红外图像融合便是当下主流研究方向之一[1-2]。融合图像既能发挥红外射线对热目标敏感、探测距离远、穿透能力强等优点,又能保持微光/可见光图像对比度高、细节丰富、与人眼特性相近等明显优势[3-5]。深入研究可见光与红外图像融合能够用于军事作战、遥感影像分析、红外检测、防恐怖安全检查、军事观测等应用领域,同时亦有利于图像后续处理(如检测、识别、跟踪等),为其提供图像基础,因此也有着重要理论研究意义。
无论在频域还是时域,小波变换对于信号的局部特征均具有良好的表达能力,基于此,Chipman等[6]人提出的基于小波变换的图像融合方法在当时获得了广泛的关注,但该算法的融合规则过于简单,并不能很好地利用其表达能力;2014年,Naidu等[7]提出了小波变换(Wavelet Transform,WT)与主成分分析法(Principal Component Analysis,PCA)结合的图像融合方法,能够更好地保留空间细节信息,但由于PCA会受到大噪声的影响,从而导致估计结果误差偏大,最终影响图像融合质量;2018年,江泽涛等[8]提出了基于改进型脉冲耦合神经网络(Improved Pulse Coupled Neural Network,IPCNN)的红外与可见光图像融合算法,将图像的高低频信息分别进行融合,针对高频信息,该算法采用IPCNN进行融合,但针对低频信息的融合方法较为简单,故对低频信息的表达不够完善;2020年,Guo等[9]提出了基于全卷积网络的图像融合算法,该算法通过数据集来训练全卷积网络,从而完成图像融合任务,但训练过程较为复杂,并且对设备性能要求较高;2021年,Zhang等[10]与Jiang等[11]分别提出了基于NSST和提升LSCN的图像融合算法与基于纹理分析的IPCNN的融合算法,两种方法均将信号分为高频部分和低频部分,针对高频或纹理信息部分均采用脉冲耦合神经网络(PCNN)进行融合,这样能够较好地保证融合质量,但对低频信息并未进行噪声分析。
本文结合了小波变换和PCNN的优点,提出了基于鲁棒性主成分分析法(Robust Principal Component Analysis,RPCA)与PCNN的融合方法。对源图像进行小波变换后,将高频信息送入PCNN中进行融合,以保证图像细节融合质量;对于低频信号,采用RPCA的方法对其进行融合,采用非精确增广拉格朗日乘子法对其进行优化求解,保证融合图像的保真度和求解效率;最后采用逆小波变换得到最终的融合图像。
1 基于主成分分析与二代小波变换的图像融合方法
此方法中,首先是将已配准的可见光图像进行主分量变换[12];再对可见光图像的第一主分量与近红外图像进行提升小波变换[13](Lifting Wavelet Transform,LWT)融合处理,其中,高低频的融合规则均采用了加权平均的融合规则;用融合结果代替可见光图像的第一主分量,其目的就是既要融入近红外图像的细节信息,又要保留可见光图像的光谱信息;最后,对得到的可见光图像3个新主分量做逆变换,从而得到最终的融合图像。使其在多光谱信息的保持与空间细节表现的综合性能得到提高。
在此,假设矩阵A表示信号矩阵即为高频信号矩阵与低频信号矩阵,且同时为低秩矩阵,矩阵E为标准差为σ的白噪声矩阵,矩阵D为观测矩阵,则传统的PCA算法的优化模型为
(1)
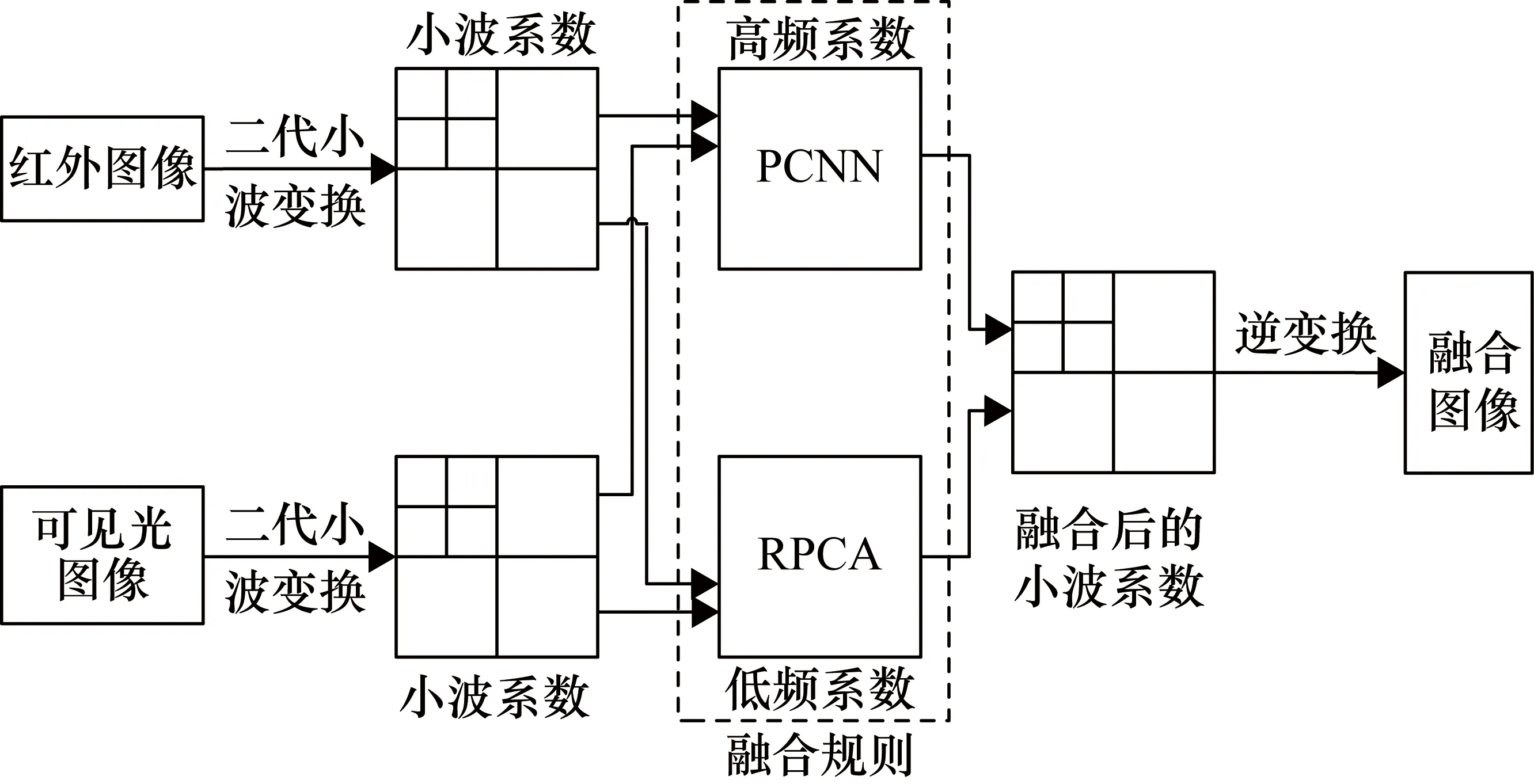
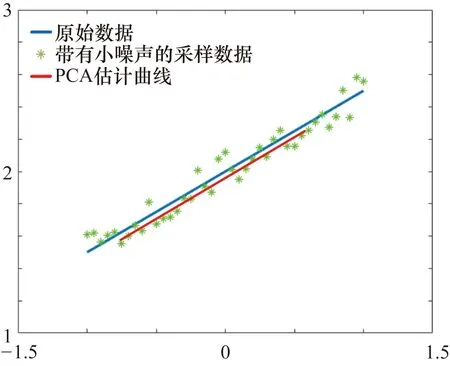
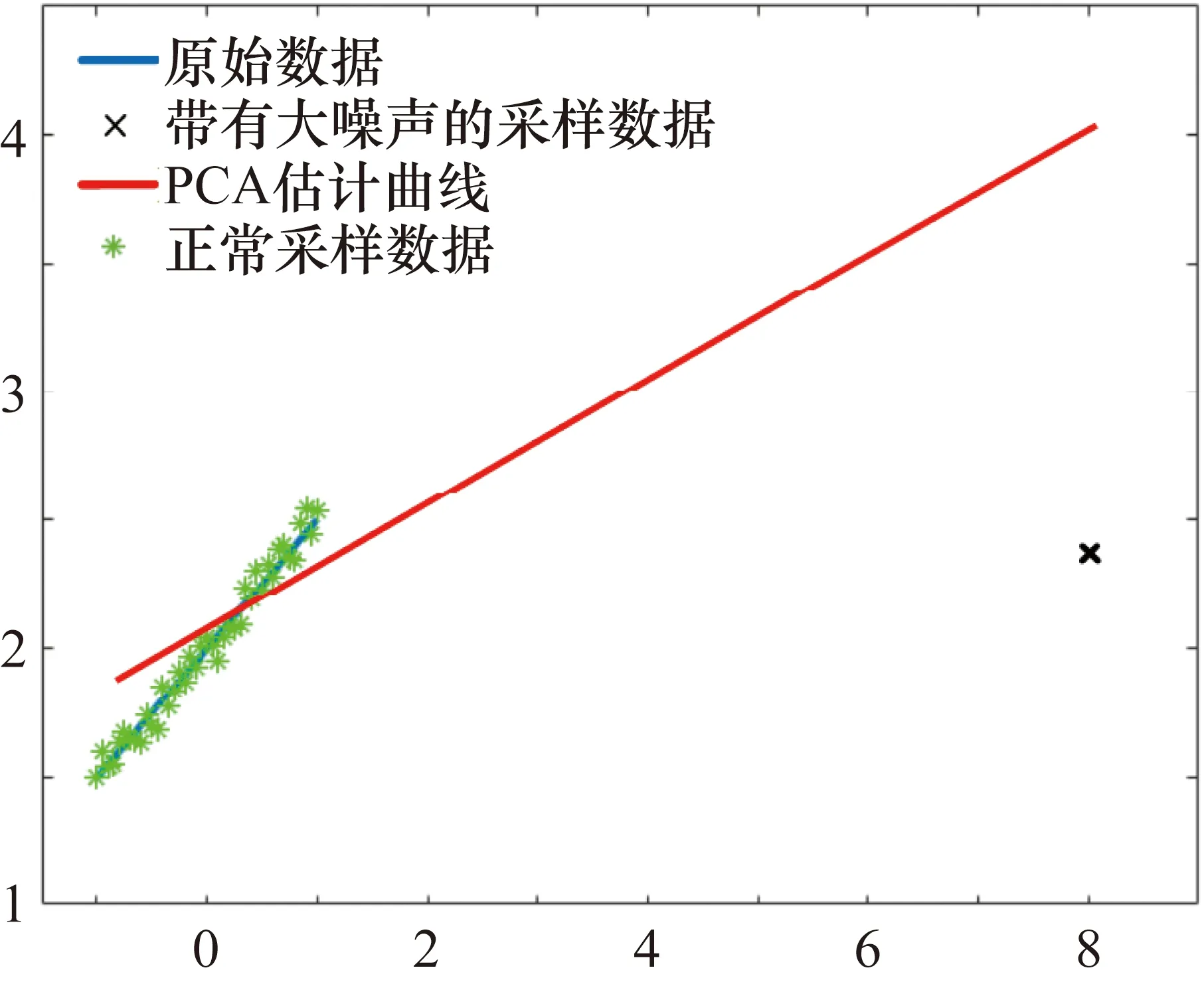
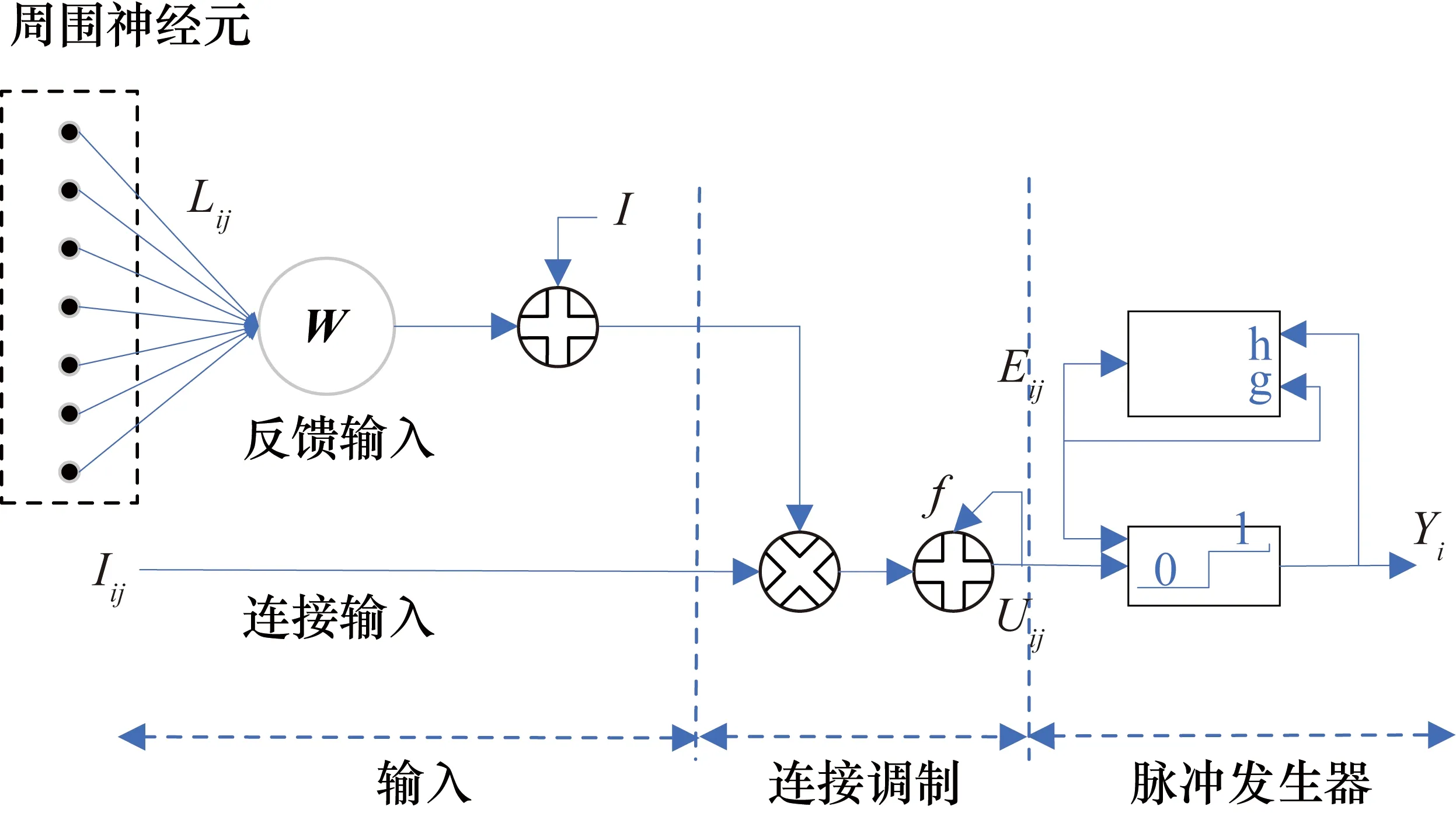
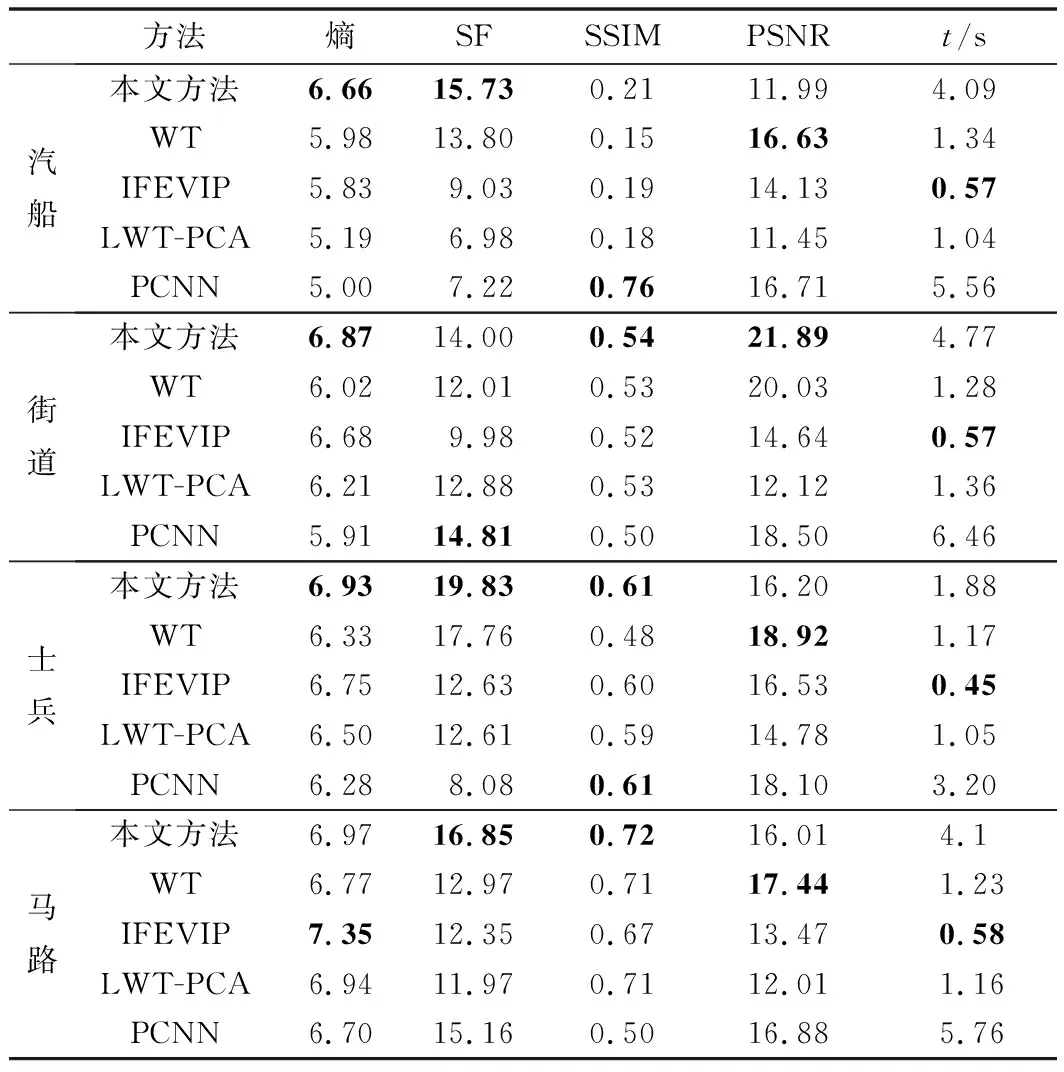
式中,ρ(·)为矩阵的秩;r为预定的目标维度,且满足条件r< 第二代小波变换——提升小波的步骤流程如图1所示。 图1 提升小波步骤流程图 ① 分裂。分裂部分负责将原始信号sj分成偶数样本和奇数样本,分裂过程为 F(sj)=(sj-1,dj-1) (2) 式中,sj-1为低频近似分量;dj-1为高频近似分量;F(sj)指分解过程。 ② 预测。此步骤需要利用数据之间的关系,构造预测算子,使用偶数样本预测奇数样本。预测误差计算方法为 dj-1=dj-1-P(sj-1) (3) 式中,P(·)为预测算子。 ③ 更新。此步骤通过更新算子U(·)生成一个更好的数据集sj-1来保留原始数据集sj的一些特征。分解过程为 sj-1=sj-1+U(dj-1) (4) 由于LWT是完全可逆的,因此LWT的反变换与LWT具有对称的结构,相比之下,可以准确地重建图像。 对源图像的高频信号和低频信号采用加权平均的的融合规则即可形成融合后的高频信号和低频信号。 在信号出现较大的误差时,PCA无法准确恢复信号,而红外与可见光图像又是光谱特性差异很大的两种图像,传统基于PCA与LWT的融合方法在此时便不太适用。另外,该算法在高频图像信息部分并未做针对性处理,因此最终获得的融合图像难免受到PCA算法本身局限性的影响[14]。基于以上所述,为了提高传统基于PCA与LWT融合的鲁棒性,使其更适用于多源图像融合领域,同时增强融合图像的细节表达能力,引入了RPCA与PCNN算法,提出了基于鲁棒性主成分分析与脉冲耦合神经网络的图像融合方法。 其中,RPCA[15]能够很好地解决传统PCA鲁棒性差的缺点;而PCNN[16]是学者们在研究猫等哺乳动物的视觉神经元时受到启发而提出来的,该算法在原理上较为符合人类视觉成像原理,因此能够通过该算法在图像中提取出满足人类肉眼观察的丰富细节信息。 算法步骤具体如下:首先,将红外与可见光图像进行二代小波变换,将两种图像各自分解为高低频信号;其次,对低频信号采用RPCA完成融合,用以提高算法的鲁棒性,利用非精确增广拉格朗日乘子法还原低秩矩阵,对还原后的低秩矩阵采用加权平均的方式进行融合;然后,高频信号则输入至PCNN中进行融合,以提高融合后的图像质量;最后,将融合后的小波系数进行逆变换,便可获得最终的融合图像。 整体方案图如图2所示。 图2 整体方案图 主成分分析法[15]经常被用于传统的图像融合方法中,尤其在信号噪声较小时能够获得很好的估计结果,但当出现某一较大的噪声时,PCA无法准确估计信号,图3和图4展示了当信号噪声小以及出现了较大的噪声时PCA方法的估计结果,图中横纵坐标仅仅代表数值大小,无其他实际意义。 图3 小噪声估计结果 图4 大噪声估计结果 可以看到,图3中采样数据噪声较小,传统的PCA方法能够很好地估计出原本的信号曲线,图4中出现了严重错误的数据,此时PCA的估计结果偏差较大,无法准确还原真实数据。因此,拟采用RPCA[16]以解决传统融合方法鲁棒性较低的问题。 (5) 此时,观测矩阵的低频小波系数矩阵可以表示为 (6) 此时求解公式可以写为 (7) 在此假设Y为迭代的拉格朗日乘子,μ为用于调节计算效率与精确度平衡的参数,因此构建的增广拉格朗日乘子函数为 (8) 将其划分为两个子问题迭代求解,公式为 (9) (10) (11) 式中,Dε为奇异值阈值算子。 (12) (13) 两个矩阵迭代求解直至收敛。 对于引入的拉格朗日乘子Y和参数μ在每次迭代过程中的更新如式(14)所示: (14) 根据式(6)、式(12)、式(13),更新后的观测矩阵数学公式如式为 (15) 在融合低频小波系数中,采用了加权平均的方法,当两张融合图像相似程度较高时,此方法十分有效,而本文采用了RPCA的方法,具有较好的保真度和一致性,因此加权平均的方法将会起到较好的效果。 传统算法采用小波变换进行图像分解与融合时,虽能够较好地保留概貌信息,但细节信息略显不足,因此,对高频信息采用PCNN[17]进行融合。首先介绍了高频子带图像的融合策略,之后对PCNN进行简要介绍。 所采取高频融合策略具体如下。 可见光与红外图像分别经过提升小波分解后,各自都会转换为多幅高频子带图像和一幅低频子带图像;将高频子带图像作为输入图像,分别送入简化版PCNN中,由此可以得到多个点火序列图;接下来将根据高频子带图像相应位置的点火图来判断最终的高频子带系数,具体判断方法是:如果两张相应异源高频子带图像中相同位置的点火图的值小于某个阈值(例如,经1层分解后的水平方向上的高频可见光图像和红外图像可被视为相应异源图像,其他分解层数与水平方向上的图像同理),此时算法认为空间上两点的灰度值相似,取两者灰度的算术平均值作为该点的高频子带融合系数;如果该点的点火图的值大于某个阈值,则认为两点的灰度值不相似,此时取点火值较大的点的灰度值作为该点高频子带融合系数。由此得到所有的高频子带融合系数。 最后,将低频信息与高频信息结合,通过小波逆变换即可得到最终融合后的图像。 PCNN算法实质上是一种无监督的单层神经网络,图5为由学者简化版本的PCNN单个神经元模型框图[18],其基本原理与标准PCNN算法相同,只是简化了多余的参数,模型的数学表达式如式(16)所示。整个模型由输入部分、连接调制部分、脉冲发生器部分三部分构成。 图5 简化版PCNN单个神经元模型框图 首先,神经元模型会在接收域采集邻近神经元信号和外部输入激励信号。这两种信号在模型中通过两种不同的路径进行传递,分别为L路径(邻近神经元信号)和F路径(外部激励信号);接收到两个信号后,神经元模型会在连接调制部分通过累加和调制操作完成两个信号的耦合,耦合的结果被称为内部活动项;PCNN模型中,脉冲发生部分由一个脉冲发生器和比较器构成,其中,比较器的阈值大小能够变化。在该模型运行过程中,如果内部活动项达到比较器中所设定的阈值大小,此时神经元被称为点火状态。在该状态下,脉冲发生器将发出一个特殊的频率不变的脉冲信号。 (16) 式中,(i,j)为输入的神经元序号,在图像处理中为对应的像素点位置;n为系统的迭代次数;Uij(n)为神经元的内部行为;f用于控制Uij(n)衰减,取值范围为0~1;Iij(n)为神经元的外部激励(常取图像的灰度值或者像素所在区域的特性指标);W为神经元之间的连接权系数矩阵;Ypq为邻域神经元的输出;Eij(n)是变阈值函数输出,其控制神经元的点火阈值;g为阈值衰减系数;h为阈值放大系数;Yij(n)为第n次迭代神经元的输出状态,其由Uij(n)和Eij(n)大小关系共同决定,当Yij(n)=1 时称神经元发放一次脉冲或者完成一次点火。 将PCNN应用于图像融合,此时每一个PCNN神经元对应于图中单个的像素点,这些像素点彼此互为周围神经元,这样就能够形成一个单层二维PCNN,同时这也意味着算法在构建PCNN时,神经元的个数应当与输入图像像素数量相当。输入某张图片至该网络时,算法首先需要对图片中各个像素点的灰度值进行归一化处理,这样才能作为外界刺激信号去激励各个神经元。而外部刺激越强,对应神经元的点火频率就越高。当某一神经元(对应于单个像素点)点火成功,而各神经元又是彼此耦合链接,因此会导致周围神经元在这时的内部活动项的值发生变化,若最终该值大于阈值,则某一个周围神经元也将点火,输出脉冲。与此同时,随着某一点神经元点火,其内部活动项对应的阈值也会随之增加,因此该神经元不会一直不停地输出脉冲。最后,随着该像素点的点火次数不断累加,脉冲次数也在不断增加,最终算法能够得到一张反映各个像素点点火次数的图像,被称为点火图,它包含有图像的区域、边缘、纹理等信息,能够为后续图像处理提供重要信息。 本文中设置的PCNN参数数据参考于文献[19],该数据是通过大量实验总结而来的经验数值,具体为:内部活动项的初始值为0;动态阈值初始值为1;f为0.2;g为0.9;h为20;n为3;W为 此选择定量与定性两种分析方法,并选择了4个同场景下的可见光与红外图像进行融合实验,将本文算法与其他4种算法进行了对比试验。为保证实验的公平性,所有算法均在Window 10 操作系统、Intel®CoreTMCPU i7-7700HQ 2.8 GHz 8GB内存计算机上采用Matlab 2018a软件进行仿真实验。 所采用的用于融合的4组可见光与红外图片组来源于网络公开的TNO Human Factors数据集,该数据集包含不同军事相关场景的多光谱夜间图像,每一组可见光与红外图像组都经过严格的配准,因此可以被直接应用于图像融合研究。 对比了5种不同的算法,即本文算法、IFEVIP(Infrared Feature Extraction and Visual Information Preservation)算法[20]、WT算法、LWT+PCA算法和PCNN算法,经5种算法处理后的融合图像以及运行结果如图6所示。 图6 结果对比图 从图6中可以看到,4种算法均能保留源图像中的背景信息,同时也能够准确提取目标信息。但WT算法虽能够提取到目标信息,但目标边缘和细节不够明显,主要原因在于WT算法对高纬度的边缘信息表达能力较差,对奇异信息表达更好;IFEVIP算法和LWT+PCA算法更多地保留了可见光图像信息,而IFEVIP算法的对比度更高,但在汽船图片中明显看到,其对于船体边缘很小的目标并未显示,并且空中分界线也未能够显示出来。LWT+PCA算法却可以较好地融合这两种信息,但整体而言,该算法对于背景信息的体现还是不够好。例如,在汽船图案中,在天空背景亮度方面,该算法明显示不如IFEVIP算法能反映真实背景亮度。而对于单独使用PCNN的融合图片,与其他方法相比,该算法得到的图片亮度都略低;与除WT算法之外的算法对比,该算法不够突出目标的轮廓信息;但是从细节信息的角度而言,该方法用于汽船与士兵图案中,能够看到清晰的船体边缘与树叶的形状,这与PCNN的细节表达能力比较强有关。而所提出的方法融合图像对比度高,目标边缘足够清晰,结构信息足够丰富,例如汽船图片中的小型目标和边界线、街道图片中的牌匾文字、士兵图片中的栅栏等均能够看清,原因在于本文所采用的RPCA方法能够从背景中准确分离提取目标,边缘清晰,利用PCNN的高频融合能够保留较好的细节信息。从定性实验综合来看,本文所提出的算法的可见光与红外融合图像效果最好,视觉效果最佳。 本文选取了4种指标对比了5种算法的表现,具体指标如下。 ① 熵[21](Entropy)。熵表示该融合图像中信息含量的多少,熵值越高,表示包含信息越丰富。熵值计算公式为 (17) 式中,pl为融合图像中该灰度的归一化灰度值;L为灰度数量。 ② 空间频率[22](Spatial Frequency,SF)。空间频率是根据图像梯度指标对图片质量放假行评价的指标,通过对图像中梯度的测量,可以表示图像的细节纹理的丰富程度,空间频率越高,表示细节越丰富。其计算公式为 SF= (18) 式中,i和j为图像的索引值;F为图像的灰度值;M和N分别为目标的长和宽。 ③ 结构相似度[23](Structural Similarity,SSIM)。结构相似度表示两张图之间的相似度,计算公式为 (19) 式中,X和F分别为源图像与融合图像;σ为图像的协方差矩阵;μ为图像的均值;C1、C2、C3为中间变量,用于稳定测试算法,当C1=C2=C3=0时,此指标为通用指标。 ④ 峰值信噪比[23](Peak Signal-to-Noise Ratio,PSNR)。峰值信噪比度量是融合图像中峰值功率与噪声功率的比值,反映了融合过程中的失真程度。该值度量定义为 (20) 式中,r为融合后图像的峰值。PSNR越大,融合图像越接近源图像,融合后的图像失真越小。 本文所测试的4种算法的测试结果如表1所示。表1中,粗体字表示该方法在此指标下性能最好。对于熵指标而言,所提出的算法仅仅在马路图片序列中的测试结果落后于IFEVIP算法,排在第2位,在其他测试图片中均为第一名。PCNN算法表现最差,对于每张融合测试图片,由该算法得到的融合图片的熵值都为最低。但实际上,各个算法的熵指标性能测试数据相差并不太大,最大差值数据体现在汽船图片的测试结果中,分别是本文算法的6.66和PCNN算法的5.00,最大差值为1.66,其他的数据差别都小于该值,大多相差不超过1。因此,由熵指标测试结果可以得到的结论是相对于其他4种算法,本文算法在获取源图像的信息量方面略强于其他算法,但其实各个算法本身在该方面的性能相仿。 表1 定量测试仿真结果表 在空间频率指标方面,除街道图片中略逊于PCNN算法外,本文算法在其他测试图片中的表现均为最好,且由各个算法间的数据差值能够看出,本文算法相对其他算法提升较大。在该指标中,PCNN的值变化较大,最低时候仍旧是5个算法中效果最差的,但最高的时候比本文算法都好,远强于其他算法。另外在该指标测试数据中,IFEVIP算法和LWT-PCA算法的数据值相对稳定,但表现较差。因此,相对于其他算法,本文算法能够获得较为丰富的细节信息,并且表现稳定。 在结构相似度指标中,对比熵指标的数据结果不难看出,本文算法与其他算法在两个指标中的表现类似。说明本文算法生成的融合图像与源图像相似度更高。但各个算法在此方面的性能相差不大。 而在峰值信噪比的指标中,本文算法在各个测试图片中的测试结果中,排名处于中上位置,仅次于WT算法;同时远远超过LWT-PCA算法,该算法是对比算法中在峰值信噪比指标测试中表现最差的。与其相比,本文算法在失真程度上要小很多。另外在算法运行速度方面,本文算法较为耗时,在各个测试图片中,均表现不佳,但略强于普通PCNN算法,因为采用了多尺度变换,整个PCNN不需要对整张源图像做相关运算,而是仅对高频子带图像做相关运算。 整体而言,由表1可以看出,相对于以上其他4种融合算法,本文算法在接近一半的测试结果数据中排在第1位,这部分数据主要集中于熵指标、空间频率指标和结构相似度指标;另外在峰值信噪比指标测试中也有较好的表现,仅次于WT算法;最后在运行时间指标中表现一般,算法运行所需时间仅低于PCNN算法。试验结果表明,与上传统LWT-WT算法相比,经本文算法融合后的图像中熵指标、空间频率指标、结构相似度指标和峰值信噪比指标均有不同程度的提高,其中空间频率指标和峰值信噪比指标差距提升最大,说明了本文算法的先进性和有效性。 本文提出了基于RPCA与PCNN的图像融合算法,利用RPCA的优势,更好地提取目标信息,使得融合图像中目标的边缘更加清晰;将LWT分解出的高频信息利用PCNN进行融合,因此本文所提出的算法融合后得到的图像具有更好的视觉效果,并且相关指标皆有明显提升,证明了算法改进的有效性。另外,所提出的算法亦有待提高,例如在峰值信噪比指标测试结果中,经本文算法融合后的图像的PSNR值落后于WT算法;相对于上述对比方法,本文算法由于采用复杂度较高的PCNN算法,因此在计算速度方面会落后于其他算法。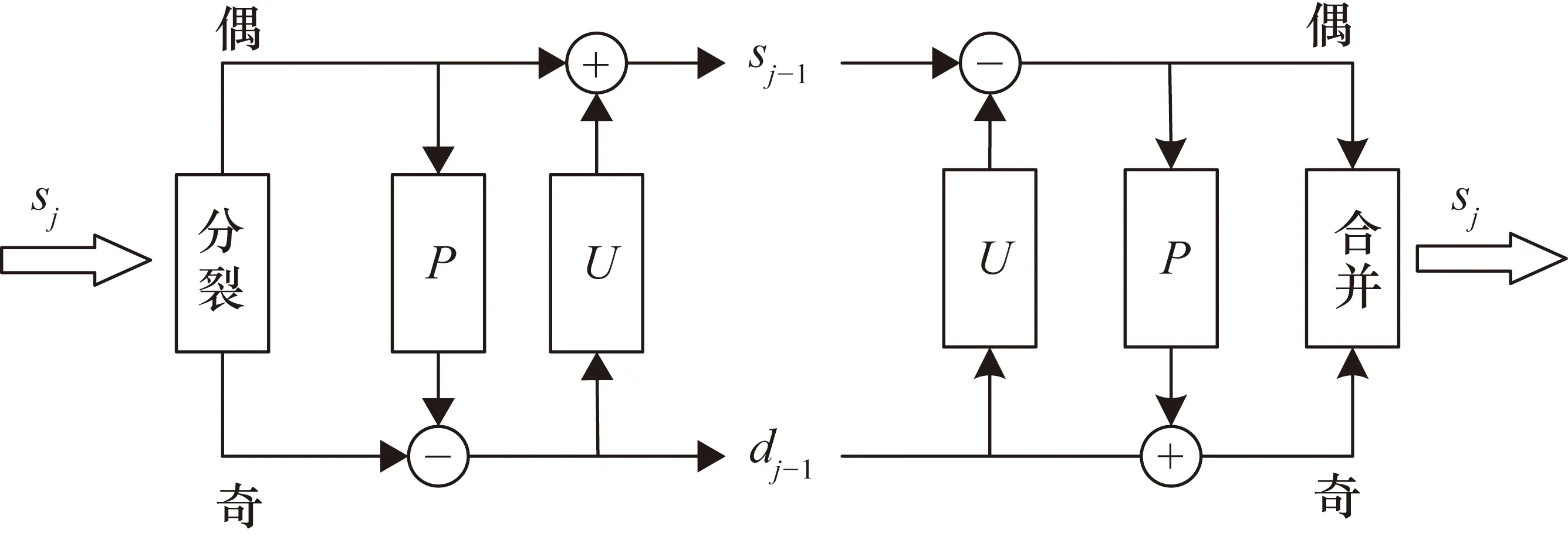
2 基于鲁棒性主成分分析与脉冲耦合神经网络的图像融合
2.1 基于鲁棒主成分分析法的低频融合策略
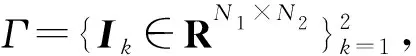

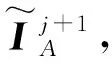
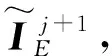
2.2 基于脉冲耦合神经网络的高频融合策略
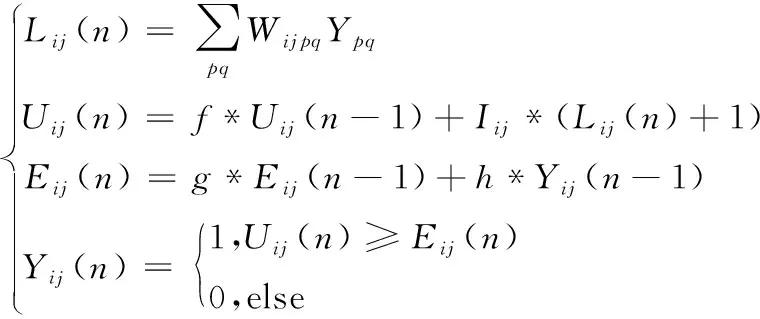

3 实验
3.1 定性分析

3.2 定量分析
4 结束语
