刚性卵形弹丸对半无限厚铝合金靶的穿深方程

马铭辉,王晓东,蒋招绣,余毅磊,李 烨,高光发

(南京理工大学 机械工程学院,江苏 南京 210094)

预测弹靶的相互作用是一个非常复杂的问题,当弹丸侵彻目标靶板时,弹靶的动态响应会随着弹靶材料的强度、靶板厚度和弹体结构的变化而变化[1-2]。而当刚性弹侵彻靶板时,靶板中会形成一个与弹丸结构相似的弹坑,且弹坑的深度受到弹丸头部形状和弹丸着靶速度的影响。目前,对于刚性弹侵彻目标靶板的侵彻深度问题已有较多的研究。BISHOP等[3]建立了弹塑性固体中圆柱形和球形空腔的准静态膨胀方程,对圆锥形射弹侵彻金属靶板时所受的力进行了估算;基于BISHOP的空腔膨胀模型,FORRESTAL等[4-5]建立了工程模型,用来预测不同弹头形状的刚性长杆弹对不可压缩弹塑性目标的穿透方程,并通过对6061-T651铝合金靶板的末端弹道试验发现,球形弹头的理论模型与试验结果十分吻合,而卵形和锥形弹头的偏差较大;同时,FORRESTAL等[6]建立了刚性长杆弹对应变硬化材料的穿深方程,发现侵彻过程中弹丸与靶板材料之间的滑动摩擦阻力对模型预测的准确性有较大影响;王晓鸣等[7]对FORRESTAL的经典阻力公式中的静态阻力项进行了修正,发现修正后的模型能明显提高侵蚀的计算精度;文献[8-9]提出了一种基于动态腔体膨胀模型的通用无量纲公式,在一定速度范围内能够较好地预测卵形刚性弹对金属、混凝土和土壤的穿透深度。目前,对于刚性弹侵彻金属靶板的侵深计算,主要是基于球腔膨胀或者柱腔膨胀模型推导出弹体在侵彻过程中所受的阻力,进而通过积分得到最终的侵彻深度[10-13]。基于圆柱形腔膨胀理论,将尖头刚性弹穿透目标装甲并形成柱腔所需要的能量等效为弹丸动能,可以确定弹丸对目标装甲的弹道极限[16]。

本文通过改进刚性弹穿透目标靶板的能量方程,进一步得到半无限厚铝合金靶在刚性卵形弹丸侵彻作用下形成腔体所需要的能量,将腔体膨胀所做的功近似等效为弹丸的动能,最终计算得到刚性卵形弹对目标靶板的侵彻深度。通过开展对3种不同类型(2A12,6061,7075)的半无限厚铝合金靶板的侵彻试验,得到了不同入射速度下刚性卵形弹对3种靶板的侵彻深度,利用上述方法对刚性卵形弹的侵彻深度进行计算,并与试验结果进行了比较,进而对方程的准确性进行验证。

1 穿深方程

铝合金靶板在受到射弹冲击后的主要破坏模式为韧性扩孔,这种可延展的孔洞增长机制可以用HILL[15]的圆柱形扩孔模型来简化穿孔过程,圆柱形空腔近似将目标理想化为垂直于穿透方向压缩的薄的独立层,因此,分析过程可以简化为沿靶板径向方向的一维运动。根据TAYLOR[16]的柱腔膨胀理论,弹丸对靶板所做的功可以等效为弹丸将靶板从零初始半径扩展到弹丸穿透靶板后形成的柱腔半径所做的功:

WDHF=πh0r2Cσ

(1)

式中:r为孔的最终半径,在数值上等于弹芯的半径;h0为弹丸所贯穿的靶板的厚度;σ为靶材中孔边缘的径向应力;常数C为形状因子,定义了扩孔边缘的厚度,C=h/h0,h为弹丸穿透靶板后所形成的柱腔的总高度(翻唇高度与靶板厚度之和)[16]。

当刚性弹侵彻半无限厚靶板时,可以将腔体膨胀做功等效为靶板材料经塑性变形形成弹坑所耗散的塑性功,根据式(1),塑性功为

W=πPer2σ

(2)

式中:W为靶板变形所耗散的塑性能,Pe为弹坑的等效深度。对于半无限厚的铝合金靶板,其受到刚性卵形弹冲击时的破坏模式为延性扩孔,并且侵彻过程中弹体与靶板材料紧密贴合,因此圆柱形空腔的半径r等于弹体的半径rp。靶板迎弹面有轻微的翻唇,翻唇高度相较于弹坑深度可以忽略不计,因此忽略了翻唇部分耗散的塑性功所带来的影响。由于侵彻结束后的弹坑形态并非是完全的圆柱形空腔,而是与弹体形态相似(头部为卵形,主体为柱形),因此式(2)中的弹坑等效深度Pe(弹体卵形头部完全侵入靶板的情况下)为

Pe=P-lh+le

(3)

式中:P为弹坑的最终侵彻深度,lh为弹体卵形头部的长度,le为弹体卵形头部的等效长度。

(4)

式中:mp,ρp,rp分别为弹体的质量、弹体密度和半径;l为弹体的总长度。对于式(1)中的孔边缘径向应力σ,有许多公式对其进行了定义[16-18]。FORRESTAL等[18]将σ定义为在平面应变条件下靶板形成圆柱形腔所需的准静态径向应力σS:

(5)

(6)

(7)

式中:Y和E分别为靶板材料的屈服应力和杨氏模量,n为应变硬化指数,用于拟合LUDWIK[19]应力-应变ε曲线:

(8)

式(6)在x=0处具有奇异性,但是,这种奇异性可以通过展开式对积分进行求值,不需要在端点处求积。将式(3)～式(5)代入式(2),可得:

(9)

由参考文献[20]的有限元模拟可知,刚性弹丸侵彻铝合金靶板过程中弹靶的接触面几乎无摩擦,因此不考虑摩擦做功所消耗的能量,最终弹丸的动能等效为靶板所做的塑性功,即:

(10)

式中:v0为弹丸的初始速度,则最终侵彻深度P的方程为

(11)

根据球腔膨胀方程[19],对刚性弹侵彻过程中的轴向阻力进行推导,最终得到侵彻深度P与入射速度v0的关系为

(12)

(13)

式中:ρt为靶板密度,ψ为卵形弹头的曲率半径。弹体卵形头部系数为

(14)

基于空腔膨胀模型,将腔体膨胀做功等效为弹丸的动能,推导得到了刚性卵形弹对铝合金靶板的穿深方程(11)。将穿深方程中所需要的各个参数的值分别代入方程(11)和方程(12),最终分别得到2个模型下的侵彻深度与弹丸入射速度的关系。

2 靶板材料力学性能试验

穿深方程中各个参数的确定需要对铝合金靶板材料的力学性能进行测试。利用密度仪分别测量3种铝合金材料(2A12T4,6061T6,7075T6)的质量密度,得到它们的密度分别为2.77 g/cm3,2.71 g/cm3,2.81 g/cm3。利用MTS万能试验机,在应变率为0.001 s-1下对3种铝合金靶板材料进行准静态压缩实验,得到它们的真实应力-应变曲线如图1所示。

选取残余应变为0.2%时的应力值作为材料的屈服强度,得到3种铝合金材料的屈服应力和杨氏模量如表1所示。

针对药学院校和相关专业量大面广、实验室类型多样、缺乏有针对性的安全环保教育与管理的现状，借鉴国外药学院校与实验室管理模式与经验，结合笔者在实验室安全环保管理工作中发现的问题，从教、学、管、监四方面提出如下建议。

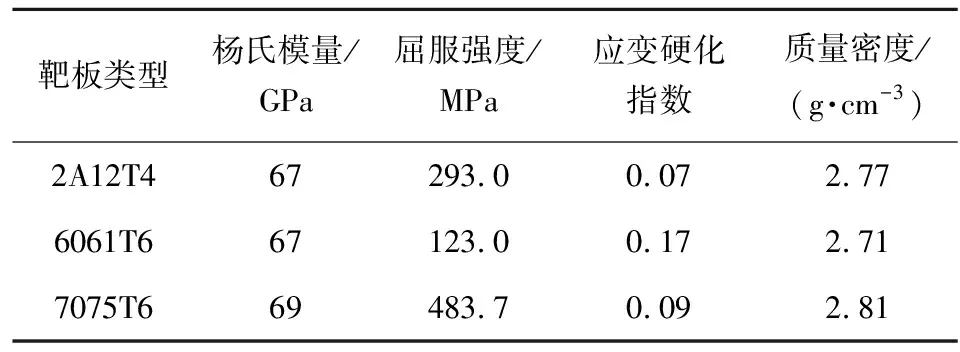
表1 3种铝合金靶板材料的力学性能参数

取图1中的屈服应力点作为塑性段起点,对塑性段的应变硬化指数n进行拟合,得到3种材料的拟合曲线,如图2所示,3种材料的应变硬化指数n见表1所示。将各个参数代入式(6)并积分得到3种铝合金材料的参数I分别为I2A12=4.241,I6061=3.832,I7075=3.800,最终通过式(5)计算得到3种材料的σS为σS,2A12=1.371 GPa,σS,6061=0.941 GPa,σS,7075=2.169 GPa。

图2 3种铝合金材料的应变硬化指数n的拟合

3 弹道试验

为验证上述的穿深方程,开展了上述3种材料的铝合金靶板的末端弹道试验,试验中的发射装置为12.7 mm弹道枪,试验射弹为12.7 mm穿燃弹。如图3所示,在枪口前方3 m处布置光幕测速系统,靶架与枪口的距离约为8 m,靶板材料分别为2A12T4,6061T6和7075T6铝合金,尺寸均约为200 mm×200 mm,将靶板用C型夹固定在靶架上后,按预定的着靶点进行12.7 mm穿燃弹正侵彻试验。

图3 弹道装置示意图

试验射弹的弹芯为硬质钢芯,在侵彻过程中起主要作用,经测量,弹芯的平均质量为29.95 g,平均密度为7.83 g/cm3。弹芯的总长度为52 mm,卵形头部长度为18 mm,弹芯直径为10.8 mm,具体尺寸如图4所示。

图4 弹芯尺寸图

3.1 侵彻试验结果

本次研究进行多发12.7 mm穿燃弹正侵彻试验,得到不同着靶速度下的部分铝合金靶板的侵彻试验结果,如图5所示。从试验结果可以发现,12.7 mm穿燃弹对铝合金靶板的破坏模式为延性扩孔,弹芯在侵彻过程中保持刚性侵彻特征,并且弹芯与靶板材料紧密贴合。在开坑阶段弹丸被甲对弹坑形态造成了一定影响,但在后续的侵彻过程中依旧是弹芯起主导作用,被甲对侵彻深度的影响可以忽略不计,弹坑形态总体上依旧是弹坑底部的尖卵形和弹坑主体部分的圆柱形组成。

图5 不同入射速度下部分铝合金靶板的弹坑截面图

对试验后的弹坑深度进行测量,定义侵彻深度为沿着弹坑的对称轴从靶板迎弹面的光滑平面到弹坑底部尖端的距离[21],得到3种不同强度铝合金靶板的最终侵彻深度与弹丸入射速度的关系,如图6所示。从图6中可以发现,3种铝合金材料的侵彻深度与入射速度的关系较为相似:随着入射速度的增加,侵彻深度的增值越来越大,最终侵彻深度与入射速度近似呈二次指数的函数关系,即侵彻深度与刚性弹丸的动能呈线性正比关系。同时,在弹速范围内(400～900 m/s),靶板材料的强度越高,同一入射速度下的侵彻深度越小(靶板材料强度值见表1所示),说明侵彻过程中弹芯所受阻力受靶板强度的影响较大。

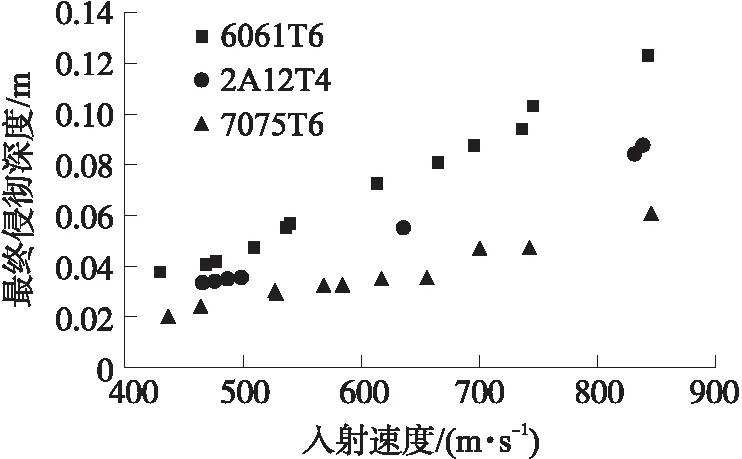
图6 最终侵彻深度与入射速度关系图

3.2 穿深方程验证

将3种铝合金靶板材料和弹芯的各个参数代入式(11)和式(12)后,与试验结果进行对比。图7为3种材料的试验数据与理论模型对比曲线。

图7中,由式(11)的理论模型得到的最终侵彻深度非常接近试验数据,而方程(12)的理论模型与试验结果相比总是偏小。根据2种模型的对比可知,方程(11)的理论模型更为可靠,而通过阻力的积分求解方式推导得到的方程(12)的精确性不足。根据方程(11)的推导过程可知,当弹丸的几何形状和密度确定时,侵彻深度只与刚性弹的入射速度和靶板在平面应变下扩张圆柱腔所需的准静态径向应力σS有关,因此,目标材料的应力-应变数据的精确性是准确预测最终深度的关键。同时,利用方程(11)计算最终侵彻深度时所需要的变量较少,计算过程更为简便。

图7 3种铝合金的侵深试验数据与理论曲线

4 结论

通过弹道试验得到了12.7 mm穿燃弹对3种不同强度铝合金靶板的侵彻深度与速度的关系,基于空腔膨胀理论对延性穿孔过程中的径向应力进行计算,利用动能等效原理推导得到了穿深方程,并与试验结果进行对比,得到如下结论:

①在弹丸几何形状和密度确定的情况下,铝合金靶板在受到刚性卵形弹冲击时的最终侵彻深度可由靶板材料在平面应变下扩张圆柱腔所需的准静态径向应力σS和弹丸的入射速度计算得到。

②将靶板材料变形所做的塑性功等效为弹丸的动能,进而计算最终侵彻深度,此方法是较为可靠的,其准确性得到了试验验证。

③靶板材料的应力-应变数据的可靠性是准确预测最终侵彻深度的关键因素。