基于正交实验的矿用除尘器气流组织设计

2021-07-04肖培杰邹钺沈恒根

建筑热能通风空调 2021年5期

肖培杰邹钺沈恒根

东华大学环境科学与工程学院

0 引言

煤矿作业环境影响工人健康，并且有安全隐患，因此合理的气流组织[1]是非常必要的。CFD[2]具有模拟不同工况的优点，Tecplot 能进行后处理[3]。正交试验是分析多因素试验的方法[4]。本文研究滤料排列方式，进口位置及抽吸压力对气流组织均匀性的影响。利用正交试验方法安排实验，找到因素的重要性排序以及较佳设计方案，为气流组织设计提供依据。

1 模型及试验设计

1.1 正交表设计

影响气流组织的因素有排列方式、进口位置、负压等，为研究三者对气流组织的影响，本文采用正交试验设计方法，每个因素三个水平，增加一个空白列，设计一个L9(34)的正交表[5]。排列的三个水平如图1 所示，各因素位级如表1 所示，试验方案如表2 所示。

表1 实验因素位级表

表2 试验方案表

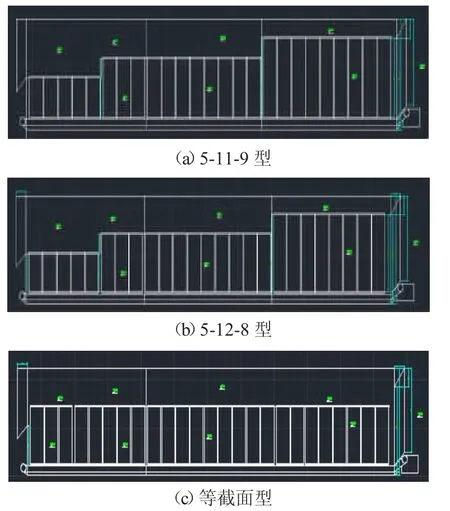
图1 排列水平图

1.2 建模及边界条件

设计的模型尺寸在xyz 方向上分别为：14000 mm、2800 mm、1500 mm，金属滤料的高度分别为：1000 mm、1500 mm、2000 mm，进出口为1250 mm×1400 mm 的矩形，进口距离上表面850 mm，距离右表面100 mm，出气口距离上表面250 mm，距离左表面100 mm。如图2 所示。

图2 除尘器模型

滤料之间的分布如图3 所示，滤料长500 mm，宽30 mm，Z 轴方向滤料之间的距离为30 mm，X 轴方向滤料之间的距离为33 mm。沿出口方向，第一列滤料距离出口壁面200 mm,滤料离两边外壳的距离为75 mm。

图3 滤料内部尺寸设计

考虑到网格的自适应性，对金属烧结板除尘器模型采用非结构化网格进行划分。非结构网格生成方法在生成过程中采用一定的准则进行判断，因而能生成高质量的网格。全局网格尺寸设置中，将尺寸缩放因子设为1，全局最大网格尺寸设为128，将进出口、滤料的最大网格尺寸设为64。采用Tetra/Mixed 的网格类型生成网格[6]。参考市场常见的金属烧结板除尘器，利用ICEM-CFD 建立简化模型。网格数量约309 万，网格质量接近90%大于0.4。

用Ansys fluent 进行模拟计算时，过滤过程采用稳态的基于压力求解器，采用Realizable k-ε 湍流模型，压力速度耦合采用sample 算法，湍流能项，压力耗散率项均采用一阶迎风格式。边界条件为速度入口，压力出口，绝热无滑移壁面，滤料设为多孔跳跃边界条件，其渗透率需要由滤料阻力特性实验得出，由试验知，金属烧结板的渗透率为6.4×109。

1.3 网格独立性验证

按照数值计算的观点，网格大小为零时离散方程才完全与控制方程吻合，但实际上网格大小为零是不实际的。按正常情况来讲，网格加密可以提高计算精度，但是网格密度的加大会增大计算开销，需要更多的CPU 计算时间和内存。此外，计算精度与网格密度也并非成线性关系。当网格密度达到一定程度后，再进一步加密网格，计算误差反而会加大。对该模型采用了4 种密度进行网格划分，对Z=0.8 m 截面上每列滤料的出口速度进行对比，找到一个既能满足计算精度要求，又能满足CPU 性能的网格密度。四种网格数量如下，114 万、308 万、400 万、1700 万。由于1700 万数量太大，运行时间太长，不适合该模型。速度对比如图4 所示。

图4 不同网格数量下的计算结果对比

网格数为144 万时，结果偏差较大，当网格数量增加到309 万、400 万时，两者结果相近，几近于重合，此时在提高网格质量，已没有意义。为了满足计算精度和运行内存的要求，此次模拟选择了309 万的网格数量。

1.4 模拟验证

由于煤矿现场条件的限制，无法测得实验数据。本文以文献[7]建立模型，并设置相同的边界条件，模拟数据和实验数据如图5 所示。

图5 模拟数据与实验数据的对比

由图可知，实验数据和模拟数据两者相差不大。在24 列滤料处速度有所增大，原因可能是在滤料底部形成了涡流，使流速增大，但总体的速度趋势一致。由此可知，本文采用的CFD 方法是符合实际情况的，可以采用模拟的方法来分析气流组织的不均匀性。

2 正交实验结果分析

2.1 不均匀性系数

本文采用不均匀性系数[8]作为气流组织均匀性的评价指标。不均匀性系数为数理统计与概率分析中各离散断面的平均速度的标准差与各断面速度的平均值的比值。不均匀性系数越小，气流组织越均匀，有利于提高滤料的过滤效率，用η 表示，公式如下：

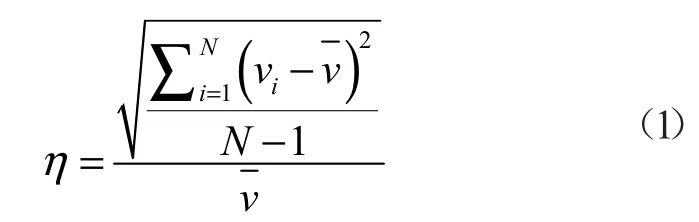
式中：vi为断面速度为平均速度；N 为断面总数。

2.2 方案极差分析

本文沿X 轴方向、在每列滤料的中心切割速度断面，利用Fluent 软件求取断面平均速度。计算得到不同实验下的不均匀系数，如表3 所示。

表3 不同方案下的模拟处理结果

对实验数据进行处理，如表4 所示。其中，Ki表示任一列水平号为i 时，所对应的实验结果之和，ki:ki=Ki/s，s 为任一列上各水平出现的次数，在这里s=3；R 为极差，在任一列上，R=max{K1,K2,K3}，R 越大，因素越重要。

表4 极差分析表

从极差分析表中可以看出，对气流组织的均匀性影响的因素重要性排序依次为进口位置、负压大小、滤料排列。并且方案B3D3A2 更加有利于气流组织的均匀性。

2.3 位级分析

为了研究正交实验中没有选择但有可能是最佳方案的的位级，采用位级分析图来分析[9]，横坐标为各因素位级，纵坐标为该位级下的不均匀系数。由图6 可得，在滤料排列和负压两个因素中，不均匀系数与位级没有直接联系，并且C2 和C3 相等，在进口位置因素中，随着进口位置的下移，不均匀性逐渐减小，趋于平稳。因此，综合考虑认为滤料呈5-12-8 型排列、出口位置在下、负压为-20000 Pa 时气流组织均匀性最好。

图6 位级分析图

2.4 较优方案分析

按照正交实验所找到的较佳方案建立模型并设置边界条件，计算收敛后利用Fluent 进行后处理，计算得到气流组织不均匀系数为0.03，比其它方案更加均匀。由此也可证明正交实验的可行性和有效性。

将计算结果导入Tecplot 中进行后处理，为了能够观察到所有滤料的速度变化，选取Z=0.8 m 处的断面进行截断。图7 和图8 展示了该方案内部的流线图以及速度分布。从流线图可以看出，气流从右侧进气口流入，分别经过高度为2000 mm、1500 mm、1000 mm 的滤料，净化后的气流从上风道由出气口流出。其中在2000 mm 滤料处产生了回流。由速度云图知，气流刚到达进口时速度达到最大值，经过滤料的过滤，速度逐渐减小，降低的幅度非常平缓，在滤料高度变化后速度相差不大。越靠近出口，风机的抽吸作用增强，速度逐渐变大。速度在进出口最大，在滤料中速度相差不大，均匀性较好，有利于滤料的寿命和过滤效率。

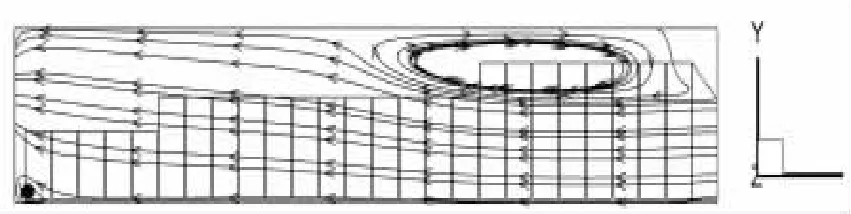
图7 流线图

图8 速度云图

为了能够观察到各列滤料单独的速度变化，每个高度的滤料分别截取某截面进行分析。分别取X=2.865 m、9.261 m、13.492 m 处作为断面，如图9 所示，在靠近进口处滤料速度最大，且分布均匀，在上箱体中速度较小。在1500 mm 高度的滤料中，速度由中心逐渐向外减小，速度与进口处相差不大，上箱体中净化气流由于逐渐增多，速度也渐渐增大。靠近出口处的滤料由于抽吸作用增强，速度呈圆环状，越靠近出口中心处，速度越大。