改进多目标PSO算法优化机器人轨迹跟踪模糊PID控制器

蒋清泽，王宏涛

南京航空航天大学 机电学院，江苏 南京 210016

关节机器人是一个强耦合、高非线性的复杂系统，其轨迹跟踪控制是调整每个关节电机输出的控制扭矩，使得关节角度能够达到期望值[1]。关节机器人轨迹跟踪常用的控制方法主要有基于机器人模型的运动控制方法、PID控制、滑模控制和模糊控制等。其中PID控制技术成熟且易于实现，被广泛应用于机器人轨迹跟踪控制中，但PID算法难以实现非线性系统的高精度控制[2]。因此，有学者提出利用模糊控制无须依靠精确数学模型便能对非线性系统良好逼近的特性，采用模糊PID控制实现机器人轨迹跟踪控制[3]。然而，在实际应用中，控制器输出力矩具有饱和性，如何设计模糊PID控制器使其在有限的输出力矩下达到理想的控制效果是需要专业人员的经验，存在设计不当难以获得最佳效果的不足。均衡评估控制力矩和轨迹跟踪控制效果这2个优化目标可以通过多目标优化算法对模糊PID控制的隶属函数和模糊规则进行寻优调整来实现[4−5]。粒子群算法(PSO)是一种模拟鸟群觅食的启发式算法优化技术，已成功应用于多种优化问题[6]。已有文献证明PSO在单目标优化上具有较快的收敛速度和较好的优化结果，在多目标优化问题上具有较大优势[7]。Mahmoodabadi等[8]用多目标粒子群算法对非线性系统的模糊控制器进行优化，提高了模糊控制器对非线性系统的控制精度；进一步以控制偏差和控制器输出力矩作为2个优化目标，采用多目标粒子群算法对双足机器人轨迹跟踪滑模控制进行了优化，验证了多目标粒子群算法在多目标优化中的优越性[9]。

本文以控制器输出力矩和轨迹跟踪偏差为2个优化目标，实现改进多目标PSO算法优化模糊控制器的隶属函数和模糊规则优化调整。首先设计了机器人轨迹跟踪模糊PID控制器；然后根据模糊PID控制器的多目标优化问题，设计改进多目标PSO算法；最后分别使用改进多目标PSO和基本多目标PSO应用于模糊PID控制的多目标优化问题，对比分析了2种优化算法的优化结果。

1 机器人轨迹跟踪模糊PID控制

机器人轨迹跟踪模糊PID控制系统如图1所示，图中qd和q分别表示六关节机器人各关节期望角度和实际角度；e表示qd与q的偏差,e=qd−q；ec表示偏差变化率，ec=de/dt；图1虚线部分表示模糊控制器，其中e和ec是模糊控制器的输入变量，ΔKP、ΔKI、ΔKD表 示PID调整参数，是模糊控制器的输出变量；τ表示模糊PID控制器的输出控制力矩。控制过程为：首先模糊控制器根据e和ec的值通过模糊化、模糊推理和解模糊得到PID调整参数；然后实现PID控制器3个参数的在线自适应调整，如式(1)，根据式(2)输出控制力矩；最后将控制力矩作用于机器人，得到实际关节角度，并反馈给比较器。

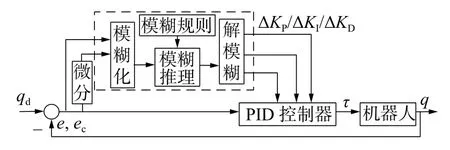
图1 机器人轨迹跟踪模糊PID控制系统

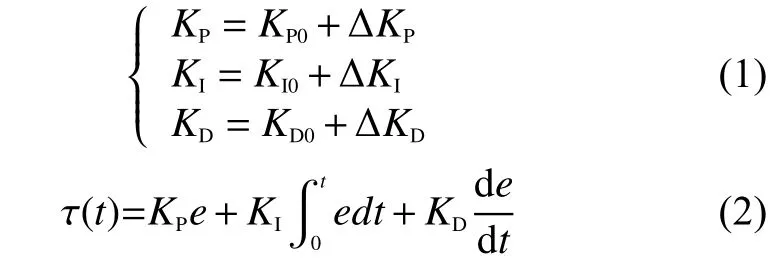
式中：KP0、KI0、KD0为 PID参数的初值；t为时间。

1.1 模糊PID控制器设计

模糊PID控制器中的模糊控制器输入变量偏差e和偏差变化率ec以及输出变量ΔKP、ΔKI、ΔKD的 模糊集个数均设计为7个，其模糊集取为{NL,NM, NS, ZE, PS, PM, PL}，即{负大, 负中, 负小, 零,正小, 正中, 正大}。模糊集隶属函数选取三角形隶属函数，根据隶属函数的特性，某变量所有的模糊集的隶属函数关于Y轴对称，且将某一个三角隶属函数的“左脚”和“右脚”分别设置为相邻左右2个三角隶属函数的顶点横坐标，如图2所示。故在设计每一个变量的隶属函数时，需要确定其论域，以及Y轴某一侧3个参数X1、X2、X3。模糊PID控制器所有变量的隶属函数具体参数如表1所示。

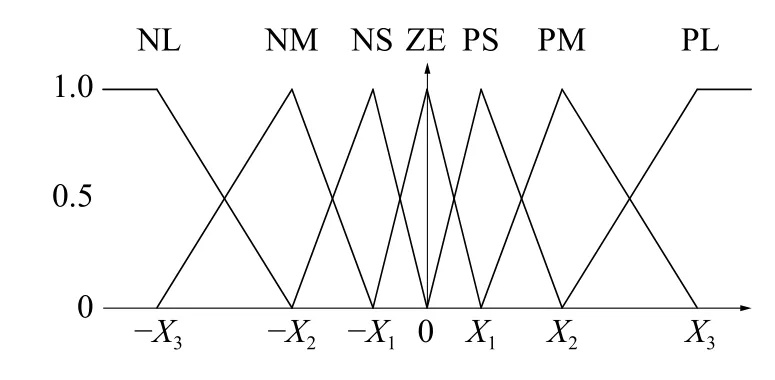
图2 三角形隶属函数

表1 模糊PID控制器输入输出变量隶属函数设计

2个输入变量e和ec的模糊集个数为7，可得输出变量ΔKP、ΔKI、ΔKD的每一个变量所对应的模糊规则均为49条，每条模糊规则的形式为

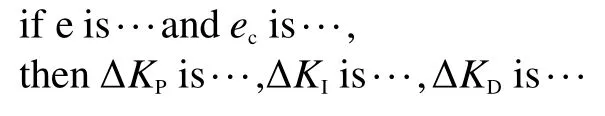
本文设计的ΔKP、ΔKI、ΔKD的 模糊规则如表2所示，数字1～7分别代表NL、NM、NS、ZE、PS、PM、PL。

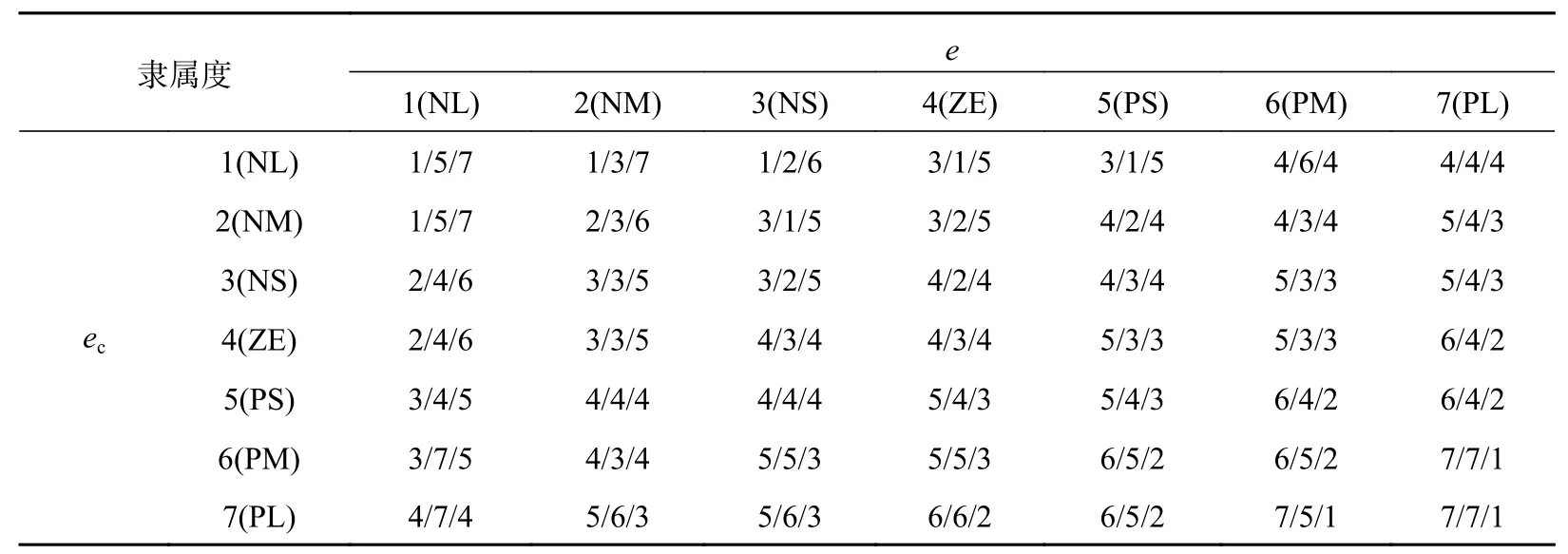
表2 ΔKP/Δ KI/Δ KD的模糊规则表

1.2 机器人动力学模型

忽略关节摩擦和末端负载，六关节机器人动力学方程可以写成如下形式

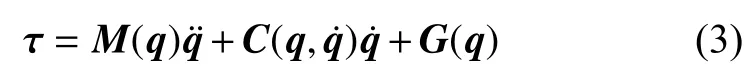
为了对六关节机器人进行仿真，根据上述建立的动力学方程式(3)可计算方程中关节角加速度

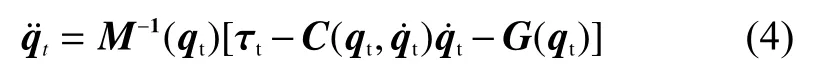
由t时刻的关节角加速度，假设时间步长Δt内不变化, 在初始条件为的情况下,对当前t时刻关节信息qt和进行数值积分, 计算出下一时刻t+Δt的角速度和关节角qt+Δt为

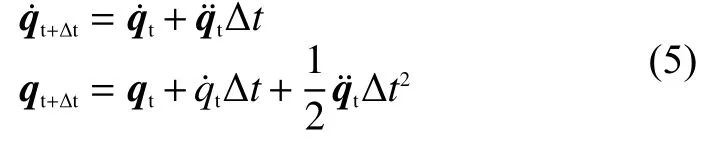
2 模糊PID控制的多目标PSO优化

2.1 模糊PID控制的多目标问题

优化机器人轨迹跟踪模糊PID控制，需要将待优化参数进行编码形成一个决策向量。粒子群算法中的决策向量为某个粒子i的位置向量xi，具体表达为

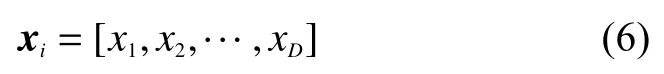
式中：D为优化问题中待优化参数的个数。

PSO优化模糊PID控制的粒子位置向量xi中的元素所代表的参数及参数取值范围如表3所示，其中元素xi,1−xi,15分别表示输入变量e、ec和输出变量ΔKP、ΔKI、ΔKD的隶属函数中心顶点值，每个变量需指定3个中心顶点值，故5个变量需要15个表示模糊PID控制器隶属函数的设计参数；模糊PID控制器总共有3个规则表，每个规则表有49条模糊规则结果需要设计，故需要3×49=147个元素表示，即xi,16−xi,64、xi,65−xi,113、xi,114−xi,162分别表示ΔKP、ΔKI、ΔKD规则的49条模糊规则。故总共需要162位元素基来表示，D=162。

表3 粒子位置向量参数

模糊PID控制有2个优化目标函数，分别与轨迹跟踪偏差和控制器输出力矩有关，如式(7)所示，则目标向量为f=(f1,f2)。

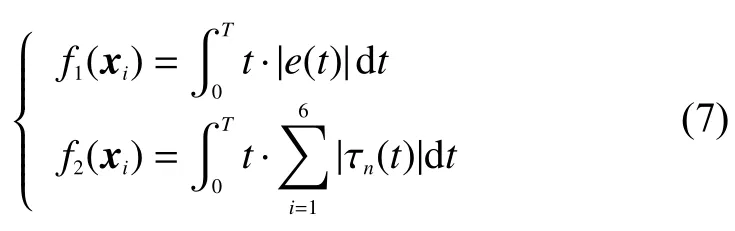
式中：e(t)为t时刻的机器人笛卡尔空间仿真轨迹与期望轨迹的偏差；τn(t)为t时 刻模糊PID控制器作用在第n个 关节的输出力矩；T为运行模糊PID控制器完成一次轨迹跟踪控制仿真的总时间。

模糊PID控制器多目标优化时，最小化控制器输出力矩可能导致轨迹跟踪误差的提高，因此需要在这2个互相冲突的目标中找到权衡的解，而这样的解不唯一。2个粒子的位置向量x1和x2，若对于∀k=1,2，有fk(x1)≤fk(x2)，且对于∃k=1,2有fk(x1)＜fk(x2)，称x1支配x2；否则称x1与x2为非支配关系。多目标优化算法的任务是找到所有不被其他粒子位置向量支配的粒子所对应的目标向量f=(f1,f2)的集合，这些目标向量互为非支配关系，其集合称为非支配解集。

2.2 改进多目标PSO算法

粒子群算法是通过各个粒子位置的不断调整，使得粒子不断向最优位置移动。算法中每个粒子均具有形如[xi,1(k),xi,2(k),···,xi,D(k)]的位置向量xi(k)和形如[vi,1(k),vi,2(k),···,vi,D(k)]的速度向量vi(k)，其中，i=1,2,···,S是粒子在粒子群中的序号，k为迭代次数，S是粒子群的个数。

改进多目标PSO算法优化机器人轨迹跟踪控制模糊PID控制器的流程如图3所示，算法主要步骤如下。

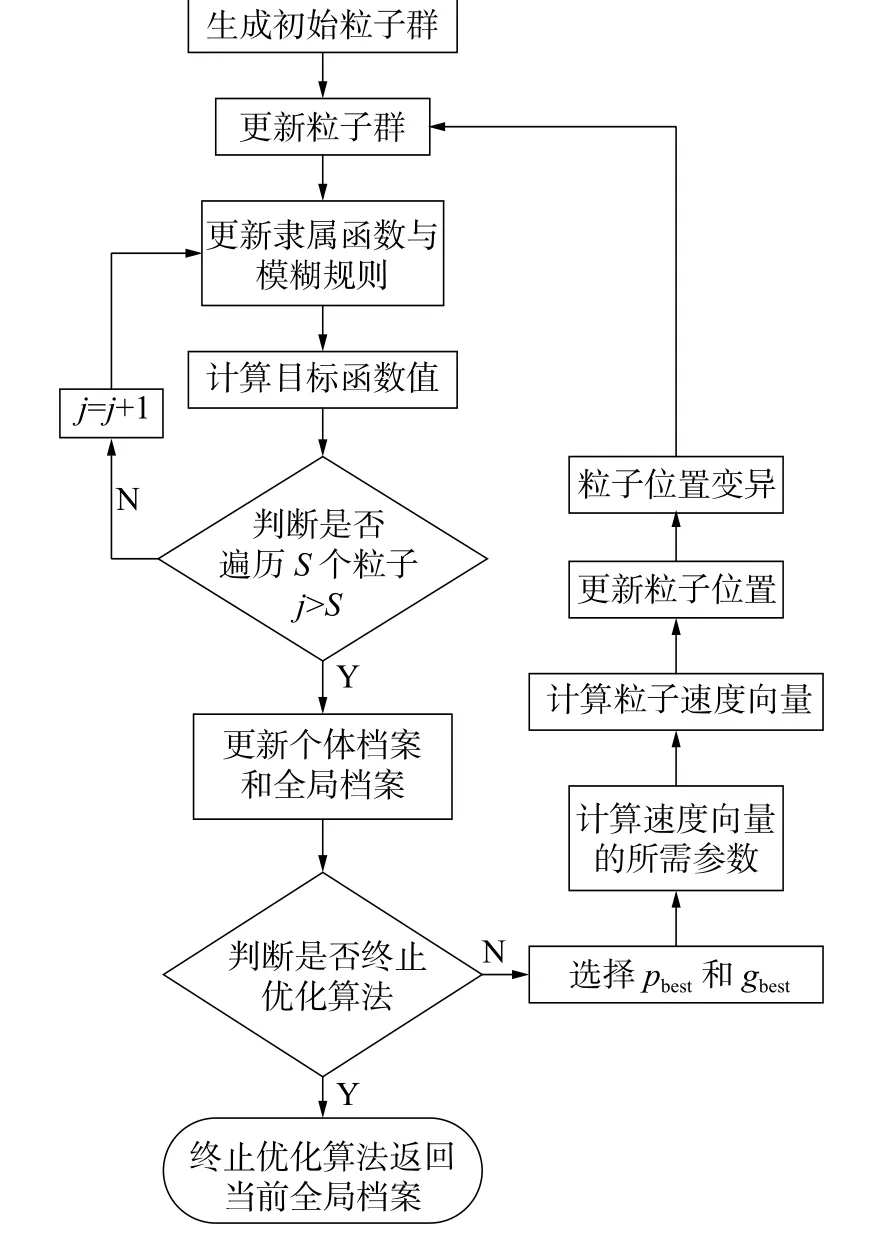
图3 多目标粒子群算法优化模糊PID控制器流程

1）生成初始粒子种群：根据表3，随机生成S个形如[xi,1(0),xi,2(0),···,xi,162(0)]的粒子位置向量xi(0)，且初始种群为{x1(0),x2(0),···,xS(0)}，设置初始种群中所有粒子的速度向量vi(0)=0。

2）更新粒子群：设置第k代粒子群为当前粒子群。

3）更新隶属函数和模糊规则：读取当前粒子群中第j(j=1,2,···,S)个粒子的位置向量，根据编码xi,1(k)−xi,10(k)生成新的输入变量e、ec和输出变量ΔKP、ΔKI、ΔKD的隶属函数，更新隶属函数；根据编码xi,11(k)−xi,63(k)产生新的输出变量ΔKP、ΔKI、ΔKD的 模糊规则，更新模糊规则。

4）计算目标函数值：运行模糊PID控制器完成轨迹跟踪控制仿真，获得仿真控制中t时刻机器人仿真轨迹与期望轨迹的偏差e(t)和各关节控制器的输出ui(t)，根据式(7)计算目标向量f=(f1,f2)。

5）判断是否遍历S个粒子：若粒子数量j不满足j＞S，则j+1，进入步骤3）；若满足j＞S，则进入步骤6）。

6）更新个体档案和全局档案：个体档案和全局档案分别是存储个体最佳位置和全局最优粒子的非支配解集。每个粒子均有自己的个体档案，而全局档案为所有粒子共享。个体档案和全局档案是为步骤8中选择pbest和gbest做准备。若当代粒子群中的粒子与档案中的解集为非支配关系，则将该粒子添加到档案中。

7）判断是否终止优化算法：判断粒子迭代次数k是否达到设定值，若到达最大值，则结束优化算法，返回当前全局档案中的粒子位置向量；若未到达，则进入步骤8）。

8）选择pbest和gbest：需从个体档案和全局档案中的非支配解集中分别选择出来一个确定的值。选择pbest和gbest的具体方法如下，首先对于每一个粒子均被赋予一个值σi，且对于个人档案和全局档案中的每个粒子也被赋予一个值σpi和σgi，目标函数值为f=(f1,f2)的粒子值σ被定义为

然后将个体档案和全局档案中粒子σpi和σgi最接近粒子i的σi的档案成员作为该粒子的向导pbest和gbest。

9）计算速度向量所需参数：速度向量所需参数分别为第k代粒子的惯性权重ω(k)、正加速度系数c1(k)和c2(k)，其具体计算公式如式(9)—式(11)所示

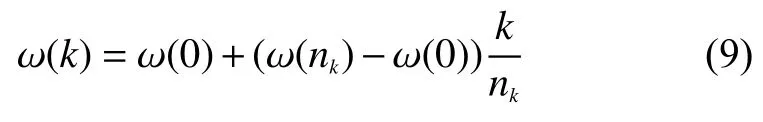
式中：nk为算法设置的最大迭代次数；ω(0)和ω(nk)分别为初始惯性权重和最终惯性权重；ω(k)为第k代的惯性权重，且ω(0)≥ω(nk)。

式中：c1(0)和c1(nk)分别为c1的初值与终值；c2(0)和c2(nk)分别为c2的初值与终值，且c1(0)≥c1(nk)，c2(0)≤c2(nk)。

10）计算粒子速度向量：下一次迭代的速度向量vi(k+1)中第d维速度计算如式(12)所示

式中：Vmax,d为第d维上允许的最大速度；计算如式(13)所示

式中：xi,d(k)和vi,d(k)分别为在k时刻粒子i第d维上的位置和速度，d=1,2,···,D；ω为惯性权重系数；pbesti,d(k)为粒子i从个体档案中选择出来的pbest的第d维，gbestd(k)为在k时刻当前全局档案中选择出来的gbest的第d维；系数r1、r2则为在区间[0,1]上服从均匀分布U(0,1)的随机数。

11）更新粒子位置：根据式(14)更新粒子位置向量xi(k+1)：

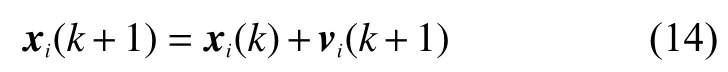
12）粒子位置变异：根据式(15)对新粒子群中的粒子位置进行变异，进入步骤2）。

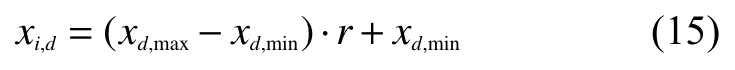
式中：xi,d为粒子i在第d维上的值；xd,max和xd,min分别为粒子在第d维上值的上界与下界；系数r为在区间[0,1]上服从均匀分布U(0,1)的随机数。

3 仿真与结果分析

在机器人轨迹跟踪控制仿真中，设笛卡尔空间的期望轨迹为一段螺旋线，其参数方程如下

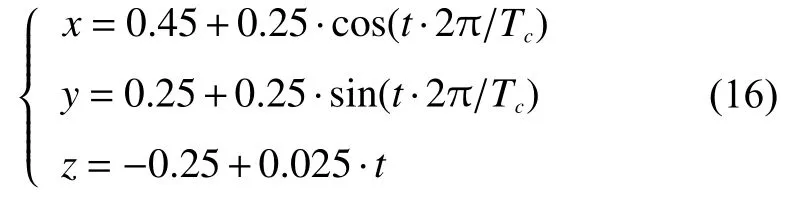
式中：t为时间；Tc为周期时长；x、y、z分别为笛卡尔空间的坐标值。

六关节机器人的D-H参数如表4所示。根据机器人运动学可将笛卡尔空间的期望轨迹转换成机器人关节空间各个关节的期望角度轨迹，如图4所示。本文搭建的机器人轨迹跟踪模糊PID控制的MATLAB仿真系统如图5所示，仿真步长Δt=0.01 s，仿真总时长T=10 s。运用该控制器可以得到各个时刻各关节角度的仿真值和输出力矩值，用于计算优化算法中式(7)的2个目标函数值f1、f2，按照图3的流程图，设置表5的优化算法参数，运行上述设计的控制仿真系统，完成关节机器人轨迹跟踪模糊PID控制器的改进多目标PSO优化。

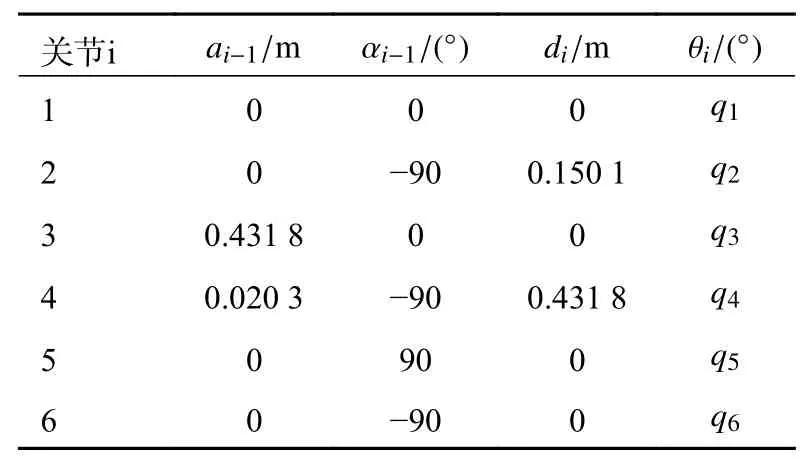
表4 关节机器人D-H参数表

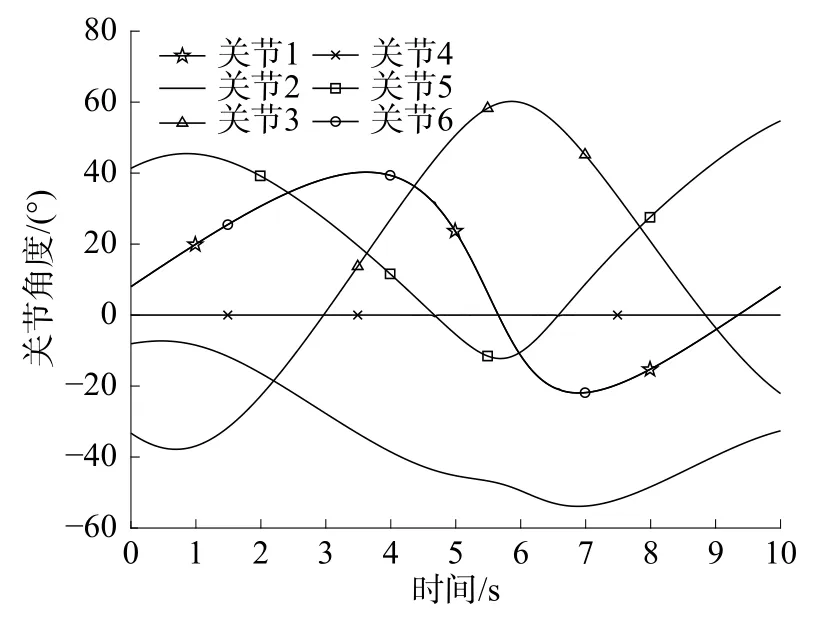
图4 关节空间期望角度轨迹

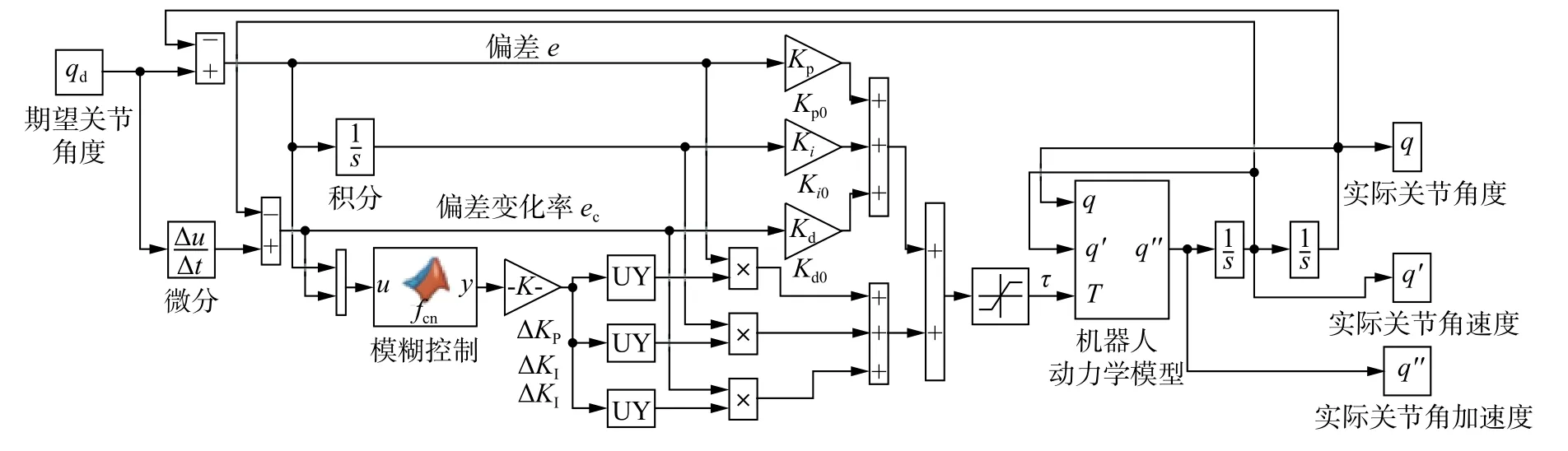
图5 机器人轨迹跟踪模糊PID控制的MATLAB仿真系统

表5 NSGA II优化算法参数

分别采用带精英策略的非支配排序遗传算法(NSGA II)、多目标基本粒子群算法(MOPSO)和改进多目标粒子群算法(Modify MOPSO)进行轨迹跟踪模糊PID控制器优化。NSGA II优化算法的参数设置如表5所示，2种粒子群优化算法的参数设置如表6所示。通过3种优化算法优化后得到的非支配解集如图6所示，解集中各个解的2个目标函数值如表7所示。从图6可以看出，Modify PSO的解集分布较广且均匀，而通过MOPSO得到的部分解集在某一个区域比较集中，且涵盖的范围较小，由NSGA II所得到的解集虽然分布较广，但分布不均匀。采用能够同时评价解集收敛性和多样性的超体积指标来比较3种优化算法获得的非支配解集，超体积越大说明算法综合性能越好。设置超体积的计算参考点为(36.5,14 900)，NSGA II、MOPSO和Modify MOPSO的超体积分别为885.4、3 369.1和7 247.6，可见Modify PSO获得的非支配解集最优。

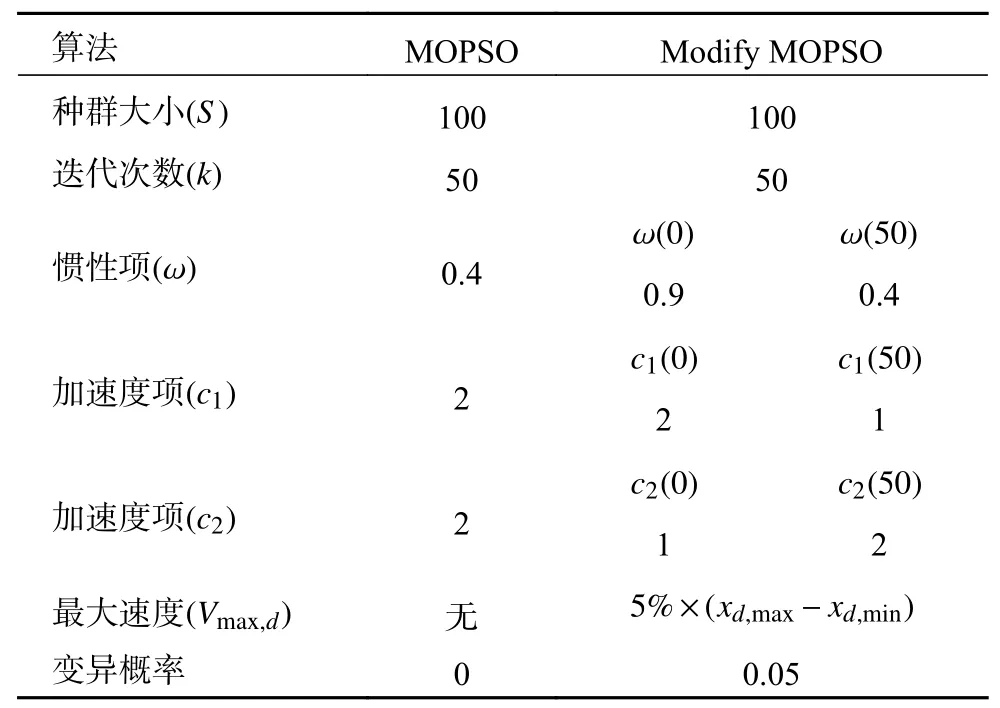
表6 MOPSO和Modify MOPSO优化算法参数

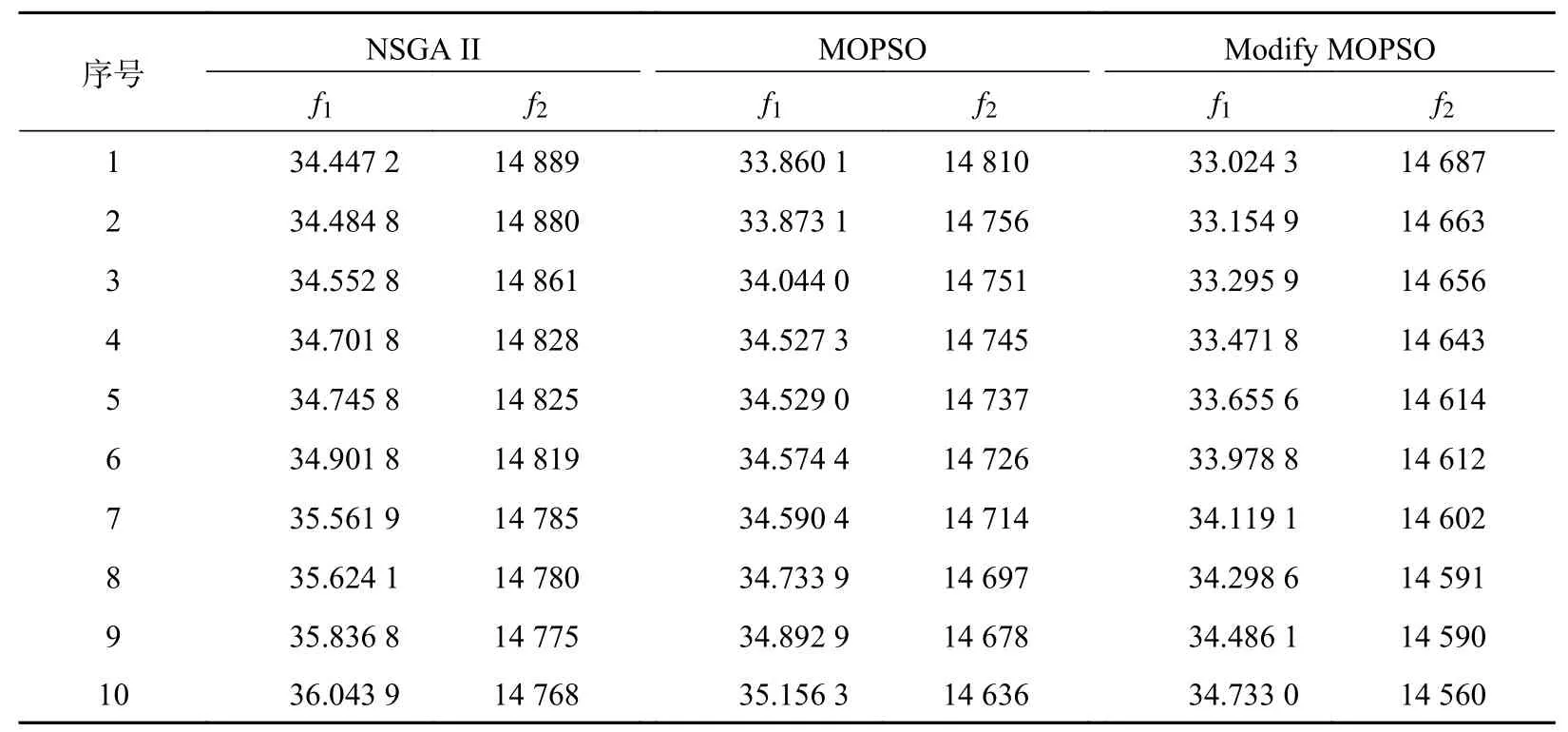
表7 目标函数值

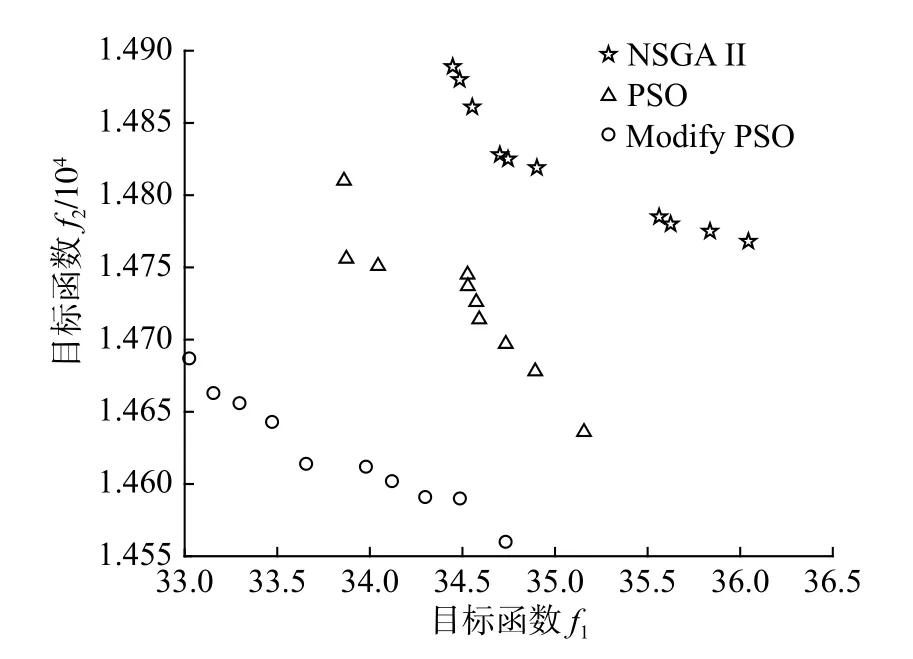
图6 多目标优化结果

综上，改进多目标PSO算法应用于关节机器人轨迹跟踪模糊PID控制器的多目标优化问题，可以得到比基本多目标PSO算法和NSGA II更优的非支配解集，验证了该算法在机器人轨迹跟踪模糊PID控制优化上有效性和优越性。

4 结论

本文设计了一个模糊PID控制器应用于六关节机器人轨迹跟踪控制，以控制器输出力矩和轨迹跟踪偏差为2个优化目标，实现了改进多目标PSO算法优化模糊控制器的隶属函数和模糊规则优化调整。对比改进多目标PSO和基本多目标PSO算法、遗传算法应用于关节机器人轨迹跟踪模糊PID控制器的多目标问题，结果表明，改进PSO获得的非支配解集更好，验证了该算法应用于机器人轨迹跟踪模糊PID控制优化的有效性和优越性。进一步的研究工作是继续探索多目标PSO算法与其他优化算法（如蚁群算法、神经网络算法等）实现机器人轨迹跟踪控制器优化的效果，进行对比分析。