考虑腹板剪切变形的波形钢腹板组合梁翼缘有效宽度计算方法

吴启明，董桔灿

（深圳市市政设计研究院有限公司 深圳518029）

0 引言

与传统混凝土梁类似，波形钢腹板组合梁也存在剪力滞效应。工程设计时，通常采用翼缘有效宽度来考虑梁式结构的剪力滞效应，各国规范针对混凝土梁、钢梁、组合梁均有相应的规定，但对于波形钢腹板组合梁，至今仍缺乏计算依据。另一方面波形钢腹板组合梁在国内已有相当的应用［1-2］，因此有必要对波形钢腹板组合梁剪力滞和翼缘有效宽度进行深入研究。

吴文清［3］最早于2002 对波形钢腹板组合梁的剪力滞效应问题进行了比较系统的研究，提出了基于能量变分法的等截面梁剪力滞效应微分方程；李兴坤等人［4］首次采用二次项与三次项拟合来描述箱梁翼板的纵向位移函数，推导波形钢腹板箱梁剪力滞效应计算公式。周勇超等人［5］研究了变截面波形钢腹板组合梁剪力滞翘曲位移函数模式，推导了翼缘板的纵向位移幅值函数的计算公式。吴启明等人［6］提出了一种通过翼缘板应力分布计算的变厚度翼缘板有效宽度的定义式，初步探讨了各国规范关于翼缘有效宽度规定的适用性问题。姜瑞娟等人［7］通过引入3个不同的广义位移函数，以模拟截面各部分的不同位移形式，基于能量变分法提出了变高度波形钢腹板组合梁剪力滞效应的理论分析方法。此外蔺鹏臻等人［8-13］也进行了相关研究。可见，目前波形钢腹板组合梁剪力滞效应或翼缘有效宽度的研究已有一定的基础。

波形钢腹板组合梁由于腹板剪切刚度低，受弯时剪切变形较为显著，挠度计算时应考虑其影响，这点已基本上成为业内共识，苏俭等人［14-17］也进行了这方面的研究。但腹板剪切变形对剪力滞效应有何影响，该如何计算，需要进一步研究。李夏元等人［18］基于铁木辛柯梁理论，建立了薄壁箱梁剪力滞效应的能量变分方程，但波形钢腹板组合梁与一般薄壁构件存在力学特性上的差异，铁木辛柯梁理论是否适用于波形钢腹板组合梁是个问题。至少周朋［19］的研究结果表明，当梁跨较小时，按铁木辛柯梁理论计算的波形钢腹板组合梁挠度大于三维有限元分析的结果。

针对上述问题，本研究在姜瑞娟等人［7］提出的波形钢腹板组合梁剪力滞效应分析方法的基础上，进一步推广到变高度梁，并通过使用不同的内力计算方法，以考虑剪切变形的影响，以一等高连续梁和一变高度连续梁为对象，研究剪切变形对波形钢腹板组合梁翼缘有效宽度的影响，并对用于波形钢腹板组合梁翼缘有效宽度计算，并考虑剪切变形影响的内力计算方法进行评估。

1 剪力滞效应分析方法

将文献［7］提出的波形钢腹板组合梁剪力滞效应分析方法推广至变高度梁后，组合梁的剪力滞效应微分方程为：

式中：I为整个截面的惯性矩，I=I1+I2+I3+Iw；I1、I2、I3、Iw分别为悬臂板、箱内顶板、底板、腹板绕组合截面中性轴的惯性矩；U1、U2、U3为悬臂板、箱内顶板、底板翘曲位移幅值函数；M（x）、Q（x）分别为梁的弯矩和剪力；w 为组合梁的挠度；E为混凝土的弹性模量。式⑴为边界条件，当翼缘板固接时，Ui=0；当翼缘板非固接时

式中：z为应力计算点至截面中性轴的距离，上为正、下为负；y为应力计算点至腹板边缘的距离；i=1，2，3分别表示悬臂板、箱内顶板、底板。图1为组合梁的剪力滞效应示意，图1中σ xi为每块翼缘板的应力分布；bi为每块翼缘板的宽度。

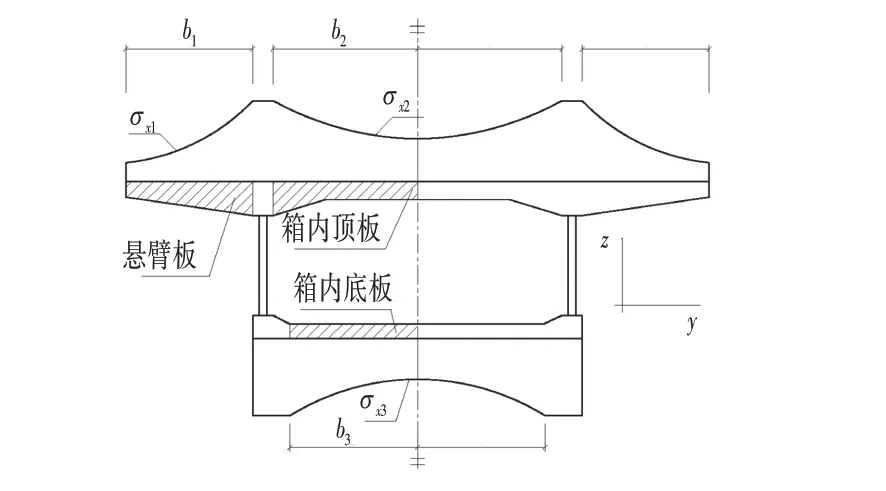
图1 波形钢腹板组合梁剪力滞效应Fig.1 Shear-lag Effect of Composite Girders with Corrugated Steel Webs

为考虑剪切变形的影响，采用不同的梁理论求解内力，然后将内力结果代入式⑴、式⑵求解方程后，根据式⑶可得到组合梁的应力分布，最后使用文献［6］中的定义方法可计算翼缘有效宽度系数ρi，i=1，2，3，分别表示悬臂板、箱内顶板、底板的翼缘有效宽度系数。

2 算例分析

2.1 （30+50+30）m等高度连续梁

采用单箱单室截面，梁宽16.5 m，梁高2.5 m。翼缘板采用C50混凝土，材料弹性模量3.45×104MPa，泊松比0.2；钢腹板型号为1000 型，厚度9 mm，采用Q345C 钢材，材料弹性模量为2.06×105MPa，泊松比为0.31。截面细部构造如图2 所示，从结构的跨径和截面几何参数可以看出，该结构具有较大的宽跨比，剪力滞效应显著。

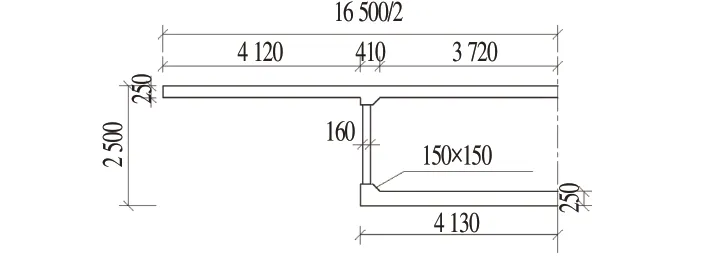
图2 1/2截面细部构造Fig.2 Details of the Half Cross-section （mm）

为研究剪切变形对剪力滞效应的影响以及不同梁理论的适用性，采用欧拉梁理论、铁木辛柯梁理论、实体有限元法3 种方法计算组合梁的内力M（x）、Q（x），其中欧拉梁理论不考虑剪切变形影响，铁木辛柯梁理论和实体有限元法可考虑剪切变形影响，并且实体有限元法的内力结果最准确。3种方法对应的工况分别为：工况1、工况2、工况3。与此同时，采用实体有限元分析得到的应力计算翼缘有效宽度进行验证，为工况4。ANSYS 实体有限元模型如图3 所示，模型中翼缘板支点横隔板采用SOLID95、SOLID92单元模拟，跨间横隔板、波形钢腹板采用SHELL63单元模拟。

图3 实体有限元模型Fig.3 Solid Finite Element Model

为比较不同方法的优劣和剔除无关紧要位置的奇异数据，引入权重系数W进行数据处理和分析。权重系数的确定方法为：权重系数为0～1，其大小和弯矩绝对值正相关并按弯矩区进行划分，弯矩区为以零弯矩位置划分的同号弯矩区段；每个弯矩区中，弯矩绝对值最大的位置权重系数最大，其余位置根据弯矩绝对值大小按指数衰减；每个弯矩区的最大权重系数，通过弯矩区之间的最大弯矩绝对值的比值确定。权重系数具体计算公式如下：

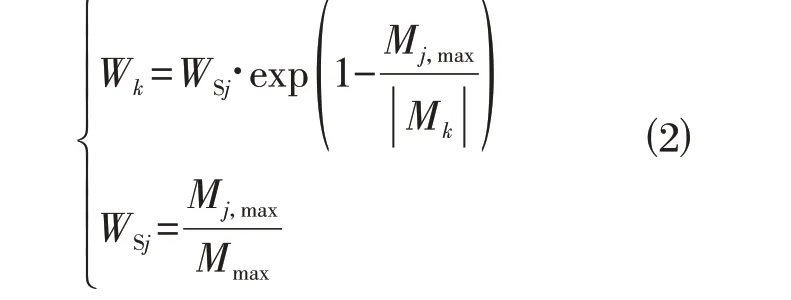
式中：j为弯矩区；k为位置；Wk为k位置处的权重系数；WSj为j弯矩区的最大权重系数；Mj，max为j弯矩区中所有位置弯矩绝对值的最大值；Mmax为所有位置弯矩绝对值的最大值。

组合梁在均布荷载作用下的的弯矩和权重系数分布如图4所示。

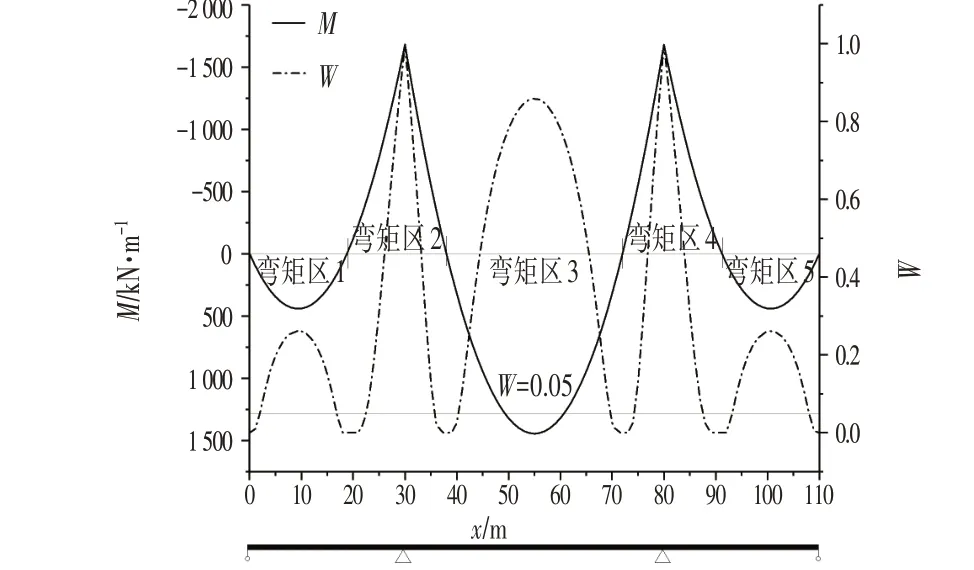
图4 组合梁在均布荷载作用下的的弯矩和权重系数分布Fig.4 Contribution of Bending Moment and Weight on the Composite Beam under Uniform Load

组合梁10kN/m均布荷载作用下Wj，i＞0.5 位 置 处 的翼缘有效宽度系数ρ1、ρ2、ρ3对比结果如图5 所示。由图5 可知，3 种内力解得到的翼缘有效宽度结果均与实体有限元验证结果吻合较好。

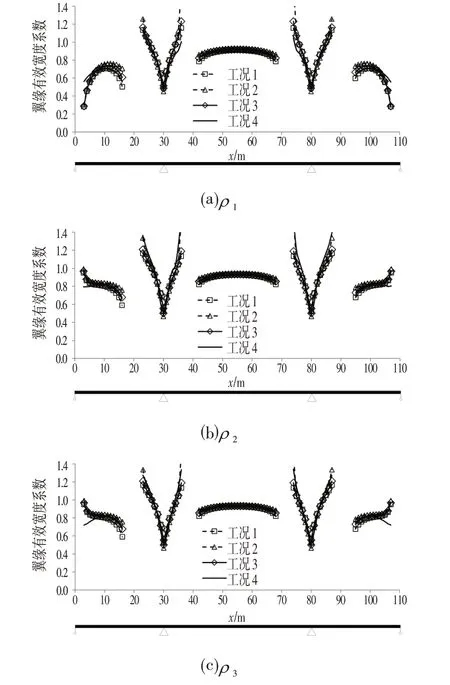
图5 组合梁翼缘有效宽度系数对比Fig.5 Comparison of the Effective Flange Width Coefficients of Composite Beam

关键位置：边跨最大弯矩位置、中支点、中跨跨中的翼缘有效宽度系数对比结果如表1 所示，由表1 中数据可知：对于边跨最大弯矩位置和中跨跨中，精度从高到低的顺序依次为欧拉梁内力解、实体有限元内力解、铁木辛柯梁内力解，其误差分别3%以内、5%以内、10%以内；对于中支点，总体而言精度从高到低的顺序依次为实体有限元内力解、铁木辛柯梁内力解、欧拉梁内力解，其中实体有限元内力解的误差大致为5%，铁木辛柯梁内力解、欧拉梁内力解的误差为10%以内。

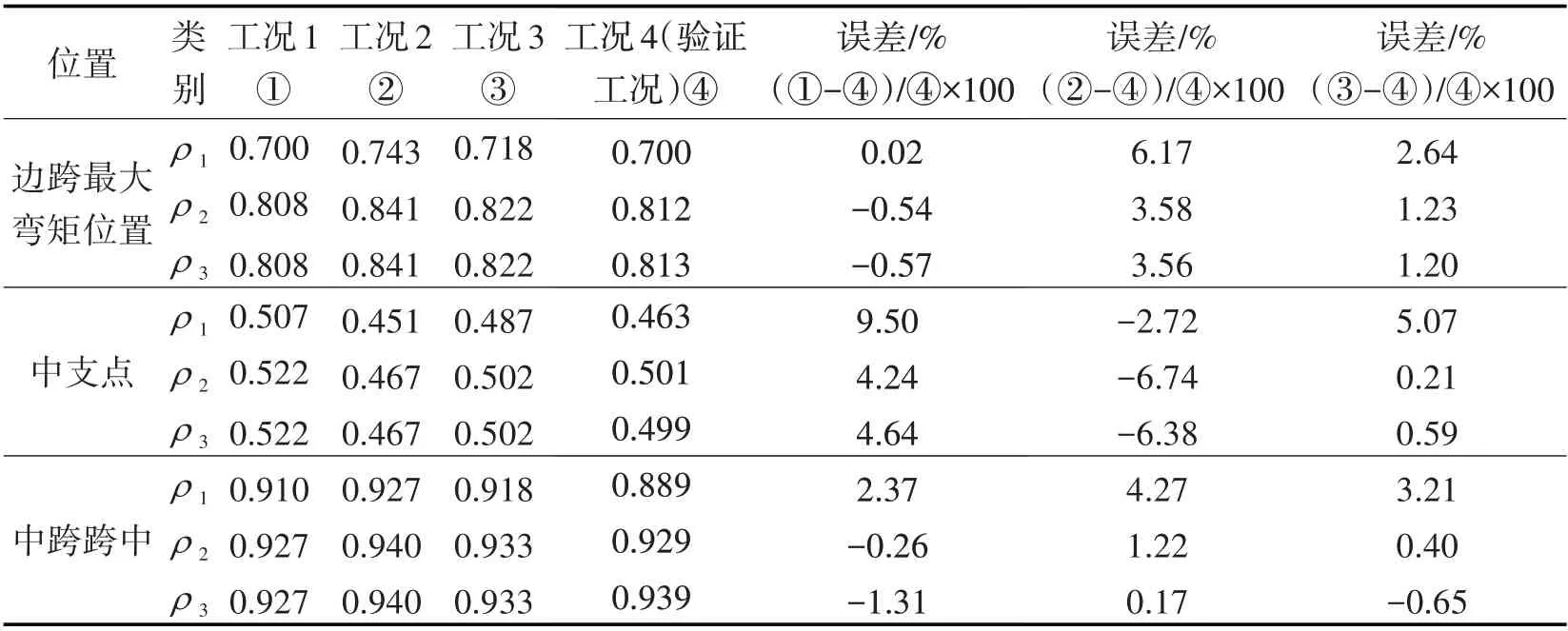
表1 组合梁关键位置翼缘有效宽度系数对比Tab.1 Comparison of the Effective Flange Width Coefficients on Critical Position of Composite Beam

由表1可知采用实体有限元内力解的翼缘有效宽度系数结果比采用铁木辛柯梁内力解的结果精度高，但却无法直接比较2 种内力计算方法的优劣。为此，引入量化指标∆ρ来衡量不同内力计算方法下翼缘有效宽度系数结果的精度。量化指标△ρ反映计算结果的累计误差，同时考虑不同位置的重要性，从结构安全的角度来看，弯矩大的位置往往控制设计，因此某位置弯矩越大越具重要性，而式⑵计算的权重系数W可表征这种重要性。量化指标△ρ按下式计算：

3种内力计算方法下的翼缘有效宽度系数结果精度对比如表2所示，由表2可知，采用实体有限元内力解的翼缘有效宽度系数结果精度最高，其次为采用欧拉梁内力解，最后为铁木辛柯梁内力解。

表2 翼缘有效宽度系数计算精度对比Tab.2 Comparison of the Accuracy of the Effective Flange Width Coefficients

2.2 （88+156+88）m变高度连续梁

采用单箱单室截面，梁宽16.25 m，梁高3.5～8.3 m为1.6 次抛物线。翼缘板采用C60 混凝土，材料弹性模量3.5×104MPa，泊松比0.2；钢腹板型号为1600 型，厚度12～34 mm，采用Q345C 钢材，材料弹性模量为2.06×105MPa，泊松比0.31。截面细部构造如图6所示，ANSYS 局部实体有限元模型如图7 所示，模型中翼缘板、横隔板采用SOLID95、SOLID92 单元模拟，波形钢腹板采用SHELL63 单元模拟，由于结构对称，为节约计算资源，只建了一边跨和1/2中跨模型。

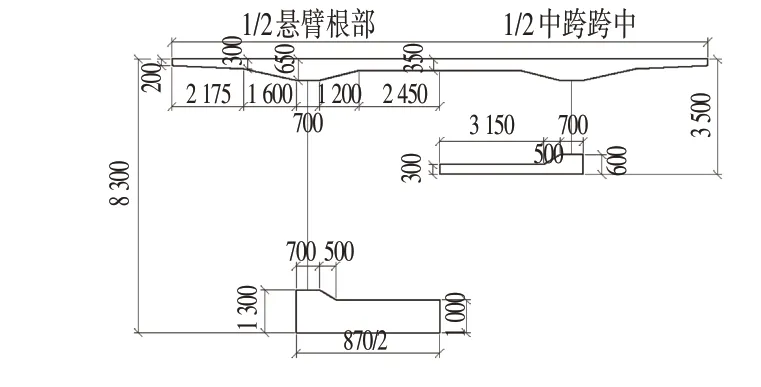
图6 截面细部构造Fig.6 Details of the Cross-section（mm）

图7 局部实体有限元模型Fig.7 Partial Solid Finite Element Model

均布荷载作用下连续梁均布荷载作用下Wj，i＞0.5 位置处的翼缘有效宽度系数ρ1、ρ2、ρ3对比结果如图8 所示，此外连续梁中支点节段由于为体积较大的实心块，构造复杂，应力扰动明显，图8中未给出中支点区域6 m 范围内的数据。图8 中数据表明，欧拉梁内力解的翼缘有效宽度系数结果与铁木辛柯梁内力解的翼缘有效宽度系数结果，均与实体有限元验证结果吻合较好，由此可见，剪切变形对变高度梁剪力滞效应影响不大。

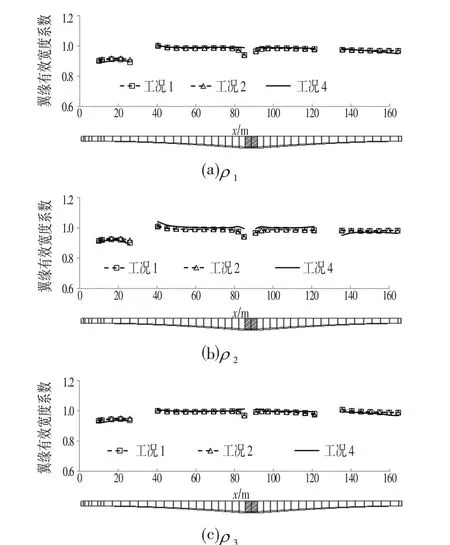
图8 连续梁翼缘有效宽度系数对比Fig.8 Comparison of the Effective Flange Width Coefficients of Continuous Beam

为比较具体数值结果，选取边跨最大弯矩位置A（x=10.0 m）、边跨负弯矩位置B（x=76.7 m）、中跨负弯矩位置C（x=99.3 m）及中跨跨中附近D（x=164.4 m）为对象。A～D位置的翼缘有效宽度系数对比结果如表3所示，由表3数据可知，欧拉梁内力解的翼缘有效宽度系数结果与铁木辛柯梁内力解的翼缘有效宽度系数结果，均与实体有限元验证结果吻合较好，误差在3%以内。

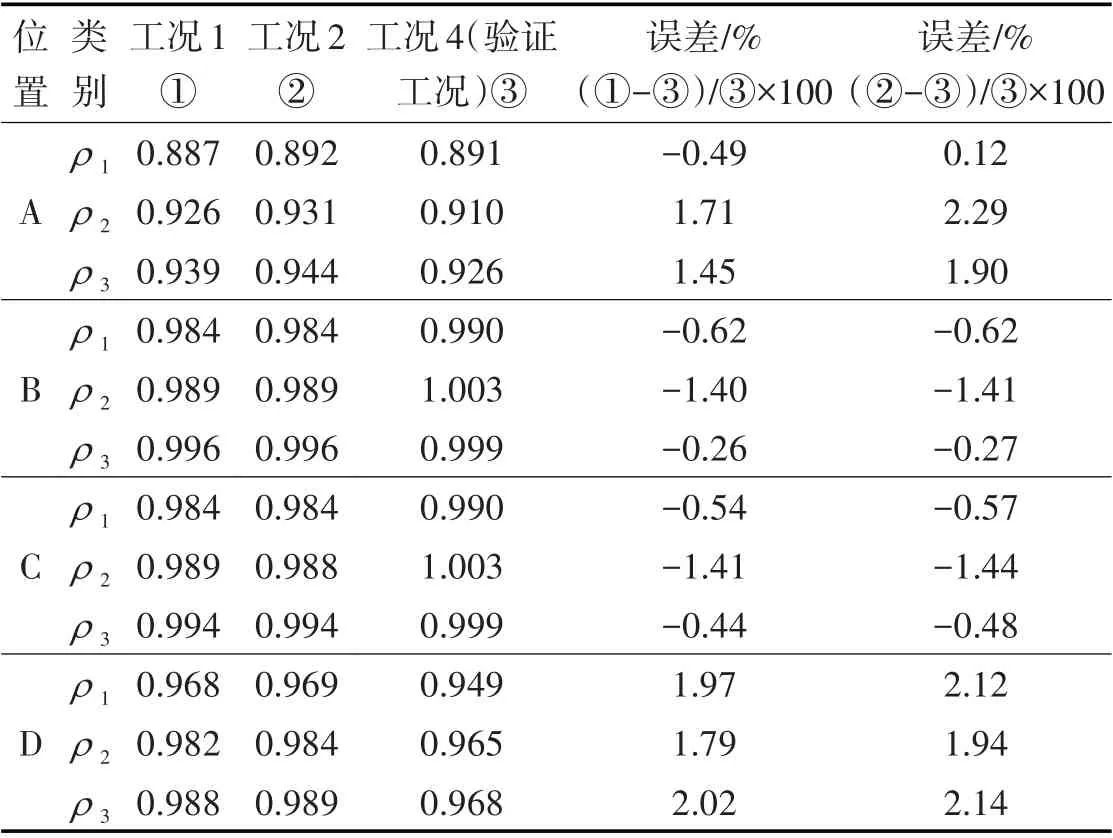
表3 连续梁关键位置翼缘有效宽度系数对比Tab.3 Comparison of the Effective Flange Width Coefficients on Critical Position of Continuous Beam

3 结论

⑴将等高度波形钢腹板组合梁剪力滞效应分析方法推广至变高度梁，借助该分析方法，以一等高度连续梁为对象计算了欧拉梁理论、铁木辛柯梁理论、实体有限元3种不同内力解情况下的翼缘有效宽度系数，并与有限元法验证结果进行了对比。结果表明，采用实体有限元内力解时精度最高，其次为采用欧拉梁内力解，铁木辛柯梁内力解精度最低。

⑵实体有限元内力解的误差大致为5%以内，表明本文推广至变高度的波形钢腹板组合梁剪力滞效应分析方法有较高的准确性。

⑶以一变高度连续梁为对象，研究了欧拉梁理论与铁木辛柯梁理论内力解情况下的翼缘有效宽度系数，结果表明，2 种内力解得到的结果均有很高的精度，因此腹板剪切变形对变高度波形钢腹板组合梁剪力滞效应影响不大。