多自由度非线性悬架系统混沌特性
2021-07-03叶宇翔张翔
叶宇翔,张翔
(200093 上海市 上海理工大学 机械工程学院)
0 引言
悬架系统作为缓冲和吸收振动的主要构件,其性能的好坏会严重影响到汽车的平顺性[1]。悬架系统具有较强的非线性,汽车悬架的非线性因素一般集中在悬架弹簧、阻尼及轮胎上[2],而非线性因素在特定的激励幅值和激励频率下会产生巨大的变化,进而对非线性系统运动学特征产生较大的影响。Wu[3]等建立了包括驾驶员模型在内的整车八自由度模型,在正弦路面激励下,通过分析非线性系统的庞加莱(Poincaré)截面和最大Lyapunov 指数,证明非线性系统存在混沌现象。
本文推导出整车七自由度动力学微分方程,考虑悬架弹簧、阻尼的非线性,利用MATLAB/Simulink 建立仿真模型,在正弦路面激励下,用4 阶Runge-Kutta 法对整车模型进行仿真分析[5]。通过分析庞加莱(Poincaré)截面和Lyapunov指数,发现悬架系统的运动状态随着路面的变化,在周期状态、倍周期状态和混沌状态之间多次变迁。
1 整车非线性系统搭建
如图1 所示,模型考虑了车身的垂向振动、俯仰、侧倾3 个自由度,4 个车轮垂向的4 个自由度[4],建立整车七自由度数学模型。
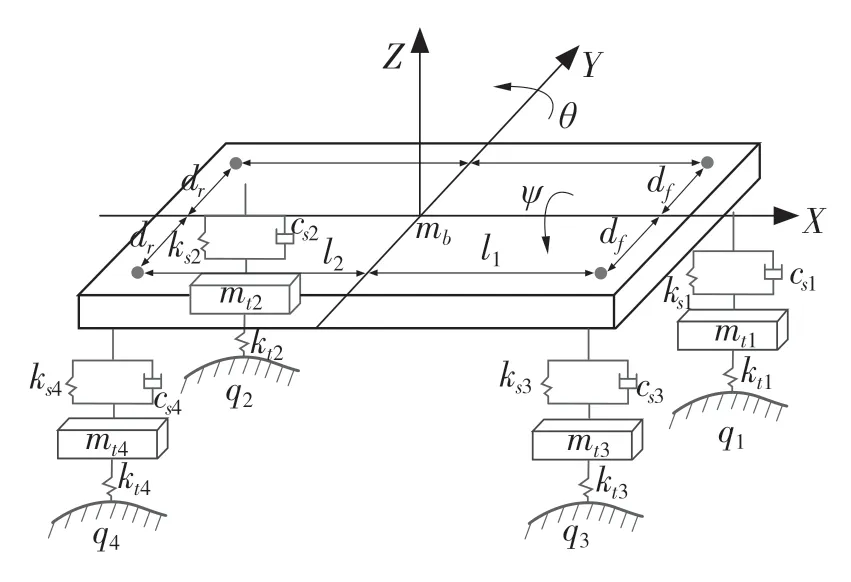
图1 七自由度整车模型Fig.1 7-DOF vehicle model
1.1 非线性悬架系统搭建
悬架系统的非线性弹簧力和阻尼力表示为

式中:ki1,ki2,ki3——悬架系统刚度系数;——悬架系统阻尼系数;——悬架拉伸行程阻尼系数;——悬架压缩行程阻尼系数;ΔZsi——悬架系统的动行程;——动行程变化的相对速度。
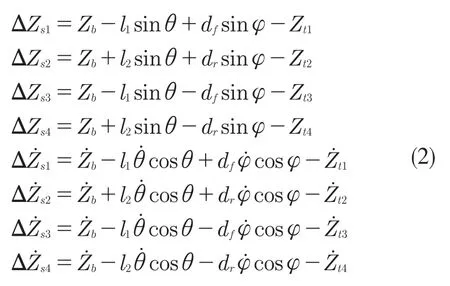
式中:df——前轮轮距的一半;dr——后轮轮距的一半;l1——前轴至车辆质心的距离;l2——后轴至车辆质心的距离;Zb——车身的垂向位移;θ——车身俯仰角;φ——车身侧倾角。
将车轮进行线性化处理,作用在车轮上的地面反作用力为

式中:kti——车轮刚度;qi——车轮接地面的垂向位移。Zti——轮心处的垂向位移。
1.2 汽车整车数学模型
根据牛顿运动定律,建立整车运动学方程:
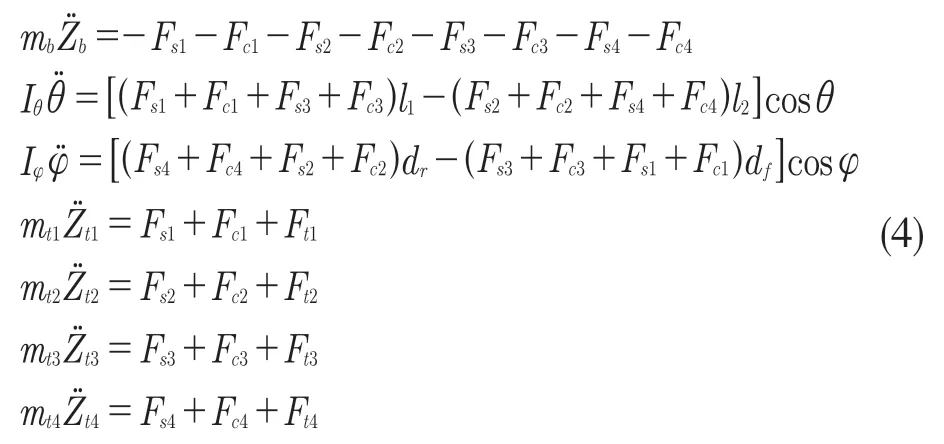
式中:mb——车身质量;m1——左前轮质量;m2——左后轮质量;m3——右前轮质量;m4——右后轮质量;Iθ——车身俯仰转动惯量;Iφ——车身侧倾转动惯量。
1.3 路面激励
采用正弦路面激励,只考虑前后车轮的相角延迟,不考虑路面激励幅值的影响,公式如下:
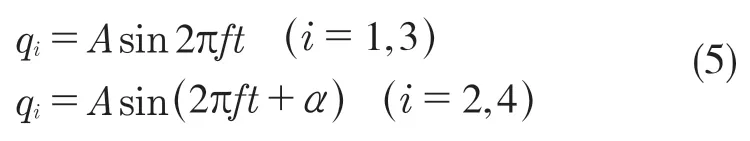
式中:A——路面激励幅值;f ——路面激励频率;α——前后轮激励相角延迟。
2 系统的仿真模型
2.1 车辆在垂向激励下的混沌分析
在不同路面激励频率下,非线性因素会产生巨大的变化,因而影响车身垂向位移和车轮垂向位移。激励振幅为0.005 m,激励频率1~20 Hz,采用龙格库塔法对模型进行求解[6]。考虑相角延迟为α=49π/180,将不同频率下的车辆悬架特性参数输入Simulink 仿真模型中,以激励频率、庞加莱(Poincaré)截面为横纵坐标,绘制车身垂向位移分岔图、车轮垂向位移分岔图,如图2 所示。
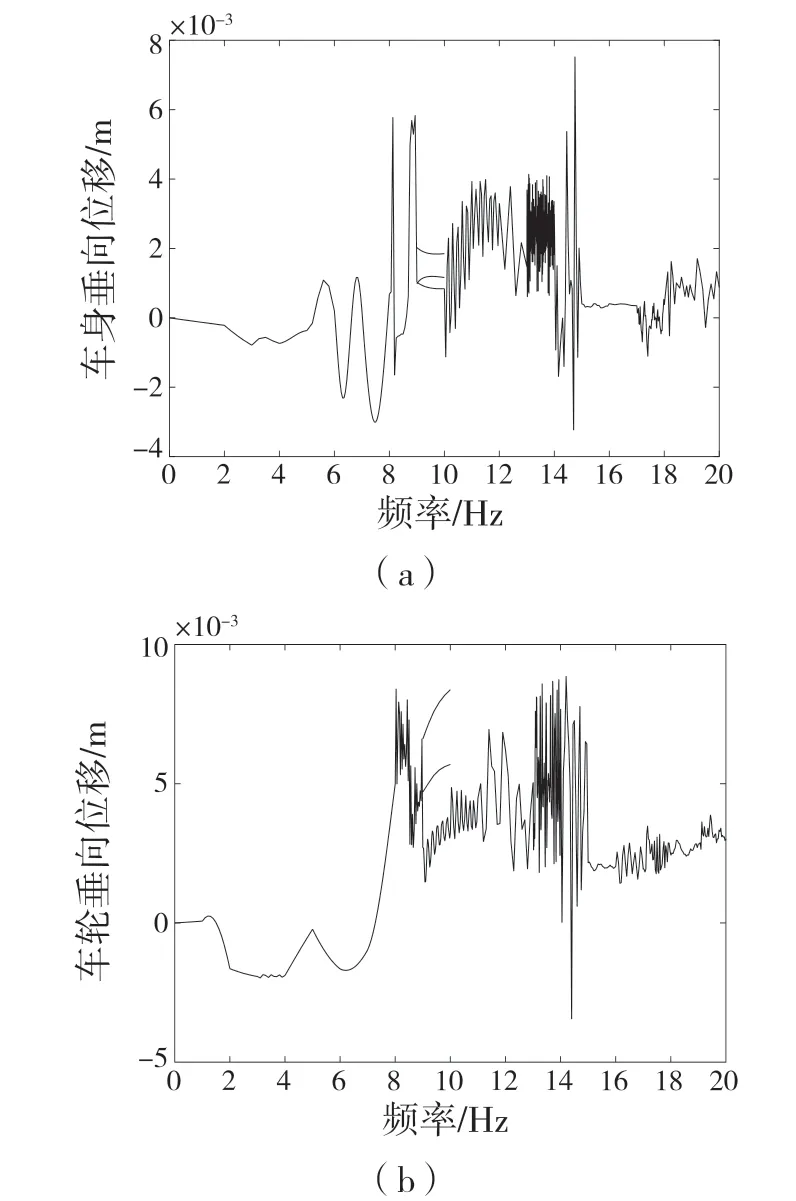
图2 车辆模型频率分岔图Fig.2 Vehicle model frequency bifurcation diagram
从图2 中可以看出,当f=9 Hz 时,出现分形现象,系统运动状态出现突变,可能出现混沌运动;当f=11~14 Hz 时,分岔图中庞加莱(Poincaré)截面点数变多,可能是混沌状态;当f=15~17 Hz 时,庞加莱(Poincaré)截面点数减少,系统趋于稳定,可能再次进入周期运动。分析结果表明,路面激励频率不同会导致悬架系统的运动状态发生改变。根据上述非线性系统仿真分析,选取5,9,14,17 Hz 的路面激励频率进行深入研究。
2.2 混沌现象分析
混沌运动对初值较为敏感,易产生随机性的非周期运动,且不可预测。选取5,9,14,17 Hz激励频率下,分析车身垂向位移的时域信号、相轨迹、庞加莱(Poincaré)截面、功率谱和最大Lyapunov 指数。
(1)第1 组(f=5 Hz)
由图3 所示,时间历程图稳定具有较强规律性,相轨迹表现为大量圆环叠加,庞加莱(Poincaré)截面形成封闭的圆环,此时最大Lyapunov 指数为-0.598 2。由混沌识别方法可知,该七自由度车辆系统呈现周期运动。
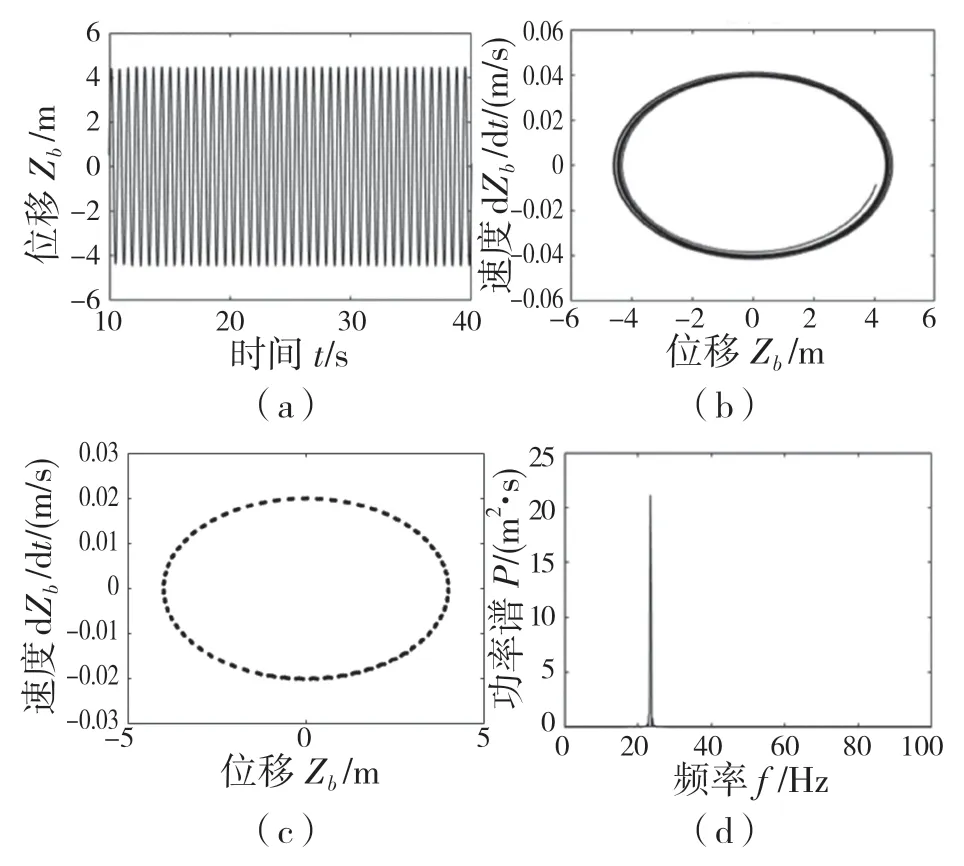
图3 f=5 Hz 时系统各参数曲线和图谱Fig.3 System parameter curve and graph (f=5 Hz)
(2)第2 组(f=9 Hz)
由图4 所示,时间历程较稳定但开始出现不规律变化,相轨迹表现为大量圆环叠加,庞加莱(Poincaré)截面形成多个封闭的圆环,功率谱开始出现连续趋势但有明显的尖峰,此时最大Lyapunov 指数为0。由混沌识别方法可知,该七自由度车辆系统呈现倍周期运动。
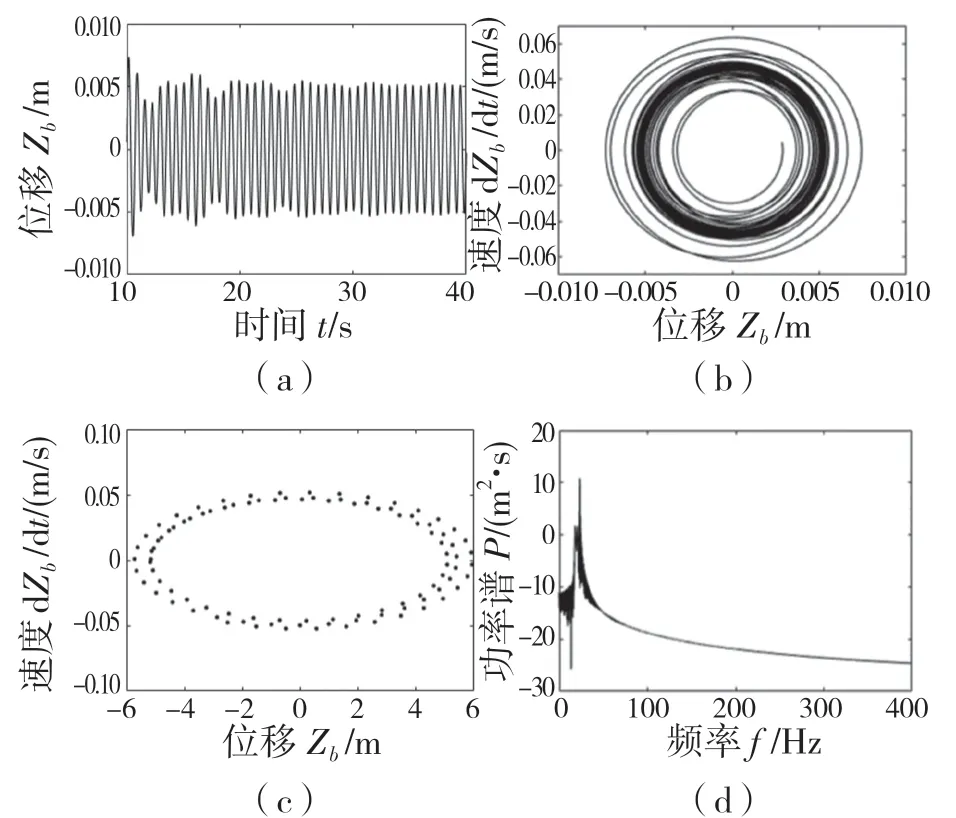
图4 f=9 Hz 时系统各参数曲线和图谱Fig.4 System parameter curve and graph (f=9 Hz)
(3)第3 组(f=14 Hz)
由图5 所示,时间历程图不规律,相轨迹不重复且杂乱无章,庞加莱(Poincaré)截面出现大量密集的点,功率谱呈现出连续现象,此时最大Lyapunov指数为0.534 6。由混沌识别方法可知,该七自由度车辆系统处于混沌运动状态。
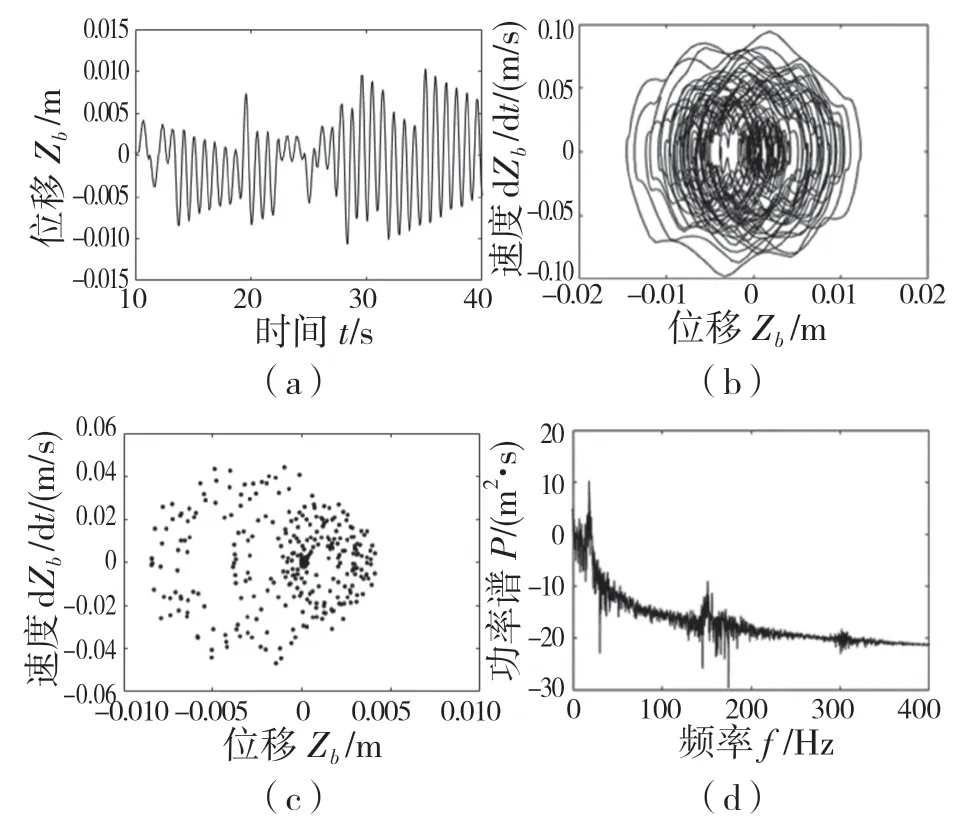
图5 f=14 Hz 时系统各参数曲线和图谱Fig.5 System parameter curve and graph (f=14 Hz)
(4)第4 组(f=17 Hz)
由图6 所示,时间历程图稳定,相轨迹出现上下不同圆环,庞加莱(Poincaré)截面近似形成封闭的圆环,功率谱开始出现不连续趋势。由混沌识别方法可知,该七自由度车辆系统由混沌运动向周期运动状态过渡。
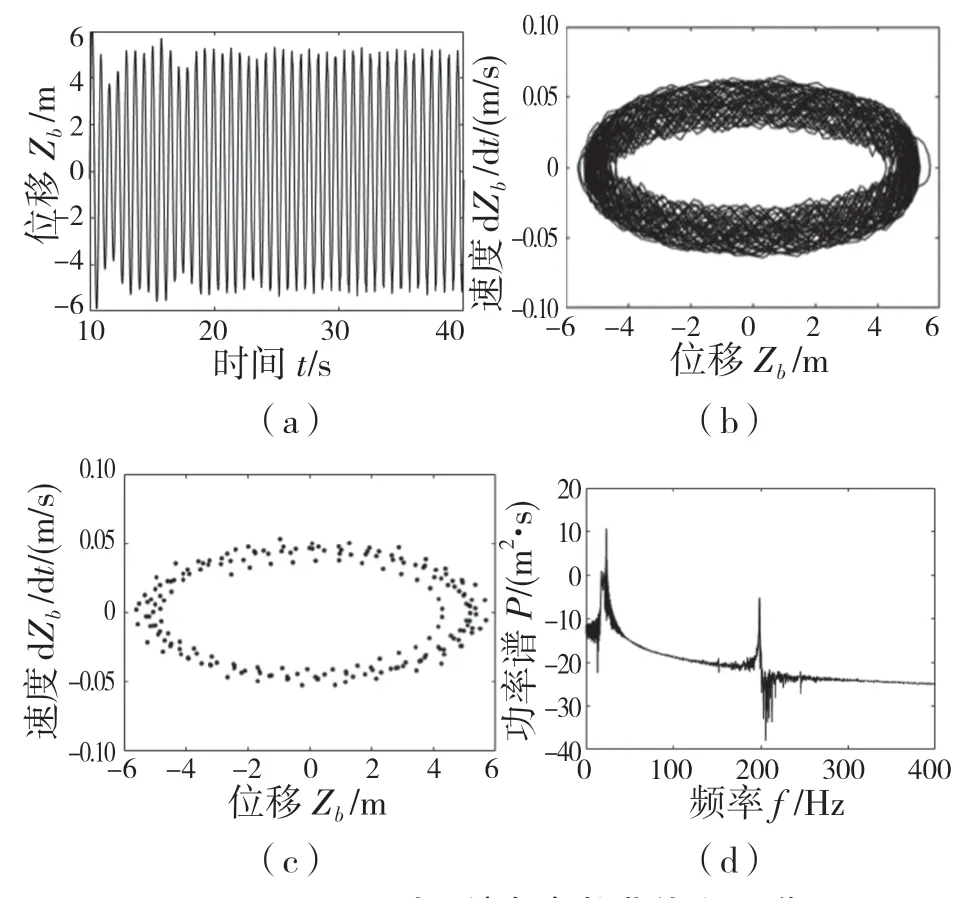
图6 f=17 Hz 时系统各参数曲线和图谱Fig.6 System parameter curve and graph (f=17 Hz)
3 结语
本文采用数值分析法,对整车七自由度仿真模型在正弦路面激励下进行混沌特性研究分析。通过分岔图、相轨迹、庞加莱(Poincaré)截面、功率谱及计算最大Lyapunov 指数,判断非线性悬架系统是否能够进入混沌状态,大致确定了悬架系统进入混沌状态的临界条件,并发现系统运动状态随着非线性因素改变,会发生运动状态的变迁。考虑到车辆系统运动状态的复杂性,且在特定情况下极可能从周期运动演变为混沌运动,本研究可为悬架系统的设计和改进提供理论参考。
