基于Budyko假设的汾河上游水源区径流衰减归因分析

蔺彬彬，张亚琼，郭维维

（1.太原理工大学水利科学与工程学院，太原030000；2.山西漳河水务有限公司，太原030000）

气候变化和人类活动的双重影响是导致径流规律发生变化的两大主要因素，气候变化尤其是降雨导致径流在时间和数量上都发生了变异，破坏了径流序列的一致性；人类活动通过改变下垫面条件，使流域产汇流过程发生变化［1］。全球平均气温在20世纪约升高了0.6 ℃，IPCC的研究表明全球气温在21世纪末可能增高1.1～6.4 ℃。在1957-2003年期间山西省降水量总体呈减少趋势，减少速率为-17.3 mm/（10 a），显著高于全国水平；气温总体呈上升趋势，增长率为0.15 ℃/（10 a）［2］。汾河是山西的母亲河，黄河的第二大支流，进入20世纪80年代，随着气候变化及经济社会的不断发展，汾河入黄径流量衰减明显［3］，天然径流量的减少，严重影响了流域内经济社会的发展，加剧了流域内生态环境的恶化。汾河上游作为汾河的重要水源区，也是山西省会太原市重要的地表水水源地，同时也处在岩溶地下水水源涵养区和保护区［4］，近几十年来汾河上游流域径流衰减明显，针对这一事实进行定量分析，对深入理解汾河流域水文演变规律，对未来气候变化和人类活动加剧背景下水资源适应性管理都具有重要的意义。

针对流域径流变化的原因，不同学者采用不同的方法进行了分析。例如，刘昌明等［5］应用SWAT 分布式水文模型研究了气候变化对黄河河源区径流及蒸散发的影响；马欢等［6］基于GBHM 模型分析了气候变化和人类活动对密云水库入库径流量急剧减少的贡献率；张树磊等［7］应用Budyko 假设水热平衡理论对1960-2010年期间我国主要河流上游山区小流域的径流衰减进行了定量归因分析，研究发现降雨量的减少和人类活动引起的下垫面的变化是径流减少的主要原因；张连鹏等［8］以渭河的北洛河流域为研究对象，应用Budyko 假设和TOPMODEL 水文模拟方法定量分析径流衰减的原因，并两种方法进行了对比，发现分析的结果具有较好的一致性。

总的来看，目前针对径流衰减归因分析的方法主要有两种：一是基于水文模拟法，二是基于Budyko假设的弹性系数法。而基于水热平衡理论的Budyko假设方法，由于其方法简单且输入的参数少，在定量解析径流衰减原因方面已得到了广泛的应用。在流域尺度下，实际蒸散发除受能量供给条件和水分供应条件的影响外，植被、土地利用等下垫面条件也是影响蒸散发变化的重要因素［9］。因此，涉及流域下垫面条件的Budyko 修正模型逐渐发展起来，实现了Budyko 假设的参数化。2006年，杨大文教授［10，11］在已有的蒸散发互补理论研究的基础上，基于Budyko 假设提出了流域水热耦合平衡方程，即Choudhury-Yang公式。该公式引入了反映流域下垫面特征的参数n，且表达式相对简单，已得到广泛的应用。本文将该公式应用于汾河流域上游水源区，来定量解析汾河上游水源区径流衰减的原因，为山西省正大力开展的汾河流域清水复流及水源区保护工程提供技术支撑。

1 研究区及数据说明

以汾河上游汾河水库水文站控制流域为研究区，地理位置如图1，控制流域面积5 268 km2，属亚热带大陆性季风气候，为半干旱、半湿润型气候过渡区，四季分明，春季多风干燥，夏季多雨炎热，秋季少晴早凉，冬季少雪寒冷。雨热同期，光热资源较为丰富，有利于农业发展。多年平均温度7.19 ℃，多年平均降水量465 mm，降水年际变化较大，无霜期大于130 d。

采用汾河水库水文站1961-2016年期间的径流数据；流域内29 个雨量站的雨量数据；流域内3 个气象站及周边8 个气站的数据，包括降雨、气温、日照时长、风速和相对湿度等。根据联合国粮农组织推荐的Penman-Monteith 公式来，利用11 个气象站点的气象数据，计算气象站点的潜在蒸散发量，利用反距离加权法（IDW）插值生成网格数据求平均，得到流域平均潜在蒸散发量。基于29个雨量站的雨量数据，利用泰森多边形来计算流域的面雨量。

2 研究方法

2.1 趋势性和变异性的检测方法

Mann-Kendall 趋势检验法是世界气象组织（WMO）推荐并已广泛应用的一种非参数统计检测方法，非参数不要求样本遵循一定的分布，也不受少数异常值的干扰，且计算简便，常被用来检测水文气象长时间序列参数的显著性趋势，因此选取此方法来判定径流、降雨、潜在蒸散发的变化趋势及径流变化的突变点。由MK 检验法得到统计值Z，当Z＞0 时，说明参数系列呈增加趋势；当Z＜0时，说明参数系列呈减少趋势。

2.2 Budyko假设及Choudhury-Yang公式

前苏联著名气候学家Budyko通过研究发现，陆面长期实际蒸散量是由陆面的水分条件和能量条件之间的平衡决定的［10］，并认为可用潜在蒸散发量（PET，简称E0）表征流域水循环的能量条件，降水量P表征流域水循环的水分条件。基于此Budyko提出了陆面实际蒸散量的两个边界条件，一个是像沙漠地区的极端干旱情况（E0/P→∞），所有的大气降水都被用于蒸散发（E/P→1）；另一个是在极端湿润情况下（E0/P→0），水分供给充分所有可用于蒸散的能量都被用于蒸散发，全部转化为潜热（E/E0→1）。

在假定边界条件的基础上，Budyko 提出了满足上述边界条件的水热耦合平衡方程的一般形式：

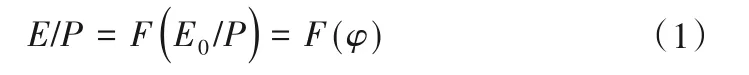
式中：E、P分别为流域多年平均的年实际蒸散发量和降雨量；φ为干旱指数（φ=E0/P），是气候带和植被带划分的基础；E0为流域多年平均的年潜在蒸散发量。

理论上，Budyko 框架的水量-能量耦合平衡方程具有普适性，这点得到很多研究的证实，然而仍有很多流域的观测资料与Budyko 理论曲线存在一定偏差。因此，很多研究者对Budyko 理论曲线模型不断发展与丰富，提出了不同的估算公式，但大多数公式是基于特定流域推算出来的，具有一定的局限性，至今尚未获得全球普适的估算方法。对此杨大文等［11］引进了一个参数n来调整因下垫面差异引起的偏差，经过推导得到新的公式：

式中：n为下垫面特征参数，表征了流域植被、土地利用、地形地貌的情况，并认为P，E0，n是相互独立的变量。

2.3 径流弹性系数

在一个闭合流域，流域的水量平衡可用下式来表示：

式中：P为流域多年平均降雨量；R为流域多年平均河川径流量；E为流域多年平均实际蒸散发量；ΔS为时段内流域蓄水量的变化，对于长历时ΔS可以忽略不计，近似为0。

结合式（1）～（3），流域长历时年均径流量可由下式来计算：

年径流量R的变化可以表示为如下全微分形式：

Schaake［12］将径流的降雨弹性系数（εP）、径流的潜在蒸散发弹性系数（εE0）、径流的下垫面弹性系数（εn）；分别定义为εP=

将式（5）除以多年平均径流深R，可以得到：

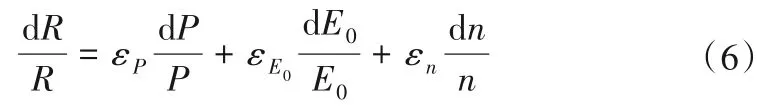
利用式（4）分别对参数P、E0、n求偏导，求得弹性系数εP，εE0，εn表达式如下：

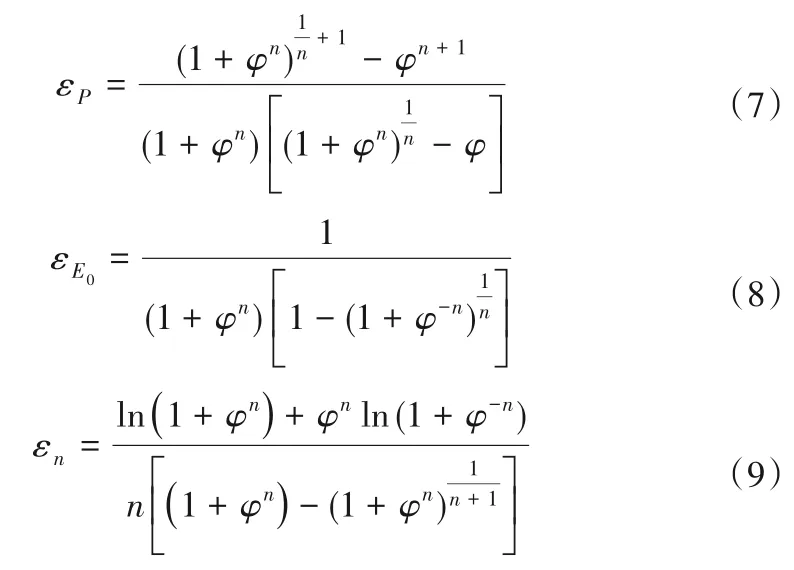
这3个弹性系数反映了流域多年平均的水文气候和下垫面特征，如果设定εP，εE0，εn的值分别为a，b，c，那么εP表示：如果P增加1%，将驱动径流量R增加a%（或减少b%）；εE0表示：如果E0增加1%，将驱动径流量R减少b%；εn表示：如果n增加1%，将驱动径流量R减少c%。

2.4 径流变化归因分析

在人类活动和气候变化的影响下，径流总的变化可以表示为：

式中：ΔRtot为径流总的变化量；为基准期多年平均径流量；为变化期多年平均径流量。

总的径流变化量可以表示为：

根据弹性系数εP，εE0，εn，可分别按下式求得ΔRP，ΔRE0，ΔRn。

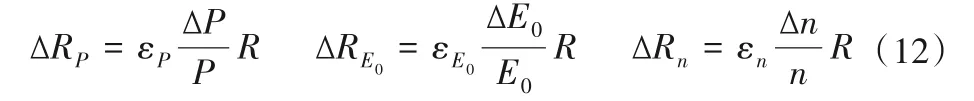
式中：ΔP，ΔE0，Δn分别表示流域基准期和变化期年均降雨量、年均潜在蒸发量、下垫面参数的变化量；nbas和nvar分别代表基准期和变化期下垫面参数，可由式（2）反推得到。

3 结 果

3.1 径流、降雨及潜在蒸散发趋势分析

对1961-2016年汾河水库站56年的年径流系列进行统计分析，通过趋势线及5年滑动平均分析（图2），通过M-K 检验方法，计算年径流系列的MK 统计值为-3.79，都说明年径流呈显著下降趋势，且通过了0.05显著性水平检测，年径流深以8 mm/（10 a）的速率在递减。通过M-K 突变分析（图3）发现1961-2016年期间汾河水库站的年径流量在1980年发生了突变，因此将1980年设置为突变点。据此，在进行径流衰减归因分析时，将1961-1980年划分为基准期，将1981-2016年划分为变化期，基准期和变化期年径流深的平均值分别为77.8 mm 和50.2 mm，径流深衰减了27.6 mm，将近35.5%。

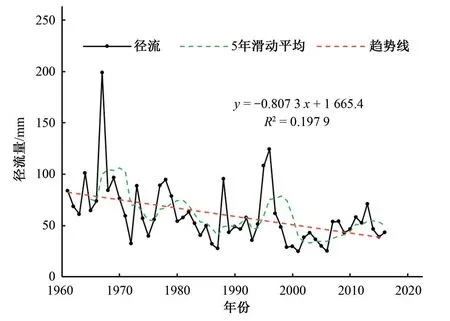
图2 汾河水库站年径流趋势分析Fig.2 Long-term trend of annual-runoff at Fenhe reservoir station

图3 汾河水库站年径流M-K突变分析Fig.3 M-K mutation analysis of annual-runoff at Fenhe reservoir station

研究区年降雨量MK 统计值为-0.163，说明年降雨量呈现不显著的下降趋势，长系列趋势分析见图4。研究区年潜在蒸散发量MK 统计值为1.97，说明年潜在蒸散量呈增加的趋势，长系列趋势分析见图5。基准期和变化期研究区年均径流深、年均降雨量、年均潜在蒸散发量的统计见表1。

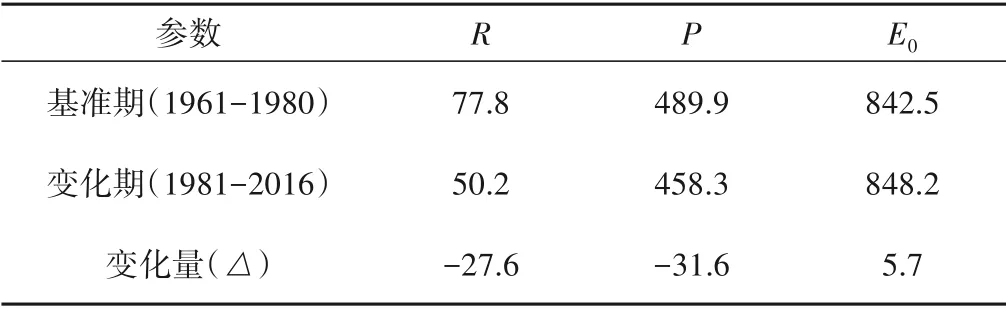
表1 基准期和变化期的参数统计表 mmTab.1 The value of R，P，E0 and n in base-period and change-period

图4 研究区年降雨量趋势分析Fig.4 Long-term trend of precipitation

图5 研究区年潜在蒸发量趋势分析Fig.5 Long-term trend of potential evapotranspiration

3.2 径流弹性系数计算

根据研究区1961-2016年的年降雨量、潜在蒸散发、径流深，推求长系列年均值，计算干旱指数，根据公式（4）求解研究区下垫面参数n，根据公式（7）～（9）分别求得径流的3 个弹性系数，计算结果见表2，说明当流域年降雨量增加（减少）1%时，将导致径流量增加（减少）2.64%；年潜在蒸散发量增加（减少）1%时，将导致径流量减少（增加）1.64%；下垫面参数n增加（减少）1%时，径流流量减少（增加）1.89%。

表2 研究区特征及径流弹性系数Tab.2 The characteristic and runoff elasticity coefficient of research area

3.3 径流变化归因分析

在1961-2016年期间，径流发生突变的1980年前后，基准期和变化期径流深（R）、降雨（P）、潜在蒸散发（E0）及下垫面参数（n）的统计值见表3。变化期和基准期的下垫面参数n，分别根据公式（4）求解得到。基于研究区基准期和变化期年均降雨、年均潜在蒸散发及下垫面弹性系数的值，利用求得的弹性系数，根据公式（14）分别计算由于三者驱动引起的径流变化量，并分别计算贡献率。从表3可以看出汾河水库站控制流域，变化期相对于基准期多年平均降雨量减少了31.6 mm，驱动径流量减少了10.6 mm，贡献率为39.7%；潜在蒸散量增加了5.7 mm，驱动径流量减少了0.7 mm，贡献率为2.5%；两者之和就是气候变化对径流衰减的贡献率为42.2%。而人类活动引起的下垫面改变，导致变化期下垫面特征参数n增加了0.269，驱动径流量减少了15.4 mm，对径流衰减的贡献率为57.8%。由此可说明，1961-2016年汾河流域上游水源区径流衰减的主要原因是人类活动引起的下垫面变化，其次是降雨的减少。

表3 径流变化归因分析 mmTab.3 Attribution analysis of runoff attenuation

变化期与基准期相比下垫面参数n增加了0.269，说明在人类活动的影响下汾河上游下垫面情况发生了较大的变化。从20世纪80年代，在政府主导下的汾河上游进行了大规模的水土保持措施，主要包括大规模的植树造林及退耕还林还草，建设淤地坝，修建基本农田。邸富宏［13］基于MODIS数据对汾河上游植被动态进行了监测，研究发现2000-2010年来，汾河上游区域NDVI最大值呈上升趋势，NDVI随年份的增长率为7.8%/（10 a），植被覆盖明显改善；党晋华等［14］对汾河上游区域土地类型变化进行了分析，发现2000-2013年森林为最活跃的土地利用类型，湿地和森林在空间上呈现扩张的发展趋势。植被覆盖的增加在改善区域生态环境、水源涵养及治理水土流失方面具有重要的意义，但由于流域实际蒸散发的增加，导致产流量的减少。另外汾河上游部分区域地处山西六大煤田之一的宁武煤田，当地的煤矿开采，形成大面积的采空区，导致地表变形、塌陷，地层中的裂隙增多增大，地表形成大量的裂缝，降雨入渗量增大产流系数减少。

4 结 论

汾河上游作为汾河流域重要的水源区，1961-2016年期间年径流量呈现显著的下降趋势，变化期相比基准期减少了35.5%，应用基于Budyko假设的水热耦合平衡理论，对径流衰减的原因进行了解析。研究发现，汾河上游由于人类活动引起的土地利用、植被覆盖、地形等下垫面特征参数的改变是导致上游径流衰减的主要原因，相应的贡献率接近60%，其次是降雨减少导致的。汾河上游大规模开展的水土保持措施及长期的煤矿开采，导致下垫面条件发生了较大的变化，从而增加了流域的实际蒸散发，导致降雨入渗量增多。研究表明制定科学合理水土保持措施，低影响的煤炭开采方式及采空区的修复治理，对现在山西省正在大力开展的汾河流域水生态修复及清水复流工程具有重要的意义。