基于ESMD的西江流域降水时空变化特征分析

李继清，陈思雨

（华北电力大学水利与水电工程学院，北京102206）

0 引 言

气候与人类社会生活密切相关，随着全球变暖问题日益严重［1］，进一步加剧了降水这一气候基本因子的时空分布差异，进而对水资源、生态环境系统以及人类的生产生活产生影响。西江流域拥有丰富的水资源，降水是其径流的补给来源，决定径流分布情况。研究西江流域降水中长期的时空变化特性，能够掌握该流域水文资源的周期、趋势和突变规律，为该地区的水资源利用和管理提供科学依据。

气候由多个时空尺度构成了多层次结构，是一个具有非平稳性的非线性复杂系统。气候变化特性研究领域已有较为系统的分析方法，所采用的数学分析方法也在逐步改进和完善。早期研究中多采用累积距平、等值线等方法［2-5］，后期逐渐引入数学分析法，国内外在研究各地区降水变化时广泛采用Mann-Kendall 检验法［6，7］，并结合小波分析等多种方法进行对比［8-12］。此外，有序聚类、全球气候模型等方法也可应用于气候分析［13-17］。但传统方法受其理论基础限制，在实际应用中存在一定的局限性，极点对称模态分解（Extreme-point Symmetric Mode Decomposition，ESMD）法作为近年来发展起来的局部自适应时间序列分析技术［18］，善于从非平稳、非线性的观测序列中寻找变化趋势并对其做出异常诊断。王金良和李宗军［19］以及房贤水［20］分别从ESMD 方法统计特征、工作原理等方面对其优势进行了论证。近年来，该方法也逐渐应用到气候变化的实例研究［21-23］，进一步验证了其优势和可靠性。本文采用ESMD 法，对西江流域的降水观测资料进行周期、突变及趋势分析，并与线性趋势分析、Mann-Kendall 检验法和小波分析法的分析结果进行对比验证，进而详细分析西江流域的降水时空变化特征，为流域水资源的开发利用提供决策依据。

1 研究方法

极点对称模态分解法（ESMD）能够通过模态分解和时-频分析，全面分析时间序列的周期、突变和趋势特征，在水文时间序列分析领域具有较好的优势。分别利用线性趋势分析法判别数据序列的整体线性变化趋势，Mann-Kendall 检验法判别数据数列的变化趋势和突变时间点，小波分析法提取数据序列的周期特征，与ESMD方法的计算结果进行对比分析。

1.1 极点对称模态分解法（ESMD）

极点对称模态分解（ESMD）方法在希尔伯特-黄变换法之上发展而来，在保留了经验模态分解法优点的同时也解决了其中存在的“模态混叠问题”，该方法在气候分析中的优势为：擅长寻找变化趋势，能够分离出数据序列的年际变化趋势和整体趋势；擅长异常诊断，能够观察数据序列各模态中的异常时频段；擅长时-频分析，采用直接插值法能够更为直观地分析各时间尺度上的频率变化［24］。

第一部分模态分解具体计算步骤如下：

（1）找出序列X的全部极值点，包括极大值点和极小值点，并将它们依次记作Ei（i=1，2，3，…，n）；

（2）用线段连接所有相邻的极点并将线段中点依次记为Fi（1≤i≤n-1）；并通过一定方式补充左、右两端边界中点F0和Fn；

（3）利用所获取的n+1 个中点构建p条内插曲线L1，…，Lp（p≥1），并计算其均值曲线L*；

（4）对X-L*序列重复上述步骤，直到|L*|≤ε 或者筛选次数达到预设的最大值K，得到第一个经验模M1；

（5）对剩余序列X-M1重复上述4 个步骤，直到剩余序列R只剩余一定数量的极点，便可分别得到经验模M2，M3，…；

（6）让最大筛选次数K在整数区间［Kmin，Kmax］内变化并重复上述几个步骤。计算方差比率，并画出随K的变化图，找出方差比率最小值对应的最大筛选次数K0，此时分解得到的趋势余项R为数据的最佳拟合曲线。以K0作为限制条件再次重复上述步骤，得到最佳分解结果。最终利用ESMD 方法将序列X分解为一系列经验模态和一个趋势余项。

第二部分时-频分析认为应当尊重离散数据的离散性特征，提出了针对数据的“直接插值法”，不但可以直观地体现各模态的振幅与频率的时变性，还可明确地获知总能量变化。直接插值法基本思路如下：

（1）寻找极值点，计算两个相邻极大值点和相邻极小值点之间的时间差；

（2）将这些时间段视为局部周期赋给其中点，画出时间-周期对应点图；

（3）将这些局部周期值取倒数得到局部频率，再做3次样条插值得到光滑的时间-频率变化曲线［25］。

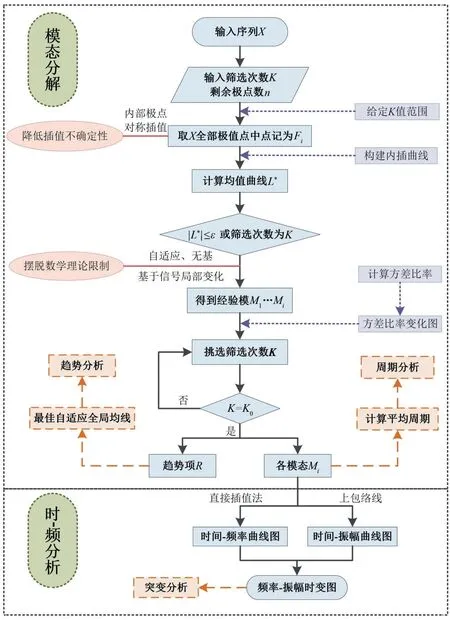
图1 ESMD方法流程图Fig.1 The step of ESMD

1.2 对比验证方法

1.2.1 线性趋势法

线性趋势法能够对数据序列的线性变化趋势进行分析。用yi表示样本量为n的气候变量，ti为对应时刻，建立一元线性回归方程：

式中：a为回归常数；b为回归系数即气候变量的倾向趋势［26］。

1.2.2 Mann-Kendall检验法

Mann-Kendall 检验法是一种非参数统计检验方法，广泛应用于水文序列的趋势、突变特征分析。利用M-K 统计值Z进行趋势统计的显著性检验，先假设该序列无趋势，通过两尾检验，在给定显著性水平下，查得临界值Z1-α/2，当|Z|＜Z1-α/2时，接受原假设；若|Z|＞Z1-α/2，则拒绝原假设。进行突变分析需要计算M-K统计值UFk和UBk：

通过分析UFk和UBk交点位置即可明确突变发生时间［27］。

1.2.3 小波分析法

小波分析的基本思想是用一簇小波函数系来表示或逼近某一信号或函数。在小波变换系数Wf（c，d）中，将小波变换系数的平方值在d域上积分可得到小波方差：

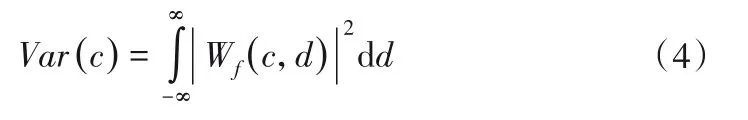
式中：c为伸缩尺度；d为平移参数。

小波方差随尺度c的变化过程为小波方差图，能够反应信号波动的能量随尺度c的分布，进而获得数据序列的周期变化规律［28］。

2 研究结果与分析

采用ESMD 法对于西江流域的降水资料进行模态分解和时-频分析，结合线性趋势分析、Mann-Kendall 检验法和小波分析法，对各降水系列的周期、突变和趋势特征进行分析讨论。

2.1 研究区概况及数据资料

西江是珠江流域的主干河流，发源于云南省，流经地区地势西北高东南低，全长共2 075 km，主要河流由南盘江、红水河等河段组成。西江流域属于亚热带气候区，春夏季降雨充沛，秋冬较为干旱，水资源量变化主要受到降水季节分配的影响，径流年内分配极不均匀，汛期径流量比例占年径流量的80%以上。降水量由东到西呈现递减趋势［29］。

分析数据来自于西江流域1954-2008年51 个气象站的日降水资料，空间分布如图2，基本能够均匀覆盖西江整个流域。对日降水资料进行整理计算，得到西江流域年降水、年降水极大值、年降水极小值、汛期降水和非汛期降水数据系列。其中年降水极值为全年日降水极大或极小值。根据地理情况将西江流域划分为500 m 以上的上游高原区以及500 m 以下的中下游平原盆地区。平原区年降水Cv值为0.121，高原区年降水Cv值为0.089，图3为两地区年降水量对比。高原区年降水量约为1 100 mm，平原区年降水量约为1 500 mm，两地区降水趋势基本相同。

图2 西江流域气象站分布图Fig.2 Distribution of meteorological stations in the Xijiang River Basin

图3 西江流域平原区和高原区年降水概况图Fig.3 Annual precipitation in the plain and plateau of the Xijiang River Basin

2.2 周期性

ESMD 法具有自适应性和基于信号的局部变化特性，能够更好地提取非平稳、非线性序列的变化规律。通过ESMD 法对西江流域各降水序列进行模态分解，可得到3～5 个模态分量以及一个趋势项余量R，玉溪和连县年降水分解结果图4，各模态分量能够反应原数据序列中固有的振荡特征，即对应为降水序列的周期规律。表1为各降水序列的周期结果。西江流域各站之间各降水序列的固定周期成分均出现接近或相同的情况，具有统一的空间周期特征。

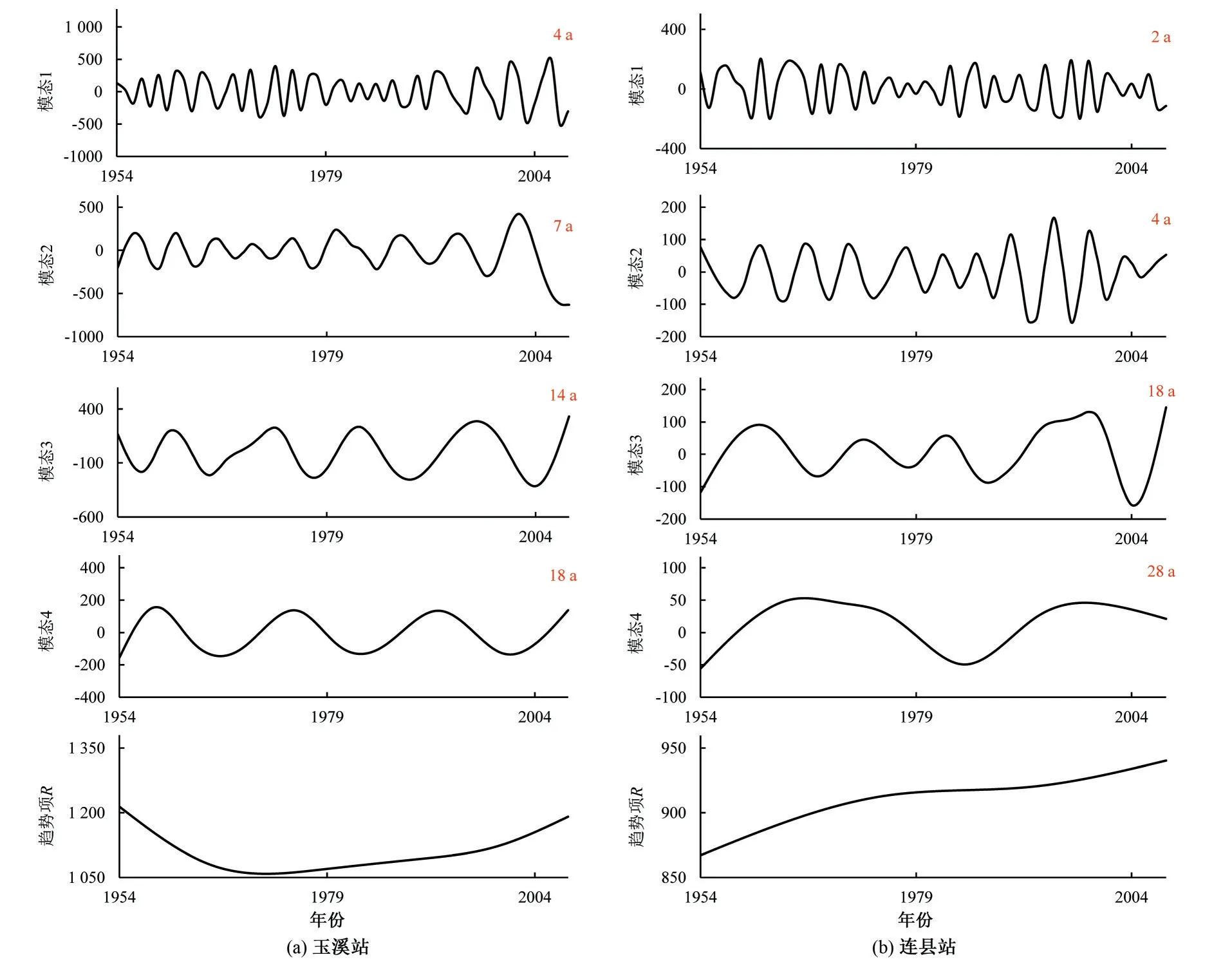
图4 年降水模态分解图Fig.4 Exploded modal decomposition maps of annual precipitation

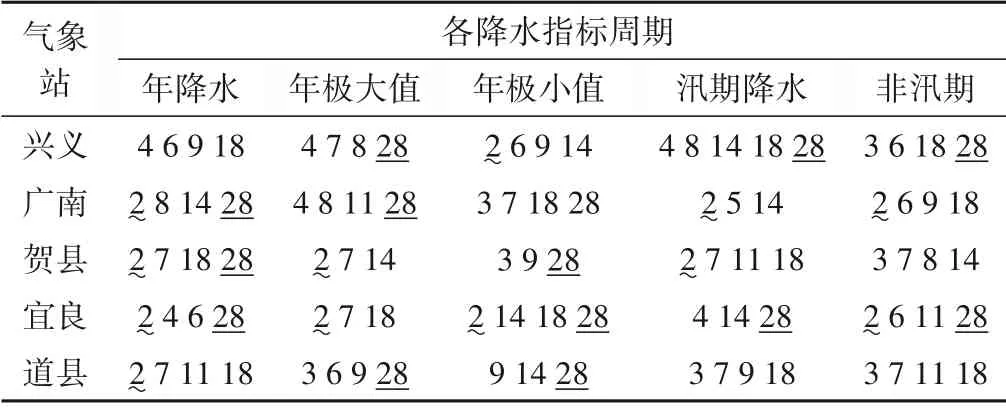
表1 西江流域内各站各降水指标周期统计表 aTab.1 Periodic statistics of precipitation indicators at stations in the Xijiang River Basin

对西江流域各站各降水指标周期成分出现次数进行统计整理，结果如图5。其中橙色代表年降水，紫色代表年降水极大值，绿色代表年降水极小值，黄色代表汛期，蓝色代表非汛期。年降水18 a 的周期规律在站中出现频率最高，其次为28 a 的周期特征。年极大值和年极小值的周期规律出现频次最高的均为28 a，其次为2 a、14 a 等。汛期降水以存在3 a 和28 a 的周期特征最为普遍。非汛期降水序列中84%的气象站存在2 a 的周期变化特征，其次是28 a 和18 a。各降水指标之间的周期特征具有较高一致性，主要存在2、14、18和28 a的周期变化规律。

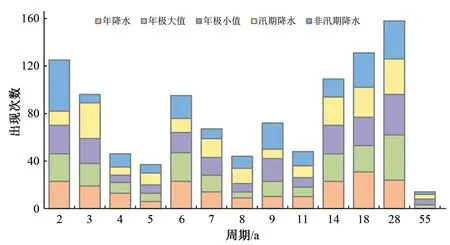
图5 各降水指标周期成分出现次数统计图Fig.5 Statistics of the number of occurrences of the periodic components of various precipitation index

采用小波分析法与ESMD 方法周期分析结果进行对比，表2为贵阳、罗甸、通道和威宁年降水的周期对比结果。两方法下存在部分一致或相近的周期结果，周期越短结果一致性越好，周期越长越容易出现差异。究其原因，小波分析是以傅里叶变换为理论依据，在小波基选取等方面存在一定局限性，限制了该方法的实际运用效果。而ESMD方法具有较强的灵活性和自适应性，可通过数据自身特点进行分解，探索事物的内在规律。

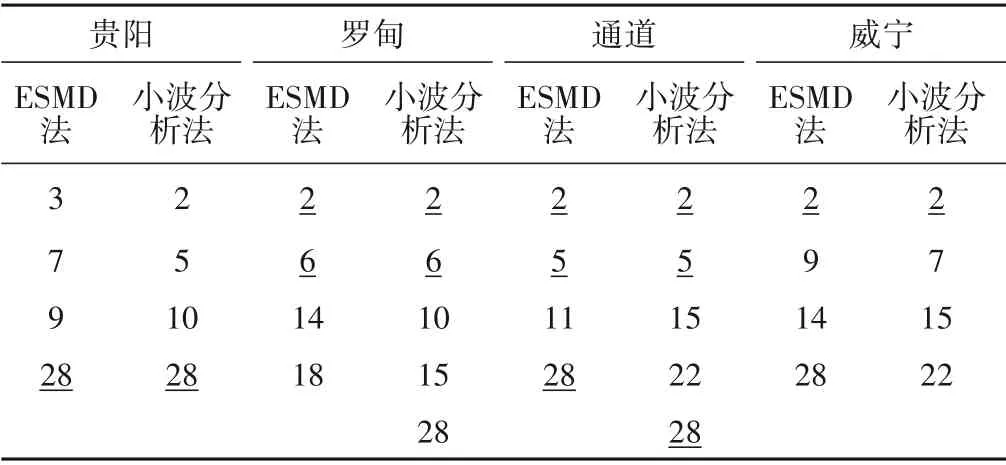
表2 ESMD法和小波分析法下年降水周期对比结果表 aTab.2 Comparison of sudden changes in precipitation in the next year by ESMD method and wavelet analysis

2.3 突变性

根据ESMD 法得到的数据序列模态分量，采用直接插值法得到其对应的频率-振幅时变图，如图6为玉溪和连县站年降水时-频分析结果图，其中F代表频率，A代表振幅，根据两者对应关系，可知图像在出现低频、大幅度振荡和高频、小幅度振荡时均代表数据序列发生了降水突变。对比图中F和A的变化情况，可知玉溪年降水在1983年和1993年发生，连县年降水在1971年发生突变。

图6 年降水频率-振幅时变图Fig.6 Frequency-amplitude time-varying data of annual precipitation

通过观察频率-振幅时变图得到各降水序列突变年份，结果整理统计如表3。空间上，各降水指标在站间的突变结果均不完全一致，在相邻站间突变结果一致性稍高，图7梧州、广宁、高要3 个相邻气象站的年降水均在观测期内发生三次突变现象，且突变时间较为接近。但降水突变在西江流域整体空间范围内未显示出明显的空间分布规律和特征。

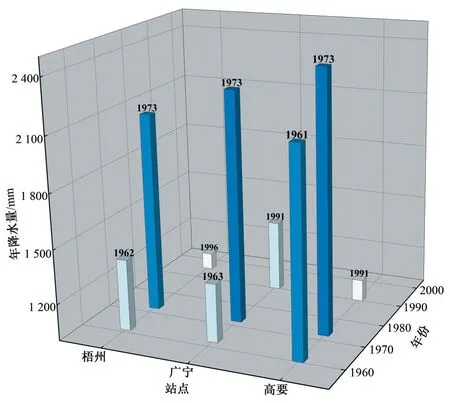
图7 梧州、广宁和高要站的年降水突变结果图Fig.7 Abrupt changes in annual precipitation at Wuzhou，Guangning and Gaoyao stations

表3 西江流域内各站各降水指标突变年份统计表Tab.3 Statistics of abrupt change of precipitation index of each station in Xijiang River Basin

通过整理各降水指标的突变时间点分布年代，分析突变的时间分布特征，结果如图8。各降水指标在各年代内均有突变现象发生，其中年降水和汛期降水的突变结果相似，均在20世纪60年代出现突变现象最为频繁，其次为90年代；非汛期降水在80年代出现突变现象的次数最多，60年代的突变次数与汛期降水持平。年极大值的突变现象频发于60年代和90年代，年极小值则在80年代出现突变情况最多。各降水指标突变现象多集中在60年代、80年代和90年代，在50年代和00年代较少发生突变。

图8 各降水指标突变时间出现年代统计图Fig.8 The chronological statistics of the abrupt time of each precipitation index

将ESMD 法与Mann-Kendall 检验法结果进行对比分析，图9为玉溪和连县的年降水M-K 结果图，其中玉溪在1956年、1977年、1993年、2001年和2008年发生降水突变，连县站的突变年份为1960年、1963年、1970年和1986年。

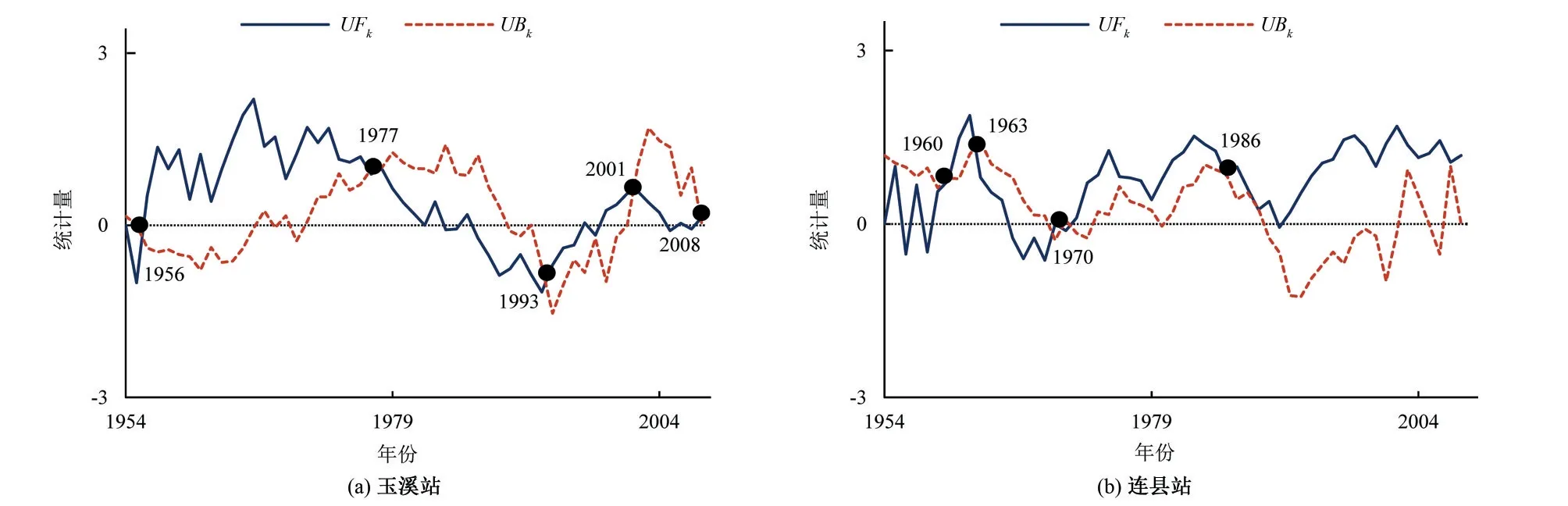
图9 年降水M-K图Fig.9 Results of annual precipitation based on M-K method

表4为蒙自、独山、钦州和百色站年降水M-K法和ESMD法的突变结果对比。虽然两方法算得突变结果不完全一致，但均存在相近或相同的突变结果，可知ESMD 方法进行西江流域各降水序列突变分析具有一定的可靠性。两方法相比，M-K 法仅能对数据序列中的突变点进行判别，而ESMD 方法能够在通过各模态频率与振幅的对应关系判断数据序列突变点的同时了解其局部变化情况，具有明显优势。

表4 ESMD法和Mann-Kendall检验法下部分站年降水突变年份对比结果表Tab.4 Results of abrupt change in precipitation of some stations under the ESMD method and the M-K test

2.4 趋势性

线性趋势分析能够判别西江流域各降水指标的多年线性变化特征，统计结果如表5。年降水、年极大值和汛期降水线性趋势分布情况相似，正、负增长站数基本持平，3 个指标的正增长率最大均为防城站，负增长率最大均为南宁站，其中年极大值的线性变化速率略小，多不超过1 mm/a，年降水和汛期降水线性变化速率多不超过4 mm/a。年极小值和非汛期降水的线性趋势多为正增长，但线性变化趋势均不显著，年极小值正增长率最大为连县站，负增长率最大为融安站，非汛期降水的正增长率最大为靖西站，负增长率最大为高要站。

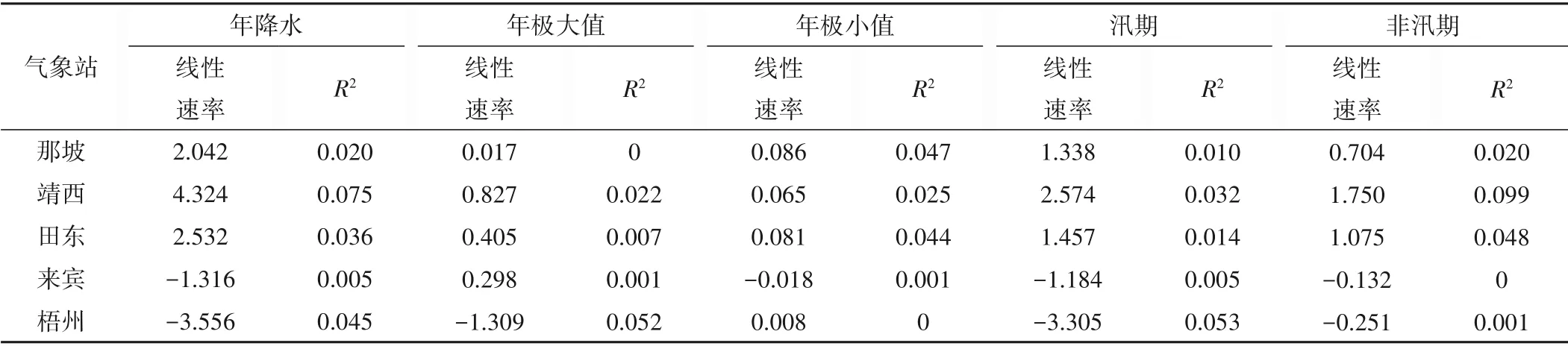
表5 西江流域各站各降水指标线性变化速率结果表Tab.5 Results of the linear change rate of precipitation indexes at various stations in the Xijiang River Basin

ESMD 方法模态分解得到的趋势项R可描述降水序列的具体变化过程，进而分析西江流域各降水指标趋势特征。图10为年降水指标的变化趋势类型，主要变化趋势为上升-下降-上升型和先降后升型，多分布于中下游地区，除此以外上游高原区域存在少量的先升后降型和下降-上升-下降型。年极大值指标的变化趋势以上升-下降-上升、先升后降以及先降后升型为主，其中前两种变化类型均多分布于流域中下游，此外上游地区还存在少量持续上升和下降-上升-下降的变化特征。年极小值指标中，持续上升型、先降后升型、先升后降型等多种变化类型数量较为均匀，在流域内交错分布。汛期降水与年降水分布情况相似，出现了少量站点呈现持续下降的变化特征。非汛期降水指标中近半数站呈现先升后降的变化特点，多分布于流域中下游。由此可见，西江流域中下游地区各降水指标变化趋势类型较为统一，而位于流域西部的上游地区由于山区地形因素影响，各降水指标的趋势变化存在较大差异。

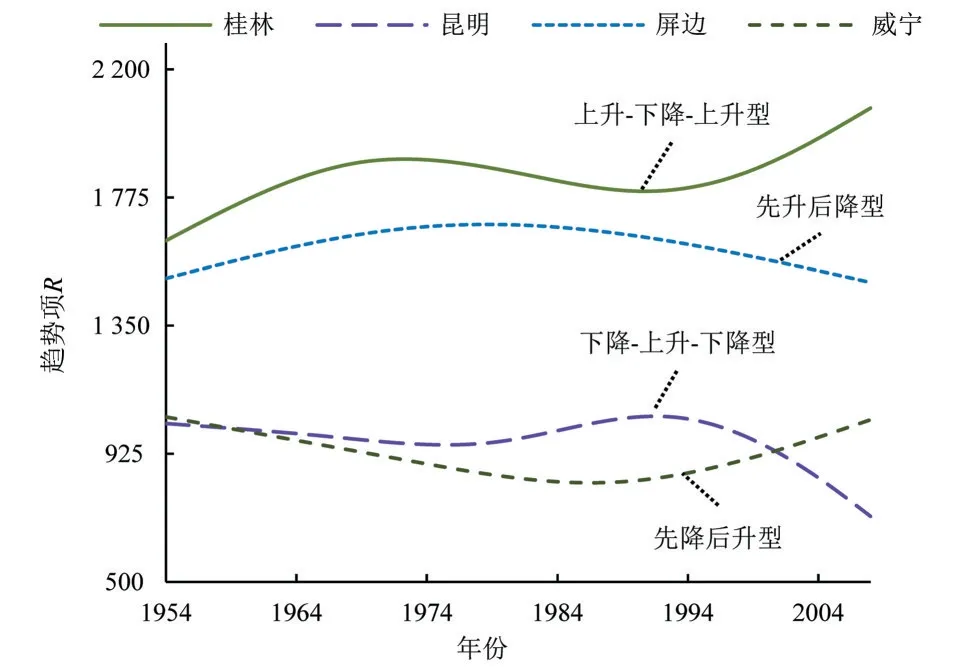
图10 ESMD方法下年降水的各类变化趋势图Fig.10 Various trends of annual precipitation based on the ESMD method

采用M-K 趋势检验法对ESMD 法的趋势结果进行对比分析，M-K 趋势检验法给定显著水平α=0.05，临界值为±1.96，两方法计算得到的桂平站年降水趋势结果对比如图11。在M-K法分析中，桂平站年降水前期呈现较为平稳的小幅波动，在90年代后呈现增长趋势，整体降水序列M-K 统计值Z为1.19，表现为不显著上升趋势，与ESMD 法的趋势结果具有较高的一致性，证明采用ESMD方法分析数据序列的趋势性具有可靠性。

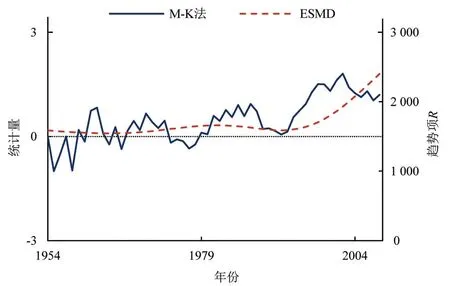
图11 桂平站年降水ESMD法与M-K法趋势结果对比图Fig.11 Comparison of trend results of ESMD and M-K methods of annual precipitation at Guiping station

3 结 论

气候变化与水文资源有着密切关联，通过研究降水变化特性能为流域水资源管理提供有效手段。在气候分析领域，ESMD 方法的优势在于能够更为全面有效地识别数据序列的趋势、周期和突变特征。采用ESMD 方法结合小波分析等对比方法分析西江流域的各降水指标变化特征，得到如下结论：①西江流域各站的降水指标周期特征具有统一性，主要存在2、14、18、28 a等周期规律；②每个站的各降水序列均存在1～5个突变点不等，各降水指标突变多集中在20世纪60年代、80年代和90年代；③年降水、年极大值和汛期降水的正、负增长线性趋势站数量基本持平，年极小值和非汛期降水的线性趋势多呈现出上升现象；④年降水和非汛期降水在中下游区域的ESMD 法趋势变化具有较高的一致性，其余各降水指标的变化趋势多呈现散乱分布。

在全球变暖环境下，西江流域降水指标年内、年际周期变化规律相近，年极小值及非汛期降水量统一呈现微弱增长趋势，中下游地区降水指标趋势特征相对一致，降水偏多和偏少时期交替出现，但由于地理位置等因素影响，各站点仍存在其独有的突变和趋势特征，需进一步探寻各水文要素的变化特性及各要素之间的相关联系和影响机制。