HOUGH变换检测线段IP设计

2021-07-02吴相涛桑红石

通信电源技术 2021年5期

吴相涛，桑红石,3

（1.华中科技大学人工智能与自动化学院，湖北武汉 430074；2.多谱信息处理技术国防科技重点实验室，湖北武汉 430074；3.图像信息处理与智能控制重点实验室，湖北武汉 430074）

0 引言

线段识别和定位在图像处理领域如机场跑道和桥梁检测识别等有着重要应用，这些处理任务往往有图像信息大、实时性要求高且资源消耗大等特点，纯软件的处理方式难以满足系统实时性处理要求，因此硬件加速方案是合理选择[1,5]。硬件加速是基于专用集成电路（Application Specific Integrated Circuit，ASIC）或现场可编程逻辑门阵列（Field-Programmable Gate Array，FPGA）设计的高速计算电路结构，电路通常采用并行和流水线等特定结构，实现处理任务的高计算速度与高效率运行[2]。

HOUGH变换因计算重复度高、运算量大、模块相对独立且不包含复杂控制序列、动态数组以及动态可变长度循环任务等特点，常用于硬件加速检测线段，可充分发挥硬件并行与流水的优势，且具备极好的鲁棒性与抗干扰性，但当检测非单一线段时，HOUGH变换存在峰值检测最值搜索困难和临近线段干扰真实峰值等问题。根据HOUGH变换算法特点，提出一种适合硬件加速的HOUGH变换检测线段IP实现方案，可检测一帧图像中不含干扰线段的5条共线点最多的线段。

1 算法介绍与难点分析

1.1 算法介绍

HOUGH变换是利用平面点-线变换思想，将笛卡尔坐标系中二值图像的每个特征点通过HOUGH变换转化为极坐标系中的一条曲线，笛卡尔坐标系中共线的点映射到极坐标系中是对应曲线的交点，通过交点获取直线极经ρ与极角θ并结合地址信息完成特殊图像中的临近线段合并，最后通过首末并行有限次扫描获取线段端点。

假设笛卡尔坐标系中直线y=kx+b上有点(x1,y1)，HOUGH变换是将方程参数和变量交换，即将x、y视为已知参数，将k、b视为坐标变量，则直线函数为b=-kx1+y1，为保证k在任意时刻的有效性，将该函数转化为极坐标系下的函数为：

同理，直线上的点(x2,y2)和(x3,y3)映射到极坐标系下为ρ=x2cosθ+y2sinθ和ρ=+x3cosθ+y3sinθ，且 3 条曲线在极坐标系下交于点(ρ0,θ0)，具有相同的极经和极角。可知，笛卡尔坐标系中的点经HOUGH变换映射为极坐标系中的曲线，笛卡尔坐标系中共线的点映射为极坐标系中曲线相交的点。HOUGH变换点-线变换示意如图1所示。

图1 HOUGH变换点-线变换示意图

1.2 硬件实现难点分析

HOUGH算法检测线段实际实现过程中，除了图片大小可配置、数计算复杂度高且计算量大、存储资源需求高以及时间开销大等可通过并行流水线思想解决外，还面临着峰值检测最值搜索困难和临近线段干扰真实峰值等需要优化检测方案或电路结构才能实现的部分，特别是检测任务非单一线段时，以上问题更加尖锐。

峰值检测即需要在累积参数表形成后，找出其中最大的5个有效峰值。由于所需峰值非单一值，峰值问题转化为排序问题，同时累计参数存储在SRAM中，最快只能单周期处理一个数据，不能实现多数据输入电路参与排序，即输入数据带宽低。而且结果要求同时输出多干个可能峰值，若采用常见排序算法，如冒泡排序、堆排序、树状结构排序以及二阶段搜索排序等会多次读取存储器，大大提升时间开销，因此急需一种不重复加载数据、低输入带宽并行输出结果的排序电路。本文提出并行比较电路满足上述要求，排序效率高，结果准确。

虽然HOUGH算法在直线检测时具备极好的鲁棒性，但对于一些特殊图像，如过长过短线段均为待检目标等存在临近线段干扰真实峰值问题，另外由于图像数字化不可避免的偏差，也导致出现虚假峰值，对实际使用形成一定干扰，因此有必要进行类似直线合并。本文通过观察结合理论证明虚假峰值围绕真实峰值呈一定方向出现，根据该特点结合峰值地址判断虚假峰值位置，进而进行类似直线合并得到真实有效5条共线点最多的线段。

2 HOUGH变换硬件实现

硬件实现参数计算部分采用6路并行12路存储计算方案，模块并行度n=12，每输入一个坐标，同时控制三角函数计算CORDIC模块输出15个角度的三角函数值并计算直线参数ρ，特征点计算并存储完成之后再输入下一个特征点坐标值，待所有特征点计算完成后，通过并行比较电路得到累计参数表中最大的14个值，随后去除临近干扰值，得到真实直线对应峰值。根据其地址获取直线参数k、b，最后首末两端同时扫描特征点，得到的第一个满足式（1）的特征点分别对应线段首点和末点，最终检测出一帧图像中共线点最多的5条线段。

2.1 峰值检测模块

峰值检测模块采用两级排序电路，如图2所示，结合参数计算模块，需要将12路存储器整合为6个独立存储bank，第一级6路并行排序搜寻单bank中最大的14个峰值保存在寄存器中，第二级排序电路用于从84个寄存器中搜寻最大的5个峰值为真实直线参数，两级排序电路都采用并行比较排序电路进行搜索。排序单元示意如图3所示。

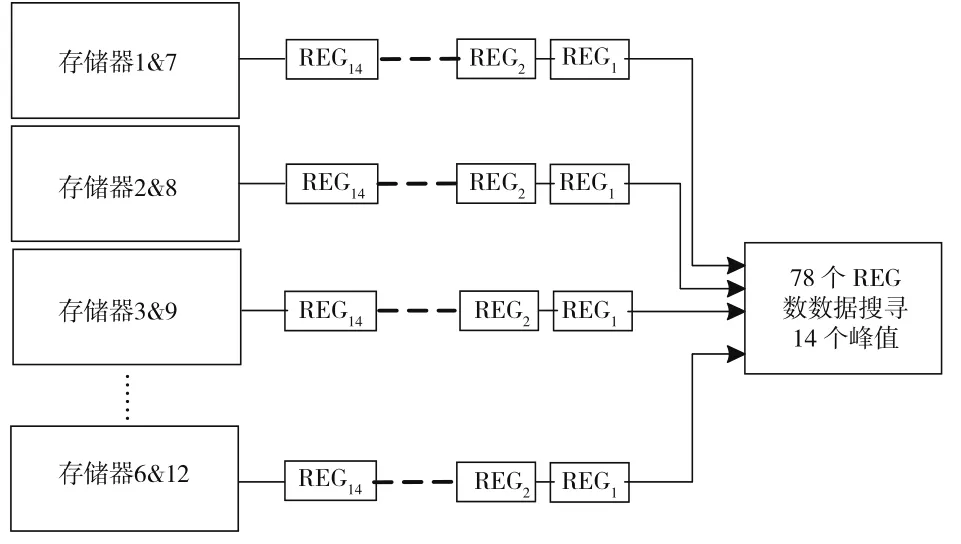
图2 两级排序电路

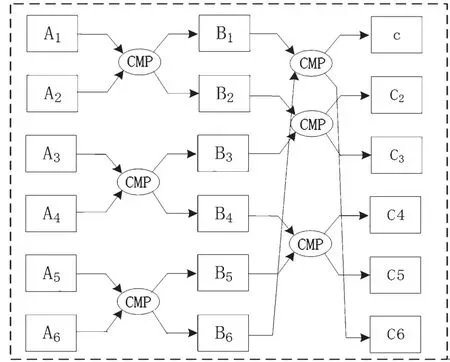
图3 单元示意图

下述以数字1到14的倒序排序介绍本文排序电路结构，倒序排序是时间复杂度和空间复杂度最高的排序，具有一般性。每次运算时数据两两比较，假设所需为降序排序，较大的数据位置上升，较小的数据位置下降，然后奇偶交叉两两比较，升降原则同上，每轮比较奇偶交替，依此类推，这样理论上最多只需要C214次两两比较即可排出正确顺序。同时本文设计的是同步时序电路，为避免时序违例，排序电路3周期完成，详细电路如图4所示，左边为第一个时钟周期内的运算逻辑，中间部分为第二个时钟周期运算逻辑，右边为第三个时钟周期内的运算逻辑。排序完成后输入端数据更新，更新个数可配置，本文为2，依此类推排完所有存储器数据。

图4 并行比较电路简图

本文实测32 760个数据仅需5 564个周期即可完成排序，排序效率，相较二阶段搜索算法提升约60%，相较树状比较电路及冒泡排序、堆排序等在参数累积表中数据不重复加载的前提下，成功实现多值并行排序输出[1]。

2.2 临近线段合并模块

由于计算误差或特殊图像，临近线段干扰不可避免，但通过观察发现所有曲线并非任意方向分布，临近干扰峰值只沿特定角度分布，对θ方向求导所得结果为：

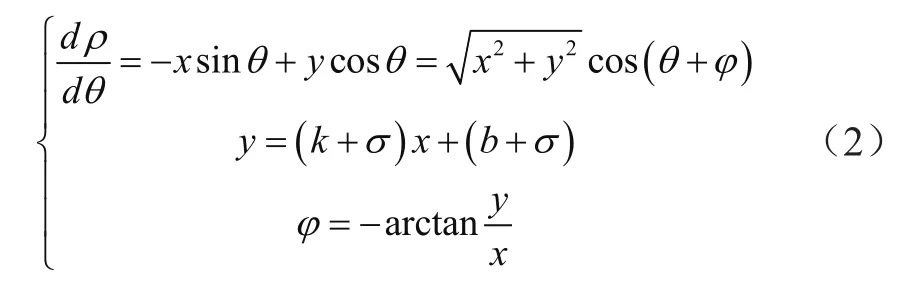
由式（2）可知，ρ的斜率取值范围在之间，所以干扰点一定不会出现在竖直方向，该方向上ρ对θ的斜率为无穷大，同时极坐标系下的交点有θ→θ0，即所有共线点有相同的θ，也就是说在峰值处不会随着θ的变换而变化，而是根据x的改变而改变，对式（2）沿x方向求偏导得：

根据式（3）可知，在峰值点处θ→θ0，为常数，即在峰值点处随x的变化呈一次函数形式变换，ρ在峰值点处随θ的变化是呈二次函数的形式，可知干扰点不会出现在水平方向，因为该方向上ρ不随θ的改变而改变，所以在峰值点只出现在正负45°方向，并且斜率具有单调性，因此为确保正确无误的进行干扰峰值的剔除，需要额外多搜寻出两个点的峰值，最终需要搜寻3×4+1+1=14个峰值点，后续最值地址信息剔除临近线段，剔除效果如图5所示。

图5 剔除效果

3 实验结果

功能验证及上板测试后，实测IP处理一帧64×64像素大小的图像消耗9 901个时钟周期，IP实际运行时钟以150 MHz为例，处理一张64×64像素（特征点占比约为5.4%）大小的图像需要0.066 ms，每秒可以处理约15张64×64像素大小的图片，数据通过率达1.8×107pixel/s，满足系统实时性处理要求，IP处理不同大小图像性能见表1。

表1 IP处理不同大小图像性能

查阅相关资料，将其他学者硬件实现HOUGH变换检测线段IP与本文相比较，由于各个设计面向的应用各有不同，图像大小和测试平台等存在一定差异，下面将从资源消耗、时间开销、数据通过率以及处理性能等角度将本文设计方案与其他学者实现的方案进行对比并做大致评价，结果如表2所示。

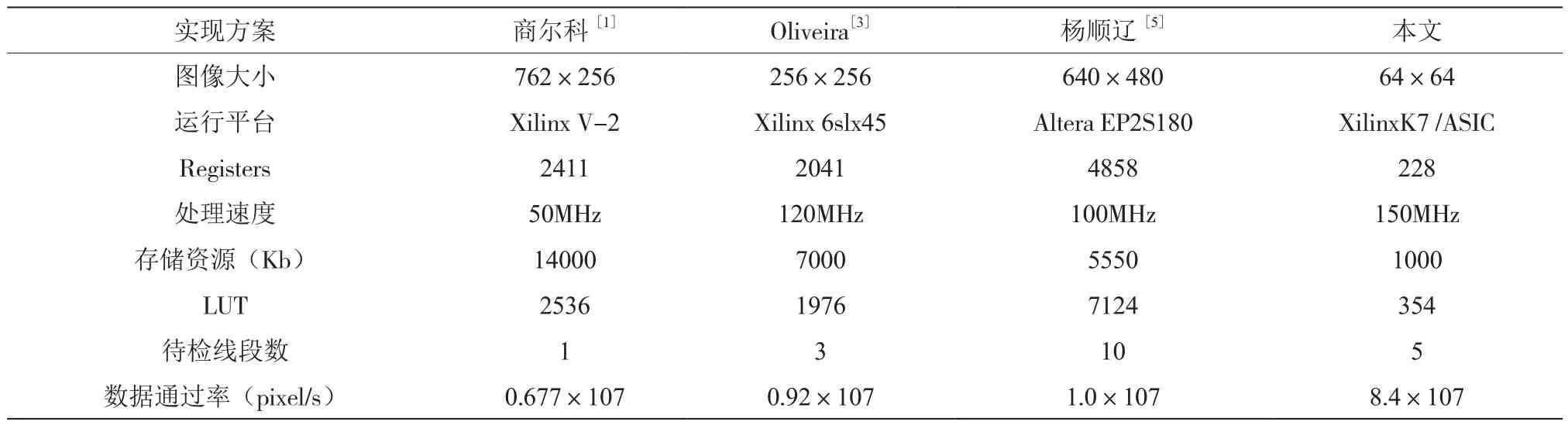
表2 IP性能横向比较

依据表1和表2可知，得益于在峰值检测和端点搜寻等方面的改进，本文设计的HOUGH变换检测线段IP数据通过率最高可达9.58×107 pixel/s，处理性能较其他实现方案有较大提升，在实际项目中可以满足系统实时性处理要求。除此之外，本文在参数计算及存储，模块用6路并行外加少量寄存器达到12路并行的效果，相比其他方案资源消耗有减少约21%。同时本文对临近线段进行合并，剔除真实待求线段附近的误差线段，检测结果更加准确，满足实际使用过程中目标识别的应用要求。