基于赋权TOPSIS与灰色关联分析的风电场电能质量评估模型

张紫雲

（华北电力大学 新能源学院，北京 102200）

0 引 言

21世纪以来，我国风力发电装机容量持续增大，2019年全国风力发电总装机容量4 057×108kW·h，占总发电量的5.54%，风电已经成为中国第3大电力来源。风电在满足能源供给的同时也给电网的稳定性和供电电能质量带来了巨大挑战[1,2]。目前有关不同风电场之间电能质量比较的研究较少，柳永妍依据国家相关标准给出了风电场并网电能质量评估指标及其计算方法[3]。基于此，采用主客观结合赋权的优劣解距离法（Technique for Order Preferenceby Similarity to Ideal Solution，TOPSIS）法结合灰色关联分析，提出了一种针对不同风电场电能质量统一评分的方法。

1 风电场电能质量评价指标

目前对于电能质量我国共有6项国家标准，分别为《电能质量 供电电压偏差》（GB/T 12325—2008）、《电能质量 电力系统频率偏差》（GB/T 15945—2008）、《电能质量 三相电压不平衡》（GB/T 15543—2008）、《电能质量 公用电网谐波》（GB/T 14549—1993）、《电能质量 电压波动和闪变》（GB/T 12326—2008）以及《电能质量 暂时过电压和瞬态过电压》（GB/T 18481—2001）。依据以上标准，将根据电压偏差、频率偏差、三项不平衡度、谐波含量以及电压波动5个指标对风电场的电能质量进行综合评估，各指标的定义如下。

1.1 电压偏差

根据国家标准规定，电压偏差ΔU可以用实际电压U和系统标称电压UN的差值与系统标称电压的百分比来表示，即：

1.2 频率偏差

频率偏差主要是有功功率不平衡导致的，定义如下：

式中，f表示实际频率，fN表示标称频率。

1.3 三相不平衡度

三相不平衡度用电压负序分量均方根与正序分量均方根的百分比来表示，即：

式中，U2代表电压负序分量均方根，U1代表电压正序分量均方根。

1.4 谐波含量

谐波含量用总谐波失真描述，可表述为根号下各次谐波电压的平方比基波电压的平方累加，即：

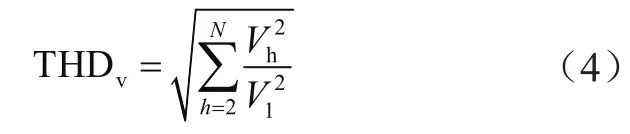
式中，V1为基波电压，Vh为h次谐波电压。

1.5 电压波动

电压波动可表示为电压均方根曲线上两个极值电压Umax与Umin的差值与系统标称电压UN的百分比，即：

2 基于组合赋权的TOPSIS和灰色关联分析

本文改进了传统TOPSIS法，先在原始数据矩阵中加入以国标制定的最优值与最劣值，使每个样本都与最优值和最劣值比较，取各个样本贴近度的平均值作为该风电场的最终得分。TOPSIS法会损失数据信息，而灰色关联分析能较好地依据数据几何形状的相似性反映样本的真实情况[4]。将赋权的TOPSIS与灰色关联分析相组合，以增强评估效果。

2.1 基于赋权的TOPSIS

2.1.1 指标赋权

由于层次分析法存在主观性太强的缺点，而熵权法则是一种客观赋权的方法，因此本文用加权平均将层次分析法和熵权法相结合。

2.1.2 数据矩阵正向化与标准化

文中有关电能质量的指标均为极小型，可采取倒扣逆变换法将指标正向化，公式为：

为消除不同指标间量纲的影响，需要将矩阵标准化处理。记标准化后的矩阵为Z，Z中每一个元素用下式计算：

2.1.3 计算TOPSIS法得分

采用欧氏距离计算各样本的正、负理想距离Di+和Di-，第i个样本的得分为：

2.2 灰色关联分析

对于正向化和标准化处理后的数据矩阵Z，取每一行的最大值构成母序列，计算各指标关于母序列的灰色关联度。则第j个指标的权重Wj可用下式计算：

式中，rj为第j个指标的灰色关联度。

2.3 计算组合得分

引入权重系数α、β计算组合得分S，即：

式中，St为TOPSIS法的得分，Sg为灰色关联分析法的得分。

3 仿真风电场与和平风电场电能质比较

3.1 基于Simulink仿真的算例

利用MATLAB/Simulink平台建立风电场仿真模型，通过模拟双馈异步发电机并网过程中逆变器的交直交转换系统内d-q坐标系下分解后的定转子电压与电流的变化来反映风力机由于风速变化引起的电力变化，在5个风电机组箱变后设置测量节点，得到原始数据如表1所示。

表1 仿真风电场5个节点数据

3.1.1 确定指标权重与原始数据处理

根据AHP层次分析法所得到的主观权重向量W1为[0.42 0.11 0.18 0.17 0.12]，根据熵权法获得的权重向量W2为[0.19 0.26 0.22 0.20 0.13]，本文以8∶2为比例加权平均两种权重得到最终的指标权重向量W为[0.37 0.14 0.20 0.17 0.12]。由此可见，本算例中电压偏差对电能质量影响最大。

3.1.2 计算得分

两种方法的结果见表2，符合定性分析的结果。

表2 两种方法的7个节点得分

两种模型对各节点电能质量排序对比如图1所示，由图可知两种方法对各节点的评价结果基本一致。节点6和节点7分别为最优节点和最劣节点。在灰色关联分析中节点3优于节点4，而在TOPSIS法中则相反。

图1 两种模型对各节点电能质量排序对比

根据式（10）计算组合得分，取α=β=0.5，得到S=0.522 3，该得分可用于跟不同风电场横向对比。

3.2 仿真风电场与和平风电场比较算例

表3为本文引用的和平风电场的测量数据[5]。

表3 和平风电场5个节点数据

计算得到和平风电场最终得分为0.449 6，低于仿真风电场的最终得分0.522 3。由两个风电场的最终得分可知仿真风电场的整体电能质量要优于和平风电场。如图2所示，和平风电场所有节点的电能质量都比仿真风电场差，和平风电场节点4明显优于其他4个节点，而仿真风电场各节点电能质量较平衡，节点1得分略低。

图2 两个风电场各节点得分对比

4 结 论

结合层次分析法和熵权法对影响电能质量的各指标赋权结果表明电压偏差对电能质量影响最大，应该重点降低风力发电机组并网节点的电压偏差。TOPSIS模型的贴近度存在信息丢失的缺陷，通过引入灰色关联分析，充分利用数据的几何信息，组合两种模型得到更准确的评估结果。在原始数据中依据国家标准加入最优样本与最劣样本使得分具有可比性，为多风电场电能质量比较提供了一种解决方法，并在算例中验证了该方法的有效性。