变截面功能梯度Timoshenko梁的自由振动分析
2021-07-01杜运兴程鹏周芬
杜运兴 程鹏 周芬


摘 要:基于梁物理中面的概念,使用哈密顿原理,推导得出轴向力作用下材料性质沿梁高变化的功能梯度材料(FGM)梁自由振动的控制微分方程组,然后求得该微分方程组的幂级数解. 再基于弹性约束表示的一般边界条件得到频率方程. 分析了长高比、梯度指数、轴向力以及截面变化系数等参数对FGM梁固有振动特性的影响. 结果表明,剪切变形不仅会影响弯曲振动,对轴向振动也有影响.
关键词:Timoshenko梁;FGM梁;物理中面;自由振动;幂级数解
中图分类号:O326 文献标志码:A
Abstract:Based on the concept of physical neutral surface, the governing differential equations of free vibration of an axial-loaded functionally graded material (FGM) beam with the material properties varying along the beam height are derived by using Hamilton principle, and then the power series solutions of the differential equations are obtained. Then, the frequency equation is obtained based on the general boundary conditions expressed by elastic constraints. The effects of the parameters such as the length-height ratio, the gradient index, the axial force, and the section variation coefficient on the natural vibration characteristics of functionally graded beams are analyzed. The results show that the shear deformation affects not only the flexural vibration but also the axial vibration.
Key words:Timoshenko beam;FGM beams;physical neutral surface;free vibration;power series solution
随着科学技术的发展,各种高性能材料相继出现,比如功能梯度材料(FGM),FGM是一种微观上不均匀的空间复合材料,通常由两种或多种不同的材料组成. FGM因性能优异而广泛应用于土木、机械和航空航天等领域. 一些学者对FGM[1]或FGM结构[2]进行了研究. 而FGM梁通常作为单独的结构或者作为FGM结构的构件应用于工程中,对于一些受到动荷载作用的FGM梁,求解其固有振动特性从而避免共振具有重要意义. 目前,对于轴力作用下的变截面FGM梁的自由振动问题的研究仍不完善,需深入研究.
对于材料性质沿梁高分布的FGM梁的自振问题已有大量研究. 基于Euler-Bernoulli梁理论,Yang等[3]分析了带有裂缝的FGM梁的自由振动和稳定问题. imek等[4]分析了FGM梁在集中移动简谐荷载作用下的自由和受迫振动. 最近Lee等[5]提出了一种精确传递矩阵法来分析FGM梁的自由振动特性. 尽管基于Euler-Bernoulli梁理论计算较为简单,但是在长细比较小时结果误差较大. 龚云[6]分别基于Euler-Bernoulli梁理论与Timoshenko 梁理论分析了FGM梁自由振动和弯曲问题,结果表明长细比对固有频率影响显著. 基于一阶剪切变形理论,Lee等[7]研究了材料沿截面高度分布的FGM梁的轴向-弯曲耦合振动. 他还分析了FGM梁法向应变能和剪切应变能固有频率贡献率的影响. 该方法能准确地评估剪切变形的影响,蒲育等[8]也提出一种改进型广义微分求积法来求解FGM梁的自由振动问题. 也有一些学者基于高阶梁理论分析该问题,比如,Pradhan等[9]研究了不同边界条件下FGM梁的自由振动问题. 基于不同的剪切变形梁理论以及经典梁理论进行了分析. imek[10]使用不同高阶梁理论对FGM梁的基频进行分析,结果表明使用各种高阶梁理论所得结果差异很小. Karamanli[11]基于三阶剪切变形理论研究了在多种边界条件下,雙向FGM梁的自由振动特性.
上述研究的材料性质沿厚度方向变化的FGM梁均是等截面梁. 对于变截面梁的研究较少. Maganti等[12]分析了FGM旋转楔形梁的弯曲振动,但并未考虑剪切变形的影响. Li等[13]研究了变厚度FGM梁在流体中的自由振动.
对于某些材料性质沿厚度方向变化的FGM梁,其物理中面可能与几何中面不重合. 一些学者[14-16]的研究表明,如果选择合适的参考面即物理中面,就可以消除板振动方程中的拉伸-弯曲耦合,这可以大大减小计算量. 基于物理中面的概念,贾金政等[17]分析了FGM梁的弯曲和过屈曲问题,Larbi等[18]基于高阶梁理论分析了等截面FGM梁的静力和自由振动问题. 但对于轴向力作用下的变截面FGM梁的自由振动问题,还缺乏研究. 因此本文基于物理中面的概念,对于变截面FGM梁自由振动问题进行研究.
在文献[9-10]中,基于高阶剪切变形梁理论所得的结果与基于一阶剪切变形梁理论所得结果差异不大,因此,本文拟基于Timoshenko梁理论对该问题进行研究,并考虑轴向力的作用. 由于变截面FGM梁的自由振动方程为变系数微分方程组,无法用常规方法求解,故本文使用一种幂级数法对该变系数微分方程组进行求解. 通过本文方法容易求得变截面FGM梁的固有频率、振型以及临界荷载,可为变截面FGM梁的设计与应用提供理论支持.
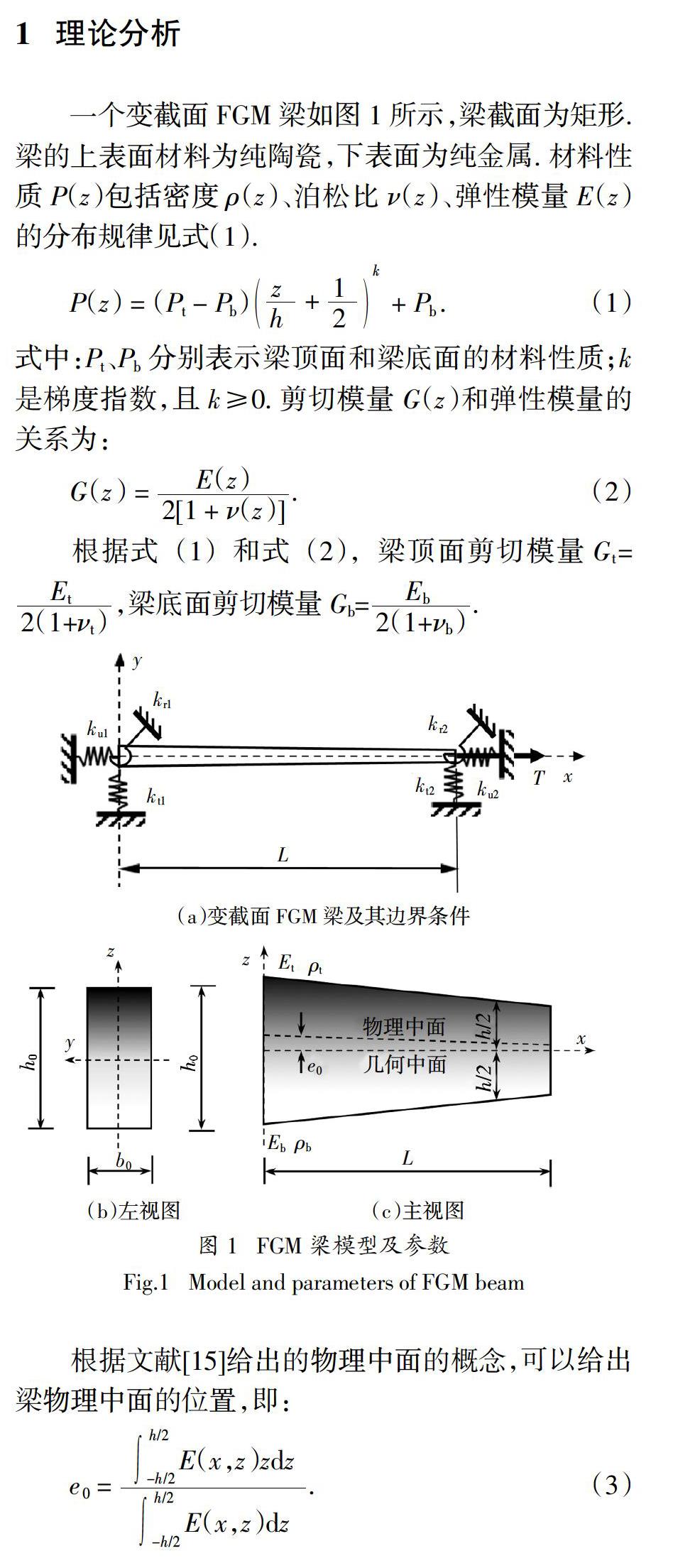
1 理论分析
2 结果与讨论
本文研究的FGM梁的上表面的材料为纯陶瓷(弹性模量为Et = 380 GPa,密度为ρt = 3 960 kg/m3,泊松比为0.3);梁的下表面的材料为纯铝(弹性模量为Eb=70 GPa,密度为ρb=2 702 kg/m3,泊松比为0.3).
2.1 结果验证与分析
由于本文振动微分方程的解为幂级数解,实际计算中经常采用近似解代替级数解,近似解选取级数解前N项计算. 理论上,N越大,无量纲固有频率近似解的精确度越高. 为了探讨近似解所取项数N对无量纲固有频率精度的影响,以文献[10]中的一个等截面简支FGM梁(取α=0来分析等截面梁)为例,梁长与梁高之比1/μ取5和20,梯度指数k取0、1、2,无量纲轴力τ取0. 由表1中的数据可以发现本方法所得的频率方程式(33)的解是收敛的,且近似级数解并不需要取太多项.
计算所得结果与文献[10]中经典边界条件下FGM梁的无量纲基频进行比较,验证了所提出方法的有效性. 且无量纲固有频率随梯度指数k增大而减小. 当长高比较大时所得的无量纲固有频率大于相应的长高比较小时所得的数据,这反映了,长高比较小时,剪切变形对无量纲固有频率的影响较大,不可忽略. 此外,结果还表明:通过调整边界约束弹簧的刚度来求解经典边界条件下FGM梁的固有频率是可行的.
当1/μ取5和10,梯度指数k取1时,简支FGM梁的前四阶振型函数U(X)和W(X)对比如图3所示. 由图可知,梁长与梁高之比对梁的自振特性有显著影响,当 1/μ取5时,第三阶模态由轴向振动主导,而当 1/μ取10时,第四阶模态由轴向振动主导,其他阶模态均由弯曲振动主导. 由于1/μ值的大小反映了剪切变形的影响程度,1/μ值越小,剪切变形影响越大,因此,剪切变形不仅会影响弯曲振动,对轴向振动也有影响.
2.2 截面变化系数对变截面FGM梁自振特性的
影响
使用本文方法计算简支FGM梁无量纲固有频率,取梯度指数k=1,梁长与梁高之比1/μ取100,截面变化系数 α取不同的值时,梁前五阶无量纲固有频率计算值见表2. 由表2中的计算结果可知,随着截面变化系数α增大,梁的无量纲固有频率逐渐减小. 另外,还讨论了截面变化系数α对简支梁前四阶振型函数W(X)的影响,如图4所示,可以看出:随着截面变化系数 α的增大,振型函数W(X)之间的差异逐渐增大. 此外,右端差异较大,这是因为梁截面从左到右端逐渐变小从而使得刚度变小,于是变形就更大,但其形状基本相同.
2.3 轴向荷载对FGM梁自振特性的影响
当轴向荷载作用于简支FGM梁时,其固有振动特性会随轴向荷载的改变而改变,因此,对于轴向荷载作用下的FGM梁需进行进一步研究. 梯度指数k取1,截面变化系数 α取0,梁长与梁高之比1/μ取100. 不同轴向荷载作用下FGM梁的前五阶无量纲固有频率见表3. 由表中数据可以看出:轴向荷载对基频影响较大而对高阶频率影响较小,这是因为当轴向压力快达到临界荷载时,无量纲固有频率才会大幅减小,而轴向压力达到一阶临界荷载时,还远不到二阶临界荷载,因此对高阶频率影响较小. 轴向压力接近一阶临界荷载时,基频会逐渐接近于0.
基于上述结论,在本节进一步分析了对于不同截面变化系数α和梯度指数 k,基频和轴向压力之间的关系,同时分析k和α对FGM梁的临界荷载的影响. 对于简支梁,选择不同的k和α值,梁的基频与轴向载荷之间的关系如图5所示. 从图中可以看出,随着k值的增大,FGM梁的无量纲固有频率都有所减小. 此外,随着k值的增大,临界荷载也大幅减小,这是因为,随着k值的增大,梁中铝的含量增加从而使得梁的弹性模量和密度都减小,而密度的减小对临界荷载没有影响,因此k值的增大会导致一阶临界荷载的减小. 另外截面变化系数α也会导致一阶临界荷载的减小.
3 结 论
本文基于Timoshenko梁理论,建立了变截面FGM梁的自由振动方程,采用幂级数法求解变截面梁振动微分方程组. 随后以上表面为陶瓷、下表面为铝的FGM梁为例,研究了该方法的收敛性,并分析了长高比、梯度指数、截面变化系数以及轴向力对固有振动特性的影响,主要结论如下:
1)本文提出的方法收敛性良好,且具有较高的准确性. 结果表明,剪切变形不仅会影响弯曲振动,对轴向振动也有影响.
2)对于简支功能梯度梁,截面变化系数α和梯度指数 k的增加会使得其固有频率和临界荷载减小,另外,截面变化系数对振型函数也有一定影响,但大致形状不会改变.
3)可以通过改变边界约束弹簧的刚度来实现经典边界条件下梁的固有频率求解.
参考文献
[1] 龙述尧,刘凯远,李光耀. 功能梯度材料中的无网格局部径向点插值法[J]. 湖南大學学报(自然科学版),2007,34(3):41—44.
LONG S Y,LIU K Y,LI G Y. A meshless local radial point interpolation method for the analysis of functionally graded materials[J]. Journal of Hunan University (Natural Sciences),2007,34(3):41—44. (In Chinese)
[2] 杨旭静,胥海波,郑娟. 考虑位移约束的功能梯度结构ICM拓扑优化方法[J]. 湖南大学学报(自然科学版),2017,44(4):56—62.
YANG X J,XU H B,ZHENG J. ICM topology optimization method of functionally graded structures considering displacement constraint[J]. Journal of Hunan University(Natural Sciences),2017, 44(4):56—62. (In Chinese)
[3] YANG J,CHEN Y. Free vibration and buckling analyses of functionally graded beams with edge cracks[J]. Composite Structures,2008,83(1):48—60.
[4] IMEK M,KOCATRK T. Free and forced vibration of a functionally graded beam subjected to a concentrated moving harmonic load[J]. Composite Structures,2009,90(4):465—473.
[5] LEE J W,LEE J Y. Free vibration analysis of functionally graded Bernoulli-Euler beams using an exact transfer matrix expression[J].International Journal of Mechanical Sciences,2017,122:1—17.
[6] 龔云. 功能梯度材料梁弯曲、屈曲和自由振动分析[D]. 兰州:兰州理工大学,2009:9—26.
GONG Y. Analysis of bending,buckling and free vibration of functionally graded materials beam[D]. Lanzhou:Lanzhou University of Technology,2009:9—26. (In Chinese)
[7] LEE J W,LEE J Y. Contribution rates of normal and shear strain energies to the natural frequencies of functionally graded shear deformation beams[J]. Composites Part B:Engineering,2019,159:86—104.
[8] 蒲育,滕兆春. 基于一阶剪切变形理论FGM梁自由振动的改进型GDQ法求解[J]. 振动与冲击,2018,37(16):212—218.
PU Y,TENG Z C. Free vibration of FGM beams based on the first-order shear deformation theory by a modified generalized differential quadrature method[J]. Journal of Vibration and Shock,2018,37(16):212—218. (In Chinese)
[9] PRADHAN K K,CHAKRAVERTY S.Generalized power-law exponent based shear deformation theory for free vibration of functionally graded beams[J].Applied Mathematics and Computation,2015,268:1240—1258.
[10] IMEK M. Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories[J].Nuclear Engineering and Design,2010,240(4):697-705.
[11] KARAMANLI A. Free vibration analysis of two directional functionally graded beams using a third order shear deformation theory[J]. Composite Structures,2018,189:127—136.
[12] MAGANTI N V R,NALLURI M R. Flapwise bending vibration analysis of functionally graded rotating double-tapered beams[J]. International Journal of Mechanical and Materials Engineering,2015,10(1):1—10.
[13] LI H C,KE L L,YANG J,et al. Free vibration of variable thickness FGM beam submerged in fluid[J]. Composite Structures,2020,233:111582.
[14] ABRATE S. Functionally graded plates behave like homogeneous plates[J].Composites Part B:Engineering,2008,39(1):151—158.
[15] ZHANG D G,ZHOU Y H.A theoretical analysis of FGM thin plates based on physical neutral surface[J].Computational Materials Science,2008,44(2):716—720.
[16] SAIDI A R,JOMEHZADEH E. On the analytical approach for the bending/stretching of linearly elastic functionally graded rectangular plates with two opposite edges simply supported[J]. Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2009,223(9):2009—2016.
[17] 賈金政,马连生.纵横载荷作用下功能梯度梁的弯曲和过屈曲[J].应用力学学报,2020,37(1):231—238.
JIA J Z,MA L S.Nonlinear bending and post-buckling of functionally graded beams under transverse and axial loads[J]. Chinese Journal of Applied Mechanics,2020,37(1):231—238. (In Chinese)
[18] LARBI L O,KACI A,HOUARI M S A,et al. An efficient shear deformation beam theory based on neutral surface position for bending and free vibration of functionally graded beams[J]. Mechanics Based Design of Structures and Machines,2013,41(4):421—433.
