跨河桥梁浮式龙门吊主横梁强度计算研究

赵俊达 程志友 卫泽亮 黄荣超

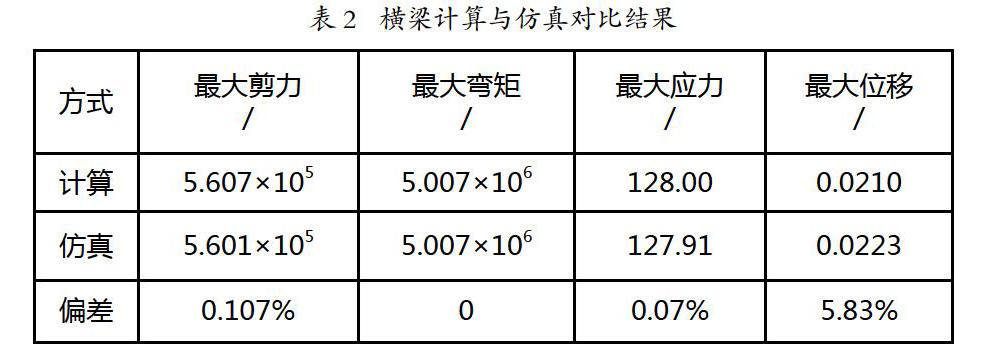
摘 要：以某跨河桥梁浮式龙门吊为对象，在极值工况下运用力学理论计算方法对其主横梁进行强度分析，再利用ANSYS Workbench软件创建主横梁有限元模型，对其进行强度仿真计算。研究结果表明：两种方式计算结果对比，主横梁所受最大应力偏差为0.07%，最大位移偏差为5.83%，最大剪力偏差为0.107%，最大弯矩偏差约为0，偏差相对较小，故有限元分析法可以为浮式龙门吊的整体设计提供基本依据。

关键词：浮式龙门吊;极值工况;主横梁;结构强度;有限元

中图分类号：TH123+.3         文献标识码：A            文章编号：1006—7973（2021）04-0093-03

随着桥梁建设事业的发展，浮式龙门吊的需求迅猛增加，对这一方面的研究也逐步增多。申燚[1]等利用ANSYS软件对浮式起重机横梁进行优化设计以提高结构性能;马晨旭[2]等基于ANSYS对浮式起重机整体结构在不同倾斜角度和加载力下的情况进行仿真计算以得出最佳设计方案;Gerdemeli[3]等研究浮式龙门吊不同荷载组合情况下的数值计算方法，比较了各方法的优缺点;郑惠强等[4]在多因素影响下，使用有限元方法对主、副钩联动作业的巨型浮式起重机进行了完整的设计分析。

1 工程概况

本文研究的跨河桥梁浮式龙门吊采用小浮箱组拼结合双纵横梁龙门吊的形式，主要由基座平台（浮箱、浮箱分配梁、连系梁）、立柱、龙门吊（梁臂）、天车等组成[5]。以某工程实例中的一座跨河桥梁浮式龙门吊为例，设计最大起重量为60t，起吊高度25m。浮式龙门吊主横梁选用空心矩形截面，材料采用Q345B钢。龙门吊所受主要荷载分为：起吊重物，天车及电器电线，横梁的自重均布荷载等[6-7]。

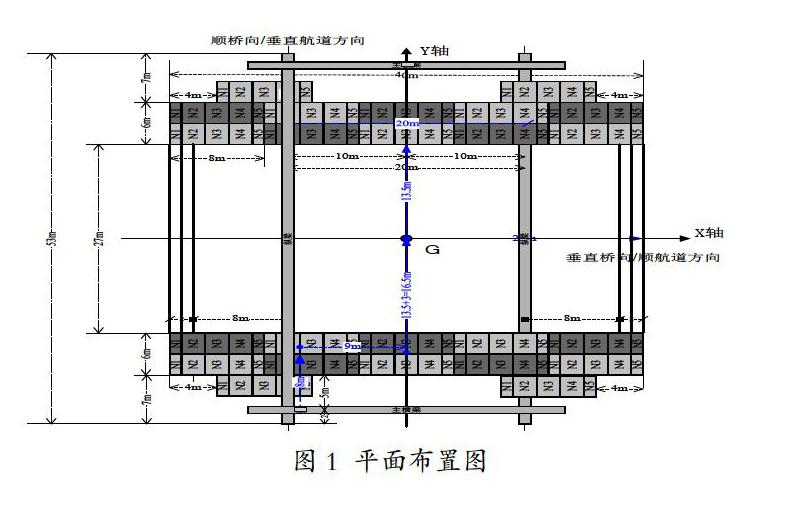
本文中浮式龙门吊具体布置见图1，其主横梁截面见图2。选用的材料相关参数如表1所示。该浮式龙门吊主横梁相关理论计算按简支梁形式作受力分析计算[8]。

2 浮式龙门吊主横梁强度理论计算

2.1 正应力强度校核

2.1.1起吊重物时横梁承受的最大弯矩

（1）

其中为横梁自重均布荷载，为横梁跨距，P为起吊重物和天车及电器电线的合力，为吊点到支点距离。

由（1）得，最大弯矩

2.1.2抗弯截面系数

（2）

则最大弯曲正应力

根据以上计算，能够满足抗弯要求。

2.2切应力强度校核

起吊重物时横梁承受的最大剪力

横梁最大弯曲切应力

根据以上计算，能够满足抗剪要求。

2.3刚度校核

起吊重物时横梁最大挠度

（3）         由公式（3）得

根据以上计算，能够满足刚度要求。

3浮式龙门吊主横梁有限元计算

3.1有限元模型建立

本文采用ANSYS Workbench的梁单元，对浮式龙门吊横梁进行有限元分析[9，10]，步骤如下：

（1）在Static Structural模块中定义材料Q235B钢，在DM模块创建横梁的有限元模型。

（2）对已创建好的横梁有限元模型进行网格划分。设置网格精度为100mm，在受力集中的地方做进一步的局部优化[10]，结果如图3所示。

（3）施加边界条件。选取横梁的最左端，施加简支约束，限制三个平动自由度，两个转动自由度;最右端施加一个可沿轴向移动的约束;在整段梁上加载均布荷载;在横梁中点处加载一个集中力，如图4所示。

（4）计算结果。图5中分别为横梁受力的弯矩剪力图以及挠曲线。

由图5可知，横梁所受剪力最大值出现在两端支点，最大值取5.601e5N，离中点越近剪力越小，最小值为4.413e5N;横梁所受弯矩最大值出现在跨中，最大值取5.007e6N·m，越向两端延伸弯矩越小，近似为0。

图6中横梁位移最大值出现在跨中，最大值取0.022322m，小于横梁的许用挠度0.04m，故横梁变形在允许范围内。

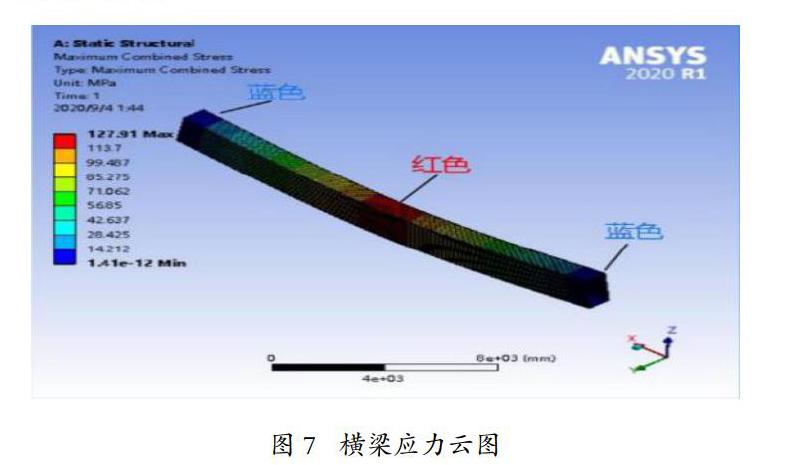
图7中横梁所受最大应力出现在跨中，为127.91MPa，未超过横梁许用应力170MPa，从中间到两端逐渐减小，最小近似为0。故该工况下横梁最容易在此处出现断裂，即危险截面出现在跨中。

3.2 结果对比分析

（1）浮式龙门吊主横梁选用的材料Q235B满足设计要求;

（2）理论计算与有限元仿真得到的强度、刚度和位移等结果对比显示，最大剪力偏差为0.107%，最大弯矩偏差近似为0，最大应力偏差为0.07%，最大位移偏差为5.83%，偏差较小，故有限元分析法可以为浮式龙门吊的整体设计提供可靠参考。

4结语

本文运用理论计算和有限元软件仿真对跨河桥梁浮式龙门吊主横梁强度进行分析，为类似设计的强度计算提供了参考。主要结论有：

（1）龙门吊主横梁危险截面出现在跨中位置，最大剪力发生在两端支点处;最大弯矩发生在跨中处;最大应力发生在跨中处;最大位移发生在跨中处。

（2）浮式龙门吊在起吊重物时，通过理论计算和Ansys workbench仿真的结果几乎一致，满足强度条件，验证了结果的正确性和整体设计的可行性;

（3）理论计算对参数要求相对保守，结构余量较大。有限元仿真可根据需要建立较真实的模型，对结构的计算更接近真实情况，更容易获得结构各部位的应力应变情况。

参考文献：

[1]申燚，张盼盼，李鸣，等.基于ANSYS的4500T浮式起重机主梁结构优化设计[J].机械设计，2017，34（02）：73-77.

[2]马晨旭，霍焰，朱磊，等.不同加载方式下的200t浮式起重机有限元分析.起重运输机械，2020（5）.

[3]Gerdemeli I ， Akgun G ，Kurt S . DESIGN AND ANALYSIS WITH NUMERICAL METHOD OF GANTRY CRANE MAIN BEAM[C]// International Conference on Innovative Technologies. 2013.

[4]鄭惠强，申静静，张氢.7000t浮式起重机臂架钢结构分析[J].中国工程机械学报，2008（02）：184-187.

[5]文艳，张云峰，崔桂媛，等.大型浮式平台结构强度[J].中国海洋平台，2019，34（05）：37-40.

[6]GB/T 3811-1983. 起重机设计规范[S]. 1983.

[7]张质文，王金诺.起重机设计手册[M].北京：中国铁道出版社，1998.

[8]曾传胜.轻型龙门架几种校核方法的探讨[J].科学时代，2013，（6）.

[9]王佳怡. 基于ANSYS Workbench的简式汽车起重机优化设计[D].延边大学，2013.

[10]王雪峰. 电动葫芦门式起重机结构分析与优化设计[D].郑州大学，2014.