基于改进前推回代的含分布式电源配电网潮流计算方法

陈慧娜，杨 军，高梦妍，赵 通，李依霖

（北京石油化工学院 电气工程及其自动化系，北京102600）

分布式电源以其清洁低碳、灵活高效等特点得到广泛的应用。典型的分布式电源类型主要包括分布式光伏、风力发电、太阳能光伏发电、燃料电池和微型燃气轮机等。

分布式电源的接入使配电网成为多电源网络，改变了配电网的结构。分布式电源多种多样，接入不同的分布式电源类型也会影响电力结构中配电网系统的网损值和电压的稳定[1]。因此，我们要对不同类型的分布式电源进行建模，而潮流计算是对其影响进行量化并能得到修改的主要分析手段，如果进行正确的含分布式电源的潮流计算，就能够对电网进行准确的评估，从而优化电网运行，将对电网的影响力降低，并对电网进行优化和完善。

前推回代算法是对辐射型配电网络进行潮流计算的有效算法，由于其编程简单、计算效率高，广泛应用在配电网潮流计算中，针对分布式电源接入对配电网的影响，需要对其进行改进。在前推回代算法改进中，国内外不少学者为此都提出了自己的一些见解。文献[2]针对传统的前推回代算法做出了一些改进措施，提高了潮流计算的运算速度；文献[3]提高了对功率要求的准确度；文献[4-6]考虑了其负荷的电压静态特性，完善了其实际应用性对电压的要求，但是配电网在运行过程中稳定性降低了，而本文通过公式转变了接入节点的类型不仅提高了配电网运行过程中的稳定性，而且还降低了电网损耗。

本文通过对4 种不同类型的分布式电源模型建模分析，针对接入10 kV 配电网的场景，分别设计其潮流计算方法，并使用IEEE33 节点模型基于Matlab 进行仿真验证。

1 分布式电源在潮流计算中的模型

1.1 分布式电源模型

1.1.1 风力发电

风力发电技术是将风能转化为电能的发电技术。风力发电干净无污染、安全性能好，而且它是一种新颖的可再生新能源，目前分布式风力发电技术在我国已经得到广泛的应用。风力发电机不仅有同步发电机还有异步发电机，从对风力发电机的研究得知，异步发电机为其主流方式，而且异步发电机的特性是其无功功率需要系统对它提供。风电机组的无功功率大小可以由公式Q=Ptan φ 确定，φ 为风电机组的功率因数，功率因数可以由并联电容的大小来改变。功率因数的要求是需要大于0.9，即cosφ>0.9，且φ<0。在此无功功率的大小不仅由功率因数决定，而且还与其控制类型有关[3]。本文在恒功率因数控制方式下，把风电机组节点当作是PQ节点；在恒电压控制方式下，将风电机组节点当作是PV节点处理。

1.1.2 光伏发电

光伏电池是一种使吸收太阳能转化为电能的发电装置。它输出的是直流电，与电网连接时通常需要通过逆变器来变为交流电并进行升压来接入更高压的电网中[7]。通常情况下，配电网利用的是光伏发电的有功功率，然而在一些特定的情况下，可以损失一部分输出的有功功率来控制逆变器对配电系统进行无功优化[8-9]，使得电网运行更加经济和稳定。其输出有功和无功功率以及电流的关系为

式中：e是并网电压实部；I是注入电流；f是并网电压虚部；P为输出有功数值。在潮流计算中，将利用光伏的分布式电源的潮流计算当作PI节点处理。也就是将这次求得电压的实部与虚部引入公式，使得无功值得以确定。

1.1.3 燃料电池

燃料电池是一种把燃料所具有的化学能转化成电能的装置，这类生物质能的消耗往往不会对生态环境造成影响，污染程度低。燃料电池的输出功率受电池内气体的浓度影响，其输出电压受逆变器参量控制，类似普通发电机功率调节原理，因此在潮流计算中把燃料电池当做PV节点处理[4]。

1.1.4 微型燃气轮机

微型燃气轮机是一种能够将热能转化成为机械能的一种发电装置，它的转速很高，可达到80000 r/min，而且交流发电机具有很高的频率。在新能源发电领域目前还处于高水平。由于其采用燃料为原料，而且由于其输出功率与其中的燃料量成正比，所以微型燃气轮机的输出功率是可以人工改变的。通过利用燃气轮机不仅能改善生态环境，还能提供电力资源的发电方式成功并入电网系统，燃气轮机接入电力网有两种方式，一种是通过电压控制逆变器接入电网，另一种是通过电流逆变器接入电网。通过电压控制逆变器接入电网的微型燃气轮可以处理为PV节点，而通过电流控制逆变器接入电网的微型燃气轮机可以处理为PI节点。

1.2 节点类型分析

1.2.1PQ恒定型分布式电源

如果DG并入电网时，其运行水平不超过额定的范围，那么进行含DG的潮流计算就可将其作为PQ节点。作为PQ节点进行运算时，输出有功和无功的数值变化趋于稳定。基于这种特性最为常见的绿色能源的分布式电源-风电，就可当作PQ节点进行分析。将其当作方向相反，但功率大小相同的负荷来进行对PQ恒定型DG的分析。可以得出视在功率为S=P+jQ，即得到如下公式：

式中：e为分布式电源电压的实部；f为分布式电源电压的虚部。通过公式（2）将PQ恒定型分布式电源模拟为注入电流。

1.2.2PI恒定型分布式电源

光伏发电系统引入逆变器后，有功和注入的电流便是恒定不变的，对于这种PI恒定型的分布式电源，首先通过式（1）求出无功功率，通过式（2）的处理就可把这类节点当作PQ节点。

1.2.3PV恒定型分布式电源

PV恒定型的分布式电源在如微型燃气轮机等，出现修正后的无功功率超出要求范围的这种情况时，处理方法改为向PV节点注入补偿电流，将这时的PV节点当作PQ节点来处理，电流值为

式中：Zii是PV节点的自阻抗，数值其实就是节点i到根节点上各个支路阻抗的阻抗和；是指对应节点电压幅值前后的改变量；是指注入补偿电流的相量。

1.2.4PQ（V）分布式电源

当对DG进行分析时，对发出有功功率是固定不变的值，无功功率的变化取决于机端电压的改变，也就是一种P恒定，V不定，而Q又是受P，Q限定的节点称之为PQ（V）型节点。

每次迭代进行修正电压完成对PQ（V）节点处理，利用式（1）计算得出系统吸收的无功功率，计算流程为首次迭代将PQ（V）暂时当作成PQ节点（便于使用传统算法计算）；再利用式（2）将PQ（V）型的DG模拟成注入电流计算。第二次迭代，利用修正电压已知的条件计算无功，此时再次当作PQ节点，不断重复，直至迭代收敛。

2 改进前推回代方法

2.1 前推回代法

该算法的原理是首先假设此时配电网中的根节点电压数值与系统中每个节点的电压均相同；再依据网络中末端节点的功率，前推得到始端功率支路电流；再根据这些已知的条件，这次由首端起向末端进行求值，以获得每个节点的电压。重复该流程以保证每个节点的电压差符合要求为止[7]，前推回代法以其简单、灵活、速度快、收敛性好脱颖而出，辐射状配电网如图1所示。

图1 辐射状配电支路图Fig.1 Radial distribution branch circuit diagram

前推回代法的计算流程如下：

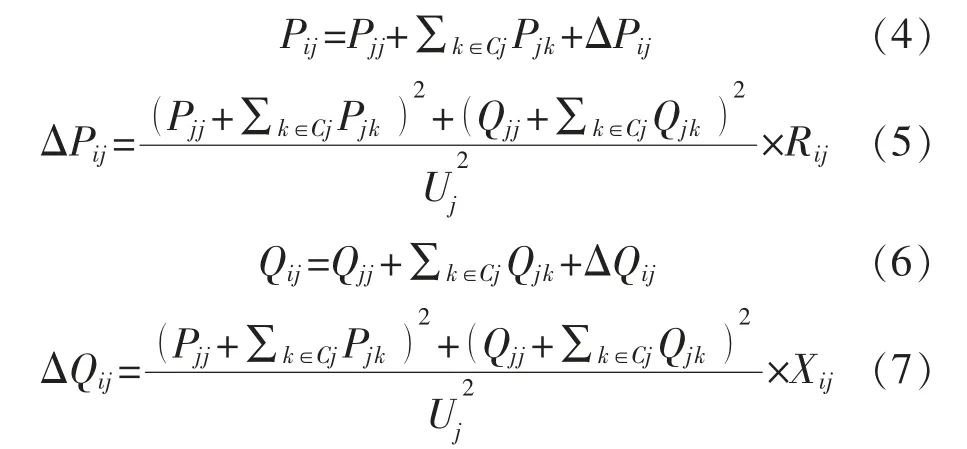
公式（5）表示，任意支路的末端电压幅值与该支路的始端功率呈一定的相关性。

由于分布式电源的引入，使配电网形成环网与PV节点，需要对前推回代法进行改进才能适应分布式电源的影响。

2.2 改进前推回代方法

2.2.1 不同节点类型的模拟方法

不同节点类型的模拟方法如表1所示。

表1 不同节点类型的模拟方法Tab.1 Simulation methods of different node types

2.2.2 含分布式电源配电网潮流计算步骤

步骤1正确选取并获得解环点信息，形成PV节点所对应的入端阻抗矩阵和导纳、解环端口的矩阵。然后对系统进行初始化进程，使得PV节点所对应的叠加电压ΔV和解环端口的开路电压V都为0，令各节点的电压均为根节点电压值。

步骤2求取节点注入电流。对于PV节点注入电流求解公式如式（3）；对于PQ节点注入电流求解公式如式（2）；求解有关PQ（V）节点注入电流需2 个过程，第一利用公式（7）将PQ（V）节点转换成PQ节点，再依靠上文提出PQ节点求取过程进而获得PQ（V）节点注入电流；求解有关PI节点注入电流的求取过程分为2 个步骤，首先利用公式（1）将PI节点转成PQ节点，再利用上文PQ节点求解的方法进行求取。

步骤3修正支路电流。对解环端口的电流补偿值进行准确计算，此时配电网形状发生变化，由少环转换成纯辐射状。

步骤4更新各支路无功功率，利用以求得的注入电流对其进行更新，再前推各支路功率，最后回代求节点电压[10]。

步骤5对于特殊PV节点处理。若无功功率达到边界值，则把PV节点变为PQ节点计算；若注入电流达到边界值，则把PV节点变为PI节点进行迭代。

步骤6对收敛与否进行判断[11]，依据电压设定值与潮流计算获取的电压间的差值maxΔV<ε，判断是否达到收敛精度要求且具备收敛性。若不收敛则重复步骤2 继续进行迭代。潮流计算流程如图2所示。

图2 潮流计算流程图Fig.2 Flow chart of power flow calculation

3 Matlab 验证仿真

3.1 仿真模型及参数设置

选用的算例是IEEE33 节点所对应的配电系统。图中描述了网络接线的具体情况，网络总负荷大小为5084.26+j2547.32 kVA，配电系统网络接线图如图3所示。

图3 配电系统网络接线图Fig.3 Network wiring diagram of power distribution system

该算例有支路32 条，环路5 条以及1 个电源网络首端基准电压12.66 kV、三相功率准值取1 MVA，各节点支路间的负荷以及阻抗如表2所示。

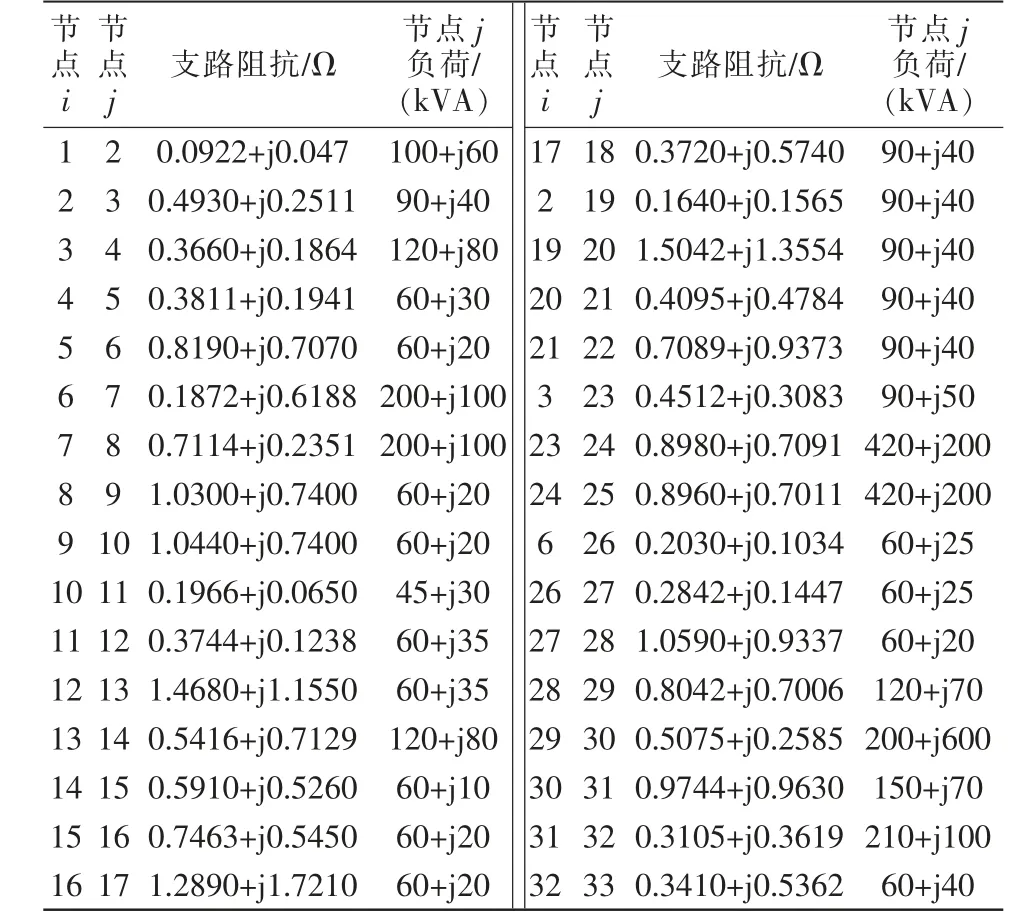
表2 各节点支路间的负荷以及阻抗Tab.2 Load and impedance between branches of each node

3.2 仿真结果分析

3.2.1 同类型不同节点的分析

将DG接入的类型统一设定为PQ节点，观察接入到不同节点后该模型节点电压的变化程度，方案及运行结果如表3所示。

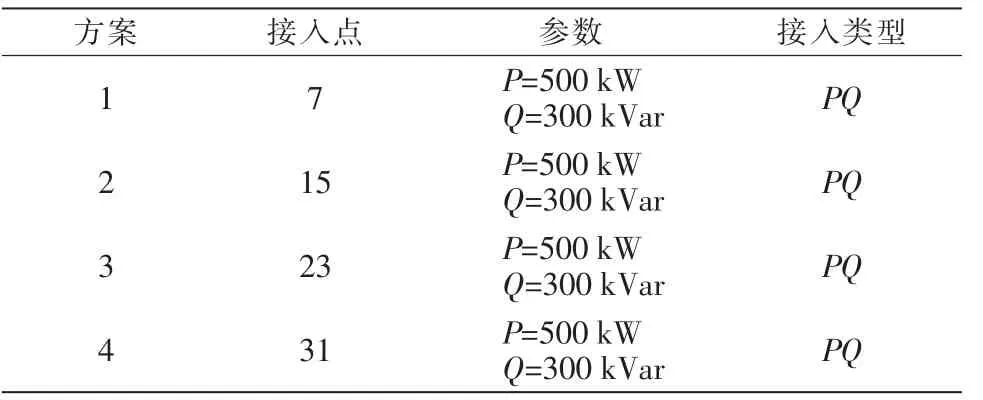
表3 同类型不同接入节点方案及运行结果Tab.3 Different access node solutions of the same type

4 种不同接入节点方案和在不加分布式电源这5 种情况分别在Matlab 进行仿真的节点电压幅值如图4所示。

图4 同类型不同接入节点运行结果Fig.4 Operation results of different access nodes of the same type

方案1：与未加分布式电源相比，有功损耗为150.74 kW，无功损耗为98.928 kVar，系统的最低电压为0.92589 kV。

方案2：与未加分布式电源相比，有功损耗为133.69 kW，无功损耗为88.309 kVar，系统的最低电压为0.92756 kV。

方案3：与未加分布式电源相比，有功损耗为182.13 kW，无功损耗为124.06 kVar，系统的最低电压为0.91599 kV。

方案4：与未加分布式电源相比，有功损耗为129.05 kW，无功损耗为85.952 kVar，系统的最低电压为0.92441 kV。

3.2.2 同一节点不同类型分析

为了方便得出结论，我们所以选择节点18 作为接入的节点，观察不同DG类型接入后的电压变化及对应不同方案产生的电压变化，如表4所示。

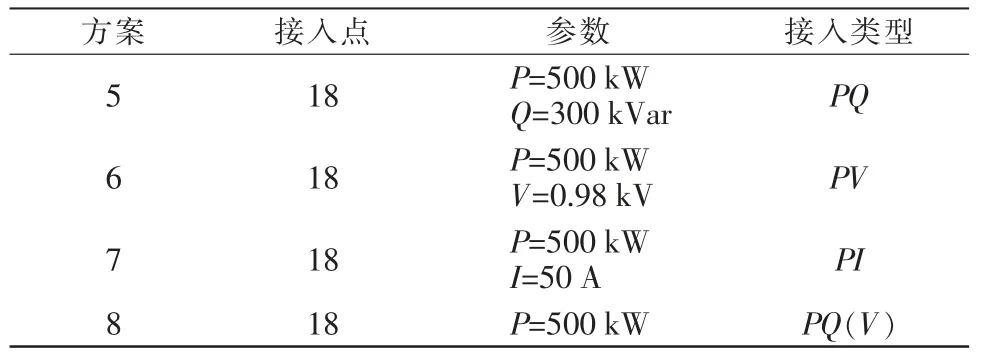
表4 同一节点不同类型方案Tab.4 Different types of schemes on the same node

4 种不同DG类型接入方案和在不加分布式电源这5 种情况分别在Matlab 进行仿真的节点电压幅值如图5所示。

方案5：与未加分布式电源相比，有功损耗为136.23 kW，无功损耗为91.39 kVar，系统的最低电压为0.9275 kV。

方案6：与未加分布式电源相比，有功损耗为132.87 kW，无功损耗为90.867 kVar，系统的最低电压为0.92944 kV。

方案7：与未加分布式电源相比，有功损耗为134.65 kW，无功损耗为90.694 kVar，系统的最低电压为0.92804 kV。

方案8：与未加分布式电源相比，有功损耗为176.95 kW，无功损耗为119.51 kVar，系统的最低电压为0.92195 kV。

3.2.3 相同节点、同类型分布式电源其他情况的分析

假设DG接入节点为节点18，DG接入的类型为不变的PQ节点类型。观察其在不同参数情况下的节点电压及网损情况，如表5所示。

表5 相同节点、同类型分布式电源其他情况方案Tab.5 Same node，same type of distributed power supply，other scenarios

4 种不同功率输入方案和在不加分布式电源这5 种情况分别在Matlab 进行仿真的节点电压幅值如图6所示。

图6 相同节点、同类型分布式电源其他情况运行结果Fig.6 Operation results of same node and same type of distributed power sources in other conditions

方案9：与未加分布式电源相比，有功损耗为161.79 kW，无功损耗为106.98 kVar，系统的最低电压为0.9221 kV。

方案10：与未加分布式电源相比，有功损耗为136.23 kW，无功损耗为91.39 kVar，系统的最低电压为0.9275 kV。

方案11：与未加分布式电源相比，有功损耗为123.64 kW，无功损耗为86.459 kVar，系统的最低电压为0.93252 kV。

方案12：与未加分布式电源相比，有功损耗为122.28 kW，无功损耗为89.721 kVar，系统的最低电压为0.93641 kV。

由此可以得出，增加多种分布式电源发电，配电网系统有功损耗和无功损耗可以明显降低，各节点电压的也得到了提高。

4 结语

面对当前能源供应紧缺和电力故障等问题，减小电网损失，稳定电压和电力系统中配电网运行结构进行优化和完善是其潮流计算的研究方向。根据分布式电源接入特点，分布式电源技术的发展主要集中在以下两方面：一是更精确的分布式电源模型的接入和建立，二是不断完善潮流计算算法，使之能准确智能地为配电网系统服务。