挖知识源流，助文化互融——以基于数学史的“三角形的面积”教学为例

□ 刘树霞 郑玲玲

一、引言

对数学文化的关注肇始于数学界对数学与文化关系的讨论，数学文化进入数学教育领域引发了“数学文化热”思潮，进而促进了数学学科自身的科学价值与人文价值的融合，对中国数学教育教学改革具有重要的启蒙意义。[1]目前，很多教师借助基于数学史的数学文化进行教学，以期让学生感受数学的科学价值、应用价值、审美价值和文化价值。但基于数学史的数学文化的教学绝非易事，因为这不仅要关注数学发展的历史，更要符合学生的认知基础和认知规律[2]，同时教材的内容编排并未重视历史脉络的显性呈现或隐性渗透。笔者以“三角形的面积”为例，介绍基于数学史的数学文化教学实践。

二、历史材料及其运用

三角形的面积计算公式，自古埃及开始经历了漫长的发展和演变过程，表1呈现了不同时空中与三角形面积计算有关的历史素材。

表1 历史上三角形的面积计算方法

续表

在小学教材里，三角形面积公式的推导方法主要包括倍拼法和割补法，国内的教材大部分以倍拼法为主，但是在转化方法的地位上看，这两种方法并没有主次之分。[3]以欧氏几何为代表的演绎几何体系符合学生的认知基础和发展规律（我国的教材编排深受这种传统思想的影响，进而影响到学生的思维方式），但从学生的长远发展与文化的角度看，将割补法放到与倍拼法同等的位置，甚至更高的位置是必要的。一方面，相比于倍拼法，割补法的应用更为广泛，初高中有大量的相关课题；另一方面，割补法背后的出入相补思想是中国古代数学的重要原理，将其融入教学有助于学生感受中国的数学传统、文化传统。

因此，在“三角形的面积”教学中，我们重视学生对割补法的探究，试图将史料中刘徽的方法、欧几里得的结论以及面积的起源融入教学，其他方法作为“意外惊喜”，以期从“知识源流”（指某个知识点的历史演进过程中所涉及的人物与事件、概念与术语、问题与求解、命题与证明等）、“学科联系”（指数学与其他学科之间的关联）、“社会角色”（指数学在人类生活、科学技术、社会发展中的贡献和意义）、“审美娱乐”（指数学美，包括对称美、奇异美、简洁美、统一美等，以及趣味数学）、“多元文化”（指不同文明、不同地域的数学家在同一数学课题上的贡献与意义，以及与数学相关的人文活动）[4]这五个维度体现数学的科学价值、应用价值、审美价值、文化价值。

三、教学设计与实施

（一）追根溯源，直击问题

师：有句话说得好，足不出户就可以观世界。今天，我们就穿越时光来到古老的埃及。在这里，人们靠着尼罗河冲刷出的土地种植庄稼。但尼罗河的河水年年都会泛滥，所以每年人们都面临同样的问题——重新丈量土地、进行公平划分，因此，古埃及的人们开始了对面积的研究。现在就有这样两块土地（如图1），它们的面积分别是多少？要想知道它们的面积，需要测量什么？

图1

平行四边形的面积计算学生已知，学生猜测要计算三角形的面积需要测量底和高或三边的长度。

师：计算三角形的面积到底应该测量什么？又该如何计算呢？这节课我们就一起来研究。

（二）自主探究，构建模型

1.探究直角三角形的面积

师生一起回忆平行四边形面积的推导方法后，教师开始引导学生经历以下思考。

师：研究三角形的面积可不可以也借助转化思想呢？该怎样转化？转化成什么图形？先想一想，三角形按角分，可以分成什么？

生：直角三角形、锐角三角形和钝角三角形。

师：你们打算先研究哪种三角形的面积？

生：直角三角形，因为它有直角，更容易转化成长方形。

师：你们的想法和古代数学家的竟然不谋而合，很多数学家也是从直角三角形入手研究的……这就是数学研究中常用的方法，从特殊到一般。下面我们就先研究直角三角形的面积。

课件出示探究要求，学生探究后汇报交流，表2 呈现了学生探究出的方法以及学生在教师引导下进行方法对比的成果。

表2 割补法和倍拼法的对比

2.探究一般三角形的面积

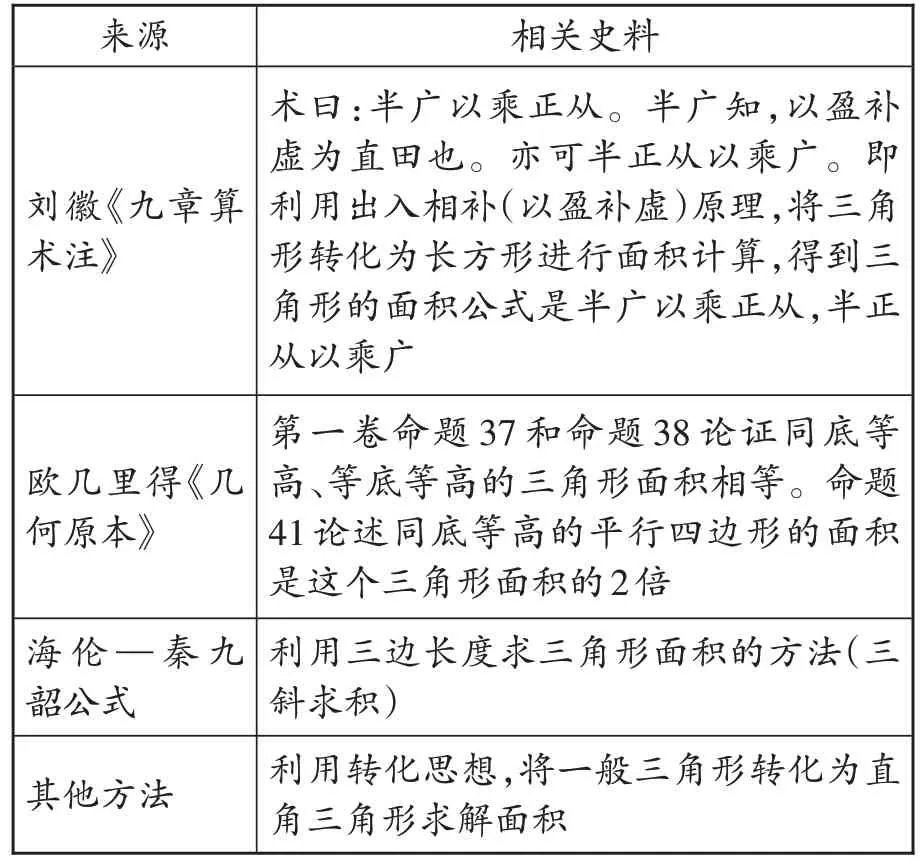
引导学生借助直角三角形面积的研究经验，探究锐角三角形和钝角三角形的面积公式。

学生分别用割补法和倍拼法求出锐角三角形和钝角三角形的面积计算公式，发现公式也是底×高÷2。

师：刚才我们用了割补法和倍拼法研究出了锐角和钝角三角形的面积公式，除此之外，还有其他方法吗？大家请看这种方法（出示图2），我们可将锐角三角形或钝角三角形转化为直角三角形来进行计算。

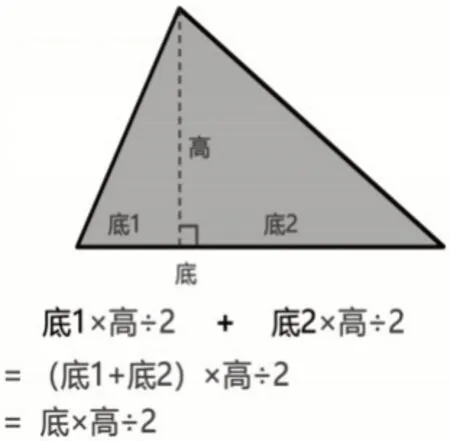
图2

……

师：通过以上研究，我们得出直角三角形、锐角三角形和钝角三角形的面积公式都是底×高÷2，所以，我们就可以说任意一个三角形的面积计算公式都是底×高÷2。如果用S 表示三角形面积，a 表示底，h表示高，面积公式如何用字母表示？（生答）

3.古今方法贯通

师：三角形的面积公式已经研究出来了，我们带着这个公式重新回到古埃及来解决土地问题，现在知道计算三角形的面积需要测量什么了吗？

生：底和高。

师（指图1）：当我们解决了三角形面积计算的问题后，再来观察这里的三角形和平行四边形，你发现了什么？

生：三角形和平行四边形的底和高一样长。

生：三角形的面积是平行四边形面积的一半。

师：你们不仅会推理更会观察。在2300 多年前，古希腊伟大的数学家欧几里得也有与大家相似的结论“三角形的面积是与它等底等高的平行四边形面积的一半”。西方的欧几里得被誉为“几何之父”，中国有一位被称为“中国的欧几里得”的数学家，知道是谁吗？他就是我国伟大的数学家刘徽。他在数学名著《九章算术注》中记载了三角形面积的计算方法，大家看（师出示图3），这种方法我们称为割补法，它是用了哪种方式呢？

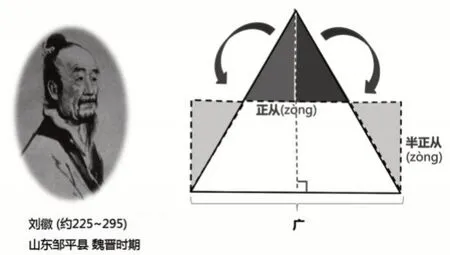
图3

生：半高。

师：古代把底叫作广，把高叫作正从，那这个半高也就是半正从，刘徽推导出的三角形面积公式是什么呢？

生：正从÷2×广。

师：正从÷2也就是半正从。公式还可以写成：半正从×广。同样的道理，他还用半底法得出了公式：正从×半广，在这个方法里刘徽将多的部分称为盈或者出，而补充的部分叫作虚或者入，所以这个方法也叫作“以盈补虚法”或者“出入相补法”。其实“以盈补虚法”或者“出入相补法”的原理就是我们今天用到的转化思想。

4.拓展提升，余味课外

师：计算三角形的面积需要知道什么？

生：底和高。

师：必须知道底和高吗？

生：必须。

（教师介绍海伦—秦九韶的方法，如图4）

图4

师：计算三角形的面积必须知道底和高吗？

生：不是必须的。

师：对，同学们，条条道路通罗马，解决问题的方法也不止一种，有时候我们换种角度可能会有不一样的发现。这就是研究和思考带给我们的成长。

四、结语

基于数学史的数学文化教学，以数学史的梳理为基础，以数学史文化内涵的挖掘和教学应用为重点。与“三角形的面积”相关的史料丰富，涉及古埃及、古希腊、古代中国的数学成就。这些数学史料涵盖了“知识源流”——比较清楚地记述了三角形面积的认知历史；“社会角色”——反映了数学的使用价值，数学起源于农业生产，被用于土地的分配；“审美娱乐”——尽管三角形的面积推导有两种方法，但背后的数学思想都是转化，体现了数学的统一美；“多元文化”——虽然三角形的面积推导都应用了转化思想，但以古希腊为代表的西方数学和以古代中国为代表的东方数学在面积推导过程中表现出了不同的特点，展示了不同的文化特征。

在教学应用中，我们基于对数学文化特征的深度挖掘，结合学生的认知发展规律，进而重构了知识的发生发展过程。以几何学的起源为开端，顺应式地融入了古希腊等底等高的三角形与平行四边形面积关系的命题；借助“由特殊到一般”的研究策略，从直角三角形的面积探究到锐角、钝角三角形面积的探究，较为自然地探究出了割补的方法、倍拼的方法，特别是探究出了将三角形割补为平行四边形的方法；在古今对照中，了解了古人的方法，增强了数学学习的自信心，拓展了知识面，原来也可由三边长度得到三角形的面积。

基于数学史的数学文化教学要以教学目标的达成为指向。学生在三角形面积计算的发展历程中感受到了知识之谐；在面积推导的过程中，探究出了多种方法，体验了探究之乐，感受了方法之美；掌握了面积推导的多种方法，发展了几何直观能力、逻辑推理能力等关键能力；在古今中外方法的对比中，认识到了数学是不同国家、不同民族共同创造的结果；在问题引领、合作探究的过程中，激发了好奇心与求知欲，提升了自信心。

奥地利物理学家、哲学家恩斯特·马赫（Ernst Mach，1838—1916）曾说过：没有任何科学教育可以不重视科学的历史与哲学。哲学家培根说，读史使人明智。数学史不只是人物和事件串联成的故事，更是这些故事背后的数学问题、数学思想、数学方法和精神。基于数学史的数学文化教学让我们体会到了历史与现实、数学与人文的沟通，学生在课堂中穿越时空，了解古今中外数学家的思想方法，树立了文化自信和理论自信。