基于GA-RBF神经网络的位山闸引水能力预测研究

2021-07-01李守涛王军涛于明姚京威赵国平樊玉苗

灌溉排水学报 2021年6期

李守涛，王军涛，于明，姚京威，赵国平，樊玉苗

（1.黄河水利科学研究院，郑州 450045；2.河海大学水利水电学院，南京 210098；3.聊城市位山灌区管理处，山东聊城 252053；4.聊城市黄河河务局，山东聊城 252000）

0 引言

由于小浪底水库拦沙的运用以及调水调沙，黄河下游河道不断下切，同流量下的水位逐年降低，加之引渠淤积、河势变化导致引水口脱离河道等原因，黄河下游灌区也相继出现了引水困难的问题[1]。近年来，位山闸的引水流量也逐年下降，现状引水能力远达不到设计要求，小浪底水库启用前，1983—1999年位山闸年均引黄水量为12.52 亿m3，小浪底水库启用后2000—2016年均引黄水量为9.17 亿m3。根据黄河勘测设计公司的研究成果，现状黄河流量380m3/s 时，位山闸仅可引水30m3/s 左右，为原设计引水能力的12.5%。引水困难问题已影响和制约了灌区的进一步发展。

【研究意义】我国一般采用传统水力学方法预测涵闸引水能力，但这种方法存在部分数据无法获取、数据测量复杂，且需定期分析数据、修订参数、操作不便等问题。为此，寻找既能较为准确预测涵闸引水能力，又具有较高实用性的预测方法对当前黄河下游涵闸改建和灌区运行管理有着重要的意义。【研究进展】人工神经网络具有高度的非线性逼近作用，其中径向基函数神经网络（Radical Basis Function Neural Network，RBFNN）学习效率高、容错性强，近年来被越来越多地应用在非线性拟合领域内，并取得了丰硕的成果。周玲[2]将RBF 网络应用于涵闸流量软测量中，张娜[3]将RBF 网络应用于水位流量关系率定中，都取得了较好的预测精度。但当目标函数十分复杂时，用RBF 神经网络进行训练容易产生局部最优，而遗传算法作为一种模仿生物自然进化过程的算法，可以通过全局并行搜索摆脱局部最优的困扰，搜索到目标函数最优解。王冬雪等[4]建立了一种遗传算法和RBF网络相融合的优化算法，对病虫害所造成的玉米产量损失进行了预测，取得良好预测效果。【切入点】以上研究都是将优化前后的RBF 神经网络应用在涵闸流量测定、水位流量率定等水利或其他领域，对其在涵闸引水能力预测上研究较少，并考虑到涵闸引水能力影响因素广泛，干扰因素众多，具有非线性、变量多的特性，不会出现由于输入向量太少导致的泛化性低的现象，完全适用于此方法。【拟解决的关键问题】为了能有效地对涵闸引水能力进行预测，本文在RBF网络的基础上，用遗传算法对其各网络参数进行优化，并将该模型应用于位山闸引水能力检验和预测上。

1 RBF 神经网络

RBF 神经网络是一种特殊的三层前馈网络,它具有非线性可分的模式空间映射到线性可分状态空间的特性。其主要包括输入层、隐含层和输出层3 部分，输入层和隐含层直接连接，隐含层包含一系列径向基函数，常选用高斯函数，因此隐含层输出为：

式中：φi为隐含层的输出；x为网络输入向量；xc为基函数中心矢量；σ为函数的宽度参数，σ越小，基函数的选择范围就越大。

网络的输出为：

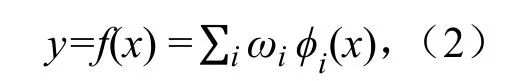
式中：ωi为隐含层到输出层的权值；输出值等于隐含层各神经元的输出与权值的乘积的和。

2 遗传算法GA 优化RBF 神经网络

遗传算法是模仿自然界中生物群体的选择、杂交、变异等行为而发展起来的一种优化算法，是建立在自然选择和自然遗传学机理基础上的迭代自适应概率性搜索算法。利用遗传算法可以在解空间内对解进行多点随机搜索，并找出最优解，由于遗传算法的随机特性，所有解都有被搜索的可能，因而可以找到全局最优解。遗传算法的一般过程可以分为初始化、选择、交叉和变异4 个组成部分[5]。本文利用遗传算法优化RBF 神经网络主要分为以下几方面内容：

1）网络结构的建立。根据样本集暂定神经网络各层节点数，对要训练的输入输出样本归一化处理，然后根据Matlab 工具箱中newrb 函数构建RBF 神经网络，本研究中输入层和输出层的节点数分别为4 和1，初始隐层节点数为11，迭代终止精度为0.001。

2）染色体编码。在试验当中一般采用的是二进制编码，但是二进制编码存在着数据长度大的缺点，在很多实际工程应用当中并不适用。在本文中，采用实数编码，其编码值能够很好地反映现实情况。

3）初始化种群。试验时，设定最大迭代次数为30 次，种群规模为20 个，变量范围为[-1,1]。

4）构造适应度函数。在进行网络训练时，原始数据样本分为训练数据集和测试数据集。通过训练误差和网络规模来确定相应网络的适应度。适应度函数在选取时需要依据具体问题的情况来确定，且该函数须保证为非负。

采用的适应度函数为：

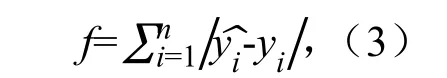
式中：yi为理想的输出值；为实际的输出值。

5）遗传操作。包括选择、交叉和变异操作，选择操作采用轮盘赌法，其基本思想是各个个体被选中的概率与其适应度大小成正比。交叉概率Pc取值通常在0.5～1.0 之间，不宜过小，过小会使搜索停滞。变异概率Pm取值通常在0.01～0.2 之间，不宜过大，过大会使算法变为随机搜索模式。

3 基于GA-RBF 的位山闸引水能力预测模型

3.1 模型建立

开敞式涵闸过流能力计算式[6]一般按堰流公式计算：

式中：Q为过闸流量（m3/s）；σ为淹没系数；ε为堰流侧收缩系数；m为流量系数；n为闸门开数；b为单闸净宽（m）；H0为计入行近流速的闸前水深（m），本次均按闸前水深H计算。

当h/H≥0.9 时，为高淹没出流，其流量计算式为：

式中：μ0为淹没堰流的综合流量系数；h为闸后水深（m）；其他符号意义同前。

涵闸在引水调度运行过程中，可以实时获取闸前、后水位和实测流量等数据，利用式（7）计算可得出理论综合流量系数：

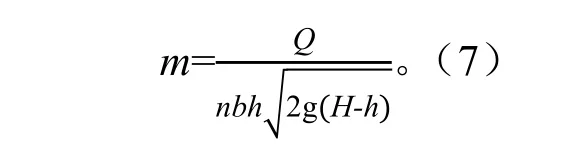
本文由位山闸的闸门开数、闸前、闸后水深和季节因子以及相应的过闸流量建立基于GA-RBF 神经网络的引水能力计算预测模型：输入变量为闸门开数、闸前、闸后水深和季节因子，输出变量为过闸流量。根据选定的样本数据集，利用Matlab[7]进行编程建模。

3.2 模型应用分析

本次研究涉及的水情数据为：闸门开数、闸前、闸后水深、季节因子和对应的实测流量。故分析了位山闸2016—2019年运行期间的实测水情数据，发现西渠每年的实测流量较稳定，故从中挑选出30 组具有代表性的数据组成样本集。其中前21 组作为训练样本，后9 组作为检验样本。为便于计算，将输入数据进行归一化处理：

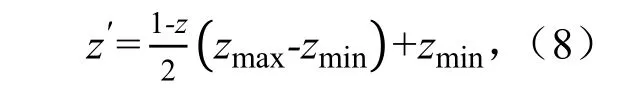
式中：z′为归一化后的数据；z为实测样本数据；zmax、zmin分别为样本数据中的最大值和最小值。对于本次所选的样本中，最大闸前水深为2.17m，最大闸后水深为2.03m，最大闸门开数为5 个，最大实测流量为110.6m3/s。

检验样本预测结果见图1。直接回归拟合方法是结合最小二乘法[8]并运用Matlab 的cftool 工具箱对闸前、闸后水头（H、h）和综合流量系数m进行拟合，建立m与h/H之间的函数关系，再利用式（5）推求出拟合流量。拟合曲线见图2。

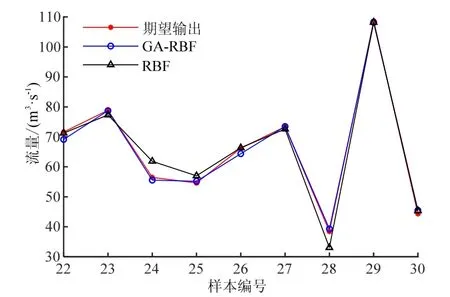
图1 检验样本预测值和真实值Fig.1 Predicted value and true value of test sample

图2 m～h/H 直接回归拟合曲线Fig.2 m～h/H direct regression fitting curve

选取拟合效果最好的幂函数方程：

该方程拟合决定系数[9]R2为0.9041，存在显著相关性，能满足拟合需求。

对以上几种方法和传统水力学方法计算流量与实测流量的相对误差进行计算，结果见表1。由表1可知，传统水力学方法、直接回归拟合方法、RBF神经网络方法和GA-RBF 神经网络方法的相对误差整体呈逐渐降低的趋势，通过式（10）计算，GA-RBF神经网络方法预测结果的平均误差为1.64%，而水力学方法、直接回归拟合方法和RBF 神经网络方法的平均误差分别为27.96%、17.00%和3.82%，GA-RBF模型误差明显低于其他3 种方法，说明该方法的预测精度较高。平均误差按照式（10）计算：

表1 不同模型结果对比Table 1 Comparison of different model results

式中：E为平均误差；qi为实测流量值；为计算流量值；n为验证样本的数量。

图3 为计算流量与实测流量对比。由图3 可知，传统水力学方法拟合效果最差，说明对运作久远涵闸的引水能力进行计算不能完全按照理论方法，需根据实际经验修正率定相关系数；直接回归拟合方法计算结果优于水力学方法计算结果，但该方法泛化性不高，往往只能用做模型对比分析；而神经网络方法的整体趋势最趋近于实测流量，证明该方法拟合效果较好；其中GA-RBF 神经网络拟合效果更优，说明GA-RBF模型的预测精度高具有普适性，可用于对改建工程引水能力进行预测。

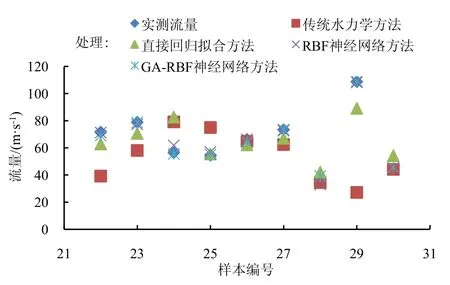
图3 不同方法计算结果与实测流量对比Fig.3 Comparison of calculation results with different methods and measured flow

3.3 基于GA-RBF 神经网络模型的引水能力预测

由上文分析可知，基于位山闸实测水情数据建立的GA-RBF 神经网络模型预测精度高，逼近能力和自适应能力强，拟合效果好。本研究根据位山闸改造可研中提出的改造方案（涵闸底板下降1.09m）和闸后输沙渠下挖方案，利用该模型对改建后位山闸的引水能力进行预测。

在极限冲刷水位38.6m 情况下，拟改建位山闸对应的闸前水深为1.19m，闸门8 孔全开时能保证120m3/s 的引水能力，闸门开4 孔时能保证60 m3/s的引水能力。分析训练样本数据发现闸孔全开时闸前后水头相差很小，故本次用于预测的闸后水深取1.08～1.16m 之间，预测样本见表2。

表2 模型预测样本Table 2 Model prediction sample

结合表2，分别考虑汛期和非汛期的情况，利用已训练好的GA-RBF 模型对改建后位山闸的引水能力进行预测，结果见图4 和图5。

图4 汛期预测结果Fig.4 Forecast results during the flood season

图5 非汛期预测结果Fig.5 Forecast results during non-flood season

由图4 可知，汛期预测值约稳定在70 m3/s，随闸后水深减小变化极小，表明此时涵闸引水能力受闸后水深影响较小，且引水能力远远满足设计要求；非汛期预测值基本介于56～61 m3/s 之间（图5），且随闸后水深降低呈线性递增的趋势，闸后水深每减少0.01 m，引水能力约增加0.6 m3/s，该情况基本能保证其引水能力达到设计要求，证实了闸后输沙渠下挖对引水能力有明显提高。同时要定期对闸门前后进行清淤，防止因闸门淤积影响正常的引水调度。

4 讨论

高淹没出流态下，闸前、闸后水深是影响涵闸引水能力的主要因素。本研究主要提出了3 种方法来计算位山闸引水能力，其中水力学方法计算误差较大的原因可能是人工实测数据的系统误差和现状涵闸边墩淤积严重所致，这与已有研究结果相一致[10]。直接回归拟合方法的拟合结果较好，说明高淹没度下泄流流量系数对淹没度h/H尤为敏感[11-12]。李红利等[13]和刘志平等[14]利用GA 训练优化了RBF 神经网络的中心矢量x，徐杰[15]利用GA 训练优化了RBF 神经网络隐含层到输出层的权值ω，而赵志刚等[16]利用GA 训练优化了RBF 神经网络的中心矢量x和宽度参数σ，与传统的训练算法相比，以上的优化方法经过仿真结果证明了其有效性，本文引入季节因子[2]作为RBF 神经网络的一个输入向量，并扩大优化对象，利用GA 优化RBF 神经网络的中心矢量x、宽度参数σ和隐含层到输出层的权值ω，找到一个较优解，然后将其作为初始参数对RBF 网络进行训练，结果表明优化后的RBF 神经网络预测更高，这与杜辉[17]等基于GA-RBF 组合模型对大坝位移监控的预测结果较为相似。

预测精度得到了提升，但本研究仍存在一些不足，首先本研究选取的训练样本数据较少，可能造成所建模型的泛化能力不强，训练的预测模型可能会有偶然性，论证力度不够，后续还需采集加入更多的实测训练样本。本次预测只考虑了黄河极限冲刷的情况，正常运行期间的引水能力预测由于没有理论数据支撑所以有待进一步探讨。另外此次对RBF 神经网络优化前后的平均误差相差不大，说明利用GA 优化RBF的程度有限，而为了增强GA 的全局寻优能力，必须扩大种群规模n、提高交叉概率Pc和变异概率Pm，以增强群体在GA 演化中的多样性，但是，过大的种群规模与少的计算量要求之间、过高的变异概率与算法收敛性之间存在无法克服的矛盾，因此下一步有必要在全局优化能力及收敛速度二方面对GA进行改造，例如考虑黄永高[18]等对遗传算法的自适应改造，通过自适应改变交叉概率Pc和变异概率Pm，保持多样性，防止早熟收敛，从而提高算法的计算速度和精度。