核电厂安全注入系统可靠性评估研究

王保平 赖建永 尹莎莎 张玉龙 余小权

（中国核动力研究设计院核反应堆系统设计重点实验室，四川 成都610041）

0 概述

随着核能的发展，人们对于核电站的安全控制要求越来越高。在任何情况下，保证堆芯产生的热量能够及时地输出是保证核电安全的关键[1]。当发生失水事故时，安全注入系统能够快速地向反应堆堆芯补水，实现应急堆芯冷却，保证反应堆堆芯不发生裸露。因此，研究安全注入系统的可靠性对保证核反应堆安全问题具有实际意义。

目前的系统可靠性评估方法仅依靠经验反馈法等定性方法[2]，无法判断机械设备和系统的损耗程度，没有对机械设备和系统可靠性进行量化的分析。本文以安全注入系统为研究对象，充分了解安全注入系统的工作原理、功能以及运行流程。根据核电站安全注入系统设备的失效时间数据，利用威布尔分布[3]，建立设备的失效模型，从而获知系统在某个运行时间点的可靠性理论数据，实现对某时间下系统可靠性参考值的预判，给系统安全运行及系统维护提供参考依据。

1 建模方法

设备可靠性分析主要通过对实验数据进行采集、分析并建立可靠性模型。其中一种方法将所获得的实验数据拟合为一种分布形式，如正态分布、泊松分布等，并通过实验数据对其分布参数进行求解，最终获得该部件的可靠性分布模型。本文将对安全注入系统各部件的失效数据进行分析，利用不同的拟合方法求解各部件的威布尔分布参数。

1.1 威布尔分布模型

威布尔分布是一种广泛使用的分布形式，在1951年被瑞典工程师Weibull详细解释。作为一种连续性概率分布，威布尔分布被用于工业制造、天气预测、风速分布、设备可靠性和失效性分析等领域。威布尔分布主要包括两参数分布形式和三参数分布形式，其中，三参数包括位置参数、形状参数和尺度参数。

三参数威布尔分布的概率密度函数为：

故累积失效概率密度函数为：

失效率大小为：

式中，β＞0为形状参数；γ≥0为位置参数；η＞0为尺度参数。

1.2 实验数据处理方法

由于实验中所采集数据为某部件失效或故障时的运行时间，无法得到其具体的可靠度大小，即无法进行模型的直接求解，因此，需要建立运行时间与可靠度之间的关系。其中，对于原始的样本数据，当使用威布尔分布模型时，利用近似中位秩公式对近似可靠度进行求解可获得较好的结果，近似中位秩公式为：

其中，i为当前样本排序，N为样本总数，由此即可计算得到实验失效时间ti所对应的近似可靠度大小R（ti），并利用参数估计方法对参数进行估计计算，得到威布尔分布的参数。

对拟合后的曲线参数，本文采用计算其相对均方根误差（NRMSE）来评价模型精度。具体公式如下：

2 设备可靠性分析

通过对各设备的失效时间进行记录，可以得到设备的失效数据，对失效数据进行处理后，通过上文中的方法对处理后的数据进行威布尔分布参数估计，从而得到模型参数，建立设备的可靠度模型。本文对于已知的止回阀、隔离阀、流量控制阀、低压安注泵、试验管线阀、高压安注泵等设备的失效数据进行处理，得到威布尔分布的参数并进行比较分析。

对我国核电站反应堆机组的安全注入系统中止回阀的原始失效数据进行分析处理。通过双线性回归法[5]、极大似然估计法、支持向量机法[6]以及灰色估计法等方法拟合得到止回阀的形状参数估计值β^、尺度参数η^以及位置参数λ^及相对均方根大小，图1给出了不同方法分别对两组电站数据的拟合曲线。

图1 止回阀原始失效数据拟合曲线

从表1中可以看出，利用双线性回归法计算得到的威布尔分布模型相对均方根误差最小，与实际数据最贴合，但其计算得到的γ值小于0，不符合实际，因此可认为模型建立错误，其余四种方法中，选择第一个失效数据作为γ值后再利用最小二乘法进行计算，模型与实际失效数据间相对均方根误差最大，其余三种方法拟合得到的模型相对均方根误差相近，可看出利用极大似然估计法拟合得到的模型与实际失效数据最接近，故使用极大似然估计法对止回阀进行可靠性建模。

表1 止回阀原始失效数据拟合结果

因此，止回阀所建立的可靠度模型为：

相对均方根误差（NRMSE）为0.135 8。

采用上述方法，依次对安全注射系统隔离阀、流量控制阀、试验管线隔离阀、低压安全注射泵、高压安全注射泵的电厂实际运行参数进行分析迭代，得到各个设备随运行时间的威布尔分布曲线三个参数，如表2所示。

3 系统可靠性分析

安全注入系统根据运行状态可以分为三个阶段，每一个阶段所使用的管线和设备都不相同，且高、低、中压安全注入系统均独立运行，因此，可根据设备间的逻辑关系绘制可靠性框图[7]，计算得到各安注系统的系统可靠度[8,9]。

3.1 直接注入阶段

在直接注入阶段，高压安注系统、低压安注系统、中压安注系统的可靠性框图及可靠度计算如下：

（1）高压安注系统如图2所示。直接注入阶段高压安注系统的可靠度为：

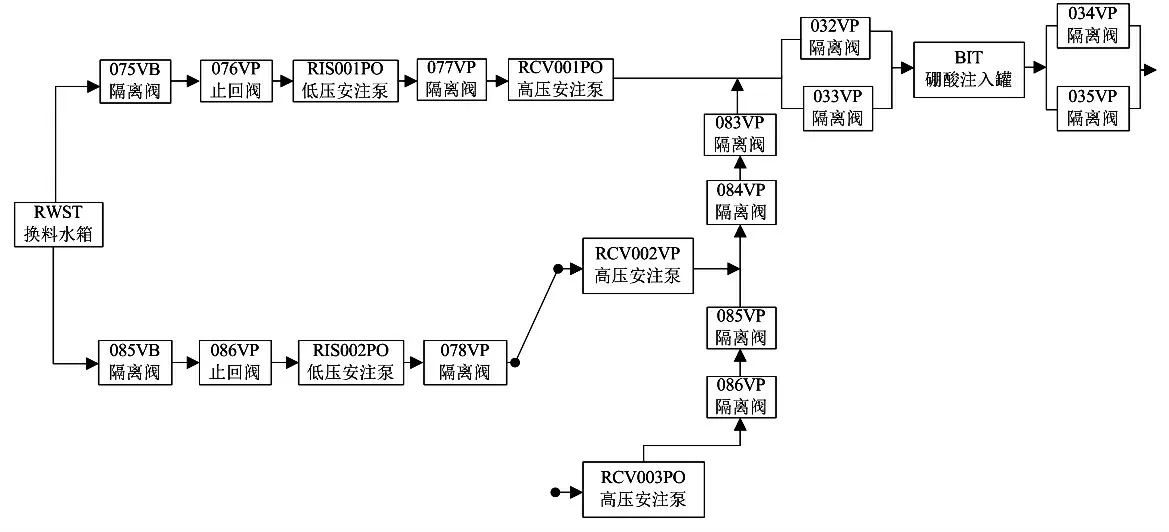
图2 直接注入阶段高压安注系统可靠性框图

式中，RHP为高压安注泵可靠度；

RI为隔离阀可靠度；

RR为止回阀可靠度；

RLP为低压安注泵可靠度。

（2）低压安注系统如图3所示

图3 直接注入阶段低压安注系统可靠性框图

直接注入阶段低压安注系统的可靠度为：

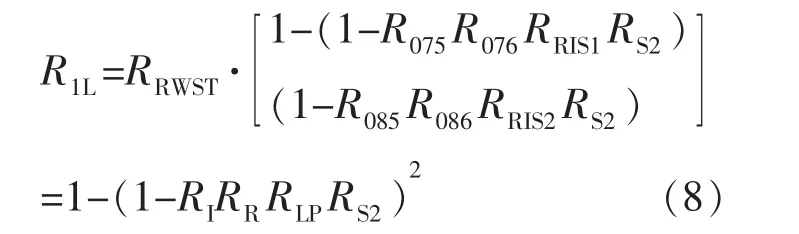
（3）中压安注系统如图4所示。直接注入阶段中压安注系统的可靠度为：

图4 直接注入阶段中压安注系统可靠性框图

3.2 再循环注入阶段

在再循环注入阶段，高压安注系统、低压安注系统的可靠性框图及可靠度计算如下：

（1）高压安注系统如图5所示

图5 再循环注入阶段高压安注系统可靠性框图

根据以上系统可靠性方框图，可求得再循环注入阶段高压安注系统的可靠度为：

（2）低压安注系统如图6所示

图6 再循环注入阶段低压安注系统可靠性框图

根据以上系统可靠性方框图，可求得再循环注入阶段低压安注系统的可靠度为：

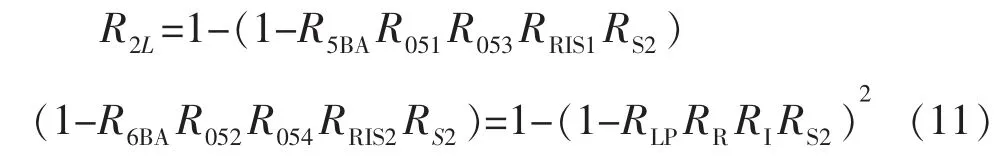
3.3 冷热管同时注入阶段

在冷热管同时注入阶段，高压安注系统、低压安注系统的可靠性框图及可靠度计算如下：

（1）高压安注系统如图7所示。根据以上系统可靠性方框图，可求得冷热管同时注入阶段高压安注系统的可靠度为：

图7 冷热管同时注入阶段高压安注系统可靠性框图

（2）低压安注系统如图8所示。根据以上系统可靠性方框图，可求得冷热管同时注入阶段低压安注系统的可靠度为：

图8 冷热管同时注入阶段低压安注系统可靠性框图

基于上述可靠性框图和可靠度计算模型，本文计算预测了安全注入系统不同任务阶段的可靠性随系统运行时间的变化曲线，如图9所示，从图中可以看出在运行1年后系统可靠度开始下降，在运行1.4年后可靠度下降趋势缓慢，而在系统运行1.8年后系统可靠度急剧下降。

图9 安全注入系统可靠度趋势变化

4 结论

以我国核电站反应堆为研究对象，首先通过对电站安全注入系统实际运行数据收集，采用威布尔分布模型，利用线性回归、最小二乘法、灰色估计法以及极大似然估计法等拟合方法，得到安全注入系统各泵、阀设备的可靠度模型最优参数。进而利用可靠度串并联模型得到电站安全注入系统不同运行阶段的可靠性模型，并通过计算预估安全注入系统不同任务阶段的可靠性随系统运行时间的变化情况，从而为电站安全注入系统的通用质量特性评估提供依据。