城市道路PPP项目利益相关者博弈研究
2021-06-29汪卓典李重阳
汪卓典,方 俊,李重阳
(武汉理工大学土木工程与建筑学院,武汉 430070)
为满足城市人口日益增长和发展需要,通达城市各地区的城市道路的建设被提上日程。基础设施建设所需的巨额资金导致政府承担巨大金融风险,为此国家发布《关于推广运用政府和社会资本合作模式有关问题的通知》(财金[2014]76号文)以促进政府和社会资本合作。由于PPP(Public-Private Partnership)模式涉及多个利益相关者,笔者构建博弈模型进行分析,演化预期以为城市道路PPP项目发展提供建议。
1 城市道路PPP项目利益相关者识别
利益相关者分析(stakeholder analysis)作为世界银行、亚洲发展银行等组织明确规定在其贷款项目决策阶段必须使用的分析工具[1],被国内外学者广泛应用于大型建设项目的管理和投资当中[2]。而对于利益相关者的定义,学术界并不统一,1984年Freeman对广义利益相关者的定义为“任何可以影响企业目标或者被目标影响的团体或个体”[3]。
根据利益相关者五个维度特征准确识别出城市道路PPP项目的利益相关者从而确定博弈的主体,是构建博弈模型的前提。王进和许玉洁通过大量调查问卷采用SPSS(Statistical Product and Servise Solutions)分析后识别出政府、建设单位、环保部门、投资人等12个大型工程项目关键利益相关者[4],李静菲结合理论与实践将PPP项目划分为边缘、核心和一般三类,政府和社会资本是核心利益相关者[5]。
2 城市道路PPP项目核心利益相关者的博弈分析
对政府和社会资本这两个核心利益相关者进行博弈分析,由于城市道路工程的公益性质,从财政部PPP中心的数据来看,回报机制大部分采用的都是政府付费的形式,即政府每年向社会资本支付可用性付费作为投资回报,使得社会资本回收成本并取得合理利润。但政府为保证工程建设和运营质量,设立绩效考核机制进行监督,并将可用性付费的一部分纳入考核范围。因为双方的有限理性和有限信息性,政府不得不采取监督措施来检测社会资本是否采取了机会主义,从而对绩效考核部分付费做出决策。
2.1 博弈假设与支付矩阵
假设政府和社会资本的博弈是在有限理性条件下进行的,双方具有不完全信息性,预先并不知道对方采取的策略,只能通过自己已有的信息和对方的实时策略来决定自己下一步策略。社会资本可采取的策略主要有积极努力态度和机会主义两种,而政府方采取的策略主要有严格监督和不作为两种。政府有两种策略,A1为严格监督策略,A2为放任不管策略;社会资本的积极努力态度为策略B1,机会主义为策略B2。政府采取严格监督策略时,发现社会资本以积极努力态度完成工程则给予全部可用性付费,若发现社会资本存在机会主义行为,则不给予绩效考核部分付费。当政府采取放任不管策略时,不管社会资本采取什么策略均给付全部的可用性付费。
假设政府以x的比例采取严格监督策略,社会资本以y的比例采取积极努力态度。则政府采取放任不管策略的比例为(1-x),社会资本采取机会主义策略的比例为(1-y)。政府的可用性付费中,固定部分为a,绩效考核部分为b,政府采取严格监督策略而产生的成本为c,社会资本积极努力态度的额外成本为d,社会资本采取机会主义策略时获得额外收益m,同时给政府带来m的利益损失。工程完成时政府的基本收益为s1,社会资本获得的基本收益为s2。由此可构建政府和社会资本的支付矩阵(表1)。

表1 支付矩阵
2.2 构建博弈模型
政府采取严格监督策略的期望收益
E(A1)=y(s1-a-b-c)+(1-y)(s1-m-a-c)
(1)
政府采取放任不管策略的期望收益
E(A2)=y(s1-a-b)+(1-y)(s1-m-a-b)
(2)
政府采取混合策略的期望收益
E(A)=xE(A1)+(1-x)E(A2)
(3)
社会资本采取积极努力态度的期望收益
E(B1)=x(s2-d)+(1-x)(s2-d)
(4)
社会资本采取机会主义策略的期望收益
E(B2)=x(s2+m-b)+(1-x)(s2+m)
(5)
社会资本采取混合策略的期望收益
E(B)=yE(B1)+(1-y)E(B2)
(6)
根据式(1)~式(3)可得到政府严格监督策略时的复制动态方程和微分方程
(7)
F′(x)=(1-2x)[b(1-y)-c]
(8)



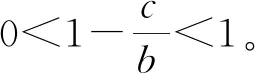
因此政府的策略选择与绩效考核部分可用性付费b和严格监督产生的成本c有关。
根据式(4)~式(6)可得到社会资本积极努力态度的复制动态方程和微分方程分别为
(9)
F′(y)=(1-2y)(bx-m-d)
(10)





(11)
行列式值大于零且迹小于零的均衡点称为ESS点;行列式值大于零且迹大于零的点称为不稳定点。若点(x1,y1)存在,由于其迹等于0,所以是中心点。各均衡点行列式值和迹值见表2。

表2 各均衡点行列式值和迹值
3 博弈分析
根据不同情况可以得出4种相位图(图1),根据相位图分析演化路径可得:

1)当b>c,且b>m+d时,会开始无限循环没有稳定状态。
2)当c 3)当m+d 4)当b 由博弈分析可知,城市道路工程PPP项目中,政府希望单纯通过监督以决定是否给予绩效考核部分可用性付费的方式无法达到社会资本采取积极努力态度的均衡状态。为达到预期效果,可采取以下措施: a.政府要在不减少绩效考核部分可用性付费比例的同时尽量减少严格监督策略产生的成本,这就要求监督形式的多种多样,如将周边居民和沿线社区的满意程度也纳入考核范围,在增加约束力的同时还可以减少监督考核成本。 b.政府绩效考核只决定部分可用性付费的给予,仅允许社会资本获取合理利润,无法对社会资本起到激励作用。因而政府可采取将城市道路工程和其他市政项目如地下管廊等进行打包的形式,使项目有自身营利能力促进社会资本的积极性。也可将沿线道路的加油站开发权、广告位出让权等作为对社会资本积极努力态度的激励机制,来最大程度避免社会资本采取机会主义策略。4 结论及建议
