基于随机森林的大坝渗流监测研究
2021-06-29辛晟铭
辛晟铭
(新疆头屯河流域管理局 水利管理中心,新疆 昌吉 831100)
0 引 言
大坝的渗流情况监测[1-2]一直以来都是大坝安全监测的重点项目,由于水库大坝在运行中受到很多因素的影响,通过观测渗流情况最能直观地反映它的稳定状况。如果能够根据监测数据创建精度准确的预测模型,对一定时期内的渗流进行准确预测,便能跟踪大坝的安全变化状态,必要时采取适当措施杜绝安全隐患。因此,众多学者一直致力于研究精度更高的大坝渗流监测模型。这种由实际数据形成预测模型的过程,传统上都是通过数学模型来构建的。在实际应用中,主要有统计模型[2-3]、确定性模型[4-5]和混合型模型[5-6]3种数学模型,通过统计学的原理展现监测值和影响量之间的相互关系。然而,由于渗流的成因较复杂,这些传统的建模方法受变量多重共线性的影响或模型参数的选取不恰当,导致精确度往往不高。
随着机器学习算法的发展,学者们利用诸如人工神经网络[7-8]、遗传算法[9]、蚁群算法[10-11]、支持向量机[12-13]等算法来创建大坝监控模型,取得了一定成果。但这些模型尚未成熟,计算量较大,且不稳定,无法彻底解决多变量共线性的影响。
随机森林算法也是机器学习的一种,它能够解决多变量之间的交互作用和非线性关系,在无大幅增加计算量的情况下提高了分类、回归问题的准确率。通过随机森林创建的模型能够有效地分析非线性及共线性存在某种关联的数据[14],且无须事先假定数据的分布,这些特点使得其在生物学[15-16]、土壤学[17-18]、医学[19]等专业方向得到较大程度的应用,但在水库大坝渗流监测方面应用较少。此外,随机森林算法能够有效处理噪音和异常数据,不易出现其他机器学习算法的过拟合问题。为此,本文基于随机森林算法构建大坝渗流监测模型,对以往的监测资料进行训练、学习及分析,并与BP神经网络进行对比,验证该模型的可行性和有效性。
1 随机森林回归算法模型
决策树又称为分类回归树,是随机森林的基础组成部分。决策树是一种预测模型,它所表现的是统计对象的值与属性之间的映射关联。决策树中的节点表示某个对象,每个分叉就表达该对象的某种属性,叶节点则表示对象的值。决策树只有单一的输出,类别较多时,准确度会下降。而随机森林可以将许多决策树通过Bagging方法结合[20]起来,以提升分类回归的正确率。
随机森林的本质是一种集成学习的方法,从分类功能来看,多棵树会有多个分类结果。而随机森林集成了所有的分类投票结果,将得票最多的分类结果作为模型的输出。随机森林还可以用于回归,用于回归分析的随机森林可通过训练得到随机向量参数,采用简单平均法,对多个分类回归树得到的回归结果进行算术平均得到最终的模型输出。
回归算法实现:随机森林回归(Random Forest for Regression,RFR)模型是由多颗回归树组成。在实际运用中,每棵决策树的特征选择不一样,所以它们拥有各自对应的随机向量,那么T棵树就是一组随机向量序列fi(i的值为大于0的整数)。同分类模型不同的是,回归模型的因变量是连续的数值。假设训练集是从随机向量X、Y中独立抽取出来,那么任意数值的预测值H(X)是对T棵回归树{h(f,XT)}的取算数平均数得到的。
随机森林回归算法的构建流程如下:
步骤1:利用bagging思想,从训练集中进行有放回的抽样,产生训练子集。
步骤3:重复以上步骤,构建N棵回归决策子树,形成不剪枝的森林{h(f,XT)}。
步骤4:将森林中每棵树的预测值进行算术平均,输出最终结果。
步骤5:模型的效果采用袋外数据来评价(袋外数据可以用来估计回归树的泛化误差,而不用交叉验证)。
回归分析会出现多重共线性的现象,影响回归模型的准确性。多重共线性是指回归模型中的解释变量之间由于存在一定程度的相关关系,如果存在比较严重的共线性问题时要用特定算法或者降维处理。如果模型仅用于预测,则只要拟合程度好,可不处理多重共线性问题。随机森林因其不用选择变量,而且拟合程度良好,所以由其创建的回归模型不受多重共线性的影响。
2 基于随机森林算法的大坝渗流预测模型构建
2.1 模型输入变量
大坝渗流的影响因子较多且复杂,由于渗流测压管水位变化趋势基本符合土坝渗流特性[21],所以根据渗流测压管的水位来反映渗流量。此次研究对象为土石坝,水库中的水从上游向下游渗透时,因为土壤阻力的作用,需要一定时间才能流到测压管内,该时间同上游水位相关联,所以将一定时间段的上游水位判定为影响因子。降雨时会产生地表径流,该径流通过坝体入渗,所以降雨量也是影响因子。随着大坝的正常运行时间累积,土石坝逐渐坚固稳定,土壤入渗的可能也就越来越小,同时水流夹杂的泥沙导致淤泥积累也在一定程度上影响了渗流的状态,这些因素都会造成到测压管的水位变化。综上,测压管水位的重要影响因子分别包括一定时间段的上游水位、一定时间段的降雨、下游水位和时效因子[22]。用公式表达如下:
h=hu+hd+hp+hσ
(1)
式中:h为测压管的水位,它由4个分量组成;hu为上游水位;hp为降雨量;hd为下游水位;hσ为失效因子。
2.1.1 上游水位值
水流经过上游坝面、经过土壤渗透到达测压管需要一段时间,测压管的水位是滞后于水库水位的,所以用这段时间的平均水位来表达。
(2)

2.1.2 下游水位值
下游水位的变动是不大的,所以直接用水位值的回归形式来表达,即:
hd=αdhd
(3)
式中:αd为回归系数;hd为下游水位值。
2.1.3 降雨量

(4)

2.1.4 时效因子
大坝在运行一段时间后,内部的土壤逐渐趋于稳定和固化,它的渗透性能也会发生改变,水库上游坝面的表面也因时间推移形成越来越厚的淤泥,影响到入渗情况。这些情况都受到时间迁移的影响,所以引入时效因子,其表达式如下:
hθ=C1θ+C2lnθ
(5)
其中:C1、C2为回归系数;θ为蓄水初期开始的天数除以100。
2.2 建模工具
为了建立随机森林回归模型,使用R语言的Random forest包来进行。R作为一种统计分析软件,它可以运行于Unix和Windows的操作系统上,因其开源和免费,目前在统计领域得到广泛的应用。在运用R语言创建预测模型时,主要运用predict和mean这两个函数来实现随机森林的回归。
2.3 模型参数
在使用Random forest建立随机森林时,回归决策树的数量ntree和每个节点的特征数量mtry这两个参数是最重要的。mtry由总输入变量开平方求得,它能够决定树与树之间的相关性和算法的强度。在本案例里,输入变量的个数为4,所以mtry取值为2。为了提高模型的运行效率和降低复杂程度,需要等到袋外数据错误率趋于稳定时才能确定ntree的值。一般地,用MMSEOOB(袋外误差平方和)来体现袋外误差的错误率。通常情况下,需要利用它和ntree的关联图来确定ntree。
2.4 建模流程
基于随机森林回归算法的土石坝渗流预测模型的创立步骤如下,建模流程见图1。
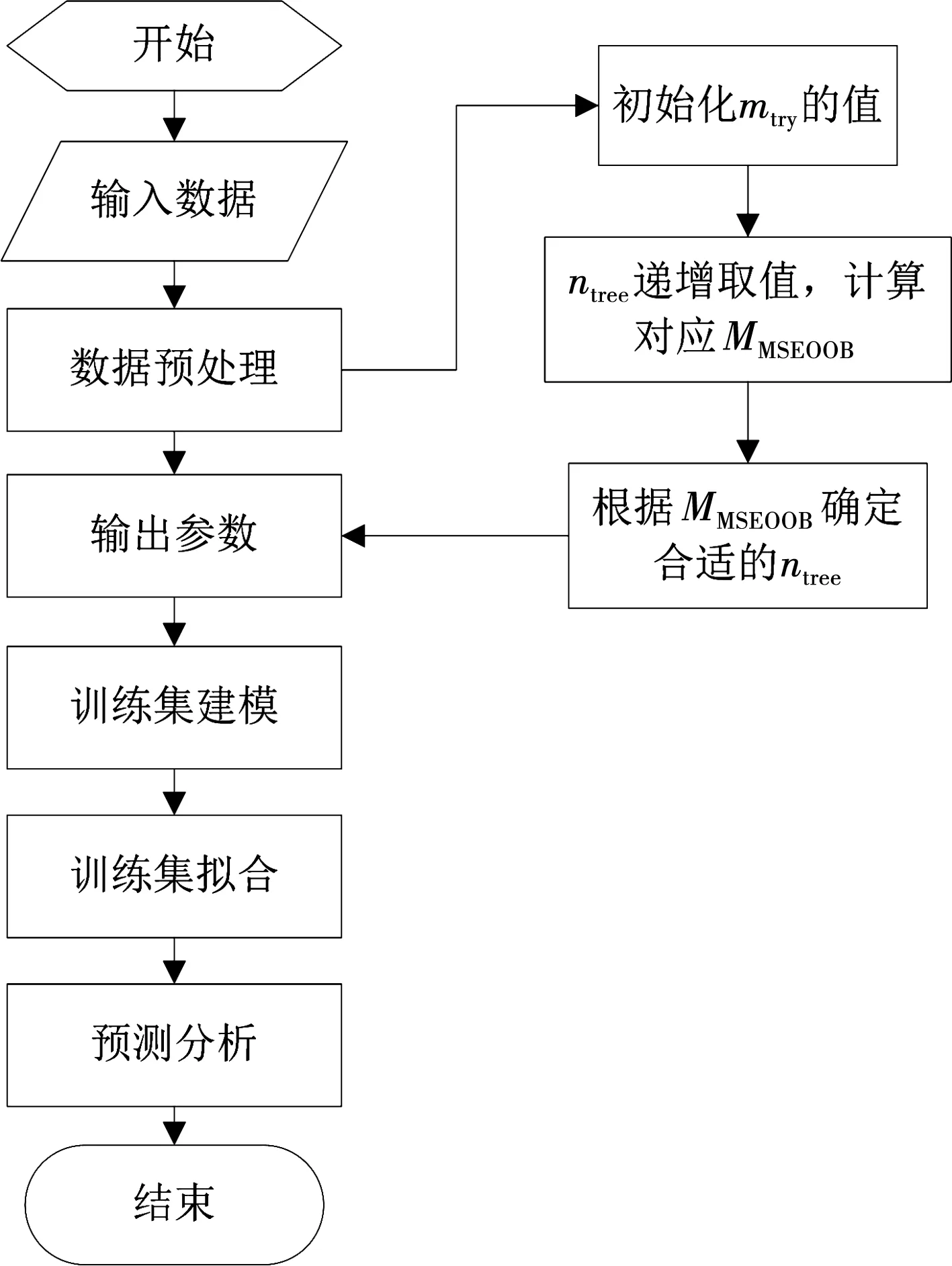
图1 渗流预测模型流程图Fig.1 Dam seepage prediction model flow chart
步骤1 在R语言环境下,调出Random forest程序包,读取渗流监测数据。
步骤2 将特征数量mtry的值设定为2。从100棵回归决策树逐渐递增,观察每次建模得到的MMSEOOB值,当袋外误差率趋于稳定时,选定ntree值。
步骤3 使用mtry和ntree两个参数建模,对原始监测数据进行训练,并对测试集进行预测。
3 案例分析
本文主要选取新疆某水库大坝渗流监测资料,该水库大坝为碾压式黏土心墙砂壳坝。陡山水库坐落在沭河一级支流浔河中下游,控制流域面积431 km2,对其渗流情况的监测尤为重要。
该水库大坝的渗流监测设有3个断面,有24个测压管,选取管口位于坝顶的AP204坝基测压管,资料记录时间为2015年1月至2017年12月。测压管水位的观测周期为:汛期7天一次,非汛期10天一次。将2016年3月至2017年8月这18个月的65组数据作为训练样本,通过组合学习,对2017年9月的6组数据进行预测。
3.1 重要参数的选定
在实际建模过程中,通过观察ntree与MMSEOOB的关联变化情况来确定森林的棵数,当MMSEOOB趋于稳定时,选定合适的棵数。图 2是ntree与MMSEOOB的关联变化图。从图2中可以看到,当森林的棵数达到500时,趋于稳定;达到1 000时,袋外数据误差最小。为了保证模型的准确度,选择1 000作为随机森林回归算法模型的棵数。
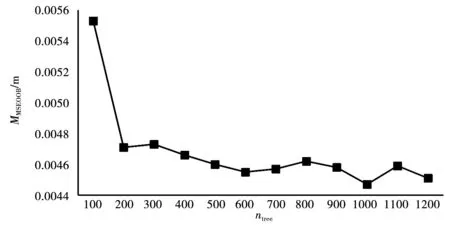
图2 ntree与MMSEOOB关联变化图Fig.2 Association change diagram of ntree and MMSEOOB
3.2 模型应用及结果分析
为了便于对比研究,通过建立随机森林回归模型及BP神经网络模型[23]对测压管的水位进行拟合与预测,其中随机森林回归模型是利用Random forest函数对训练期建模,predict函数对预测期的数据进行拟合。图3和图4分别为AP204测压点在两种模型下的拟合及预测结果。
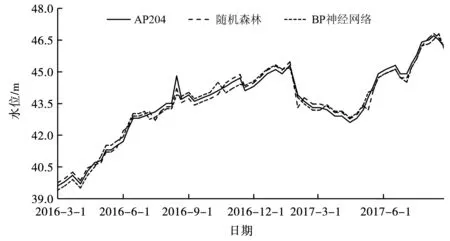
图3 随机森林及BP神经网络回归模型拟合曲线Fig.3 Fitting curves of random forest and BP neural network model
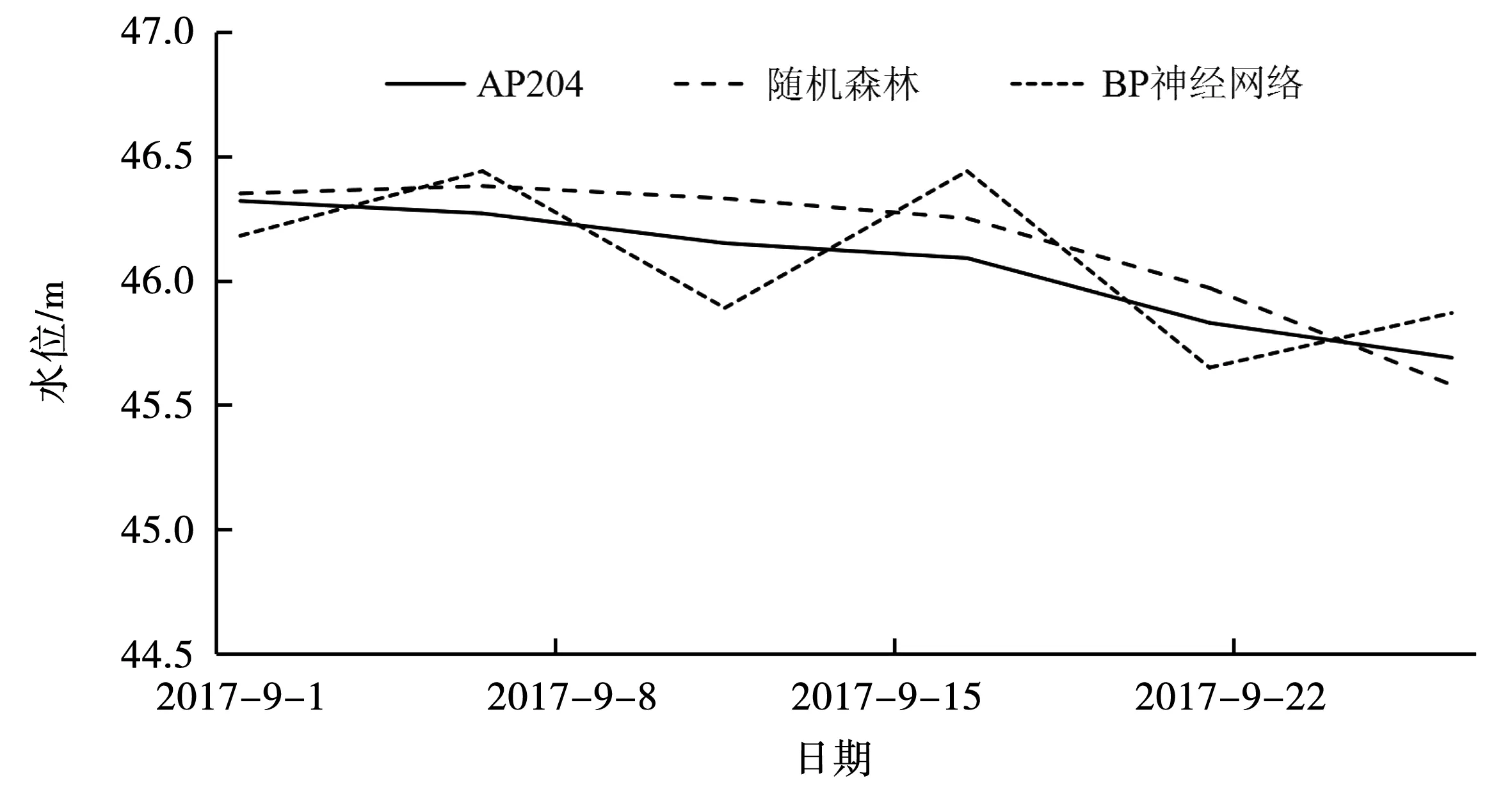
图4 随机森林及BP神经网络模型的预测曲线Fig.4 Prediction curve of random forest and BP neural network model
由图3可以看出,两种模型与实测值的拟合趋势是一致的,样本训练水位处于39~47 m之间,8月份汛期出现峰值拐点,两种模型都能够体现该拐点趋势,但随机森林较为准确。由图4可以看出,预测期测压管实测水位在45.5~46.5 m之间波动,随机森林模型处于相对平滑稳定的状态,而BP神经网络存在波动性。从而可以看出,该土石坝渗流预测模型能够有效地拟合和预测水位值。
本文研究的预测期时间轴较短,在此期间水位的变化也较小,更适合用随机森林算法来建模。BP神经网络需要初始化权值,且需要经过数次测算,才能达到良好的预测效果,消耗过多的计算时间,同时占用大量的内存。随机森林模型可以直接使用样本数据,无需前期处理,且测算数据的过程简便快捷。
一般地,评价一个统计模型的优劣程度,需要判定其精确度和稳定性。本文的模型精度指标选用实测值与预测值之间的平均相对误差、均方根误差这两个指标,稳定性则使用确定性系数R2与计算时间两个指标,通过这4个指标来评价随机森林回归模型和BP神经网络模型的优劣程度。数据对比见表1。

表1 随机森林和BP神经网络模型对比Tab.1 Comparison of random forest and BP neural network model
从表1可看出,随机森林回归模型的确定性系数为0.96,大于BP神经网络,表面其因变量可靠程度高,加之其运算时间比BP神经网络少,所以其稳定性较高。另外,随机森林回归模型的相对误差值和均方根误差值两项指标都小于BP神经网络。综上所述,充分证明其在预测精度和模型稳定方面的优越性。
4 结 论
本文充分利用随机森林回归模型具有的特性,对目前国内水库应用较多的土石坝类建立了渗流监测模型。通过陡山水库多年的监测资料建立训练样本,模型输出的拟合结果和预测结果同实际监测资料的变化趋势相一致。通过对比随机森林回归模型、BP神经网络模型的预测精度与稳定性,确定了随机森林模型的整体优势性,该模型的建立为大坝渗流的精准预测提供了一种新途径。
