基于Maple软件对推广KP方程的对称研究

王芬

(河南科技职业大学,河南周口 466000)

1 李群理论

一般的非线性演化方程可表示为:

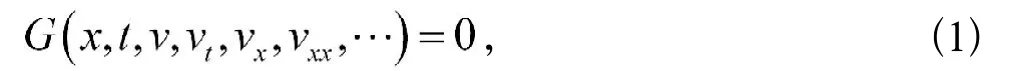
其中G是其变量的已知光滑函数,v=v（x,t）是待求函数。称函数(记σ（v）或σ)为方程(1)的一个对称(symmetry),如果

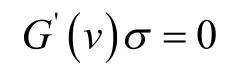
对任意的v都成立,其中G（v）是v及其导数的已知函数,且

19世纪,S.Lie在研究微分方程的基础上,提出了李群理论的思想。由于李群理论相对比较抽象,因此在20世纪70年代以前,这一理论并没有被广泛应用。直到Bluman写了易懂的著作,李群理论才被逐渐广泛地用于研究和求解非线性偏微分方程(非线性发展方程或演化方程)。李群方法是研究微分方程的有效方法之一,应用李群可得到方程的不变解或简化方程。偏微分方程(组)的对称约化的经典方法就是李群方法[1],李群理论有着非常丰富的内容,其中李代数的研究是数学理论中的重要内容。从集合的观点来看,v1和v2可以作为一个线性空间 Ω=span{v1,v2}的两个基来对待。如果规定σ（x,t,v,v x,vxx,L）换位子运算:,则该线性空间还构成代数(满足分配律及数乘交换律的线性空间),称为李代数。假设（x,t）∈R2是自变量。

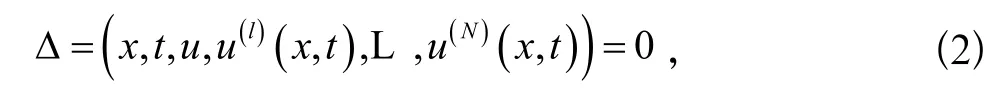
应用经典李群方法,我们考虑无穷小单参数李群变换（x,t,u）,给定:

其中ε是群参数,这就要求方程组(2)在变换(3)下是不变的,同时生成一个关于无穷小元ξ（x,t,u）、τ（x,t,u）和φ（x,t,u）的超定线性方程组,无穷小对称的相关李代数有下面向量场形式:

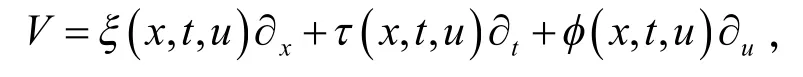
这里 ∂/∂x≡∂x。这个方法完全依靠算法解决问题的,经常涉及复杂代数和辅助运算,这就需要利用Maple软件等符号计算。Maple软件是由加拿大Waterloo大学开发的数学和工程计算软件,不但具有精确的数值处理功能,而且具有无与伦比的符号计算功能,是一种交互式计算机代数系统[2],因而被广泛运用于数学的各个分支领域[3]。

2 优化系统

总的来说,对于全对称群G的每一个s参数子群H,一个微分方程有p＞s个自变量,它会有相应的群不变解,由于总有一定有限数量的子群,因此列出方程所有可能的群不变解是不可行的。我们需要一个有效的、系统的分类这些解的方法——“优化系统”,该优化系统涉及到群不变解的任何一个解。由于元素g∈G且g不属于子群H,该元素使得H不变解转换为其他群不变解[4]。

3 (3+1)维推广KP方程的对称及优化系统

(3+1)维推广KP方程:

对于(3+1)维推广KP方程,采用经典李群方法,要求方程(4)的解集合S:={u:Δ=0}在(3)变换下是不变的。这可以得到有关ξ、δ、κ、τ和φ的线性齐次偏微分超定方程:

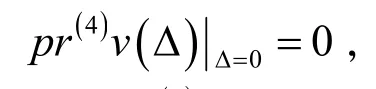
其中pr（4）（v）是向量场的四阶延拓给定为

这里φx,φxx,φtt和φxxxx在文献中被给定。

利用Maple软件得到方程(4)的有关无穷小元的139个方程,其编程源代码如下:

并运用符号计算得到

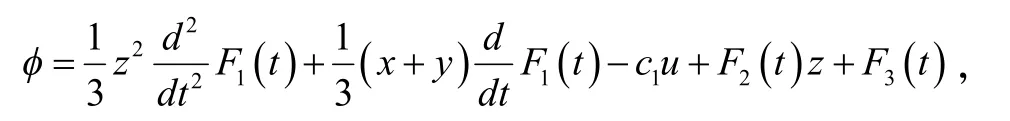
进而得到方程(4)的对称为

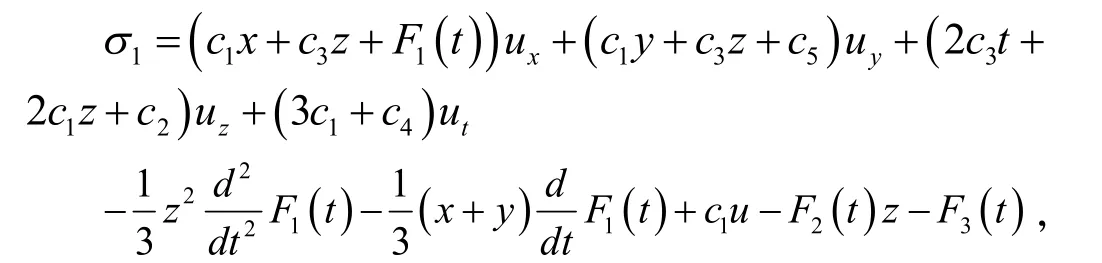
这里是任意常数,F1（t）、F2（t）和F3（t）均为任意函数。

在σ1中,取F1（t）=c6+G1（t）,则可得到(3+1)维推广KP 方程的有限维李代数由下面六个向量场生成,具有如下形式:

即可得到(3+1)维推广KP方程的相关向量场

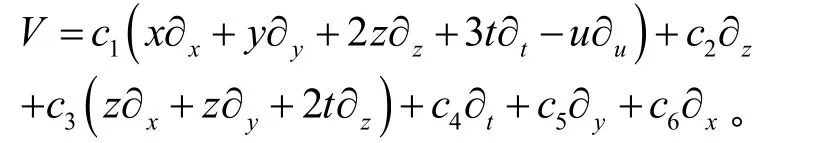
总的来说,一个对称群的子群都有(3+1)维推广KP方程的群不变解,由于列出所有可能的群不变解较复杂,这里引入群不变解优化系统[5]。

解在单参数群下仍是不变解,为了得到这些解,找到产生所有群不变解的最小子群集——优化系统。众所周知,找子群优化系统,等同于找子代数优化系统。本文将子代数问题转化为伴随表示分类问题。

表1 李括号Tab.1 Li brackets

表2 伴随表示Tab.2 Adjoint Representation

4 结论

符号计算是以符号、公式为对象的研究数学问题的算法求解学科,由计算机代替人工推导,实现公式的机器推演,从而大大提高了演算速度,使得复杂的计算变得简单快捷,而这些符号计算需要在Maple平台上实现。本文采用经典李群方法并且运用Maple软件,通过符号计算得到(3+1)维推广KP方程的对称,进而得到该方程的无穷小生成元李代数系统的优化子系统。通过文章的完成,不但给相关的科研人员提供理论依据,而且能够拓宽研究方法的应用范围,使其理论更加完善。