基于短文本相似度计算的工序卡片相似度计算方法

童 伟 王淑营

(西南交通大学 信息科学与技术学院,四川 成都610000)

随着工艺技术的发展，各制造型企业的产品数量和种类不断增多，伴随着产品的工艺设计产生的工序卡片数量也在激增。在如此庞大的工序卡片数量之下，想要靠人工来找出与一张工序卡片相似的其它工序卡片进行推荐几乎是不可能完成的任务，但工艺员在进行工序设计时，与该工艺相似的工序卡片能够为工艺员提供参考，能够极大的提高工艺员的工序设计效率。如何从海量的工序卡片中找到相似的工序卡片是迫切需要解决的问题，而文本相似度判断技术的发展为解决该问题提供了有力的技术支持。本文以机械制造型企业的工序卡片为研究对象，基于工艺的特点，通过结合Jaccard相似度计算方法与Levenshtein距离计算方法，计算出两张工序卡片中各个需要参与相似度判断的项之间的相似度，然后将各项之间的相似度相结合，最终获得两张工序卡片的相似度。

1 相关研究工作

相似度计算算法的选择是本研究最重要的部分，目前，常见的文本相似度计算方法有闵可夫斯基距离、曼哈顿距离、欧氏距离、余弦相似度、杰卡德相似系数、计算编辑距离等，随着信息技术的发展，国内外学者对文本相似度计算方法的研究不断深入，藏润强，孙红光等人基于Levenshtein和TFRSF提出了一种文本相似度计算方法，石彩霞等人提出了一种多重检验加权融合的短文本相似度计算方法，艾楚涵，姜迪等人基于主题模型和文本相似度计算进行了专利推荐的研究，郭浩、许伟等人基于CNN和BiLSTM提出了一种短文本相似度的计算方法，Jiaqi Yang,Yongjun Li等人基于语义和句法信息提出了一种文本相似度的度量方法,考虑到两工序卡片各个项之间文字数量较少,属于短文本的特点，初步选出杰卡德相似系数与计算编辑距离这两种适合计算短文本相似度的方法。

2 方法

2.1 杰卡德相似系数

本文所使用的杰卡德相似系数基本公式为：

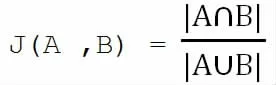
2.2 计算编辑距离

本文所使用的Levenshtein最小编辑距离的计算公式为：

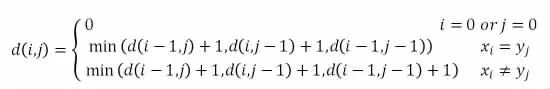
该距离是描述由一个字串转化成另一个字串最少的操作次数，在其中的操作包括插入、删除、替换。可以看出，在同等字符串长度下，两字符串的相似度越高，计算编辑距离的值反而越小，不便于后续计算。因此，本文提出另一种表示计算编辑距离的相似度的方法，将计算编辑距离得出的结果转换为计算编辑距离相似度表示，其公式为：

k=(p-q)/p

p:两字符串中长字符串的长度。

q:最少操作次数。

k:计算编辑距离相似度。

可以看出，在两字符串完全不同时，其计算编辑距离相似度为0，随着字符串相似度的增大，其计算编辑距离相似度也随之增加，在两字符串完全相同时，其计算编辑距离相似度为1。

2.3 分别计算两类工序项间相似度并结合

工序卡片的产品名称、零件名称和工序名称这类项能直接通过单项相似度来判断工序卡片相似度，且工序卡片相似度随这些项相似度提高而提高，将这类项归为一类（下文简称第一类），这类项的相似度计算方法采用结合杰卡德相似系数与Levenshtein最小编辑距离两种短文本相似度计算公式的方法，具体相似度计算公式如下：

第一类工序项单项相似度计算公式

第一类工序项总相似度计算公式

将加工设备名称、夹具名称这类名称相同工序不一定相似，但名称不同工序间差异较大，所以不便于通过单项相似度来直接判断工序卡片相似度的项归为另一类（下文简称第二类）。这些项与工艺相似度虽有较大联系，但与第一类中的项不同，存在一定的特殊性，其特殊性在于：这些项若有一个字不同，则表达了两种完全不同的含义，如工艺车床与工艺铣床只有一字之差，表达的却是两种完全不同的设备，其能处理的工艺也完全不同。所以这些项不便于用文本相似度判断方法判断相似度。本文根据这一特殊性，通过实验后，提出一种较为实用的判断此类项相似度的方法：若两张工序卡片中的此类项的同一项完全相同，则此项相似度为1，若不同，不管差异大小，此项相似度记为0，相似度计算公式如下：

第二类工序项单项相似度计算公式

第二类工序项总相似度计算公式

在得出两类工序项的相似度后，需对其进行结合。两类项的相似度都对两张工序卡片的最终相似度有极大影响，需避免出现若某类项相似度极高，即使另一类相似度不高，得出的工序卡片最终相似度也较高的情况，所以采用将两类项的相似度相乘，得出最终相似度的方案。计算公式如下：

总相似度计算公式

3 实验及结果分析

本次实验使用python语言编写了pdf文字提取代码，提取出收集的2000余张汽车制造领域工序卡片中的文字信息，转化为结构化数据后存储到数据库中，为后续的实验做准备。

咨询相关工艺员后对这2000余张工序卡片进行分类，将相似工序卡片归为一类，编写python程序根据上述方法分别判断各工序卡片与其余工序卡片的相似度，将得到的结果与之前的预分类结果进行比较，测试在对不同项赋予不同权重时所得结果的准确度，以此得到各项的最佳权重。

3.1 计算第一类工序项相似度

此类项包括产品名称、零件名称和工序名称，这些项的相似度能直接代表两工序的相似度，其中工序名称与工序的联系最为紧密，是判断工序相似度最为重要的依据[5]，因此该项的相似度在第一类工序项相似度中占有最大比重（图1、2）。

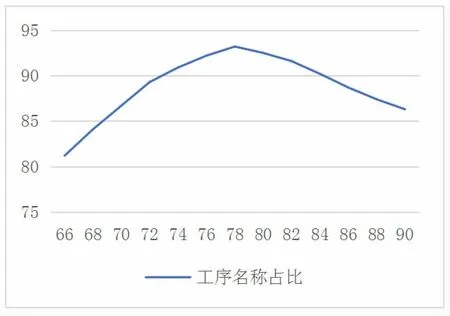
图1 不同工序名称占比下最高相似度计算准确度

图2 78%工序名称占比下不同零件名称占比相似度计算准确度

图3

通过实验得出，在判断第一类工序项相似度时，各项相似度所占比重为：产品名称7%、零件名称15%、工序名称78%时，得出的结果较优。在计算相似度时，使用杰卡德相似系数与计算编辑距离相似度相结合的方法，两种相似度计算方法得出的相似度值各占第一类工序项相似度最终结果的50%。例如有如下两张工序卡片片段。

这两张工序卡片的产品名称与零件名称的杰卡德相似系数与计算编辑距离均为1，工序名称的杰卡德相似系数为2/6=0.33 ，工序名称的计算编辑距离相似度为(5-3)/5=0.4 工序名称最终相似度为(0.33 +0.4 )/2=0.37 ，其第一类工序项相似度为1*0.07 +1*0.15 +0.37 *0.78 =0.5086 。

3.2 计算第二类工序项相似度

此类中的项包括设备名称和夹具名称，通过大量实验计算在第一类项取最优的情况下，这两项在占不同比重下相似度计算的准确度，实验情况如图4所示。

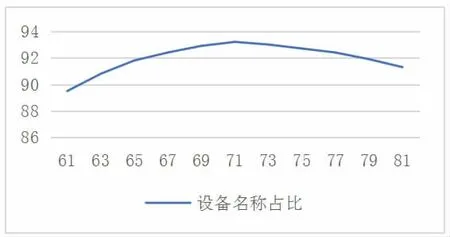
图4 第一类工序项最优占比下不同设备名称占比相似度计算准确度

实验得出，在判断第二类工序项相似度时，各项相似度所占比重为：设备名称71%、夹具名称29%时，得出的结果较优。例如有如下两张工序卡片片段（图5）。

图5

这两张工序卡片的设备名称相似度为1，夹具名称相似度为0，其第二类工序项相似度为1*0.71 +0*0.29 =0.71 。

3.3 结合两类工序项相似度

分别得到两类项的相似度值后，再将这两个相似度值相乘，最终得到这两张工序卡片的相似度值。例如结合3.1 、3.2 得出的两类工序项的结果，工序卡片一、工序卡片二最终相似度为0.5086 *0.71 =0.361 。

结束语

本文针对工序卡片信息，从工序卡片的各工序项入手，将工序项分为两类，利用文本相似度计算方法计算第一类工序项相似度，针对第二类工序项的特殊性，将第二类工序项按是否相同设置固定的相似度，再根据工序的特点进行结合，最终得出两张工序卡片的相似度值。实验结果表明，该方法能较为准确的判断两张工序卡片的相似度，且能适用于多个领域的工序卡片。