基于数据挖掘的新冠病毒传播趋势研究*

颜蕾 杜许泞 曹建莉

(河南工业大学理学院,河南郑州 450001)

0 引言

自新冠肺炎疫情爆发以来,疫情未来发展趋势和疫情发展的影响因素成为国内外关注的焦点[1-3]。已有学者通过建立时间序列的ARIMA 模型来预测湖北省和巴基斯坦的疫情发展趋势[4-5],但从性别、年龄、人口流动等方面入手判断疫情的影响因素并利用时间序列模型进行预测的研究较少[6]。对每日新增治愈,死亡,确诊病例的研究是判断疫情未来发展趋势的重要依据,挖掘数据并对这些数据进行拟合,利用方差分析和显著性分析来进行判断,是一种重要的研究方法。另外,建立时间序列模型在短时间内可以很好地预测疫情走向。

1 回归拟合

针对疫情变化,假设天数为预测变量x,每日新增、治愈以及死亡病例分别为响应变量y1,y2,y3,建立回归模型,分析每日新增、治愈以及死亡病例的变化规律。

1.1 新增治愈

使用数据分析工具画出疫情高发期间新增治愈病例变化趋势如图1。

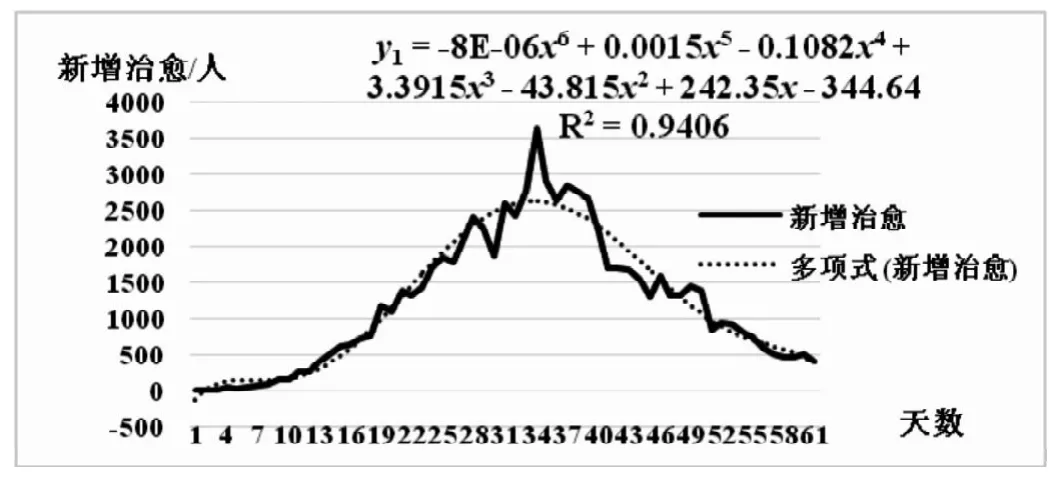
图1 新增治愈变化趋势图Fig.1 Newly added healing trend graph

其中决定系数R2=0.9406,说明趋势线拟合度极高,每日新增治愈数据的回归曲线为:

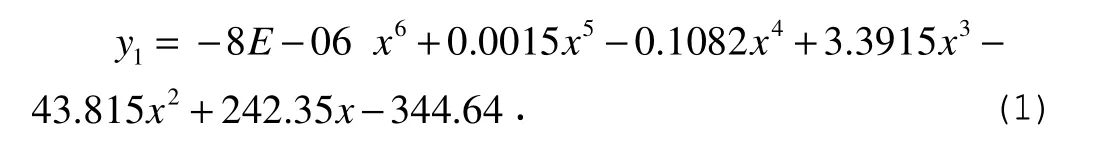
由图1可见新增治愈起初小幅增加,在第5天和第9天拐点处变化趋势不明显,之后出现迅速增长,在第36天后开始下降。

1.2 新增死亡

使用数据分析工具可得疫情高发期间新增死亡病例变化趋势如图2。

图2 新增死亡变化趋势图Fig.2 Newly added death trend graph

由图2可知,每日新增死亡人呈非线性变化,有多次波动,未见明显周期性,忽略异常离散值,可得拟合曲线为六次多项式:

其中R2=0.7983,整体拟合度较高。

图3观察拟合曲线,存在两个拐点,对拐点近似取正整数,可见每日新增死亡人数呈递增趋势,第19天(第二个拐点)达峰值,之后呈递减趋势,且速率整体持续变缓。

图3 新增死亡拟合函数与导函数图Fig.3 Newly added death fitting function and derivative function graph

1.3 新增确诊

利用SPSS软件对每日新增确诊人数进行统计得知数据离散程度较大。新增确诊绘制折线图和回归模型如图4所示。拟合指数函数为:

图4 新增确诊折线图Fig.4 New confirmed line chart

2 疫情影响因素分析

利用部分代表城市数据,并采用单因素或多因素方差分析法,检验年龄,性别以及人口迁移是否对疫情产生相关影响。

2.1 性别对疫情的影响—以信阳市为例

统计信阳市确诊病例中男女比例数据,进行性别因素的单因子方差分析,如表1所示。

表1 性别对疫情影响方差分析表Tab.1 Analysis of variance of gender impact on epidemic situation

由表中P值较小,可知性别因素对疫情影响是显著的。由95%置信区间可知,男性感染区间位于女性感染区间右侧,有较强的感染性。

2.2 年龄与性别对疫情的影响—以北京市为例

采用双因素方差分析方法,在不考虑年龄与性别交互作用情况下,探究性别和年龄对疫情是否产生影响。统计北京市确诊数据,并利用软件可得方差分析表,如表2所示。

表2 方差分析表Tab.2 Variance analysis table

由上表可知,方差分析P值均小于0.05,即性别和年龄对病毒感染均存在显著影响。

2.3 人口流动对疫情的影响—以国内数据为例

统计国内迁徙比例,检验全国人口流动对疫情感染是否存在影响。首先利用统计软件进行方差齐性检验,得到不同迁徙比率下的方差间没有明显差异。然后进行单因素方差分析,由P 值较小,说明人口迁徙比率与疫情感染有关。再进行LSD多重比较,结果表明迁徙比率0.0060与0.0061,0.0062之间无显著差异,0.0063,0.0064,0.0065,0.0066,0.0067之间无显著差异,而0.0060,0.0061,0.0062与0.0063到0.0067均有显著差异。

3 疫情预测

3.1 新增病例预测

根据SPSS建立时间序列分析,对数据进行二阶差分处理,使离散数据平稳化并同时对数据进行白噪声检验。在延迟二期之后,统计量的显著性P值都显著小于0.05,因此该数据间有关联性。预处理结束后,用SPSS对二阶差分数据创建时间序列模型预测未来变化。显著性为0.106,通过检验,可知该预测数据具有可信度。对差分后的数值进行还原,可得疫情新增人口变化,将人口数作近似取整处理,如表3所示。

表3 新增病例预测表Tab.3 New case prediction table

由表中数据可知,由于境外输入影响,新增病例会出现二次波动,但呈现递减趋势。

3.2 全球确诊病例

统计数据并绘制现存感染人数的散点图,如图5所示。

图5 全球确诊病例散点图Fig.5 Scatter plot of confirmed cases worldwide

类似于上一节方法,建立时间序列模型,其预测数据如表4所示。

表4 全球确诊病例预测表Tab.4 Global confirmed case prediction table

4 结论

本文利用统计数据研究疫情变化,分析拐点建立回归模型。新增死亡人数拟合曲线峰值远超过目前最大值,因此疫情的影响还远未结束。通过方差分析可知,年龄、迁徙比率和性别等因素都对疫情有显著影响。本文建立起时间序列模型,预测全球疫情传染仍处于危险期,感染人数仍在递增,发生二次波动的可能性较大。因选取局部抽样数据,试验结果仍存在一定偏差。