拥抱量子科技时代：量子计算的现状与前景

【关键词】量子计算  量子科技  量子信息处理

【中图分类号】G322/0413                  【文献标识码】A

【DOI】10.16619/j.cnki.rmltxsqy.2021.07.007

量子计算的概念

量子计算机是基于量子力学的基本原理，利用并发挥量子相干、量子纠缠及量子并行等特性，以全新的方式进行计算、编码和信息处理任务的设备。由于量子计算机对某些特定问题的求解具有经典计算机无法比拟的强大计算和模拟能力，可以为密码分析、气象预报、石油勘探、药物设计等所需的大规模计算难题提供全新的解决方案。例如，量子计算机的超快计算能力将极大缩短对基于计算复杂度的传统加密算法的破解时间，从而将对现有信息安全体系造成颠覆性的影响。因此，实用化量子计算机的研制成功极有可能引发一场新的科技革命。2020年10月，习近平总书记在中共中央政治局第24次集体学习中指出：“要充分认识推动量子科技发展的重要性和紧迫性，加强量子科技发展战略谋划和系统布局，把握大趋势，下好先手棋。”

量子计算的概念最早由美国物理学家R. Feynman于1981年提出[1]。Feynman预见到，量子计算机相比经典计算机更适合用来模拟量子物理系统的特性。1994年，美国物理学家P. Shor提出了首个量子算法[2]，证明量子计算机可以高效地解决大数分解问题，并可能破解广泛使用的RSA公共密钥体系，引发了全世界广泛的关注。在此后的20多年间，该领域的理论和实验研究快速发展，取得了一批令人瞩目的成就，并在某些特定领域已经发展到接近实用化的突破临界点。

此外，对量子计算的研究还可以扩展经典计算在各个领域的应用，触及量子化学、材料科学，甚至机器学习等多个交叉学科。目前，通过量子-经典混合方案[3][4]，实用化的量子辅助计算已经被应用于多种量子器件。该方案结合了经典和量子计算的优点，使用量子处理器计算系统在特定状态下的物理观测值，然后通过经典反馈优化算法。这一混合方案可用于估计分子的基态能量[5][6]，模拟量子材料[7]，以及寻找优化问题的近似解等[8]。

对量子计算的研究还极大地促进了量子信息处理技术水平的提高。我国与欧美等国都正在组建较大规模的长程量子密钥分发网络，而量子精密测量的相关技术也已经开始应用于国家安全和石油勘探等领域。虽然量子计算、量子通信和量子精密测量的侧重点和发展阶段各有不同，但都需要具有较长相干时间、且能在不同物理系統间高效转换，从而实现量子信息长程传输的量子比特存储器。这一设备不仅是实现规模可扩展的通用量子计算的核心部件，也可以用来制造下一代量子通讯网络中具有高可信度的量子中继器节点。

通用量子计算机与专用量子计算机

从设计用途角度来看，现有的量子计算机大致可以分为两类。一类是通用量子计算机，可以通过量子逻辑门电路编程，在一定误差范围内执行任意的量子算法。如IBM、Google的商用量子计算机。另一类是专用量子计算机，有时候也被称为量子模拟器，其特点为运行特定类型的量子电路，执行预先设定好的特定任务，不能通过量子门组合实现其他量子算法。如D-Wave公司推出的Ising模型量子退火机、我国的“九章”波色采样量子专用机等。

通用量子计算机的主要发展目标为容错量子计算，容错量子计算的核心问题在于实现尽可能多的可以自己检测错误与纠正错误的、具有自我保护功能的容错计算单元，该计算单元一般被称为逻辑量子比特。与之相对应，不具有完整容错功能的计算单元，一般被称为物理量子比特。为了实现逻辑量子比特，目前主要有两种思路，一种是在物理量子比特基础上，通过进一步提高操作保真度，减小逻辑门的操作与测量误差，或者引入大量的冗余辅助物理量子比特与合适的量子纠错编码算法，来逐步逼近直至实现逻辑量子比特。另一种思路是从基础材料的研究出发，寻找具有特殊容错性质的新型量子计算载体，如基于马约拉那费米子的拓扑量子计算方案。

目前已经搭建完成的通用量子计算设备主要由物理量子比特构成。其最重要的参数是可用于编程的量子比特数目，以及在一定误差范围内可连续执行的量子逻辑门数目。目前有两种指标可用来度量一个通用量子计算机的计算能力：量子体积（由美国IBM公司提出）或算法量子比特数（由美国IonQ公司提出）。算法量子比特数是指可用于实现量子算法的量子比特数目。量子体积是指“设备在给定的空间和时间内完成的量子计算的有用量”。影响量子体积的因素有很多，包括量子比特数量、设备连接度、相干时间、逻辑门操作和测量误差、设备串扰以及量子电路软件编译器效率等。量子体积越大，量子计算机可能解决的实际复杂问题就越多。

在算法方面，量子计算被认为可以在两类重要的问题中表现出相对经典计算机的显著加速，包括量子搜索型算法和量子隐藏子群型算法。它们的典型代表分别为Grover算法与Shor算法。另外有一些算法——如量子计数算法——可以同时属于这两类。理论研究表明，Grover算法对于无结构搜索问题具有平方加速，并且很容易通过定义映射来解决诸如数独等实际问题。此外，Grover算法的迭代振幅放大搜索过程具有鲜明的几何意义，易于进一步分析与优化，因此，在理论量子计算研究中有着重要地位。Shor算法在解决大整数分解问题时，相比于目前已有的所有经典算法，都具有指数级的加速。而大整数分解的困难性是目前绝大多数非对称加密算法的基础。在非对称加密算法中，公钥和加密信息都可以在公开信道中发布，而只有持有私钥的特定收信人才能正确的解密信息。因此，这一类算法是目前基于公共网络（非专线）进行加密通信最重要的方式。目前常用的非对称加密算法——如RSA算法——多利用大整数分解的困难性。因此，Shor算法的实现可能让公共网络中的加密通信变得不再安全。假如，某国家或组织通过Shor算法实现了对目前RSA算法的高效破解，就可以肆意窃听所有利用该算法加密的公共网络通讯。因此，能运行大规模Shor算法的量子计算机一旦研制成功，必然会成为颠覆现有网络通信构架的信息“核武器”。这也是许多国家大力发展量子计算机的一个重要原因。

如果说Shor算法是一柄锋利的矛，可以刺破各种经典加密通讯，那么量子通信则是一块不可突破的盾，可以在量子算法的破解下依然保证无条件安全。我国在早期就开始大力发展量子通信产业。目前，基于光纤的量子保密通讯已经实际用于各政府、银行、企业的关键信道加密，基于“墨子号”卫星的空天量子中继保密通讯更是远远走在了国际前列。因此，即使在不远的未来有人能研制出能够运行大规模Shor算法的量子计算机，我国也仍然能保证关键通讯的安全性。

通用量子计算机以量子比特和量子门作为基本计算单元。与经典比特相比，量子比特可以处于0和1之间的任意一个叠加态。根据量子力学的基本原理，当这样的叠加态通过一个量子门时，作用的结果也会自动线性叠加，而并不需要人为地去把叠加态系数展开，分别计算再重新叠加起来。这种利用量子态叠加等原理的计算方案，可以实现量子态层面的指数级并行计算加速。但是，由于量子态表征的只是概率分布的概率幅，如果将实际问题中确定性的输入和输出直接与量子态进行映射，本身就需要指数级复杂度的输入（态制备）操作与输出（测量）操作。这样一来通用量子计算机的速度优势就被完全消解了。所以绝大多数具有实用价值的量子算法都要经过精心设计，使得问题的输入输出并不和量子态直接对应，而是利用量子态测量的特殊性质，构造出类似于干涉的计算过程，将原始问题的求解转化为对干涉条纹位置的测量，以及相应的后续处理。目前来看，通用量子计算机主要擅长解决搜索类型的问题，能够在某些经典计算机计算困难的搜索问题上实现平方级甚至指数级的加速。值得注意的是，这里指出的“搜索”是广义的概念，既包括通常意义上无结构数据库的搜索（原始Grover算法），也包括函数或者矩阵解空间的搜索（量子本征值求解算法，机器学习HHL算法，及基于变分法的量子化学VQE算法等），甚至还包括抽象的特殊性质子群或者整数因子的搜索（量子傅立叶变换，Shor算法等）。这些不同类型的搜索具有一个共同的特点，就是问题的输入（待搜索空间的描述）和输出（搜索结果）规模相对较小，而找到解的过程对于经典计算机却是非常困难的。通俗来讲，这类问题可以类比为走迷宫，求解就是寻找能走出迷宫的正确路径，而量子计算机可以利用量子并行性高效地找到这些正确路径。

通用量子计算机擅长解决搜索类的问题，并不是说通用量子计算机不“通用”。首先，通用量子计算机具有完整的通用计算能力。他可以通过量子Toffoli门的组合，实现所有经典可实现的计算，并能实现经典计算完成不了的可逆计算。从信息熵的角度来说，只要计算过程不可逆，就必然会产生发热。因此，相比于经典计算机，通用量子计算机在计算理论研究领域具有极大的价值和优势。其次，通用量子计算机所擅长的广义搜索问题其实涵盖了很大一部分计算问题。最后，通用量子计算机的通用性还表现在，仅通过一组有限集合中的通用量子逻辑门的有限长度组合，我们就可以實现——或者以任意精度逼近——任意的量子逻辑门操作。这个发现从理论上保证，人们只需要集中精力研究实现一小组通用量子逻辑门，就可以实现任意的通用量子计算。这一点与经典计算机的构建过程类似，即从最基本的晶体管和最简单的逻辑门电路出发，逐级从底层向上，直至构建出各种复杂的应用程序帮助人们解决实际问题。

关于专用量子计算机或者量子模拟器，已经有理论指出，任何只存在局域性耦合的专用量子计算机都可以通过通用量子计算机进行高效地实现[9]。因此，现有的专用量子计算机主要有两种发展思路。第一，针对本身就需要非局域性或者全局耦合的特定问题或者量子算法进行设计。这类问题或者算法暂时无法在通用量子计算机上得到有效地实现，所以只能依靠专用量子计算机。例如，在具有长程相互作用的量子多体系统的模拟问题中，由于任意两个粒子之间都存在相互作用，在代入量子力学方程中求解时，必须要对整个稠密的态空间进行求解。而根据量子力学基本原理，该系统的整体态空间是通过各成分粒子的态空间直积展开得到的，因此，整体态空间的维度将随着粒子数指数增长。举个直观的例子，对于一个由300个单自旋粒子组成的小规模系统，其态空间的维度已经高达2^300～10^90，远远超过了可观测宇宙中所有原子的数目（10^80）。因而，现有的计算手段都必须借助一些体系的特殊性质进行部分近似后在统计层面求解，并不能做到基于第一性原理的精确求解。在Feynman最初提出量子计算机的概念与设想时，他的主要动机之一就是解决这类模拟问题。事实上，Feynman说到，“自然界是量子的，那我们只能拿量子计算机去模拟它”。专用量子计算机的第二个发展思路，是在同等技术水平或成本要求下，通过牺牲一部分通用性换取更高的计算性能，从而能针对某些特定类型的问题实现更高效的计算。因此，专用量子计算机研究的关键在于提高可解决问题的规模，以及寻找将更多有意义的实际问题关联到专用模型量子电路的映射。

量子“优越性”

所谓量子“优越性”（Quantum supremacy，也被翻译为量子“霸权”），最初只是一个理论计算机复杂度的提法，原意是指在量子计算机上演示完成一项具有显著量子加速的任务[10]。这里所说的“显著量子加速”具有非常高的理论严格性，指的是对于某个特定问题，我们可以严格证明量子计算机将确定性地显著超越（至少指数加速）所有经典算法。这里的经典算法既包括已经发现的算法，也包括尚未发现的算法。或者说，我们需要找到一个问题，先从数学上严格证明其经典算法的算法复杂度，再找到一个量子算法，并证明该量子算法对所有经典算法都存在至少指数级加速。

与之前提到的一些量子算法的例子相比，量子“优越性”问题主要有两点不同。第一，前文中的一些问题并没有严格地数学证明其经典算法复杂性。例如，虽然目前所有的经典算法在计算大整数分解问题时都非常困难，但我们也不能否认高效经典算法存在的可能性。换句话说，有可能存在某个尚未被发现的大整数分解经典算法，可以和量子计算机上的Shor算法一样快。因此，严格说来，我们只能说Shor算法很高效，但不能说他具有量子“优越性”。第二，用于演示量子“优越性”的问题不需要具有任何实际意义。这个问题完全可以是人为构造的，只是为了证明经典计算机在某些情况下一定不如量子计算机。其他的复杂问题未必可以、通常也很难归约到这个人造问题。因此，我们需要辩证地认识和理解量子“优越性”。量子“优越性”的成功演示，能够说明量子计算机具有经典计算机所不具备的计算能力，代表了我们认识上的巨大进步。同时也要清醒地看到，量子“优越性”并不能直接地转化为求解实际问题的能力，而且这个转化甚至可能永远都没法完成。例如，Google公司在展示量子“优越性”时采用的量子随机电路模拟问题，以及我国“九章”量子专用机采用波色采样模拟问题，目前都无法直接和具有应用价值的实际问题建立联系。

通用量子计算机的物理实现

目前，可进行量子计算实验研究的物理系统主要包括超导量子器件、离子阱、光子系统、量子点、金刚石色心、冷原子气体、核磁共振系统，以及仍处于理论研究阶段的拓扑量子系统等。这几种系统在不同的问题研究中各有优势，也都存在亟待解决的关键难点。对于如何判定一种物理系统是否可用来实现通用量子计算，国际上一般使用DiVincenzo判据。该判据由D. P. DiVincenzo最早提出[11]，主要包含五个条件。

一是物理系统需要具有可掌控的量子比特，并具有可扩展性（A scalable physical system with well characterized qubits）。“可掌控的量子比特”是指我们不仅能够在物理上实现量子比特，且该量子比特的物理参数、与其他量子比特的相互作用，以及与环境的相互作用都能够被确定性地描述。“可扩展性”是指能够实现的量子比特数量要具有一定的规模。拥有几百到上千个量子比特的量子计算机才真正具有比经典计算机优越的性能，且其中所有的量子比特之间应当能够互相分辨、单独操作，且可以从整体上完全掌控它们的行为。

二是能够将量子比特初始化到一个简单的量子态（The ability to initialize the state of the qubits to a simple state）。这个条件包含两方面的要求。第一，是量子计算机能够被初始化。量子计算机应该能重复使用，在开始新的量子计算任务之前必须将所有量子比特置于一个己知的态。第二，要能够满足量子纠错的要求，即在计算过程中可以源源不断地提供“空白”的量子比特。

三是能在较长时间内保持量子相干性，或者说退相干时间要远大于量子逻辑门的操作时间（Long relevant coherence time， much longer than the gate operation time）。量子比特与环境的耦合会导致其量子相干性的丧失。人们通常把量子比特退相干时间与量子逻辑门操作时间的比率称为品质因子。要实现任何具有实际意义的量子算法，都需要量子计算机的品质因子远远大于一。

四是能够进行普适的量子逻辑门操作（A universal set of quantum gates）。任意的量子幺正操作都可以通过一组普适量子逻辑门来实现。因此该条件保证了该量子计算机可以完成任意的量子计算任务。

五是能够进行单量子比特的测量（A qubit specific measurement capability）。这个条件对应于量子信息的读出。

除以上五条外，D. P. DiVincenzo后来又添加了两条关于实现量子计算机网络的要求，即本地量子比特和飞行量子比特能够互相转化（The ability to interconvert stationary and flying qubits），以及能够在两地间传播飞行量子比特（The ability to faithfully transmit flying qubits between specified locations）。

上述两条要求与量子网络的研究密切相关。量子网络与量子计算是量子信息科技里两个相对独立而又联系紧密的研究分支。二者之间的关系类似于互联网和计算机的关系。

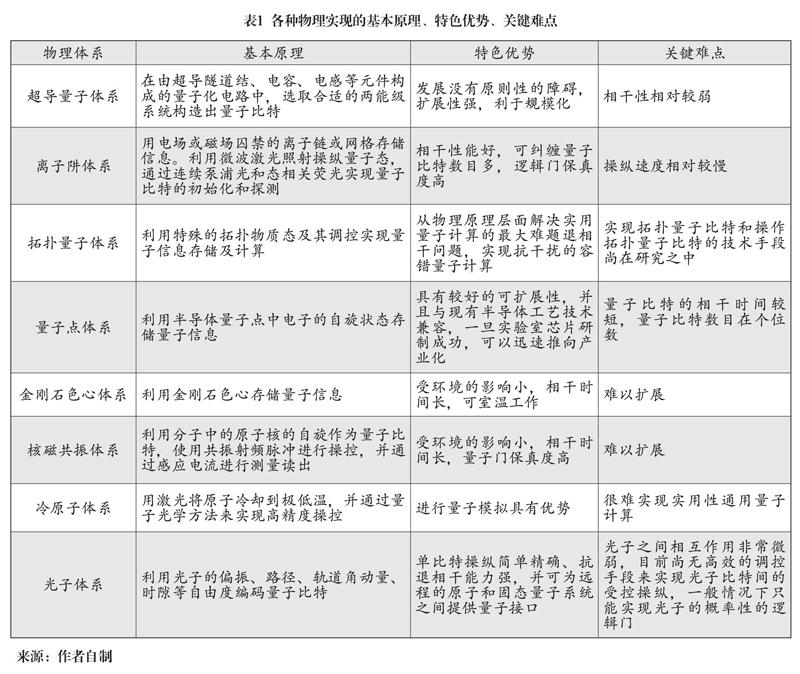
虽然DiVincenzo判据理解起来比较直观，但要找到一个可以满足全部判据的实际物理系统却并不容易。从技术層面看来，有些判据甚至是相互矛盾的，在设计系统时需要非常仔细地寻找合适的平衡点。例如，延长相干时间需要量子比特尽量“与世隔绝”，而幺正操作和强测量又要求量子比特能与量子门和探测器很好的“交流”。从DiVincenzo判据出发，我们在下表中逐一分析了各种物理实现的基本原理、特色优势，以及关键难点。

国内外研究现状

整体发展态势。鉴于量子计算机强大的运算和海量数据处理能力，美国、欧洲和日本等发达国家政府以及国际知名科技公司如Google、Intel、Microsoft和IBM等都发起研究计划，斥资研发量子计算机。从上世纪90年代起，美国的多家机构如国防部高级研究计划局（DARPA）、能源部、国家科学技术委员会（NSTC）等先后启动了量子科技相关规划。2016年7月，美国国家科学技术委员会发布题为《推进量子信息科学：国家的挑战与机遇》的报告，重点强调发展量子计算的重要性。2018年，美国国会众议院通过《国家量子倡议法案》。同年，美国政府在白宫举办量子峰会，并发布了《量子信息科学国家战略概述》。2020年，白宫国家量子协调办公室发布《美国量子网络的战略构想》和《量子前沿：量子信息科学国家战略进展报告》，进一步确立了美国在该领域开展国际对抗性博弈的发展战略。目前，美国联邦政府支持量子信息科学的研发投入每年为2亿美元左右。此外，多家科技公司在量子领域的投资也大幅提高。欧盟委员会于2016年发布《量子宣言：量子技术旗舰计划》，拟在10年间投入10亿欧元，进行量子通信、量子模拟、量子传感和量子计算机方面研究。2018年，该计划得到了进一步细化，并在基础量子科学和云计算领域进行了扩充。

我国在量子信息领域的研究起步晚于美国，但在国际上较早形成了战略部署和发展规划，因此在进入21世纪以来基本保持在第一梯队。2006年，《国家中长期科学和技术发展规划纲要（2006～2020年）》将量子调控列入四个重大基础研究计划。2015年，“十三五”规划进一步加强了对量子通信和量子计算领域的布局。2021年，《“十四五”规划和2035年远景目标纲要》将量子信息确立为具有前瞻性和战略性的国家重大科技项目，并提出了“加快布局量子计算、量子通信、神经芯片、DNA存储等前沿技术”的要求。目前，我国在量子计算领域的研究水平整体上依然处于跟跑状态，但已经形成了一个颇具发展潜力的研究队伍，在主要的物理平台完成了全面布局，并在部分方向实现了突破。

超导量子计算机。（1）国际主要团队和现状。超导量子计算机方案是目前国际进展最快的方案。国际上绝大部分研究机构都在美国和欧洲，其中比较有代表性的研究组有：美国的加州大学圣巴巴拉分校、耶鲁大学、麻省理工学院、美国国家标准局（NIST）、加州大学伯克利分校、马里兰大学、芝加哥大学，以及荷兰的代尔夫特大学（Delft）、瑞士的苏黎世联邦理工学院（ETH）、日本的理化研究院等。此外，还有Google、IBM、Intel、D-wave、Rigetti为代表的20多家公司也积极参与该方向的研究。

目前，通用超导量子计算机的研制仍然处于初期的阶段，主要围绕提高广度和深度两个方面开展工作。广度是可控耦合量子比特的数目，目前国际已发表的文献中最好水平大约是20个。深度是指可以连续进行的高保真度多量子比特逻辑操作次数。对于20比特的广度，当前最好的深度能达到40次左右。要实现实用化量子计算，广度和深度必须同时提高、相互配合。按照理论估计，当达到50个比特50次操作以后，量子计算机的性能将接近甚至超越目前最快的经典计算机。这样的指标有可能在3到5年内实现。

（2）国内主要团队和现状。我国在超导量子计算的实验研究上起步较晚，但是近几年通过科技部、基金委、教育部以及地方政府等相关项目的实施，培育出一批优秀的团队并做出了一些亮点性工作，如浙江大学、中国科学院物理研究所、中国科学技术大学三个单位联合开展的十个超导量子比特的纠缠，清华大学在基于谐振腔光子态的量子纠错演示，以及近期南京大学研发的超导量子模拟器等。在指标方面，我国各研究组均在快速提升。目前已发表的文献中报道的广度为20左右。从事超导量子计算的实验研究团队有：清华大学、浙江大学、南京大学、中国科学技术大学、南方科技大学、中国科学院物理研究所和北京量子信息科学研究院等。此外，阿里巴巴、腾讯、百度、华为、浪潮等科技公司也注意到超导量子计算的应用价值和发展潜力，纷纷设立相应的研发部门进行攻关。

就整体水平而言，我国与欧洲（如德国、法国、瑞士和荷兰）和日本处在同一水平线，在部分方向略微超前。与美国的顶尖研究组相比（如耶鲁大学、Google、IBM、麻省理工学院），虽然由于起步较晚，积累不足，存在一定差距，但这个差距并没有形成代差，以现在的研究进展速度衡量，约有三年左右。在正视差距、准确定位不足的条件下，如果合理选择技术路线和研究方法，通过战略布局重点攻关，中国完全具备超车的条件。

离子阱量子计算机。（1）国际主要团队和现状。离子阱系统和超导系统是美国政府资助最多的两个量子计算研究方向。除通用量子计算机以外，离子阱还被广泛应用于量子化学、相对论量子力学、量子热力学等领域的量子模拟研究。由于离子阱在量子物理学，特别是量子计算与量子模拟上的重要意义，发明离子阱的W. Paul获得了1989年的诺贝尔物理奖，第一次把离子阱技术用于演示量子计算的D.Wineland获得了2012年的诺贝尔物理奖，首次提出基于离子阱量子计算理论方案的I.Cirac和P.Zoller获得了2013年Wolf物理奖。

在国际上，从20世纪90年代初人们首次尝试将离子阱用于量子计算开始，离子阱量子计算的实验研究已经过二十余年的发展。早在2011年，奥地利因斯布鲁克大学R.Blatt实验组就基于M?lmer-S?rensen方案实现了14个离子量子比特的Greenberger-Horne-Zeilinger纠缠态的创建。2016年，英国牛津大学D.M.Lucas实验组使用在室温离子阱中钙43离子的超精细结构作为量子比特，实现了保真度分别为99.9%的两量子比特门和99.9934%的单量子比特门，显著高于容错量子计算所需的99%最小阈值。最近该实验组实现了亚微秒级别且不受囚禁频率限制的多离子量子门，大大缩小了离子阱系统与超导系统在量子操作速度上的劣势。2016年，美国马里兰大学C.Monre实验组展示了一个五量子比特囚禁离子量子计算机，该计算机可以通过执行任意通用量子逻辑门序列来实现任意的量子算法。他們将算法编译成完全连接的一组硬件门操作，达到了98%的平均保真度，并在此基础上实现了Deutsch-Jozsa和Bernstein-Vazirani算法，以及大数分解Shor算法的核心步骤量子傅里叶变换。最近他们还通过引入低温制冷技术，在单个离子阱中成功稳定囚禁超过100个离子（44个可寻址），并研制出含有53个量子比特的量子模拟器。

（2）国内主要团队和现状。国内对于离子阱量子计算机的实验研究只有不到十年的历史，研究团队主要分布于清华大学、国防科技大学、中国科学技术大学、中科院精密测量院（原中科院武汉物理与数学研究所）、中国人民大学、中山大学等。2017年，清华大学交叉信息研究院研究团队实现了四个离子量子比特的高保真度任意操控，达到世界一流水平。该团队还成功实现相干时间超过10分钟的单个量子比特，是迄今为止单量子比特相干时间的世界纪录，将之前的世界纪录提高了10倍。总体而言，国内大部分实验组仍处于一到两个比特的初期研究阶段，水平有待进一步提高。但是，国内部分团队从离子光频标钟精密测量方向发展而来，具有成熟的自主实验技术基础。且研究团队负责人大多拥有国外一流研究组研究经历，起点高发展快，具备在3到5年内追赶上国际一流水平的条件。

拓扑量子计算机。（1）国际主要团队和现状。微软公司是国际上拓扑量子计算方案的主要推动者。2005年，该公司成立专门从事拓扑量子计算研究的Station Q研究所，并长期高额资助了世界上多个顶级的实验室主攻拓扑量子计算科学与技术，如荷兰代尔夫特理工大学Kouwenhoven研究组和丹麦哥本哈根大学Marcus研究组等。目前，包括美国加州大学洛杉矶分校的王康隆研究组在内的多国实验室均发现了可以构筑拓扑量子比特的量子态迹象。微软公司称有望在1到2年内实现拓扑量子比特。

（2）国内主要团队和现状。拓扑量子计算的基础是对拓扑量子物态和效应的研究。我国近年来在该领域取得了重大进展，整体具备世界一流水平，在某些方向处于国际领先地位。例如，清华大学的薛其坤团队及其合作者在世界上首次实现了量子反常霍尔效应，在界面超导方面居世界领先地位，在基于量子反常霍尔效应的量子计算研究方向确立了技术优势和材料优势。上海交通大学的贾金锋团队在拓扑量子计算所需材料的生长上有深厚积累和国际重要成果。北京大学的杜瑞瑞团队是量子自旋霍尔效应的国际学术领导者，该体系的拓扑特性稳定，适合开展量子计算相关研究，并且目前的技术准备相对成熟。此外，我国在半导体纳米线和分数量子霍尔效应等领域也开展了拓扑量子计算的国际前沿研究。与其他量子计算的系统不同，拓扑量子计算是个困难前置的方案，其实现的最大瓶颈在于拓扑量子比特的物理实现。从这个角度讲，国内和国际的研究均刚刚开始，处于齐头并进的态势。

半导体量子点量子计算机。（1）国际主要团队和现状。美国休斯研究院、美国普林斯顿大学、澳大利亚国家量子计算与通信技术研究中心、荷兰代尔夫特大学和日本东京大学等均实现了半导体两量子比特的逻辑门操控，其中荷兰代尔夫特大学研究组同时实现了量子算法演示，并已开始利用产业生产线进行8寸大小的工业尺寸的半导体量子芯片制造。同时Intel公司和法国CEA-Leti实验室也开始致力于半导体量子芯片制造核心工艺技术的研发。

经过近十年的发展，国际半导体量子计算研究领域已经将获得高质量长相干时间的量子芯片材料体系作为量子芯片研发的核心任务之一。世界范围内以美国、澳大利亚和欧洲为代表，均专门设立了半导体量子芯片材料生长和表征团队，为国家层面的半导体量子计算研究提供统一的量子芯片材料，特别是进入到硅纯化的量子芯片材料生长阶段，其材料生长工艺技术和材料性能已经完全不公开。

（2）国内主要团队和现状。国内半导体量子点量子计算机的实验主要在中国科学技术大学的量子信息重点实验室和北京大学开展。中国科学技术大学团队在电荷量子比特方向先后实现了单、双和三个量子比特的制备与逻辑门，完成了半导体量子比特逻辑单元库的建立，同时利用微波谐振腔实现了多量子比特的扩展架构，为规模化量子芯片研制奠定了坚实基础。研究整体处于并跑状态，在材料和测量设备环节受控于国外技术，处于跟跑状态。北京大学的徐洪起团队在半导体量子点自旋量子比特的研究中，深入研究了线性多量子点中的电荷与自旋量子態的构型，实现了单电子的远距相干传输，为发展与当代半导体技术工艺兼容的量子计算芯片技术奠定了基础，成果处于该领域国际领先地位。

高质量硅基半导体量子芯片材料是半导体量子计算研制的核心材料基础，我们必须开展专门的半导体量子芯片材料生长、表征和器件测试等相关工艺和技术开发，获得未来量子芯片制造的核心工艺技术，为半导体量子芯片制造和未来量子计算机的研制奠定坚实的材料基础。同时，国际半导体量子计算研究已经到了大量工程技术和产业界进入的新阶段，国内整体还处于实验室阶段，需要加大工程技术和产业的投入以期加速量子计算机的研制进程。

金刚石NV色心量子计算机。（1）国际主要团队和现状。2008年，德国斯图加特大学Wrachtruo研究组和美国哈佛大学Lukin研究组同时实现了NV色心在纳米尺度检测直流和交流磁场的技术，是NV色心在量子精密测量领域的首次应用。2012年，荷兰代尔夫特技术大学Hanson研究组在NV色心系统中实现了Grover算法的演示。同年，多个研究组报导了利用NV色心对弱耦合C-13的探测和相干控制，将NV色心体系可控制量子比特扩展到3-6比特。2014年，Wrachtrup研究组和Hanson研究组实现了NV色心系统中的三比特量子纠错算法演示。同年，Wrachtrup研究组利用最优化控制方法，在NV色心系统中实现了高保真度纠缠态制备。2015年，Hanson研究组利用光学手段将相距1.3km的NV色心纠缠起来完成了Loophole-free Bell不等式检验，并于2017年实现了NV色心系统中的纠缠态。2018年，Hanson研究组在低温条件下将NV电子自旋相干时间延长到秒量级，并探测到19个与NV耦合的C-13核自旋。

（2）国内主要团队和现状。近年来，国内在NV色心量子计算的研究方向进展良好。2010年，中国科学技术大学杜江峰研究组在NV色心系统中实现了Deutsch-Jozsa算法演示，并于2017年实现了大数分解算法演示。2013年，中科院物理所潘新宇研究组在NV色心系统中演示了基于动力学解耦的逻辑门控制方法。2014年，清华大学段路明研究组在NV色心体系中演示了和乐量子计算。2015年，杜江峰研究组完成了NV色心中单比特保真度0.999952和两比特保真度0.992的量子控制，创造了当时量子系统的最高纪录。2018年，清华大学龙桂鲁研究组利用与平均哈密顿量理论相结合的最优化控制理论，去除了环境演化对量子控制的影响，首次在NV弱耦合系统中实现了最优化控制。

另外，我国在NV色心的其他研究领域——如光学方法耦合等方向的发展——落后于国际最高水平。NV色心体系中需要用到的高品质样品（低N杂质样品）及高品质实验仪器（高带宽任意波形发生器、高频率微波源、高带宽示波器）严重依赖进口。现有的NV色心单比特控制的保真度已达到0.9999，超过了量子纠错阈值。未来通过进一步发展控制方法，改进电子仪器的精度，我们有望实现两比特以上操控的高保真度控制，并借助量子纠错算法实现量子逻辑比特。此外，借助光学微腔等光学结构还可以增强NV色心发射光子的接受率，提高NV色心之间的耦合强度，并实现量子网络。

核磁共振量子计算机。（1）国际主要团队和现状。核磁共振体系由于具有成熟的脉冲控制技术、长相干时间等优点，是量子算法演示、量子系统模拟和量子控制方法检验的重要平台，其发展出的控制方法有望方便地移植到其他量子体系中。国际上从事核磁共振量子计算的研究机构包括加拿大滑铁卢大学，德国多特蒙特大学、英国牛津大学、印度理工大学等。该体系中目前可实现的量子比特数目可达12个。该记录由加拿大滑铁卢大学和清华大学联合完成。

（2）国内主要团队和现状。清华大学龙桂鲁研究组和中国科学技术大学杜江峰研究组处于国际领先水平。其中清华研究组不仅率先演示了包括和乐量子算法等重要实验，发展了反馈控制优化算法，而且利用核磁共振体系来优化对自身系统的控制，提高了速度和精度。2017年10月，清华大学推出了国际上第一个基于核磁共振的量子云平台，引起国内外的广泛注意和报道。中科大研究组利用核磁共振系统完成了大数分解、H原子能级模拟、凝聚态体系量子模拟等重要的量子算法演示和量子模拟实验。

冷原子量子计算方案。（1）国际主要团队和现状。美国几乎所有顶尖大学的物理系都设有冷原子实验研究小组，欧盟在这方面也投入很大。从2007年开始，美国国防部高等研究计划局（DARPA）开展了为期五年的“光晶格量子模拟”项目，资助了美国最优秀的团队和部分欧洲一流团队，促进了技术发展。该计划的后续效应一直延伸到近两年所取得的一些突破性进展，超越经典计算能力的量子模拟初露端倪。2017年，哈佛大学研究组在80个格点的系统中模拟了强关联的费米子模型。这类量子模型被认为是理解高温超导等新奇量子特性的关键模型。2018年，哈佛大学和麻省理工学院的联合研究组实现了基于冷原子体系的51比特可编程量子模拟机，模拟了一类量子问题的动力学行为。

（2）国内主要团队和现状。冷原子物理是一个需要长期技术积累的研究方向。我国大规模的冷原子物理研究起步较晚，但近十年来，随着投入的增加，已经建成了多个比较成熟的冷原子物理实验室，掌握了绝大多数关键技术，少数最新技术也在积极跟进当中。中国科学技术大学、山西大学、香港科技大学、中国科学院武汉物数所等多家单位近年来在自旋—轨道耦合效应的量子模拟实验研究中处于国际领先的并跑位置。清华大学实验组近期实现的超过1万个原子的量子纠缠，在精密测量上具有重要的应用前景。一个需要重视的现状是目前国内冷原子实验的关键仪器和设备都购自欧美。特别是高性能激光器、光电控制和探测仪器等，需要在国家层次上协调大力扶持发展。在国家保持稳定充足支持的情况下，我们可以在十年内跻身第一集团。

光学量子计算机。（1）国际主要团队和现状。国际上光量子计算的主要研究团队分布在维也纳大学量子科学与技术研究中心、美国麻省理工学院电子研究实验室、英国布里斯托大学量子光学研究中心、澳大利亚昆士兰大学量子计算与量子通信技术研究中心等科研机构。光量子计算的研究焦点主要集中包括单光子源和多光子纠缠源在内的量子光源，以及用于调控光量子比特的量子线路。

（2）国内主要团队和现状。作为国内开展光量子计算的主要团队，中国科学技术大学研究组长期以来开展了系统性和战略性的研究，取得了一系列重要成果：在国际上首次实现五、六、八、十光子纠缠，始终保持着光子纠缠态制备的世界纪录，同时制备了国际上综合性能最优的单光子源，开展了光子逻辑门、容失编码、拓扑量子纠错、多自由度隐形传态等面向可扩展量子计算的研究，首次实现了Shor算法演示、任意子分数统计的量子模拟、求解线性方程组量子算法和量子人工智能算法等，在光學量子计算领域一直保持着国际领先地位。此外，南京大学和北京大学的研究组各自在光子芯片的研究中取得突破;山西大学研究组在连续变量光量子计算研究中也获得一些进展。在量子光源的研究中，我国处于国际领先水平;在量子线路，特别是集成光量子线路的研究中，与国际最先进水平尚有一些差距。

近期发展趋势

鉴于量子计算机强大的运算能力和在军事国防、金融、信息安全、灾害预报等领域的潜在应用价值，量子计算机的研发势在必行。目前，美欧日等发达国家的政府、高校、公司，以及各种机构都纷纷介入研发，抢占科技制高点，在此方向的国际竞争已经到了白热化的阶段。

以目前的国际研究态势，实现具有容错能力的通用量子计算机还很遥远，如果没有重大理论技术创新，短期内很难真正实现。但是，能够展示量子加速效应的专用量子计算机有可能在3到5年内问世。这种专用量子计算机在某些特定的算法上能够超越目前最快的经典计算机，实现所谓的量子“优越性”，并在一些实际问题的求解中展现出应用潜质。

由于我国在量子计算机软硬件的研究上起步比较晚，研究基础相对薄弱。特别是实验条件和人才队伍是这十几年慢慢培养起来的，对实现量子计算机这个复杂的系统工程来说，暂时不能满足和发达国家全面竞争的需要。但是这个差距并没有完全拉开，在实用化量子计算机的这场国际马拉松竞赛中，中国和欧美发达国家都处于起跑阶段。依靠和发挥我国长期积累的、在物理和材料等学科的研究基础优势，并把这些优势转化成推动力，外加合适的科技政策引导，我国有望赢得这场颠覆性的科技竞赛。

注释

[1]Feynman， R. P.， "Simulating physics with computers"， Int. J. Theor. Phys.21， 1982， pp. 467-488.

[2]Shor， P. W.， "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer"， SIAM J. Comput.26， 1997， pp. 1484-1509 .

[3]McClean， J. R.; Romero， J.; Babbush， R. & Aspuru-Guzik， A.， "The theory of variational hybrid quantum-classical algorithms"， New J. Phys.18， 2016， 023023.

[4]Peruzzo， A.， et al.， "A variational eigenvalue solver on a photonic quantum processor"，  Nat. Commun.5， 2014， pp. 1-7.

[5]Shen， Y.， et al.， "Quantum implementation of the unitary coupled cluster for simulating molecular electronic structure"，  Phys. Rev. A95， 2017， 020501.

[6]Kandala， A.， et al.， "Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets"， Nature 549， 2017， pp. 242-246.

[7]Bauer， B.; Wecker， D.; Millis， A. J.; Hastings， M. B. & Troyer， M.， "Hybrid Quantum-Classical Approach to Correlated Materials"， Phys. Rev. X6， 2016， 031045.

[8]Farhi， E.; Goldstone， J. & Gutmann， S.， "A Quantum Approximate Optimization Algorithm"， ArXiv14114028 Quant-Ph， 2014.

[9]Lloyd， S.， "Universal Quantum Simulators"， Science 273， 1996， pp. 1073-1078.

[10]Aaronson， S. and Chen， L.， "Complexity-Theoretic Foundations of Quantum Supremacy Experiments， ArXiv161205903 Quant-Ph， 2016.

[11]DiVincenzo， D. and IBM.， "The Physical Implementation of Quantum Computation"， Fortschritte Phys. 48， 2000.

责 编/马冰莹

张威，中国人民大学物理学系教授、博导。研究方向为超冷量子气体、量子信息与量子计算、强关联电子体系。主要著作有《Towards quantum simulation of Sachdev-Ye-Kitaev model》《Experimental Determination of PT-Symmetric Exceptional Points in a Single Trapped Ion》等。