量子计算及其哲学意义

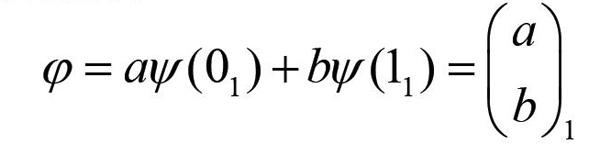
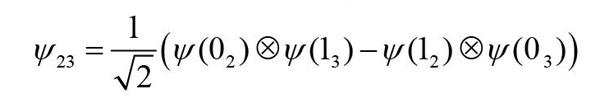
【关键词】量子计算  量子信息  量子实在 量子优势  哲学

【中图分类号】N031                               【文献标识码】A

【DOI】10.16619/j.cnki.rmltxsqy.2021.07.003

量子科技是当代最重要的核心科学技术之一。近年来，美国、德国、英国、法国等西方科技强国纷纷对量子科技加大研发投入。2016年英国启动“国家量子技术专项”，2018年德国发布“量子技术——从基础到市场”研究框架计划，2018年美国出台“国家量子行动法案”，2021年法国启动量子技术国家战略。我国对量子科技的发展与应用高度重视。习近平总书记在2020年10月中央政治局第二十四次集体学习时高度强调推进量子科技发展的重大意义。他指出：“量子科技发展具有重大科学意义和战略价值，是一项对传统技术体系产生冲击、进行重构的重大颠覆性技术创新，将引领新一轮科技革命和产业变革方向。”[1]2021年3月发布的“十四五”规划纲要提出，要“瞄准人工智能、量子信息、集成电路、生命健康、脑科学、生物育种、空天科技、深地深海等前沿领域，实施一批具有前瞻性、战略性的国家重大科技项目”，“加快布局量子计算、量子通信、神经芯片、DNA存储等前沿技术”。量子计算是量子科技的重要内容，量子计算也是一个已部分解决，还亟待完全解决的重大科技问题。本文将论述量子计算的源起、量子计算的性质、量子信息与量子实在的关系、量子计算对复杂性的意义以及哲学与发展量子科技的关系。

量子计算的源起

20世纪诞生的计算机极大地推动了科技、经济和社会的发展，推动了信息社会的形成。目前的计算机是经典计算机，其核心是经典计算。从物理学来看，经典计算就是经典物理系统按照经典物理学的规律对输入的经典信息进行处理，并输出处理结果。按照摩尔定律，计算机芯片的集成度每18个月将翻一番。当集成电路线宽小于0.1微米时，量子效应将影响电子运动，只有利用量子理论才能解决这一问题。20世纪80年代，物理学家费曼（R. P. Feynman）率先推测，按照量子力学规律运作的計算机（量子计算机）可能解决这一问题。

1993年，本内特（C. H. Bennett）等6位科学家联合在《物理评论快报》发表题为《经由经典和EPR[2]通道传送未知量子态》的论文，直接引发了量子信息理论的研究。1997年，中国科学技术大学潘建伟等合作完成的量子隐形传态实验发表在《自然》杂志上，[3]标志着量子信息理论在实验上成功实现。

自20世纪量子力学诞生以来，人们总在寻求利用量子效应来研究新的量子技术，主要有三种情况：其一，1905年爱因斯坦提出“光量子假说”以说明“光电效应”。1916年，爱因斯坦指出辐射有自发辐射和受激辐射两种形式。受激辐射、粒子数反转概念和光子学中的干涉仪器件等形成了激光技术。其二，在薛定谔的多体波函数启示下，1926年狄拉克研究全同粒子系统。后在其他科学家的努力下，固体量子论得以提出，推动了1947年晶体管的发明。其三，量子力学中有一个著名的量子隧道效应，它是指微观粒子能够借助“隧道”越过势垒达到经典粒子不可能出现的区域，也能够不出现在经典粒子能够到达的区域。1981年，IBM公司苏黎士实验室的宾尼和罗雷尔利用电子的隧道效应制成了扫描隧道显微镜（STM），后来不断发展成为“扫描探针显微镜”家族，具有广泛的用途。这三种情形是通常意义上的量子理论对量子技术的直接或间接启示或某种程度的应用，它们并没有带来大规模的量子技术的广泛应用。

还有一种更重要的情形，就是直接建立在量子力学和量子信息理论基础之上的量子信息技术，将量子理论的研究与应用提升到一个新的水平。这成为第二次量子革命的标志。20世纪20年代形成的薛定谔波动方程等量子力学基本理论，则构成了第一次量子革命的主要内容，在技术上，主要是利用量子效应来制作新的量子器件。

前三种量子技术将量子纠缠（包括EPR关联）作为一个概念或作为一种有待确定的东西或佯谬来看待，而量子信息技术将量子纠缠作为一个基本的物理性质或科学事实来看待。量子纠缠从概念或佯谬到科学事实是量子信息技术的基本特征。

量子算法也取得了进展。魏斯纳（S. Wiesner）早在1969年就提出利用不确定性原理制造不可伪造的量子钞票的思想，后来这一想法受到本内特的重视。1982年，本内特与布拉萨德（C. Brassard）利用量子比特进行储存来实现量子公钥密码算法。1984年，布拉萨德与本内特提出了量子密钥分发的概念，构造了著名的BB84协议的密钥分发协议。BB84协议标志着量子密码学的真正开端。1994年，肖尔（Peter Shor）提出了肖尔量子算法。

到20世纪后半期，量子计算、量子密钥分配算法和量子纠错编码等3种基本思想的出现，标志着量子信息论基本形成。2000年，本内特等在《自然》杂志撰文指出，量子信息理论已开始将量子力学与经典信息结合起来，成为一门独立的学科。

自20世纪初到20世纪20年代建立量子力学后，发生了第一次量子革命，量子力学取得了巨大成功。这一时期的基本任务是建立量子力学的基本理论，检验量子力学是否正确和完备，基于量子效应的量子技术产品还较少。始于20世纪末的第二次量子革命，基于量子力学和量子信息理论，发展出新的量子技术，特别是量子信息技术，除此之外，这一时期的超弦理论研究、多体系统的量子纠缠的研究（如对拓扑物态的研究）等同样发挥了巨大作用，它们共同形成了第二次量子革命，将形成不同于经典计算的量子计算。

量子信息与量子计算紧密相关。在第一次量子革命中，信息并没有与量子力学发生多大的联系，所处理的信息是经典信息。在第二次量子革命中，量子信息理论产生了，所处理的信息是量子信息，量子信息成为理解和应用量子理论的重要基础。

经典信息就是我们日常见到的信息，它立基于经典物理学的物质性质与物理规律。经典信息用经典比特来衡量，一个经典比特就是一个0或1的状态，即要么是0，要么是1。一个经典比特就是一个两态系统，例如，一个状态的0或1，一个命题的真或假等。经典信息是经典计算的基础。经典计算的硬件是经典物理的物质性质，经典计算的软件是经典物理与数学的语言，这两者是相互适应和配合的。

量子信息不同于经典信息。量子信息建立在量子力学与量子信息理论的基础之上。一个量子系统包含大量的微观粒子，目前还不知道具体的微观粒子相互作用的机制，但是，幸运的是，我们能够用量子态来描述量子系统。量子态就是量子系统的状态。一个波函数（或概率幅）就是对量子态的完全描述。直接用量子态来表示信息，就是量子信息。用量子态来表示信息是量子信息理论的出发点，量子信息的演化遵从薛定谔波动方程，量子信息的处理就是量子态的幺正变换，量子信息的提取就是对量子系统实行量子测量。一句话，量子态就是量子信息，要从量子态角度来理解量子信息。当然，我们可以想象量子信息与量子态并不是一一对应的关系，但是，从操作层次上讲，我们界定量子信息就是量子态，由此展开量子计算与量子算法，原因在于已有量子算法都是从量子力学的规律来展开思考的。

量子信息的单元称为量子比特（qubit）。一个量子比特是一个独立的双态系统。两个独立的基本量子态，可以称为量子态与量子态。[4]经典信息0或1是不可以任意叠加的，而且0与1的叠加也不表示任何意义。比如，经典信息0+1=1就没有任何物理意义。对于量子信息来说，其独特之处在于量子信息满足量子力学的态叠加原理，可以是无限多个量子态的任意叠加，这都是有物理意义的。量子信息的叠加，将产生新的物理意义。牛津大学的多依奇（D. Deutsch）认为：“量子比特是一个物理体系，而不是纯粹抽象的概念，这是信息的量子理论与经典理论的又一重要区别。”[5]

量子信息的最基本单位是量子比特，一个量子比特是两态量子系统的任意叠加态。例如：

与经典信息不一样的是，经典信息不满足叠加原理，而量子信息满足叠加原理，而且两个独立的量子态与可以构成任意的量子信息，这两个独立的量子态称为基矢，就像通过x、y轴构成坐标系中的单位矢量一样，其中，a与b均为复数，經过量子测量得到经典信息0的概率是，得到经典信息1的概率是，这就是说，有一定的概率获得相应的经典信息，而且，即获得经典信息0与1的总概率为1。态叠加原理表明，量子信息如水波一样是可以叠加的，而不同于一个实物粒子在同一个时空点只能有一个粒子。量子信息又是不同于水波那样的经典波，量子信息显示的波是概率波，其振幅的绝对值只能是1，而水波振幅的大小具有物理意义。由与构成的一个量子比特的量子信息，只要a与b（它们都是概率幅）满足绝对值的平方之和等于1，那么，a与b就有无限多种选择，这就意味着1量子比特可以表达无限多个数据，而一个经典比特的经典信息，只能存储0或1一个数。

一个量子比特可以用一个单位球面来表示。一个经典比特只是0或1两个值，而一个量子比特有无限个值，分布在整个单位球面上。经典比特可以看成量子比特的特例（a=0或b=1）。一个经典比特如一个通常的开关，仅有开、关两个状态;而一个量子比特如一个球形的旋钮，这是一个上下、左右都可360度旋转的旋钮。量子比特的物理载体是任何两态的量子系统。量子系统就是微观的物质系统。比如光子、电子、原子、原子核等都可用来表示量子比特。

量子信息具有不同于经典信息的特点。一是量子不可克隆定理（no-cloning theorem）。最早在1982年，由伍特斯（Wootters）和朱雷克（Zurek）在《自然》杂志上提出了该定理。[6]量子克隆是指，原来的量子态不被改变，而在另一个系统中产生一个完全相同的量子态。量子力学证明，量子信息是不可克隆的。而经典信息可以完全克隆。需要注意的是，量子态的克隆不同于量子态的传输。在量子隐形传态过程中，一个未知量子态就能够从原来的量子系统中消失，而在另一个相距很远的量子系统中出现。

量子态不可克隆是量子密码术的重要前提，它确保了量子密码的安全性。在经典信息的窃取中，往往是复制经典信息而不让对手知道，如果知道信息被对手窃取了，那么，被窃者就会改变信息。对于量子信息来说，如果窃听者拦截了量子态（量子信息），那么，由于量子态不可复制，接收者原本应该收到的信息就收不到了，由此可以判断量子信息被拦截了，从而改变量子信息。

量子力学有一个不确定性原理，它是说我们不能同时准确测量坐标与动量等共轭量。如果量子信息（量子态）可以复制，那么，就存在许多完全相同的量子态，于是我们就能够同时在一个量子态中测量坐标，而在另一个量子态中测量动量，这就是说，我们能够同时准确测量坐标与动量，这就与不确定性原理相矛盾。

量子信息另一个重要特点是，它不可以完全删除，而经典信息可以完全删除。业已证明，任何未知的量子态的完全删除都是不可能的。[7]量子信息不可完全删除，意味着量子信息具有某种程度的物质性和客观性，这与物质不能被消灭有某种程度的相似性。但是，量子信息可以被创造，这点与经典信息一样，因为量子信息是用量子态来表示的，而量子态是量子系统的状态。

量子计算的基本特点

任何计算都由物理系统来实现。我们现在拥有的计算机是经典计算机，其原理与算法遵从经典物理学的规律。量子计算机既是一个量子力学系统，也是一个量子信息系统。量子计算是量子态的演化过程，是对量子信息的处理和操作。量子计算遵从量子力学、量子信息理论的原理，相应的量子算法不同于经典算法。目前，实现量子计算已不存在理论上不可跨越的障碍，但现实中实现量子计算还有一定的路程。2019年，谷歌研发的53个量子比特的量子计算机相对于超级经典计算机形成了巨大的优势。量子计算机之所以具有巨大的优势，在于它有显著的特点：

（1）量子存储器有巨大的存储能力。量子计算机的基本存储单元是量子比特。一个量子比特，系数a与b有无限多种组合，理论上一个量子比特可以存储无限个数。在具体操作中，一般令a=b，成為等幅的量子比特态，相当于1个量子比特可以同时存储两个数（0和1），即0与1都可以。

一个经典比特可以制备在两个逻辑态0或1中的一个态上，而不能同时存储0和1。一个量子比特可以制备在两个逻辑态0和1的相干叠加态上，即是说，它可以同时存储0和1两个状态。对于有n个量子比特的量子存储器，同一时刻将存储2n个数的叠加态，而在经典情况下，同一时刻只能存储2n个数中的一个数。可见，量子存储器具有巨大的存储能力。量子存储器描述了可存储的各种可能的、不同的态的同时存在，这是不同于经典存储器的显著特征。

（2）量子计算具有真正的并行性和整体性。要对量子信息进行处理，需要研究量子系统的演化，了解其演化有什么规律。由于量子信息就是量子态，即波函数，因此量子信息的演化必须满足薛定谔方程。为研究方便，假设量子系统的状态可以通过演化算符U来描述，量子算符相当于经典力学中的力。将U定义为，可以推论得到演化算符U满足方程，而且演化算符U具有幺正性，即UU+=U+U=1，所谓幺正性，就是指算符相当于单位量（或一个单位矩阵）。

可见，量子计算的一切逻辑操作必须是幺正演化;量子信息处理的逻辑操作是可逆的，因为幺正操作总有逆操作存在。幺正性是量子力学系统的核心。量子计算就是对编码的量子态进行一系列的幺正演化。对量子比特进行的简单幺正操作称为量子逻辑门。量子逻辑门将量子力学系统的一个态变换为另一个态。

量子计算的平行性由量子算法的并行性决定。量子力学中的所有运算是幺正变换和线性变换。

每1个量子算符U将1个初态变换为2个量子态的叠加，比如，;2个量子算符就将2个初态变换为4个量子态的叠加;3个量子算符就将2个初态变换为23=8个量子态的叠加，这三个量子算符U是同时作用的，这相当于3个量子算符U就是一次并行处理。n个量子算符对2个初态的一次操作得到2n个量子态的叠加。

量子计算机对n个量子存储器实行一次操作，即同时对所存储的2n个数据进行数学运算，等效于经典计算机重复实施2n次操作，或者等效于采用2n个不同的处理器进行并行操作。无疑，量子计算机可大大提高经典函数的运算速度。事实上，这里将量子计算与经典计算仅就2n个操作进行简单比较，是有严重问题的，因为经典计算的各个经典物理态不可能具有叠加、相干和纠缠等量子态所具有的性质，这才是量子计算所独有的优势。

量子计算的并行性也表现为一种整体计算，这是因为量子信息就是量子态，量子态存在于全空间中，并不定域于某个具体的区域，除非量子态被量子测量后转变为经典物理态。通过构造一个量子算法能够对一个量子信息的结构进行整体判断，而不必要知道细节信息。

所谓并行计算，就是计算机同时对所有数据进行计算。经典的并行计算是大量计算机的并行工作，但是各计算机分支之间并没有相干性或叠加性。量子计算的并行计算不同在于，量子计算的各个分支之间具有叠加性、相干性和纠缠性等新的特点。量子算法能处理整体性（全局性）问题，而经典计算只能处理局域性问题。

（3）有的量子算法具有加速能力。量子计算不仅其硬件是量子系统，而且其软件也是基于量子力学的规律或规则，即量子算法必须满足量子力学的规律。目前，科学家已提出一些著名的量子算法。

RSA公钥系统的安全性是基于数论的研究成果，经典计算机对大数进行因子分解是十分困难的。因子分解是指，已知一个n位整数N，去求两个未知的素数n1和n2。所谓素数，是指一个大于1的自然数，除了1和它自身之外，不能够被其他自然数整除。比如，2、3、5、7、11、13、17、19、23等就是素数。21=3×7，21就不是素数。素数被用在公钥系统的安全设计中。在信息编码过程中加入素数，编码之后的信息传送给收信人，只有收信人拥有密钥，才能有效地进行解码，获得传递的信息。因为任何人都可以收到编码之后的信息，如果没有密钥，你就必须解密，即找到另一个素数，但是因为寻找素数时间太久，而使得信息的破解就没有现实意义了。用计算机计算49×457=？，容易得到结果。但是，求一个数493的两个素数因子，即493=？×？，就非常困难，一个整数越大，因子分解就越困难。

经典计算机的因子分解的算法，是依次用2，3，…，作为除数去除N，直至把能整除N的那些素数找出来。采用这种算法，计算的时间复杂度为O（），这是一个指数复杂性的算法，不是一个有效的算法。如果正整数的位数n很大，即便是超级经典计算机也是无法在有效的时间内求解的。

1994年，AT&T公司的肖尔提出了肖尔量子算法，从而解决了正整数的因子分解问题。肖尔量子算法的因子分解思想，就是把求数N的因子问题简化成求一个周期函数f的周期问题，然后利用傅立叶变换找出函数的周期。设输入量子寄存器的量子位数为n，通过量子傅立叶变换（Quantum Fourier Transform），肖尔证明，基于2n的量子傅立叶仅用n（n+1）/2个量子门就可实现。就是说，量子傅立叶变换所需要进行的运算与位数是多项式关系，即肖尔量子算法是一个多项式算法，这是一个有效算法。算法复杂性理论表明，指数复杂性是真正复杂的，而多项式复杂是实际上可求解的。

肖尔量子算法利用了量子态的相干性、量子纠缠等性质，这是经典算法所不具有的性质。比如，对十进制60位的数进行因子分解，如果用运算速度约为1012次/秒的经典巨型计算机进行计算，运算次数约1030次，耗时1017秒，大约相当于宇宙的寿命（约为1017秒）;但是，采用肖尔量子算法条件下，需要作的运算次数约为40，000次，以同样的运算速度，只需要10-8秒即可完成。如果量子计算机实现了，那么非常容易破解RSA公钥系统的密码。目前一个推广的肖尔量子算法在核磁共振中得到实验检验。

1997年，格罗夫（Grover）发现了量子搜寻算法。所谓搜寻算法，就是从N个未分类的客体中寻找出某个已知的客体。经典算法只能是一个接一个搜寻，统计而言，这种算法需要寻找N/2次，找到的概率为1/2，但是，用格罗夫量子搜寻算法仅需要次。例如，要从100万个电话号码中寻找出特定的号码，经典算法需要N/2=50万次，其正确的几率为1/2，格罗夫量子搜寻算法只需要=1000次，其正确答案的几率为1/2，但若再多重复操作几次，那么找到所需电话号码的几率接近于1。[8]

2009年，美国麻省理工学院罗伊德（Seth Lloyd）等，利用量子计算的并行性，提出了用于求解线性方程组的量子算法，认为该量子算法可带来指数级的加速，将远超现有经典计算机的速度。[9]据理论估计，求解一个亿亿亿级变量的线性方程组，利用GHz时钟频率的量子计算机将只需要10秒钟的计算时间。利用多光子纠缠操控技术，中国科技大学潘建伟教授等从实验上运行了求解一个2×2线性方程组的量子线路，首次从原理上证明了这一算法的可行性。[10]

可见，目前已创造出来的一些量子算法已显示出强大能力，能够克服某种经典复杂性。有的问题是指数加速（如肖尔算法），而有的問题是方根加速（如格罗夫算法），也有一些问题（如迭代问题、宇称问题等）没有量子算法的加速。量子算法之所以有显著优于经典计算的能力，在于量子算法充分利用了量子态（量子信息）的叠加性、相干性、非定域性和纠缠性等量子特性，它是用量子力学的语言编写出来的程序。

量子纠缠、量子信息与量子实在

为了认识量子信息，需要认识一个非常重要的量子隐形传态（quantum teleportation），其基本过程见附录。为实现量子态的隐形传态，其关键步骤如下：

（1）制备量子纠缠源（比如，有一对微观粒子构成量子纠缠态，分别由张三与李四各拥有微观粒子2与粒子3），该纠缠态构成了量子信道。

（2）对需要传递的未知粒子（如未知粒子1，）与量子纠缠源中的发送者（张三）拥有的粒子（如粒子2）实现联合贝尔基测量，即一种纠缠态测量。实际上，这实现了本体论量子信息（未知粒子1的概率幅a和b）的传递。

（3）将纠缠态（如粒子1与粒子2）的测量结果（处于何种量子纠缠态）通过经典信道（如打电话）传递给接收方。

（4）接收方（李四）将收到的经典信息与量子通道的信息结合，对纠缠源中接收者拥有的粒子实行相应的量子变换（一种幺正变换，即一个矩阵），从而恢复到未知粒子的量子状态（如粒子3的状态为：）。

必须指出的是，一旦张三对粒子1与粒子2进行贝尔量子纠缠态测量，那么，未知粒子1的概率幅（即系数）a和b，就立即、马上传递给（类空间隔）很远的李四，这里的概率幅a和b就是量子信息，是处于本体论状态的量子信息（称为本体论量子信息），即它存在着，但人们并不知道量子信息具体处于何种状态。但是，当张三将粒子1与粒子2所处的具体的贝尔态通过经典信道告诉李四，那么，李四根据得到的经典信息做出相应的幺正变换，就能够恢复出未知粒子1的准确状态，此时的量子信息就转变为认识论状态的量子信息（即认识论量子信息），获得的认识论量子信息不违背狭义相对论原理，信息传递不超过光速。

无疑，量子纠缠态是隐形传态的根本所在。量子纠缠（quantum entanglement），远比缠绕的线绳要复杂得多，是一个难以理解的量子物理现象。在量子力学中，“纠缠”这一名词的出现可以追溯到量子力学诞生之初。纠缠（entanglement）的概念最早来自于薛定谔于1935年发表的薛定谔猫态的论文，猫的死态、活态与放射源放出一个粒子或没有放出一个粒子相纠缠。[11]爱因斯坦等人于1935年提出的EPR论证中已包涵了量子纠缠的想法。设想由两个子系统F和G构成的复合系统，若其量子态不能表示为子系统态的直积，则称为纠缠态，即复合系统的波函数（几率幅）不能表示为子系统的量子态的直积：。

日常生活中，有许多关于量子纠缠的比喻。比如，有人说，有一对母女，设女儿处于广州，而母亲处在旧金山，当女儿生了小孩，那么，远在旧金山的母亲就立即成为外婆，这里不需要有任何信息的传递。显然，处于广州的女儿与处在旧金山的母亲之间并不能进行瞬间的量子信息的传递。日常生活中的这些量子纠缠的比喻，都是错的。量子纠缠是一个纯粹量子现象，不是经典现象所能够比喻的。在量子隐形传态过程中，量子纠缠成为传递量子信息的通道，而任何经典的类比，都无法实质性地瞬间传递信息。

但我们可以用数学来理解量子纠缠。设两个微观粒子F与G构成一个复合量子系统S，如两个光子构成一个复合系统。设粒子F有两个状态（即量子态）和，就是说，在同一时刻，这两个状态不可能同时存在，依据量子力学的态叠加原理，粒子F的状态可以写为：，它表示粒子F处于态，或者处于态;粒子G也有两个状态和，可大致写为：。

如果复合系统的状态为，那么，我们可以将该状态分解为和的“乘积”，即可以把作为公因子提出来，，这相当于系统F处于态，而系统G处于态，系统F与系统G还没有发生纠缠，态就称为可分离态，就不是纠缠态。又如，也是一个可分离态。

对于状态为，能否有适当的系数a、b、c与d，使得？显然，不存在那样的系数a、b、c与d。态，就称为纠缠态。纠缠态仅存在于量子系统中，纠缠只能是量子纠缠。从数学的因式分解来看，不能把一个复合态分为两个分离态的“乘积”，复合态就是一个纠缠态。或者说，不能进行因式分解的，就是纠缠态;能够进行因式分解的，就不是纠缠态。量子纠缠是微观物质的根本性质，它以非定域方式存在。量子纠缠是量子多体系统所特有的现象，它是多体量子叠加态。多体之间存在的量子纠缠超越了时空限制，以非定域方式存在。

在量子隐形传态过程中，未知量子态从张三那里消失，并经过一个延迟时间（经典通信时间与李四操作所需要的时间）出现在李四那里。这正如李承祖教授等学者所说的：“这有点像‘借尸还魂，原来的张三拥有的那个未知态的‘魂，在李四的那个量子位上‘复活了。”[12]这里所谓的“魂”实际是指未知态的系数（概率幅）a与b。这有点像道教八仙中的铁拐李，原来的铁拐李十分英俊，他将元神投入到饿殍上，就成为后来又黑又拐的神仙铁拐李了。

在量子态的传送过程中，原来的未知粒子1的状态已被破坏（粒子1与粒子2发生了量子纠缠），粒子3不是粒子1的复制，而是粒子1的传递，这正是量子不可克隆定理的一种表现。

2011年，由中国科学技术大学牵头提出并策划的中国科学院战略性先导科技专项“量子科学实验卫星”获得立项。2016年8月16日，中国成功发射了世界第一颗量子科学实验卫星“墨子号”，用于探索卫星平台量子通信的可行性。该量子卫星装备了量子密钥通信机、量子纠缠发射机、量子纠缠源等设备，是世界上第一个太空中的量子通信终端。地面配备了北京兴隆、云南丽江、乌鲁木齐南山、青海德令哈四个地面站用于星地量子密钥分发和星地量子纠缠分发实验，并配备了西藏阿里地面站用于地星量子远程传态实验。[13]这是中国量子实验卫星星地空间的量子隐形传态的过程。

从更一般的角度来看，按照大爆炸宇宙学，宇宙的演化是从量子宇宙演化为经典宇宙，于是，在人类存在以前，这个信息就存在和演化着，这个信息就是本体论信息，既有本体论量子信息，也有本体论经典信息，它反映了宇宙的客观信息。只有当人们用有关理论去分析宇宙的本体论量子信息时，它才转变为认识论量子信息。所謂本体论量子信息，是指微观事物的量子状态与关联方式的自我显现。所谓认识论量子信息，是指微观事物的量子状态与关联方式对主体的显现。[14]定义的“关联方式”包括叠加性、相干性与量子纠缠等性质，量子信息的本质是通过量子态、量子相干和量子纠缠等量子性质展现出来的。

认识论量子信息意味着人们能够认识和把握它，而本体论量子信息，是指它本身存在着，人们还没有认识它，或者对它的认识不完全或不确定。可见，本体论量子信息与认识论量子信息的划分具有相对性。我们说量子信息分为本体论量子信息与认识论量子信息，但实际上两者是统一在一起的，这种分类只是它们在不同视域中的显现。从认识论来看，本体论量子信息不等于不可知，而是部分可知，或者说，本体论量子信息原则上是可知的。否则，如果本体论量子信息是绝对不可知的，那么，就是不可知论了。认识论量子信息，是更可为人们所知，也不是绝对可知。如《论语·为政》中记载的，孔子曾说：“知之为知之，不知为不知，是知也。”这说明，知包含了知与不知两个方面，知是知与不知的统一。

在量子隐形传态过程中，本体论量子信息的传递是超光速的，而认识论量子信息的传递是不快于光速的。

我们能不能把量子信息看作微观物质的普遍属性？电子、质子等微观粒子的性质都可以用几率幅（波函数）加以很好的描述。我们认为，量子信息可以看作微观物质的属性。量子信息的产生要以微观物质的运动为前提。任何微观物质的量子运动都会有量子信息产生。量子信息只能存在于量子系统之中。这是因为量子信息产生的物理基础是处于量子系统中的微观物质或微观事物。信息是物质自身的某种显现或某一方面、侧面或层次性质的显现。在黑洞的无毛定理中，“三根毛”就是黑洞本身的某种显现或某个方面或侧面的显现。

用量子态来表示信息是研究量子信息的出发点。量子态本身是一种状态，是物质的一种状态，这种状态又显现为另一种东西——量子信息。就如一个人有一个物理实在，但它又可显现为人的高度、重量等信息，两者是二而一的事情。量子信息不是量子实在，而是作为量子实在的状态、关联、变化、差异的表现。

列宁认为：“物质是标志客观实在的哲学范畴，这种客观实在是人通过感觉感知的，它不依赖于我们的感觉而存在，为我们的感觉所复写、摄影、反映。”[15]可见，“客观实在”与感觉的“复写、摄影、反映”构成了物质相互依存的两个方面。客观实在反映了物质的自我同一性，反映的是物质的肯定的方面，即物质之所是，不在于展示，反映的就是“物质就是存在”，没有必要向他者传递自身是什么，但可以自我显现，这是一种原初的存在，是一种自在，也是一种“无”，它无欲无求，本身是自足的。正是“物质”的这种否定性的“无”使得物质自身能够运动变化，以至于能够向他者传递信息。感觉的“复写、摄影、反映”实质上是物质向他者传递信息，让他者知道物质之所是和何所是，这就使得物质具有诠释的可能性，物质的这一性质实质上揭示了信息的特性，即物质的信息特性，它反映的是物质与他者之间的关系与关联方式。“复写、摄影、反映”不是主体对物质的任意阐释，而是主体对物质的真实诠释，即物质是因果之源，主体对物质的诠释必须是因果的、规律的、有理由的，在多种可能的选择阐释中需要进行权衡等，这从一个角度启发了物质诠释学。

在这一意义上，物质当然不等于信息。信息就是物质的状态与关联方式的自我显现，关键在于向他者传递、显明或解蔽物质之所是。可见，物质的客观实在性与信息是相互统一的。信息不是物质，但是，信息与物质又是相互联系的。本体论信息显现着物质的存在方式和状态，信息与物质是统一的。正如夏立容所说：“信息是以物质为载体并与物质一起规定着客观事物的功能及特性。因此，可以说本体信息与物质同在。”[16]我们的自然界既是一个物质世界，又是一个信息世界，即世界是物质与信息的统一。

对于微观物质而言，量子实在就是微观物质自身同一性的显现。量子信息就是微观物质的状态与关联方式的自我显现。这里的“显现”还有一个在什么境域中显现，通过什么来显现，以及向谁显现的问题。量子实在与量子信息是微观物质的两个统一的方面，共同揭示了微观物质何所是、之所是与如何是。微观物质自身与微观物质的状态和关联方式（如量子态）是不相同的，这就是说，量子实在不同于量子信息。量子信息不可复制与不可完全删除，说明了量子信息具有某种程度的实在性，可称为半量子实在（half quantum reality）。

世界的复杂性是主观与客观的统一

世界是复杂的，复杂性表现为许多方面。从计算入手，将有利于认识世界的复杂性。计算是一个物理的运行过程，完成这一过程需要基本的运行时间和运行空间。计算按程序进行，程序是由算法与数据构成的。同样的问题，可以有不同的算法。针对实际问题需要选择一个好的算法，这样才能构造出一个效率高的程序。算法就是求解一类问题的方法，或者是某种指令集。

计算的复杂性用算法复杂性来衡量。计算复杂性是由算法的复杂性决定的。计算复杂性分为时间复杂性和空间复杂性。时间和空间是计算最基本的物理限制因素，计算时间与空间都是有限的，且与人类活动的合理的时间与空间尺度密切相关。运行一个算法所需要的时间和空间越多，说明该算法的复杂性越高;反之，说明该算法的复杂性越低。如果一个算法超出了一个合理时空尺度，计算就是不现实的。

计算复杂性是算法所求解问题规模的某个函数。一个问题的规模，一般用自然数n来度量它的大小。对函数来说，n可能是自变量的个数;对矩阵来说，n可能是元素的个数等。一个问题的复杂性是该问题规模大小n的函数。算法的复杂性讨论中，最为重要的是渐近复杂性。问题规模n越大，计算越复杂。

不同的算法有不同的时间复杂性。研究表明，对于多项式时间复杂性函数，工作量随问题规模n增长而增长的速度都比较平缓，但对于指数时间复杂性函数，这种增长到后来就非常剧烈。[17]简言之，指数复杂性难以克服，而多项式复杂性是可以克服的。而且计算机速度的提高，也不能有效克服指数复杂性。提高计算机的速度，对计算机的指数复杂性处理改善较小。计算机科学和计算数学把多项式时间算法看作“好的”算法，把指数时间算法看作“不好的”算法。

计算的复杂性涉及递归函数等。所谓原始递归函数，是指从初始函数出发，经过有限次的代入与原始递归表达式而做出的函数。1934年，哥德尔提出了一般递归函数概念，它是指从初始函数出发，经过有穷次使用代入、原始递归表达式和μ算子而做出的函数。后来，丘奇（A. Church）等人证明一类可计算的函数（即λ可定义函数）就是一般递归函数。丘奇发表著名的丘奇论题：每个能行地（有效地）可计算的函数都是一般递归的。可计算函数涉及一个图灵机模型。将程序和数据以数码的形式存储于带子上，这就是“通用图灵机”原理。1936年，图灵（Alan Mathison Turing）定义了另一类可计算函数，即图灵可计算函数。图灵证明了图灵可计算函数与λ可定义函数是等价的。丘奇论题和图灵论题实质上谈论的是同一回事，统称为丘奇–图灵（Church-Turing）论题：任何能行的（有效的）可计算函数等同于通用图灵机可计算的函数。

1985年，多伊奇（D. Deutsch）将各种物理系统的演化看作真实世界中一直存在着的计算过程，他提出了丘奇–图灵论题的“物理版本”：“每个有限可实现的物理系统都能由一个通用模型计算机以有限方式的操作来完美地模拟。”[18]在这里，多伊奇强调了自然计算受到物理定律的限制，但是，我们也并不能完全否定计算的逻辑和数学本质。

不仅时间与空间的现实合理尺度构成了计算复杂性，而且丘奇–图灵论题揭示了哪些问题是可计算的，哪些问题是不可计算的，即存在不可计算问题。不可计算问题的存在，意味着世界本身是复杂的。目前有关计算复杂性的定义是操作性和现象性的，并没有揭示计算复杂性的本质。已有的计算复杂性理论属于经典计算理论，复杂程度与算法有关，只有多项式时间算法是可计算的，而指数时间算法是不可能克服其复杂性的。

量子计算理论表明，某些经典的指数时间算法可以转化为量子多项式时间算法，即经典时间复杂性可以克服，比如，肖尔算法就是这样的量子算法。已发现格罗夫算法等可以比经典算法更快地求解问题。经典复杂性和量子复杂性都属于数学的复杂性，这里的问题是，数学的复杂性就是先天的（a priori）、固有的、客观的，是不可改变的吗？

一般认为，数学世界是一个具有高度自主性的世界，也是一个客观世界。原来的计算问题没有经典算法解，现在却有量子算法解，这意味着数学世界并不是一个固定不变的、绝对的世界，而是一个可能世界。说数学是一个可能世界，是指数学是合乎逻辑的，是逻辑一致的;数学世界有多种可能，即只要符合逻辑，就是数学的真理。有的经典计算的指数复杂性，是一个认识复杂性问题，而不是客观复杂性问题，其解取决于人的认识能力和人创造的工具的水平。

一般来说，“客观的”意味着事物本来的面目，与人的意识无关，不是人想怎样就怎样，不以人的意志为转移。对于经典物理世界来说，“客观的”还意味着事物本身的内在性质是不变的，或者说，事物是固有的，有固定不变的内在性质，比如，事物的规律是不变的。对于数学世界来说，“客观的”意味着符合逻辑与人的意识无关。“客观的”不同于“认识的”。

这里会产生这样一个问题：有没有离开认识条件（如实践手段等）的客观对象？如果客观对象是固定的、不变的、刚硬的，那么，人们就无法通过技术等实践手段作用于该客观对象，人们也就无法认识客观对象，因为客观对象在各种技术等实践手段的作用下都没有任何变化，客观对象就是不可知的。如果客观对象自身在变化，那么，人们就可以通过观测仪器等实践手段去观察它。

研究世界的复杂性，有一个追问的方式或视角的问题，你是从数学来追问，还是从计算机科学来追问，这是有区别的，因为数学与计算机科学不一样，前者是可能世界，而后者是建基于数学的物理世界。

在康德的先验哲学中，先天的（a priori）知识并不表示该概念或范畴是人生下来就具有的，而是说，先天知识是验前知识，即进行一项实验或观测之前人们所具有的知识，具有一定的普遍性和客觀性。从这一意义上讲，数学世界也是一个先天的世界，数学所具有的复杂性是一种先天复杂性。但是，本文认为，更准确地说，这是超验（trans-empirical）复杂性。所谓“超验”，是指超过经验，又不离开经验，还使经验得以可能。[19]这种超验复杂性将会随着自然科学和技术的发展而改变。

数学构成的是一个可能世界。当物质性经验因素与数学的可能世界相联接，那么，数学的可能世界就转变为一个现实的经验世界，或现实世界。比如，对于1、2、3……等自然数，显然它们具有经验内容，由这些自然数构成的世界就是一个经验世界。但是，当自然数从有限趋向无限时，数就从现实走向可能世界，或者说，自然数的经验世界与可能世界是联接在一起的，并不一定有一个绝对的区分。计算机世界是一个数学与物理相结合的世界，即可能世界与现实世界相叠加，成为一个可能的现实世界，或现实的可能世界，这意味着计算机世界既是现实的，又是可能的，从而为人的创造性留下了巨大的空间。

我们可以这样看，世界是客观实在的，是不以人的意志为转移的，但是，这个“客观实在是什么”，却依赖于人们的理论和实践的认识，或者依赖认识条件。就是说，客观世界是实在的，但是，当人们言说客观世界时，就已经渗透了理论或语言，或者说是认识条件。这里的认识条件包括科学理论和技术水平。言说客观世界，总是与理论和技术有关的。按照上述观点，世界的复杂性是客观的，但是，其客观的复杂性如何表现则取决于主体的科学（含数学）理论和技术水平。

在经典物理或经典计算看来，计算是一个经典物理过程，经典计算需要一定的时间或空间，但在量子力学或量子计算看来，经典时间或经典空间并不具有量子意义，其需要的量子时间或量子空间可能变得很小，这取决于在量子计算过程中所进行的是何种性质的量子物理过程。

定性地讲，原来经典意义上的较大的时间和空间，都可以由于量子力学的不确定关系，在不同性质的量子测量条件下，在微观粒子的运动面前变得非常小。这是由于时间或空间的不确定，使得量子信息可能很快（甚至超光速地）穿越经典的空间。

经典时间和经典空间、量子时间和量子空间都是感性的时间和感性的空间，它们都是物质存在（being）的形式。物质是实践的物质。时空就是实践的物质的存在形式，其实质就是，时间空间是物质实践的时间空间，并没有离开（技术）实践的时间空间。实际上，狭义相对论表明，运动的杆缩短与运动的时钟变慢，都揭示出测量者所在坐标系会直接影响时间与空间的大小。牛顿所谓的绝对时间与绝对空间是不现实的，也是没有的。时间和空间都具有客观性，但是，它们在不同的技术条件下将会有不同的显示。

哲学与发展量子科技的关系

2019年10月，谷歌在《自然》杂志发布信息称，其研发的可编程的超导量子计算机“悬铃木”（Sycamore）可对53个量子比特进行运算控制，在53个量子比特上创建量子态，对应于一个253维（约1016）的计算状态空间。该量子计算机对目前经典计算机形成绝对优势。[20]悬铃木可在200秒内对一个53量子比特的超导电路系统采样100万次，而当时世界超算冠军Summit则需要花费1万年。据此，谷歌认为量子计算实现了量子霸权（Quantum Supremacy）。在谷歌的量子霸权中，每个量子比特由超导器件来实现。“量子霸权”是加州理工学院理论物理教授普雷斯基尔（John Preskill）于2011年10月在布鲁塞尔举行的第25届索尔维物理学会议上提出的概念。他说，终有一天，量子计算机将远远超越经典计算机。[21]

2020年11月，中国科学技术大学潘建伟等与德国、意大利等国家的研究者合作，在超冷原子量子计算和模拟研究中取得重要突破：他们开发了一种量子计算机——71格点的光晶格量子模拟器，成功实现了对量子电动力学的施温格模型（Schwinger Model）的模拟，首次使用微观量子调控手段在量子多体系统中验证了描述电荷与电场关系的高斯定律。[22]

中国科学技术大学的研究也显示出量子计算具有经典计算所没有的计算能力，显示了量子优势。玻色子取样是经典计算机难以处理的任务。2020年12月3日，中国科学技术大学潘建伟等学者在《科学》杂志发文，成功构造出76个光子100个模式的高斯玻色取样量子计算原型机“九章”。利用热状态、可分辨光子和均匀分布等合理假设，检验了获得的样品，其输出状态空间维数为1030，采样速率比使用最先进的模拟策略和超级计算机快约1014次。[23]“九章”等效地比谷歌2019年发布的量子计算机“悬铃木”快一百亿倍，使我国成为全球第二个实现“量子优越性”的国家。

量子计算也显示出巨大成就，但是，仍然存在许多问题，主要表现为两个方面。其一是如何理解量子科学，因为有多种量子力学诠释，除了科学的理解之外，还需要从哲学角度来诠释量子力学;其二是量子信息技术已走在量子科学的前面，能否从量子信息的角度来统一量子科学与量子技术，需要有新的哲学概念来统摄并构造相应的量子科学理论，来统一理解量子力学诠释和量子信息理论。

量子力学有这么多诠释，其根源在于：第一，形式化。在量子力学的创立过程中，总是先有形式体系（即概念与规律），但是，该形式体系究竟表达的是什么意义，其中的物理量的涵义并不清楚，形式体系超前于其解释与说明。第二，观察者的作用并不清楚。观察者在不同的量子力学诠释中有不同的作用。在哥本哈根诠释、多心诠释和自洽历史诠释中，观察者发挥了重要作用。哥本哈根诠释认为，波函数的描述代表一个观察者对量子系统所能知道的全部知识。系综诠释、隐变量诠释、多世界诠释等认为观察者并不在量子测量中发生作用。第三，概率的涵义不清楚。在量子世界中，描述其波性质的是概率幅（波函数），概率幅的叠加就是波的叠加，这里的波是量子性质的波。概率幅（波函数）的绝对值的平方就是经典概率。这里的经典概率是倾向性的频率，还是主观的？理论的形式主义、观察者概念、理论的几率特点，这三个理由正是昂尼斯（Omnes）所提出的观点。[24]

笔者认为，还有以下两个原因导致需要量子力学诠释。第一，波函數（几率幅）的意义不清楚。薛定谔在波动方程的创立之初，通过与哈密顿–雅可比方程联系，将母函数S与未知函数相联系，并假设，当时未知函数的含义并不清楚，后来才取名为波函数。他将称为“力学场标量”[25]，还提出了波函数的电磁诠释。显然，这些创见都是探索性的。波函数究竟是一个工具式的数学描述，还是对量子世界的实在描述？正如中科院院士孙昌璞所认为的，对于量子力学诠释——理解波函数如何刻画微观世界，人们迄今为止并未形成共识。[26]笔者赞同波函数是相对结构实在的。[27]第二，量子世界本身的不确定性。一是由不确定原理所揭示的量子世界本身具有不确定性，于是有量子对象的不确定，因而在不同的技术条件下，将会产生不同性质的宏观量子现象，而宏观与量子之间并不是一一对应的关系。二是量子世界仅有一个，还是多个？不同量子力学诠释有不同的观点。多世界诠释认为，一个波函数，多个世界。因而，需要多种概念与理论体系来把握不确定的量子世界。

与经典的牛顿力学相比，作为常规科学的量子力学的概念与规律存在很大的争论，有不同的诠释框架，各种框架都有自己的理由，虽然有的科学家宣称自己的量子力学诠释更好一些，但别的科学家并不认同。一个概念在不同的量子力学诠释中，其含义也可能不同。事实上，每一种量子力学诠释都有自己的优点与不足，各有其存在的理由。在笔者看来，多个量子力学诠释的存在并不断发展，表明理解量子力学诠释的客观意义与延展意义是一个非常重要的问题，这揭示了量子力学本身内在是诠释学的。这就意味着，理解量子力学，需要从诠释学角度来展开必要的分析。[28]

不同的量子力学诠释有不同的概念与基本假设先行。之所以有不同的先行概念与假设，在于各种量子力学诠释的提出者有不同的哲学观念与对量子世界的预设。因此，提高哲学素质，是创造量子力学新范式的必要前提。

事实上，1935年爱因斯坦、波多尔斯基（Podorsky）和罗森（Rosen）（简称EPR）共同在《物理评论》发表的《能认为量子力学对物理实在的描述是完备的吗？》一文，在一定哲学前提下，利用理想实验的逻辑论证方式，论证了这样的结论：“波动函数所提供的关于物理实在的量子力学描述是不完备的（complete）。”[29]这里要强调的是，EPR说量子力学描述不完备，是指波函数针对物理实在，而不能忽视了物理实在，就是说，波函数关于物理实在的描述是不完备的。在这篇重要论文中，爱因斯坦等认为，任何描述物理实在的完备物理理论都必须满足两个条件：（1）完备性判据。“物理实在的每一元素都必须在这物理理论中有它的对应。我们把这叫做完备性的条件。”这是关于完备理论的必要（necessary）条件。（2）实在性判据。“要是对于一个体系没有任何干扰，我们能够确定地预测（即几率等于1）一个物理量的值，那么对应于这一物理量，必定存在着一个物理实在的元素。”[30]这是关于物理实在的充分（sufficient）条件，这就是说，物理实在的元素并不是由先验的哲学思考来决定的，而必须由实验（即经验）来度量。显然，它们都是哲学的分析。EPR论文被认为是EPR佯谬，原因在于当时量子纠缠尚未为人们所认识，直到1993年本内特等提出了量子信息理论，1997年该理论被实验检验，EPR佯谬才被视为科学事实，而且成为量子信息理论的先驱。

发展量子科技，必须加强相关学科和课程体系的建设。正如习近平总书记所指出的：“建立适应量子科技发展的专门培养计划，打造体系化、高层次量子科技人才培养平台。要围绕量子科技前沿方向，加强相关学科和课程体系建设，……发现一批创新思维活跃、敢闯‘无人区的青年才俊和顶尖人才。”[31]其中，要着重加强哲学研究和课程体系建设。正如爱因斯坦所说：“科学并不就是一些定律的汇集，也不是许多各不相关事实的目录，它是人类头脑用其自由发明出来的观念和概念所作的创造。”[32]“如果把哲学理解为最普通和最广泛的形式中对知识的追求，那么显然，哲学就可以被认为是全部科學研究之母。”[33]没有高水平的哲学学习和研究，就不可能有观念和概念的自由创造，也不可能原始地提出量子科学和量子技术理论，更不可能开创量子科学新范式和关键量子技术新范式。哲学有许多定义，并没有形成共识，但在笔者看来，哲学的如下定义是有启发意义的，即哲学就是概念的创造、推理和系统化的学问。[34]

目前，中国科学技术大学、中国科学院、清华大学等单位在量子科技的某些方面居于世界前沿。中国科学技术大学正在建设科学哲学系，由国际著名量子信息专家潘建伟院士担任系主任。独立的哲学教学与研究机构的重要性受到了我国“双一流”大学的高度重视，如华中科技大学于2020年将哲学系从人文学院独立出来，并成立了哲学学院，该院在康德哲学、科技伦理学等方面颇具特色。一方面，我国的一些大学在加强科技哲学的研究，这将有助于发掘量子科技的哲学意义，促进量子科技发展。但另一方面，由于学科与课时的调整，目前我国一些大学的科技哲学（自然辩证法）课程受重视程度有所减弱，这类情形将不利于我国大力发展科技哲学进而促进量子科技进步。

综上，要在自主创新、掌握和创造量子科技等关键核心技术上引领世界，除了相应的制度建设以及实施基础科学研究、基础技术研究之外，还要建立与前沿科技相适应的文史哲学科体系和课程体系，特别是要建立世界一流的哲学课程体系，培养学生的理性精神、怀疑精神和创新思维能力，加强哲学与前沿科技的联盟，促进科学家、技术家与哲学家就哲学与科技共同关注的问题展开多种形式的讨论和研究，激扬火花，创新可成。

附：量子隐形传态的基本过程

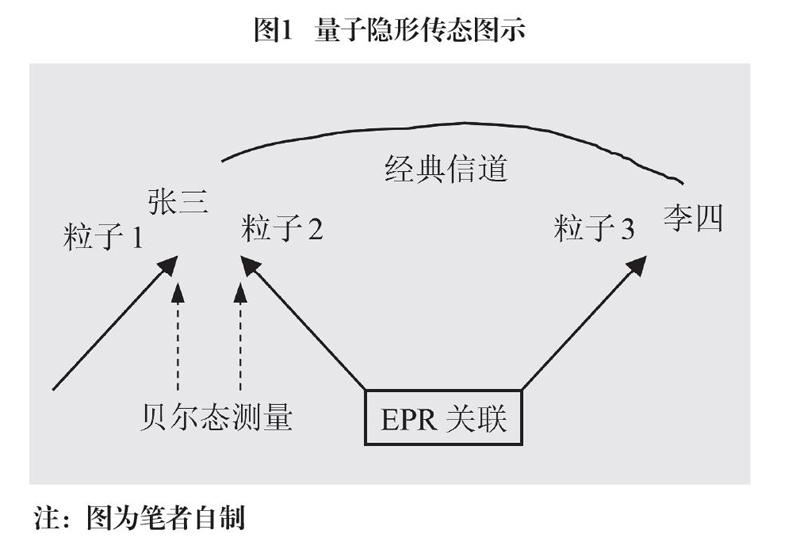
量子隐形传态显示了如何通过量子纠缠传递量子信息的过程。如图1所示。

假设张三要给李四传输一个未知的量子态（即微观粒子1），这就是未知的量子信息，它可以表达为：

其中a与b为未知复系数，满足，脚标1表示微观粒子1（下面2与3表示粒子2与粒子3）。就是粒子1的列矩阵。

为了传送未知量子态，还需要有另外两个粒子：微观粒子2与粒子3，且它们是量子纠缠的，并设粒子2和粒子3的纠缠关联状态（EPR关联就是一种纠缠态）为[35]，

其中，粒子2与粒子3处于量子纠缠态，它们并不具有独立性质，而是相互依赖地整体存在。即一个子系统的存在，依赖于另一个子系统。一旦对其中一个子系统的某个力学量进行测量，就能立即获得（与它相纠缠的）另一个子系统的力学量的值，不论它们相距多远。

为了将未知粒子1传送给李四，张三与李四必须分别持有粒子2与粒子3。张三还需要联合测量粒子1与粒子2，以获得经典信息，通过经典信道将测得的经典信息传递给李四，以便让李四采取相应的幺正变换，将李四得到的未知量子态粒子3变换为与原来粒子1同样的状态。

粒子1和粒子2构成的量子系统可以用著名的量子纠缠态贝尔态（Bell态）来表示。贝尔态是具有最大纠缠的量子态。在具体实验中，用识别贝尔态的测量装置对粒子1与粒子2进行联合测量（即贝尔态测量BSM： Bell-State Measurement）。这4个贝尔态表达为、、与。[36]3个粒子构成的复合系统的量子态可以用4个贝尔态来表示：

上式中，右边第一项中，表示微观粒子3的状态，其余作类似的理解。从该式发现，当张三对粒子1与粒子2进行一次联合测量，其结果是联合状态处于4个贝尔态、、与中的一个，概率相同（都为（1/2）2=1/4），而李四测得的粒子3则将是相关联的量子态，即分别是、、或描述的4个状态之一。[37]

比如，当张三测量得到的结果是，即粒子1与粒子2处于纠缠态，则粒子3必然处于，这时张三通过经典信道（如打电话、发邮件等）告诉李四自己测量得到的结果是，那么，李四就可以用获得的状态进行一个量子力学所特有的幺正变换，将之转变为与未知粒子1“相同”的量子态，即是说，原来的未知粒子1已经在粒子3处得到恢复了。其他情况类似。

可见，只要张三通过经典通信的手段告诉李四其在测量中得到的结果，李四就可以通过适当的操作恢复出未知粒子的状态，因为粒子3所处的4个状态都反映了未知状态的概率幅（即系数）a和b。

（本文系2019年国家社科基金重大项目“当代量子诠释学研究”的阶段性研究成果，项目编号：19ZDA038）

注释

[1][31]《习近平在中央政治局第二十四次集体学习时强调：深刻认识推进量子科技发展重大意义 加强量子科技发展战略谋划和系统布局》，《人民日报》，2020年10月18日，第1版。

[2]本文中的EPR是爱因斯坦（Einsein）、波多尔斯基（Podorsky）和罗森（Rosen）的简称。EPR关联是一种量子纠缠。EPR通道就是由EPR关联建立的量子联系。

[3]Bouwmeester， D. et al.， "Experimental Quantum Teleportation"， Nature， 1997， 390， pp. 575-579.

[4]严格讲，狄拉克符号标记两个独立的量子态：|0>和|1>。量子态用函数来表示，而且是复数。

[5][英]多依奇：《它来自量子比特》，载[美]约翰·巴罗等编：《宇宙极问——量子、信息和宇宙》，朱芸慧等译，长沙：湖南科学技术出版社，2009年，第51页。

[6]Wootters， W. K. and Zurek， W. H.， "A single quantum cannot be cloned"， Nature， 1982， 299， pp. 802-803.

[7]Pati， A. K.， et al.， "Impossibility of Deleting an Unknown Quantum State"， Nature， 2000， 404， p. 164.

[8]Bouwmeester， D.; Ekert， A. and Zeilinger A.， The Physics of Quantum Information， Berlin： Springer-Verlag. 2000， p. 413.

[9]Harrow， A. W.; Hassidim， A. and Lloyd， S.， "Experimental Quantum Computing to Solve Systems of Linear Equations"， Phys. Rev. Lett.， 2013， 110， p. 230502.

[10]Cai， X. D.， et al.， "Experimental Quantum Computing to Solve Systems of Linear Equations"， Phys. Rev. Lett.， 2013， 110， p. 230501.

[11]Schr?dinger， E.， Die gegenwarige situation in der quanenmechannik， Natürwissenschaften， 1935， 23： pp. 807-812， 823-828， 844-849.

[12]李承祖等：《量子通信和量子計算》，长沙：国防科技大学出版社，2000年，第118页。

[13]张文卓：《划时代的量子通信——写给世界第一颗量子科学实验卫星“墨子号”》，《物理》，2016年第9期，第553～560页。

[14]吴国林：《量子信息哲学》，北京：中国社会科学出版社，2011年，第38～39页。

[15]《列宁选集》第2卷，北京：人民出版社，1995年，第89页。

[16]夏立容：《信息与相互作用的关系》，《自然辩证法研究》，1995年第1期，第37页。

[17]顾小丰、孙世新、卢光辉：《计算复杂性》，北京：机械工业出版社，2005年，第13页。

[18]Deutsch， D.， "Quantum Theory， the Church-Turing Principle and the Universal Quantum Computer"， Proceedings of the Royal Society of London， 1985， 400， p. 98.

[19]吴国林：《超验与量子诠释》，《中国社会科学》，2019年第2期，第38～48页。

[20]Arute， F.， et al.， "Quantum supremacy using a programmable superconducting processor"， Nature， 2019， 574， pp. 505–510.

[21]Preskill， J.， "Quantum computing and the entanglement frontier"， http：//arXiv.org/abs/1203.5813 （2012）.

[22]Yang， B.， et al.， "Observation of gauge invariance in a 71-site Bose–Hubbard quantum simulator"， Nature， 2020， 587， pp. 392-396.

[23]Zhong， H. S.， et al.， "Quantum computational advantage using photons"， Science， 2020， 8770， pp. 1-9.

[24Omnes， R.， Quantum Philosophy， New Jersey： Princeton University Press， 1999， p. 150.

[25][奥地利]薛定谔：《薛定谔讲演录》，范岱年、胡新和译，北京：北京大学出版社，2007年，第99页。

[26]孙昌璞：《量子力学诠释问题》，《物理》，2017年第8期，第481页。

[27]吴国林：《波函数的实在性分析》，《哲学研究》，2012年第7期，第113～120、126页。

[28]这正是笔者作为首席专家主持2019年国家社科基金重大项目“当代量子诠释学研究”的重要缘由。

[29][30]爱因斯坦、波多耳斯基、罗森：《能认为量子力学对物理实在的描述是完备的吗？》，载《爱因斯坦文集》（增补本）第一卷，北京：商务印书馆，2009年，第460、461页。

[32][33]《爱因斯坦文集》（增补本）第一卷，北京：商务印书馆，2009年，第518、696页。

[34]吴国林：《哲學是什么？概念的创造、推理与系统化的学问》，科学网博客，http：//blog.sciencenet.cn/home.php？mod=space&uid=447363&do=blog&id=1280039，2021年4月17日访问。

[35]其中符号是直积，大致理解为矩阵的乘法或乘法。

[36]四个贝尔态表示为：

，

[37] 戴葵等：《量子信息技术引论》，长沙：国防科技大学出版社，2001年，第67～70页。

责 编/王亚敏（见习）

吴国林，华南理工大学哲学与科技高等研究所所长、科学技术哲学研究中心主任、教授、博导。研究方向为物理学哲学、超验科学哲学、分析技术哲学与量子诠释学。主要著作有《量子信息哲学》、《量子技术哲学》、《当代技术哲学的发展趋势研究》（合著）、《技术哲学研究》等。