求解大规模函数优化的粒子群优化算法
2021-06-28肖天宇张著洪
肖天宇,张著洪
(贵州大学 大数据与信息工程学院 贵州省系统优化与科学计算特色重点实验室,贵州 贵阳 550025)
0 引 言
受生物或自然现象启发的智能优化理论及应用作为人工智能的重要分支[1-3],在求解离散、连续或混合型偏低维优化问题方面,已发挥不可替代的作用,且近年不断涌现的新型智能优化算法为求解维度低于1000的偏高维优化问题的研究提供了启迪。可是,对于维度超过1000的大规模全局优化(large-scaled global optimization,LSGO)问题[4,5],因维度较高,性能指标的特性复杂,导致求解算法的性能退化严重[6]。由此,LSGO作为极为重要的科技难题已初步受到关注。
已报道求解LSGO的算法大致可概括为两类[6,7],即动态分群协同进化和群智能优化。前者是将决策变量动态划分为多个部分,各部分对应的子群独立进化,经由协同策略动态分配各子群,促使子群协同发现全局最优解[8-10];后者是一种基于现有群体智能优化算法的改进型优化方法,其具有潜在的并行性与分布式特点[11],搜索能力强,能克服分组策略“两步向前,合并向后”存在的不足[12]。可是,一旦决策变量不可分割或少许变量可分离时,算法的搜索效率急剧下降,种群的局部勘测和全局开采能力退化严重,因而算法极难获得全局最优解[6]。因此,如何有效权衡算法的开采与勘测能力,已成为求解LSGO的关键。
粒子群算法(particle swarm algorithm,PSO)自提出以来,因其结构简单、计算效率高等优点,获得研究人员的广泛关注。但是,PSO求解LSGO的效果并不理想,仍然存在收敛精度低、稳定性差、局部收敛等问题。为此,本文从如何提高和平衡PSO的开采与勘测能力出发,提出一种用于求解LSGO的新型粒子群优化算法(new particle swarm optimization algorithm,NPSO)。比较性的实验结果表明,NPSO在寻优质量方面具有优势,有潜在的应用价值。
1 问题描述与PSO的进化策略
1.1 问题描述与PSO的基本更新策略
考虑如下大规模单目标全局函数优化问题
minf(x)=f(x1,x2,…,xD)xi∈[ai,bi],1≤i≤D
式中:f(x)关于x连续,xi为决策变量,D≥1000。
PSO是一种源于鸟类迁徙过程且结构简单、搜索效率高、进化能力极大依赖于学习率的寻优算法,已广泛被应用于工程领域[13-15]。其将优化问题的每个解看成一个粒子,通过种群中粒子不断进行信息交互,以及借助个体最优位置xpbest和全局最优位置xgbest引导粒子移动,促成最终获得最优解。基本的PSO的粒子更新方式如下
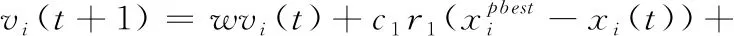
(1)
xi(t+1)=xi(t)+vi(t+1)
(2)
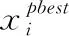
理论分析表明,PSO在处理低维优化问题时,能兼顾勘测与开采能力,但当问题的维数较高时,因搜索空间成指数级增长,导致PSO的搜索效率急剧下降且极易陷入局部搜索,以及普适性下降[16]。因此,如何增强PSO处理LSGO问题的勘测与开采能力,是本文研究的重点。
1.2 劣质粒子学习
给定全局最优粒子xgbest以及2m个粒子x1,x2,…,x2m。假定粒子xi的适应度不低于粒子xi+1的适应度;将前m个粒子视为优质粒子,而后m个粒子视为劣质粒子;粒子xm+i借助xgbest对称地向优质粒子xi学习,并执行更新,即
xm+i,j(t+1)=xm+i,j(t)+vm+i,j(t+1)
(3)
在此
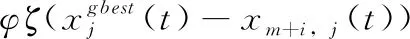
(4)
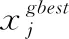
在PSO中,由于xgbest的影响,在迭代后期,xpbest很可能与xgbest较为靠近,因此会造成群体多样性丧失,使算法陷入局部搜索[17]。通过上述“对称学习”策略,用群体中较好粒子取代PSO中粒子的历史最好位置,使粒子不再单一地向粒子历史最优解学习;粒子间不断进行信息交互,充分利用群体信息,增强粒子学习的多选择性,保证粒子不向单一方向转移,增强算法的全局搜索能力;同时,利用全局最优粒子引导粒子进化,提升算法的收敛速度,达到全局寻优的目的。
1.3 粒子的位置扰动
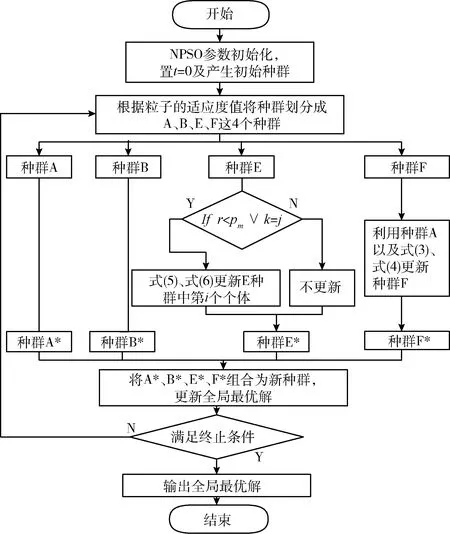
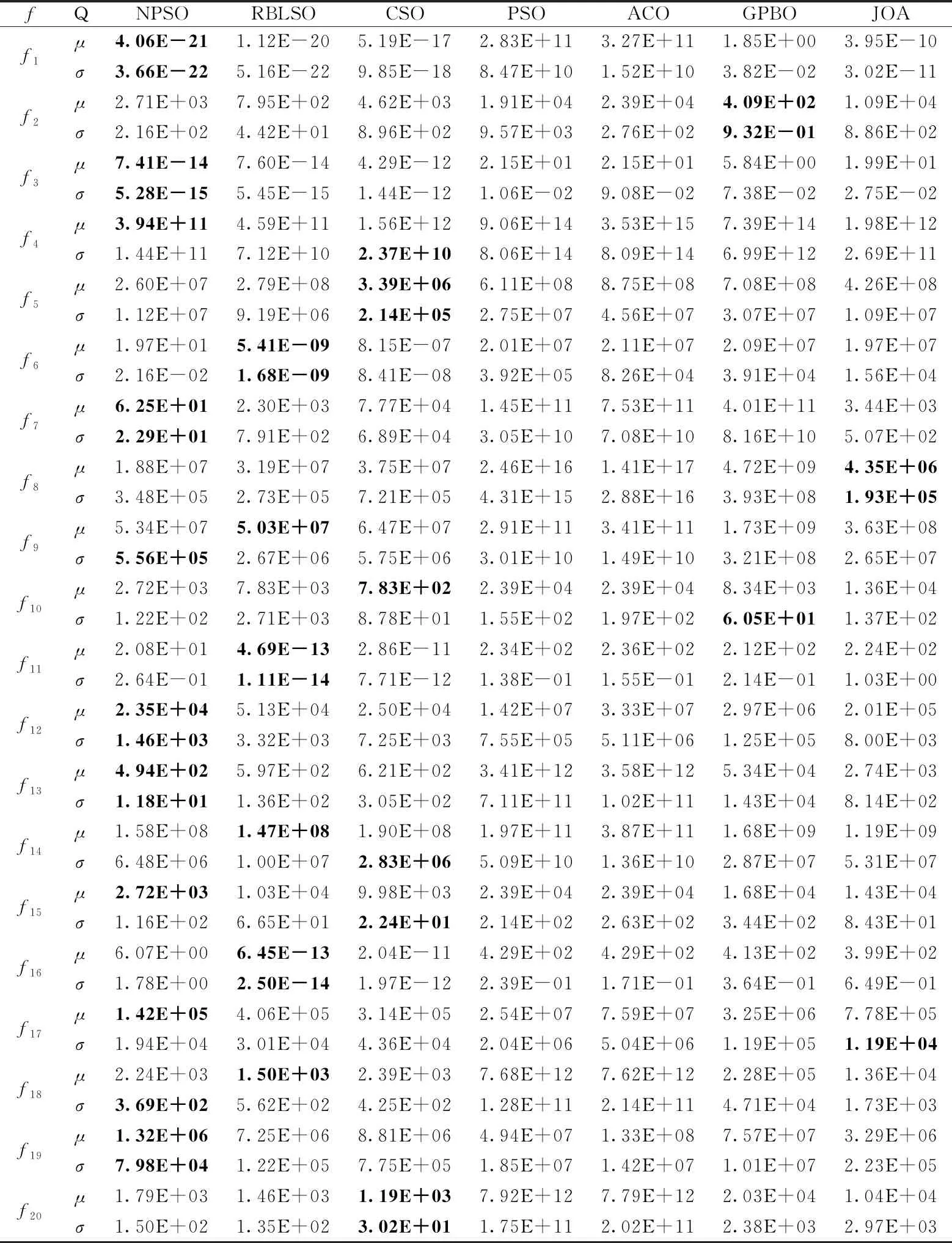
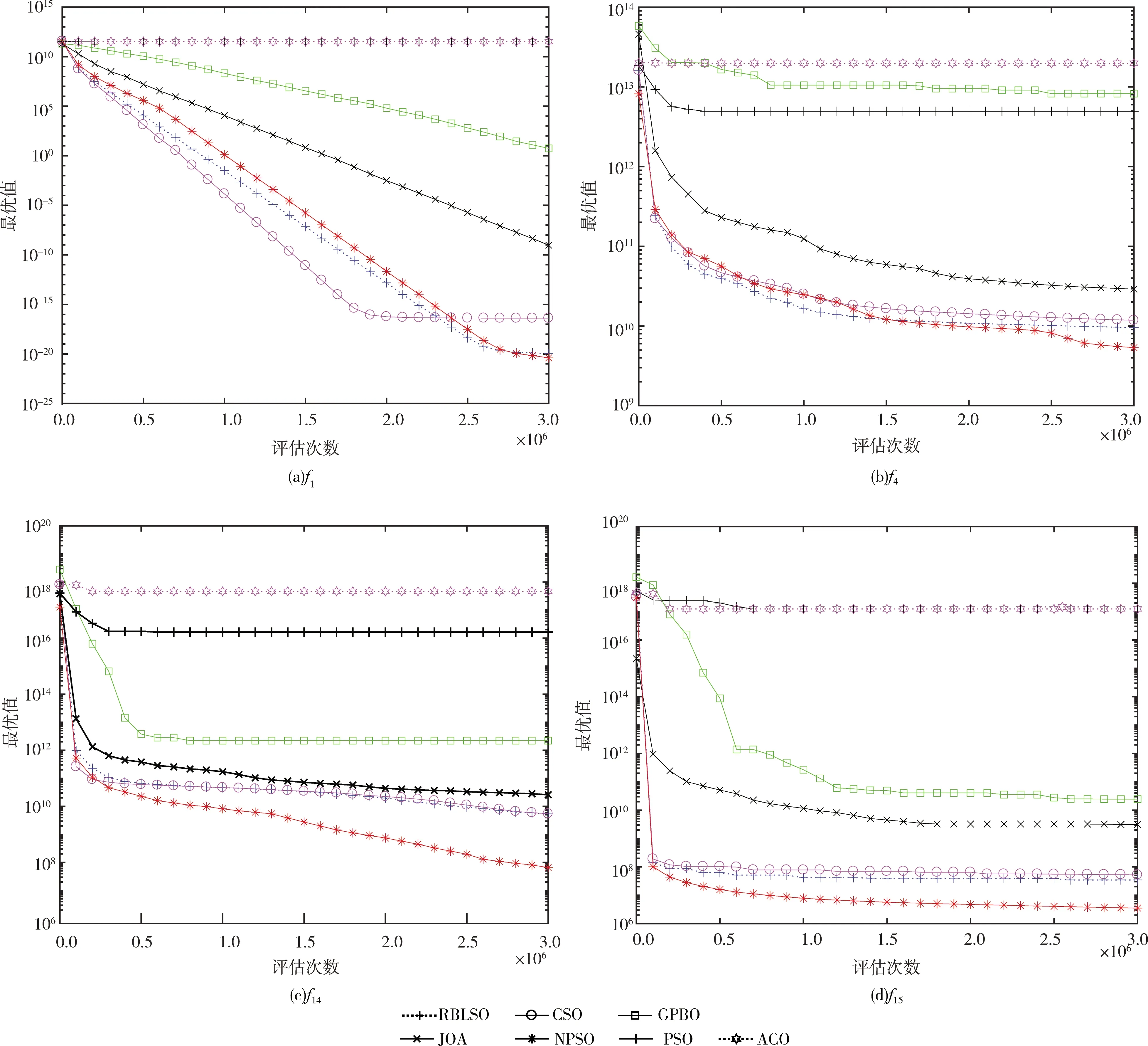
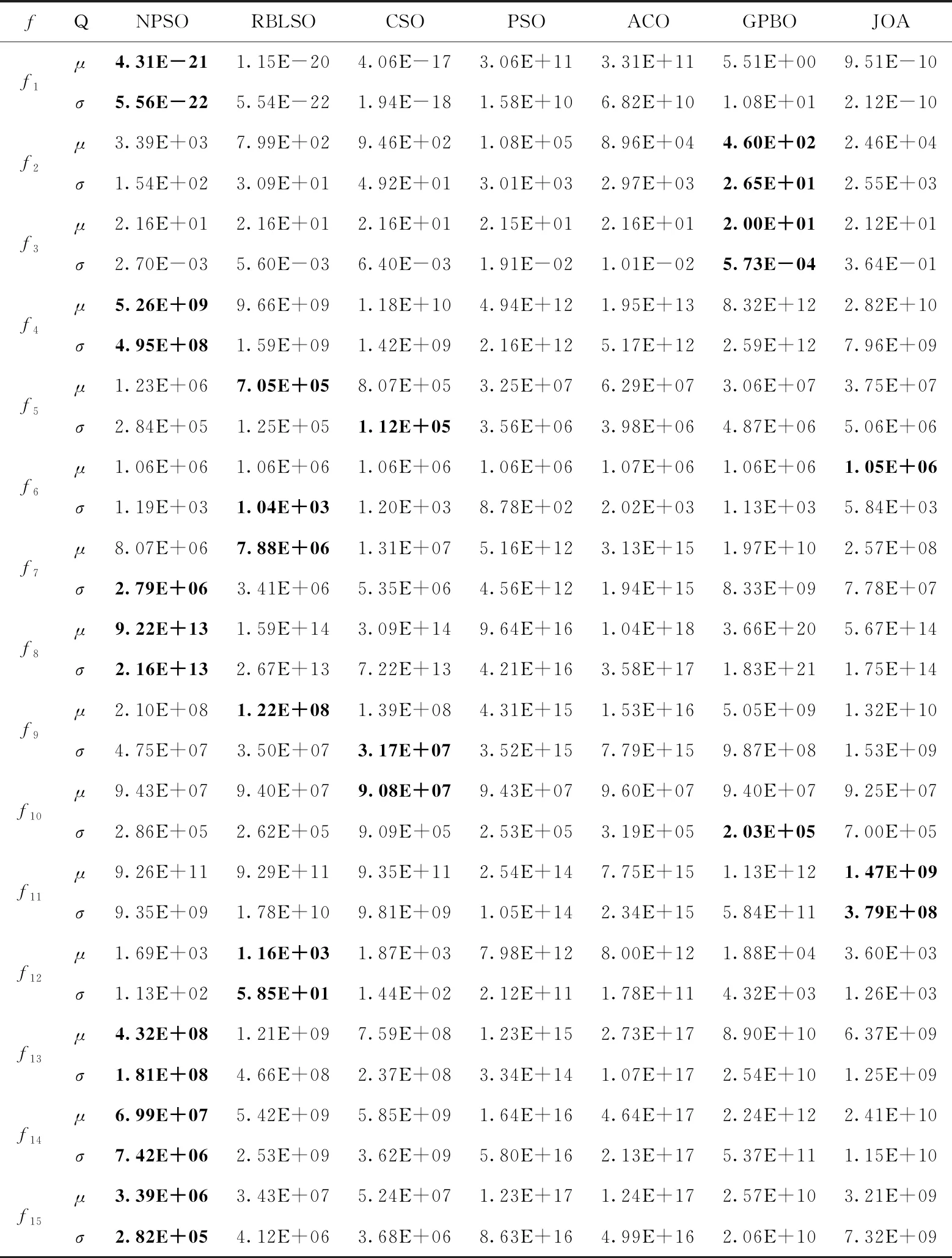
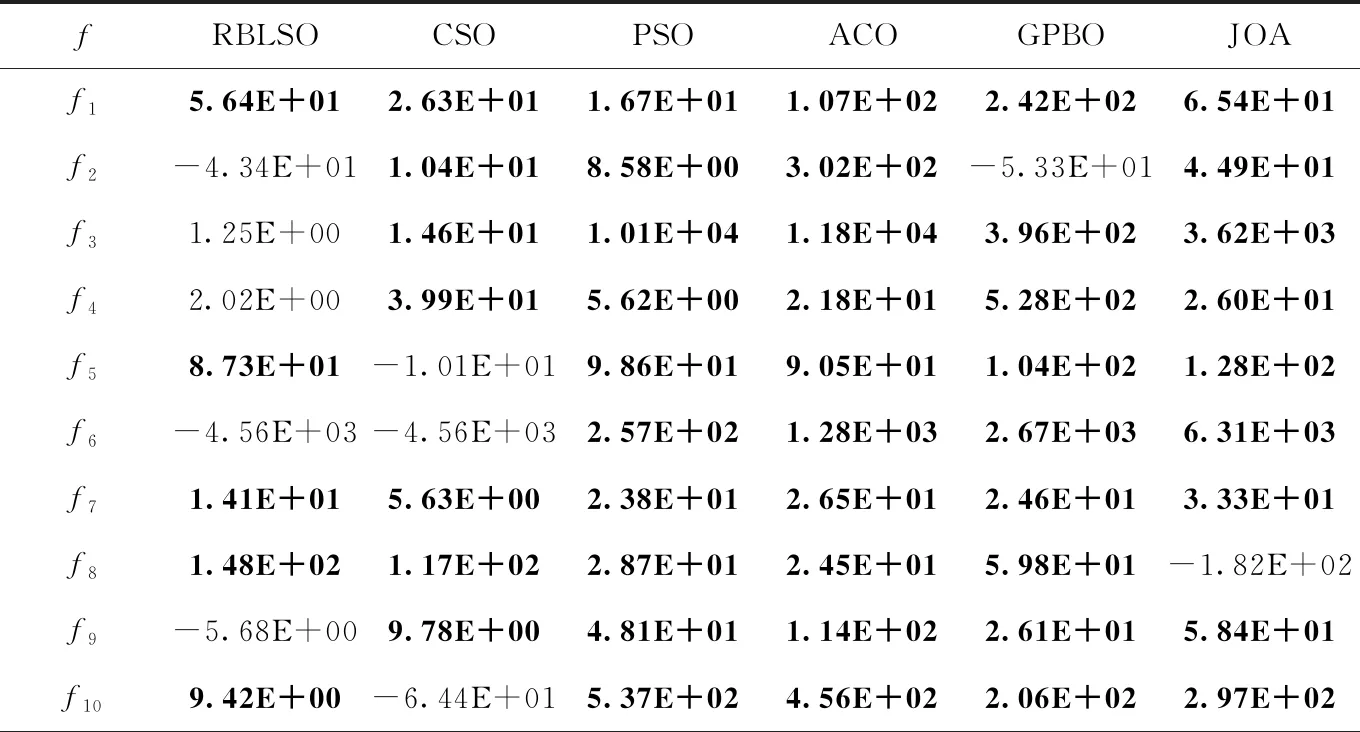
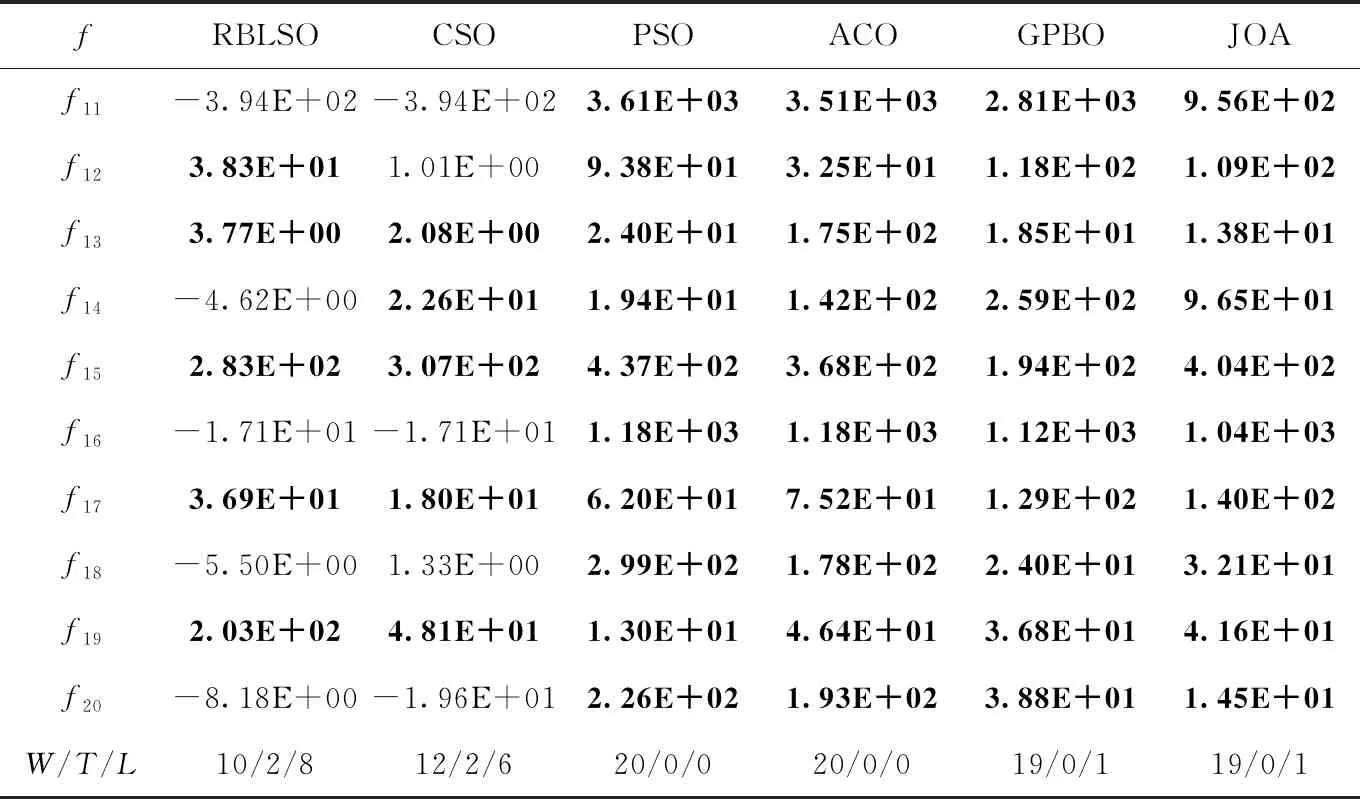
给定以上最优粒子xgbest以及m个粒子x1,x2,x3,…,xm,xi在xgbest的引导下,依据变异概率pm对xi中第j个维度分量进行高斯扰动,即当1~D之间的随机数k=j或者r xi,j(t+1)=xi,j(t)+vi,j(t+1) (5) 其中 (6) 在以上位置扰动策略下,粒子依概率或者依维度确定位置是否更新,同时利用最优粒子和需更新的粒子的位置偏差,对需更新的位置进行高斯扰动,确保每个粒子每次至少有一个分量发生改变,使粒子每次搜索都在xgbest附近进行,防止无效搜索,增强粒子的局部勘测能力。粒子通过自适应地调整其搜索范围,防止因搜索范围偏大而跳过最优解的位置。此策略可消除原PSO中粒子更新过度对xpbest的依赖,增强粒子的局部搜索能力。 NPSO主要由粒子群分割与更新两个模块组成,如图1所示。前者根据当前粒子群中粒子的适应度,将粒子群划分为精英种群(A)、优质种群(B)、中等种群(E)、劣质种群(F)。各种群经由粒子的历史信息和特定的更新策略产生新粒子群。 结合第1节的模块设计和图1,NPSO的具体描述如下: 图1 NPSO算法流程 (1)输入参数:种群规模N,维度D,最大迭代数Gmax,位置更新概率pm,学习率φ; (2)置t←1,随机生成规模为N的初始粒子群P(t),其最好粒子记作xgbest; (3)按粒子适应度对P(t)中粒子进行降序排列后,前N/4个粒子构成种群A,随后N/4个粒子构成种群B;依此类推,获规模为N/4的种群E和F; (4)种群A、B、E、F分别执行如下更新步骤: 1)依据种群A及xgbest,利用第1.2节的劣质粒子学习策略,对种群F中各粒子进行更新; 2)依据xgbest及位置更新概率pm,利用第1.3节的粒子位置扰动策略,对种群E中各粒子更新; 3)组合种群A、B及更新后的种群E、F为粒子群P(t+1),更新xgbest; (5)t←t+1;若t 以上算法设计中,种群A引导种群F进行更新,促使种群中粒子间信息交互,增强算法的全局开采能力;种群B并不直接参与进化,其目的在于防止在每次迭代中由于粒子重复更新而导致算法陷入局部搜索;种群E中的粒子依概率及高斯变异策略执行局部搜索,防止因粒子的大量位置更新而导致劣质粒子变得更差,增强算法的局部勘测能力。该算法的结构简单,易于实现,且兼顾群体勘测与开采对获取全局最优解的贡献;同时,在优质粒子引导下,劣质粒子经对称学习逐渐变为优质粒子。 在NPSO中,算法的计算复杂度主要由步骤(3)、步骤(4)决定。在一个迭代周期内,步骤(3)需对粒子进行排序,其计算复杂度为O(NlogN);步骤(4)需对种群E和F中的粒子进行更新以及计算适应度,其至多执行(N(D+1)/2)次。因此,在最坏情形,NPSO的计算复杂度为O(N(logN+(D+1)/2))。此表明,N和D是影响算法效率的关键因素。 在Windows 10/CPU 3.30 GHz/RAM 8.0 GB/ Visual Studio 2013环境下展开数值实验。为比较分析NPSO的性能,将其与6种不同的算法进行比较,即基于种群竞争学习的粒子群算法(CSO)[17]、基于偏置中心学习的粒子群算法(RBLSO)[18]、经典粒子群算法(PSO)、蚁群优化算法(ACO)、联合操作算法(JOA)[19]、气体扩散算法(GPBO)[20]。上述对比算法的详细参数设置以及本文的参数设置见表1。测试事例为文献[17]中CEC′2010和CEC′2013测试集,共计35个可分解、部分可分解、不可分解的LSGO最小化问题,其中CEC′2010包含20个测试函数,CEC′2013包含15个测试函数,每个问题的维度D均为1000;测试事例的目标函数的特征见表2。 表1 各算法参数设置 各算法对每个测试问题均独立运行25次,每次的最大适应度评价次数均为3×106;每种算法求解每个测试问题25次后,获得的25个最好目标值被用于算法比较分析。为充分呈现NPSO的性能,算法的比较分析包括:①研究以上算法求解表2中测试问题的性能差异;②借助假设检验分析算法的搜索效果是否存在显著性差异。 表2 测试函数特性 情形1:CEC′2010测试集 将以上每种算法作用于CEC′2010测试集中每种测试问题25次后,获得的统计结果见表3,其中μ代表25个最优值的均值,σ代表25个最优值的标准差;以f1、f4、f15、和f19为例,各算法的平均搜索曲线如图2所示。 表3 算法求解CEC′2010测试问题获得的统计结果比较 经由表3可知,NPSO与RBLSO、CSO和PSO相比,其求解以上表2中CEC′2010的20个测试问题,能分别获得12、14、20个最小均值以及11、11、18个最小均方差;从函数特性上看,无论对哪种测试函数,NPSO获得的解质量都要好于PSO的解质量;与两种改进型粒子群算法RBLSO和CSO相比,NPSO求解单模态(如f1、f7)以及可分函数(如f12、f13)的寻优效果要好。当其与新型算法GPBO、JOA及传统算法ACO相比,能分别获得19、19、20个最小均值以及16、15、18个最小均方差,可以看出,NPSO获得的解质量都要好于这3种算法。 图2表明,NPSO的改进型策略能有效地克服PSO易陷入局部搜索的不足,同时可兼顾勘测与开采的能力。图2(a)表明,对于单模态可分函数f1,PSO在搜寻初期就已陷入局部最优,而NPSO不仅未陷入局部最优,而且拥有较快的收敛速度以及较高的收敛精度。NPSO与RBLSO、CSO相比,其虽然在搜寻初期的收敛速度略慢,但其局部寻优能力较强。它在迭代中期以及后期的收敛速度较快,同时可以在迭代后期能有效防止陷入局部搜索。结合表3中的统计结果可知,NPSO不仅对单模态函数(如f1、f7)的寻优能力较强,而且对多模态函数(f13、f15)、完全不可分函数(如f19)这类较复杂的函数都有较强寻优能力,且易于跳出局部搜索。 情形2:CEC′2013测试集 类似于以上情形1的数值实验,各算法求解CEC′2013测试集中每种测试问题25次后,获得的统计结果见表4;以f1、f4、f14和f15为例,各算法获得的目标值的平均搜索曲线如图3所示。 经由表4,NPSO与RBLSO、CSO及PSO相比,其分别获得7、9、14个最小均值和8、12、13个最小均方差;与GPBO、JOA和ACO相比,其分别获得11、11、15个最小均值与11、14、15个最小均方差。结合表3中的实验结果,NPSO对于15个单模态函数,求解其中13个函数具有优势;对于20个多模态函数,其求解其中5个函数具有优势。此表明,NPSO求解单模态LSGO问题比求解多模态LSGO问题更有优势。这是因为算法在迭代过程中多次使用全局最优粒子引导种群粒子进化,粒子逐渐靠近全局最优粒子,因此对单模态问题具有潜力。对于较难的3个完全不可分问题以及3个重叠问题,NPSO分别获得2、2个最小均值与标准差,并且结合图3中的收敛曲线,NPSO在解决更为复杂的完全不可分问题以及重叠问题时,已初步具有一定的优势。如图3(d)所示,对于完全不可分函数f15,虽然NPSO在迭代初期与RBLSO和CSO的下降速度大致相同,但随迭代数的增大,RBLSO与CSO的收敛速度变慢,NPSO仍然保持较快收敛速度,而PSO却快速陷入局部搜索。 图3 算法求解f1、f4、f14、f15的平均搜索曲线比较 表4 算法求解CEC′2013测试问题获得的统计结果比较 为分析以上7种算法求解CEC′2010、CEC′2013中测试问题后获得的解是否存在显著性差异,将得到的解的目标值作为样本值进行t检验。通过取显著性水平α=0.05,获得的t检验结果见表5、表6,表中W、T、L分别指NPSO在求解测试问题上表现较好、相等以及较差的个数。 表5 算法求解CEC′2010测试集的t检验结果比较 表5(续) 表6 算法求解CEC′2013 测试集的t检验结果比较 经由表5、表6可知,针对CEC′2010、CEC′2013测试集的35个测试问题,NPSO依次与RBLSO、CSO、GPBO、JOA、PSO及ACO相比,能获得最好效果的问题个数依次是16、21、28、30、31及34。因此,NPSO较参与比较的6种算法在获得的解质量方面具有明显优势。 鉴于LSGO是智能优化未来研究的重点分支,以及LSGO属于极具挑战性的研究课题,本文从粒子群优化角度,围绕粒子的学习效果提升、多样性增强问题,借助粒子对称学习、高斯变异,设计劣质粒子学习、粒子位置扰动策略,获得适合于求解LSGO的新型粒子群优化算法(NPSO)。理论分析表明,该算法的计算复杂度由粒子群规模和优化问题的维度确定。比较性的实验分析表明,NPSO在相同的最大粒子评价次数下,在求解质量方面具有明显优势。另外,虽然NPSO求解单模态LSGO问题的优势较为突出,但求解多模态LSGO问题时,其局部勘测能力仍有提升空间,这也是未来努力的研究方向。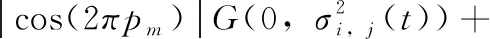
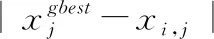
2 算法的原理与设计
3 数值实验


3.1 实验结果与比较分析
3.2 显著性检验

4 结束语
