基于KPCA和K-Means++的秦岭植被变化检测

申少格，杨渭清，杨绍静

（西安文理学院信息工程学院，陕西西安，710065）

0 引言

本文利用遥感技术获取秦岭生态环境变化的基本数据，如森林覆盖状况变化、土地利用变化、湿地资源状况变化等，结合相应算法和模型，为保护秦岭措施提供评估依据。

故而遥感动态监测方法显得尤为重要，从不同时期的遥感数据中，定量的分析和确定地表变化特征与过程，它涉及到变化的类型、分布状况与变化量，即需要确定变化前后的植被覆盖率、界限即变化趋势，能提供地物的空间分布及其变化的定性和定量分析。它主要包括数据源选择，图像输入与浏览，图像预处理，图像信息提取，成果报告与应用等过程。在此，本文主要研究图像信息提取，采用先进的KPCA算法和K-Means++算法进行优化，来得到更优结果。具体过程如图1所示。

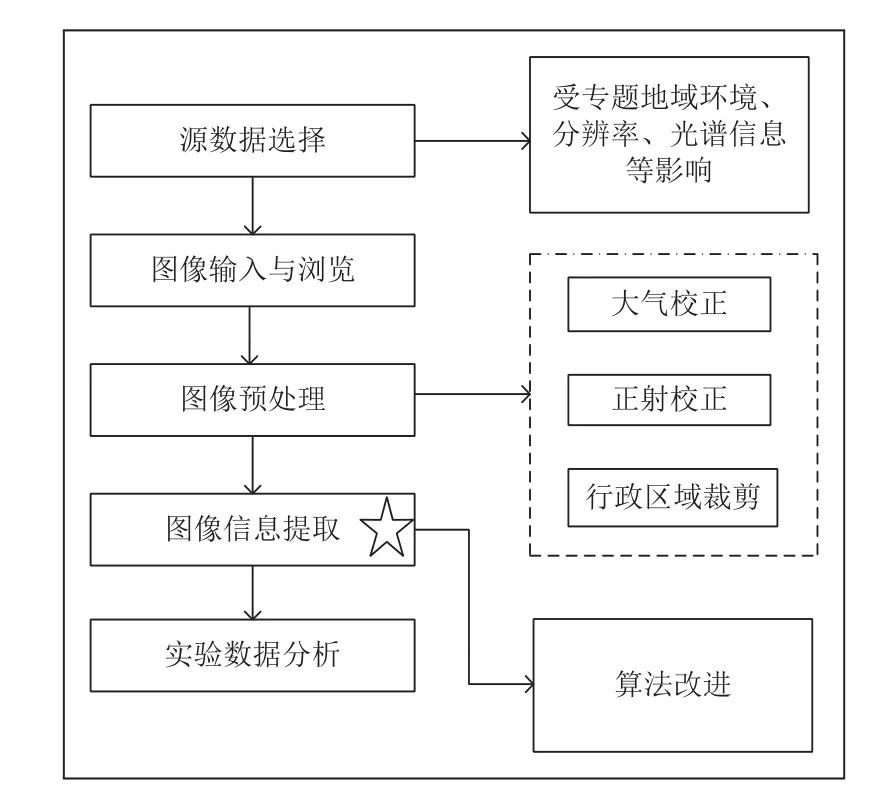
图1 植被动态变化监测过程

1 数据预处理

在研究图像信息提取前，本文首先对所下载的图像进行预处理等操作，将图像的数字量化值（DN）转化为辐射亮度值域，改变其地类波谱曲线，并通过大气校正将反射信息从大气和太阳的信息中分离出来，消除其对地物反射的影响，根据RMSE与SE关系判断是否需要几何校正，最后再进行行政区域裁剪，将研究之外的区域去除[2]。

2 图像信息提取

遥感影像通过亮度值或像元值的高低差异（反应地物的光谱信息）及空间变化（反应地物的空间信息）来表示不同地物的差异，这是区分不同影像地物的物理基础。遥感影像分类是利用计算机通过对遥感影像中的各地地物的光谱信息和空间信息进行分析、选择特征，将图像中的每个像元按照某种规则或算法划分为不同的类别，然后获得遥感影像中与实际地物的对应信息，从而实现遥感影像的分类，即信息提取。遥感图像信息提取又包括人工解译、自动分类、特征提取、动态监测、反馈、高程提取等过程。本文主要对分类算法进行改进，将传统的PCA算法改为KPCA，将K-Means算法改为K-Means++[3]。

2.1 传统PCA方法

首先考虑在一维向量(M=1)上的投影，此时映射向量U的大小为D*1，用u1代替，同时设置，(因为我们只对u1的方向感兴趣，对其大小不感兴趣)。数据点xn被投影到上，投影数据的均值为。其中为样本的均值:

也就是说，我们将u1设置为矩阵S的最大特征值1λ所对应的特征向量时，此时投影数据的方差有最大值，此特征向量也被称为第一主成分。同理，我们可以用一种增量的方式定义额外的主成分，方法为:在所有与那些已经考虑过的方向正交的所有可能方向中，将新的方向选择为最大化投影的方向。简单的说就是考虑矩阵S前M特征向量，组成映射矩阵U

2.2 改进PCA算法

核主成分分析（KPCA）[4]是在传统PCA的基础上，为了更好的图区适合分类的特征，提出的一种改进算法，它是通过某种隐式方法将输入数据映射到特征空间F，并在特征空间中实现统计主元分析，进而有效的提取非线性特征。

根据（10）式和（12）式分别计算投用主分量和特征向量。

设测试样本为x，则其在vj上得投影。

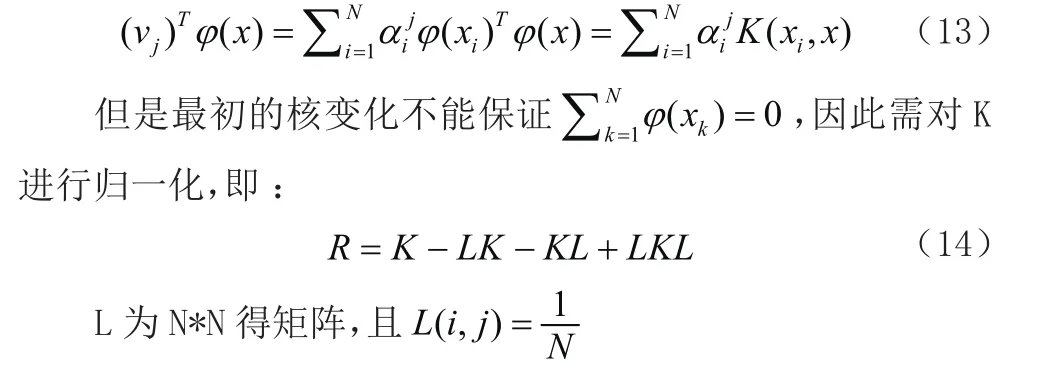
2.3 K-Means与K-Means++

K-Means使用聚类分析方法，随机的查找聚类簇的聚类相似度相近，即中心位置，是利用各聚类中对象的均值所获得一个“中心对象”（引力中心）来进行计算的，然后迭代地重新配置他们，完成分类过程。

但是在使用K-Means进行特征聚类的过程中发现，K-Means随机选取初始聚类中心，导致每次聚类所产生的结果不同，导致算法收敛很慢甚至出现聚类出错的情况[5]。

由于秦岭地区的植被类型多样、物种丰富，所以随机选取聚类中心对于秦岭地区的植被变化检测研究存在很大的局限性。然而在K-Means基础上改进的K-Means++方法能够使初始聚类中心尽可能的分散开，有效的减少迭代次数，加快了运算速度[6]。

因此我们选择K-Means++方法对特征提取后的数据进行特征聚类。

3 实验数据分析

为了进一步确认改良方法的正确性，选择西安秦岭北麓2013年和2017年的图像，在对图像进行预处理之后，我们首先采用传统的PCA算法，对信息进行分类提取，如图2所示。

图2 主成分分析动态监测结果

再采用改良算法KPCA和K-Means++对预处理的数据进行信息分类提取。如图3所示。

图3 改进方法后动态监测结果

根据图2和图3的结果，首先可进行目视对比法对比，其次，我们使用计算机技术，对两次图形信息进行分类提取，结果如图4所示。

图4 原始方法与改进方法对比图

由实验结果可看出，改进的方法得出的图像像元更加精细，处理结果更加明显。能够更加精准的反映秦岭植被动态变化，为秦岭生态保护提供更加可靠的依据。

4 结束语

本文基于PCA和K-Means算法设计出改进之后的KPCA及K-Means++算法，对采集的数据进行信息分类提取，并对提取的信息进行变化检测。将输入数据映射到特征空间F，并在特征空间中统计主元。实验结果显示，改进的算法提高了准确度。运用于实际更加有利。