关于电功率与器件储能和作用力的有条件叠加性讨论

陈希有, 齐 琛, 李冠林, 牟宪民

(大连理工大学 电气工程学院，辽宁 大连 116023)

0 引言

叠加定理是电路课程的重要教学内容之一。在讲到这个定理时，几乎无一例外地要特别强调，功率与电压或电流不是线性关系，不能按叠加定理计算电路消耗的总功率。由此这一论断便在学生思想中早早地固定下来，先入为主，只要遇到计算功率的问题，都不敢使用叠加定理。然而，事实并非如此，不能一概而论。对某些特殊电路，完全可以按照叠加定理的步骤计算多个电源共同作用时产生的总功率。一些作者对此已经有所研究。文献[1]、[2]，基于纯电阻电路，使用特勒根定理证明了一个普遍规律：电压源组和电流源组共同作用产生的总功率，等于这两组电源按组单独作用时，分别产生的总功率的叠加。文献[3]证明了，当两个独立电源在某阻抗上产生的电流相位相差90度时，它们共同作用在阻抗上产生的总有功功率和总无功功率都满足叠加定理。文献[1]、[4]较详细地讨论了多频电路平均功率满足叠加定理的问题。

本文进一步列举一些特殊电路，证明了在这些特殊电路中，是可以按照叠加定理的步骤来计算总功率的。在教学中，一般都较早地讲授叠加定理，当时还不具备必要的基础来联系这些特殊电路。但在后续的教学内容中，应该恰如时机地修正功率不满足叠加定理的绝对论断。

将本文列举的某些特殊电路用于教学，或留作启发性思考，可以培养学生敢于质疑的科学精神，以及具体问题具体分析的认识论观点；站在更高度的系统观点认识电路问题，而不仅仅是站在以某个电压或电流为激励或响应的较狭隘观点。

1 电源非对称三相电路功率的叠加性

根据对称分量法，非对称的三相电源可以分解成正序、负序和零序三组对称分量(本文不介绍分解方法，可以参见早期电路教材，例如文献[5]，或“电力系统分析”课程教材)。计算时可以让三个序分量单独作用，每个序分量单独作用时，都是对称三相电路。

为简便，假设系统无中线，这样可以忽略零序电流。对有零序电流的情况，下面的结论也是正确的。将负载上非对称的瞬时相电压和相电流分别用向量u和i来表示，并表达成正序分量与负序分量之和的形式，即

经计算，二者内积即三相负载总瞬时功率为

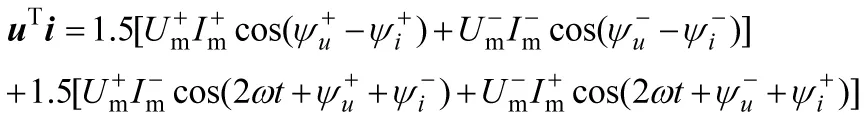
上式第二行中的两项功率都是时间的余弦函数，并且角频率是电源角频率的2倍，因此在一个电源周期内的积分必然都是零。剩下第一行中的两项，分别是正序电源和负序电源单独作用产生的瞬时功率，这些功率是常量，因此也是平均功率。由此得出结论：

正序电源和负序电源共同作用产生的三相平均功率，等于它们单独作用时产生的三相平均功率的叠加。

出现这种叠加形式是由于不同相序的电压和电流不形成平均功率的缘故。如果讨论的是瞬时功率，情况就不同了，因为任何相序关系的电压和电流都可以形成瞬时功率，因而不能用叠加的方法来计算三相瞬时功率。

在这个特例中，将正序和负序电源分别看作是系统的输入，而将三相平均功率看作是系统的一种输出。

2 多频稳态电路功率的叠加性

多频稳态电路是指电路中含有多个不同频率正弦电源的电路。这些不同的频率又区分成频率成整数倍关系(例如傅里叶展开后对应的谐波电源)，以及频率虽不成整数倍关系，但倍数为有理分数两种情况。对前者，总平均功率等于各不同频率电源单独作用产生的平均功率的叠加，这几乎是电路类教材中都提到的结论；对后者，文献[1]和[2]已有详细分析，其结论与前者是一样的。需补充说明的是，总平均功率是指在这些电源公共周期内的平均功率。本文对此不再重述，只是作为功率满足叠加性的一个方面稍作提及。

3 多频稳态电路中平均储能和平均作用力的叠加性

众所周知，在多频稳态电路中，电压或电流有效值的平方，等于各不同频率电源单独作用时，产生的电压或电流有效值的平方和。也就是说，电压或电流有效值的平方满足叠加性。这样，凡是与电压或电流有效值平方成正比的量也就都满足叠加性。例如，在多频稳态电路中，电容储能是周期变化的，其平均值可按下式计算：

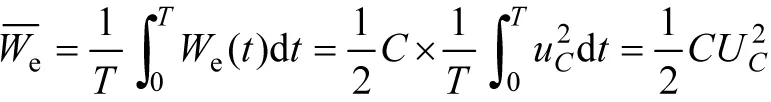
它正比与电容电压有效值的平方。因此得出结论：

在多频稳态电路中，电容储能的平均值，等于各不同频率电源单独作用时，在电容上产生的储能平均值的叠加。

对电感也有类似结论，这是因为

在这两个特例中，将储能元件的平均储能看作是系统的一种输出。

再例如，当平板电容极板之间存在电压uC时，如图1所示，两个极板之间便存在吸引力，给出这个力大小的计算公式如下[6]：

图1 平板电容受力分析

该导数可以根据平板电容的计算公式来获得。

如果在极板之间施加的是周期电压，则极板之间的吸引力也是周期的。在电压的一个周期内，吸引力(极板固定)的平均值是

它正比与电容电压有效值的平方。因此得出结论：

在多频稳态电路中，电容极板之间的平均吸引力，等于各不同频率电源单独作用时，在极板上产生的平均吸引力的叠加。

同理，如果两个互感线圈串联，从而流过相同电流，如图2所示，那么两个线圈之间的电磁作用力(吸引或排斥，取决于磁场方向)的瞬时值为

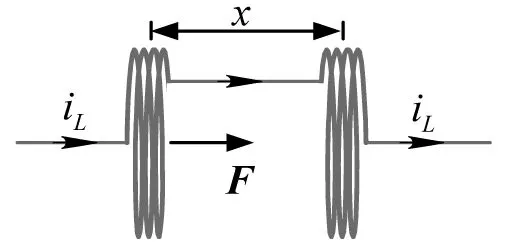
图2 互感线圈受力情况

式中M代表互感，它与线圈之间的距离x有关。可以通过互感系数的计算公式来求得该导数。

如果使线圈通过的是多频稳态电流，线圈之间的作用力必然是周期变化的。在一个周期内，作用力(线圈固定)的平均值是

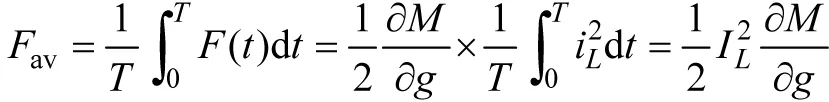
它正比与线圈电流有效值的平方，因此也满足叠加性。

在上述两个特例中，将作用力看作系统的一种输出。

4 二端口网络功率的叠加性

如果电阻性互易二端口网络两个端口分别接入电流源和电压源，互易网络可以用T形电路来等效，得到图3所示等效电路。

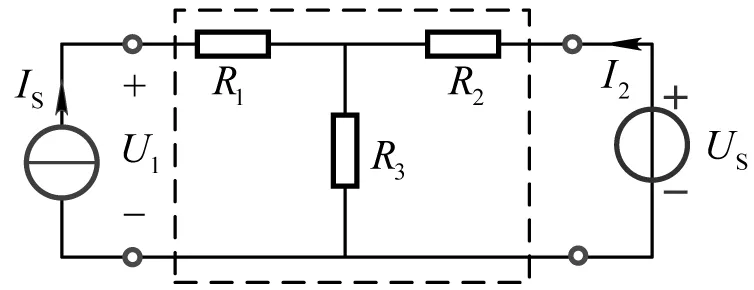
图3 讨论二端口网络功率的叠加性

利用叠加定理可以写出端口电压和电流之间的关系：

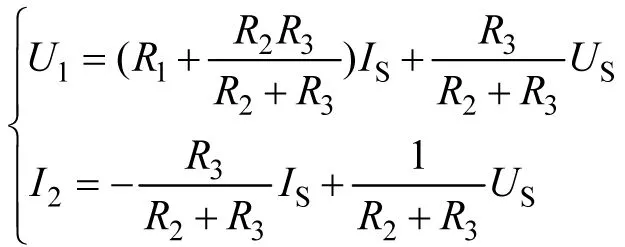
因此，二端口网络从两个端口消耗的功率分别为

将上述两个功率相加就是二端口网络消耗的总功率。然而，相加后，对应USIS的两项因符号相反而刚好抵消，所以总功率表达式简化成下式：

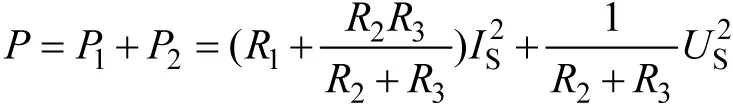
这两项显然就是电流源与电压源单独作用时，二端口网络消耗的功率。由此得出结论：

对电阻性互易二端口网络，两个端口分别连接电流源和电压源，由这两个电源共同作用导致二端口网络消耗的功率，等于它们分别单独作用时，二端口网络消耗功率的叠加。

关于二端口及多端口网络功率叠加性的更多问题，笔者将另文讨论。

5 无损均匀线传输功率的叠加性

分暂态和稳态两种情况。先设无损均匀线两端各接入一个阶跃电压源，分别产生正向行波和反向行波，如图4所示。在产生反射之前，于它们相遇处线上的电压和电流分别为两个方向行波的叠加，即

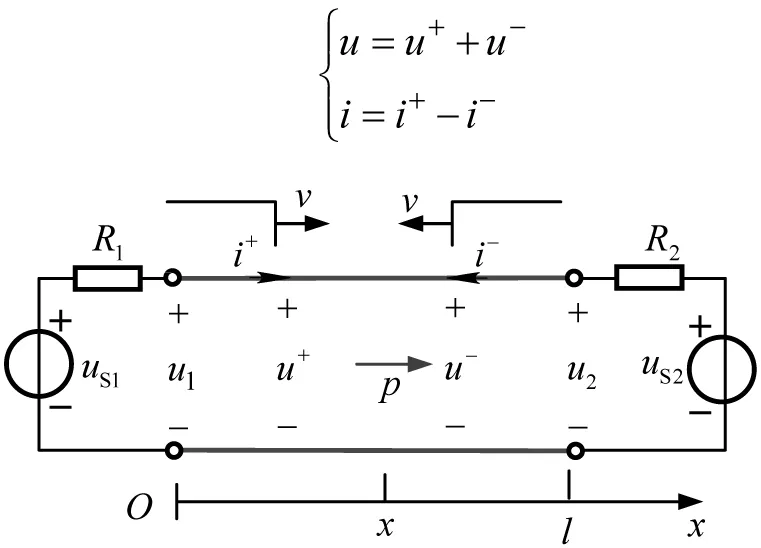
图4 无损线两端接阶跃电源

因此，沿x方向传输的功率为

由于无损线行波之间满足u+=Zci+，u-=Zci-，所以上式括号中的交叉乘积项之差为零，即

这说明，两对不同方向的电压与电流产生的瞬时传输功率相互抵消。这样便得出结论：

两个电源共同作用在正向行波和反向行波相遇处产生的瞬时传输功率，等于两个电源单独作用时，在该处产生的瞬时传输功率的叠加。

再讨论正弦稳态情况，以下可以证明，当线路两端所接电阻(或电源内阻)相等时，两个电源在无损线上产生的传输功率也有条件地满足叠加性。这又分下面三种具体情况，电路连接如图5所示。

图5 讨论无损线传输功率满足叠加性的电路

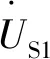
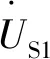
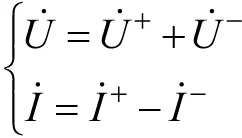
因此，沿线向x方向传输的平均功率为

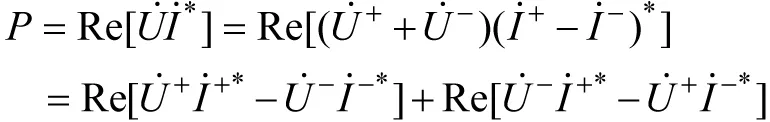
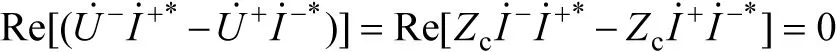
这说明，两对不同方向的行波电压与电流形成的平均功率相互抵消。结果得到

(1)

由此得出结论：两端均匹配时，两个电源在两端共同作用，沿无损线传输的平均功率，等于两个电源单独作用时，沿无损线传输的平均功率的叠加。

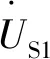
因为是无损线，线上传输的平均功率处处相同，因此可以取线路中间位置来分析，并用戴维南定理等效左右两部分，得到图6所示的集中参数等效电路。图中等效阻抗按均匀传输线公式来计算：

图6 计算线路中间位置电压电流的等效电路

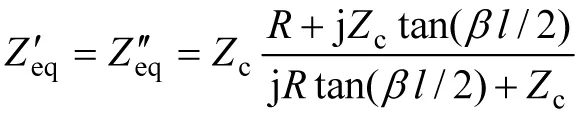
线路中间位置电压与电流分别为：

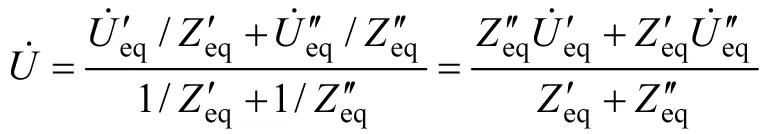
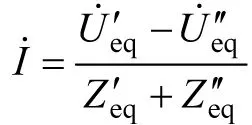
因此，沿线向x方向传输的复功率为

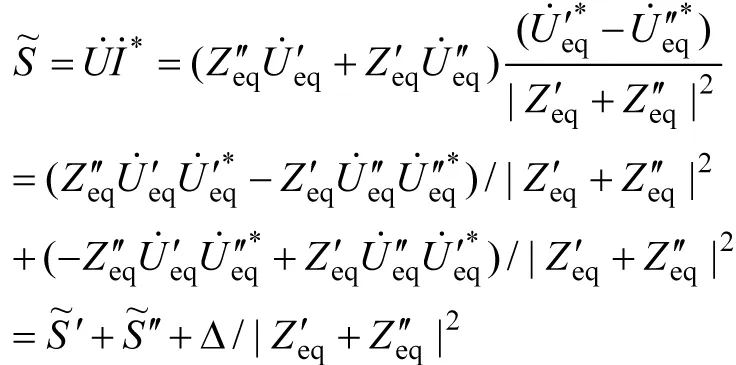
(2)

由此得

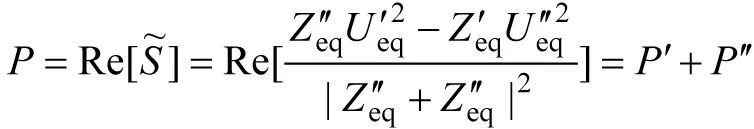
(3)

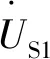
P"同理，略。

(3)当R1=R2=R≠Zc，且两个电源大小和相位差任意时，对特定长度的无损线，线上传输的功率也满足叠加性。特定的长度是l=mπ/β，其中m为正整数。论证如下：m为奇数时，等效阻抗为

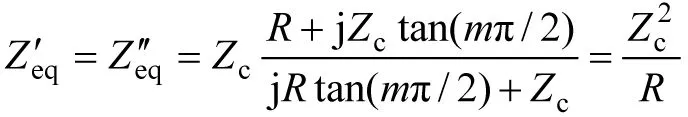
m为偶数时，等效阻抗为

它们共同的重要特征是等效阻抗为实数。仍取线路中间位置进行分析。不难验证式(2)中交叉乘积项之差的实部为零，即

所以式(3)仍然成立，即无损线上传输的功率满足叠加性。

6 计算举例

仅就均匀传输线稳态情况举例如下。已知条件是Zc=377 Ω，β=10-5/km，R1=R2=R。其他条件分4种情况，对应计算结果如表1所示。全部是用传输线方程计算所得，而不是使用集中参数等效电路。表中电压、电阻、功率单位分别为V、Ω和W。表中第1行数据对应R=Zc，两个电源可以是任意相位关系；第2行对应R≠Zc，但两个电源需要满足同相位关系；第3行对应R≠Zc、两个电源可以是任意相位关系，但长度须是mπ/β；第4行对应线长为3.3π/β，其他同第3行。除第4种情况外，其他情况的功率都在所限定条件下满足叠加性。

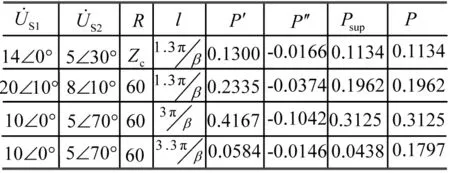
表1 无损线传输功率的叠加性举例

7 结语

(1)存在正序、负序与零序电源电路、多频电源电路、无损线暂态和正弦稳态电路，这些有特殊条件的电路，由全部电源共同作用产生的平均功率、平均储能、平均作用力等，满足叠加性。

(2)满足特殊条件的二端口网络，它吸收的总平均功率满足叠加性。

(3)在平均功率满足叠加性的特例中，并不意味着平均功率与激励电压或电流之间是线性关系。在所举出的例子中，功率、能量、作用力等，与激励电压或电流之间都不满足齐次关系，因而都是非线性关系。

(4)本文讨论的功率叠加性进一步表明，某些非线性问题仍然可以使用叠加定理来分析，叠加定理与线性系统数学意义上的可加性是有别的。