顾及恶劣海况的船舶救援路径规划

马凯强, 任利锋, 曾 喆, 万剑华

顾及恶劣海况的船舶救援路径规划

马凯强1, 任利锋2, 曾 喆1, 万剑华1

(1. 中国石油大学(华东) 海洋与空间信息学院, 山东 青岛 266580; 2. 中国石油集团东方地球物理勘探有限责任公司海洋物探分公司, 天津 300457)

为了保障救援船舶在恶劣海况环境下能够安全、高效地到达救援区域, 本文改进人工鱼群算法开展海上救援路径规划研究。选取地形、海风和海浪等指标进行风险度量, 采用GIS(geographical infor­mation system)多指标决策方法构建海洋环境威胁场, 通过粒子群算法计算救援路径规划的最佳参数, 并实现海上救援路径搜索。实验表明, 基于改进的人工鱼群算法规划的船舶救援路径效果更优, 可为海上应急救援提供辅助决策参考。

恶劣海况; 路径规划; 人工鱼群算法

近年来, 随着海上贸易的日益繁荣, 海上安全事故频频发生。为了减少船舶人员和财产的损失, 人们对于海上突发事件的应急救援提出了很高的要求。在恶劣海况环境下, 风、浪等自然环境复杂多变, 具有较大的不可预测性, 船舶航行的风险仍然很高[1]。因此, 研究恶劣海况环境下的船舶救援路径规划方法对海上应急救援具有重要意义。

路径规划研究除了Dijkstra算法、人工势场法和A*算法等传统方法[2-3]外, 还包括蚁群算法、粒子群算法、遗传算法等群智能算法[4-5]。由于群智能算法具有搜索效率高、全局搜索能力强和适用于各种复杂环境等特点, 其已成为了当今研究的热点。王沛栋等[6]利用蚁群算法实现了机器人在静态环境下的路径规划。向祖权等[7]利用粒子群算法实现了无人船规避障碍物的最优路径规划。范云生等[8]利用栅格法对电子海图建立海洋环境, 提出一种改进遗传算法的全局路径规划算法。人工鱼群算法是一种简单易实现、鲁棒性强和全局优化能力强的群智能算法, 已应用于船舶的路径规划领域[9]。

目前船舶路径规划研究中海洋环境建模大多只考虑了地形静态环境因素, 较少考虑风、浪等气象水文环境因素。余梦珺等[10]在西北航道上构建了基于海冰密集度、海表温度、风强度的海上环境威胁场, 利用蚁群算法进行了海上救援路径规划研究, 但其只适应于西北航道区域, 未能解决在恶劣海况等其他情况下的救援路径规划。鉴于此, 本文将改进人工鱼群算法应用于恶劣海况环境下, 实现了顾及地形、海风和海浪等指标的船舶救援路径规划。

1 救援路径规划模型的建立

本文研究内容主要包括3部分: 确定规划目标, 构建海洋环境威胁场, 海上救援路径规划。本文以恶劣海况环境下路径最短、风险最小作为规划目标, 采用GIS多指标决策方法构建海洋环境威胁场, 利用改进人工鱼群算法规划海上救援路径, 综合考虑安全性和高效性。规划模型流程图如图1所示。

1.1 研究区域和规划目标

1.1.1 研究区域

本文选取辽东半岛附近海域为研究区域: 经度为120.5°～123.5°E, 纬度为38.26°～39.66°N。

1.1.2 规划目标

海上救援路径规划实质上指救援船舶从起点出发, 在保证自身安全的情况下, 以最短的时间到达事故区域进行救援。假设船舶全程匀速行驶, 航行时间就可用路径长度来代替。路径长度可表示为:

图1 顾及恶劣海况的船舶救援路径规划流程图

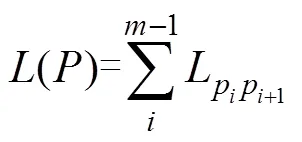
船舶的航行安全可用路径的风险代价来表示。风险代价可表示为:

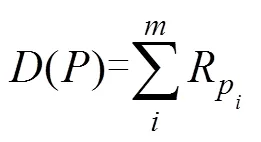
因此, 救援路径规划的总目标函数可由路径长度和风险代价加权计算, 表示为:

()=1×() +2×(), (3)

式中,()为总目标值,1、2为比例系数, 其大小由决策者根据情况进行调整, 本文设1=0.4,2=0.6。

1.2 构建海洋环境威胁场

1.2.1 确定海洋环境风险因素

与陆地不同, 海洋环境非常复杂。海洋地理环境常分为两类: 一类是包含水深、陆地、岛礁及浅滩等静态地形环境; 另一类是包含海风、海浪等动态气象水文环境。在恶劣海况下, 大风和大浪是影响船舶航行的重要因素。大风可直接影响船舶的航行方向, 可能造成碰撞等事故。大浪可对船舶有纵向、横向、垂向的影响, 可能会造成螺旋桨、仪器损坏[11]。地形因素也是船舶航行安全的重要危险因素。在水深较浅、海岸和岛礁附近海域, 浅滩、礁石等航行障碍物较多, 船舶极易发生碰撞、搁浅等事故。另外, 海流也是影响船舶航行的因素, 但在恶劣海况环境中, 表层海流主要受海风影响, 其对船舶的危险度可通过海风和海浪的作用来表示, 因此可忽略。根据以上原因, 本文选取了地形、海风、海浪3个风险因素, 分别对其进行量化评价。

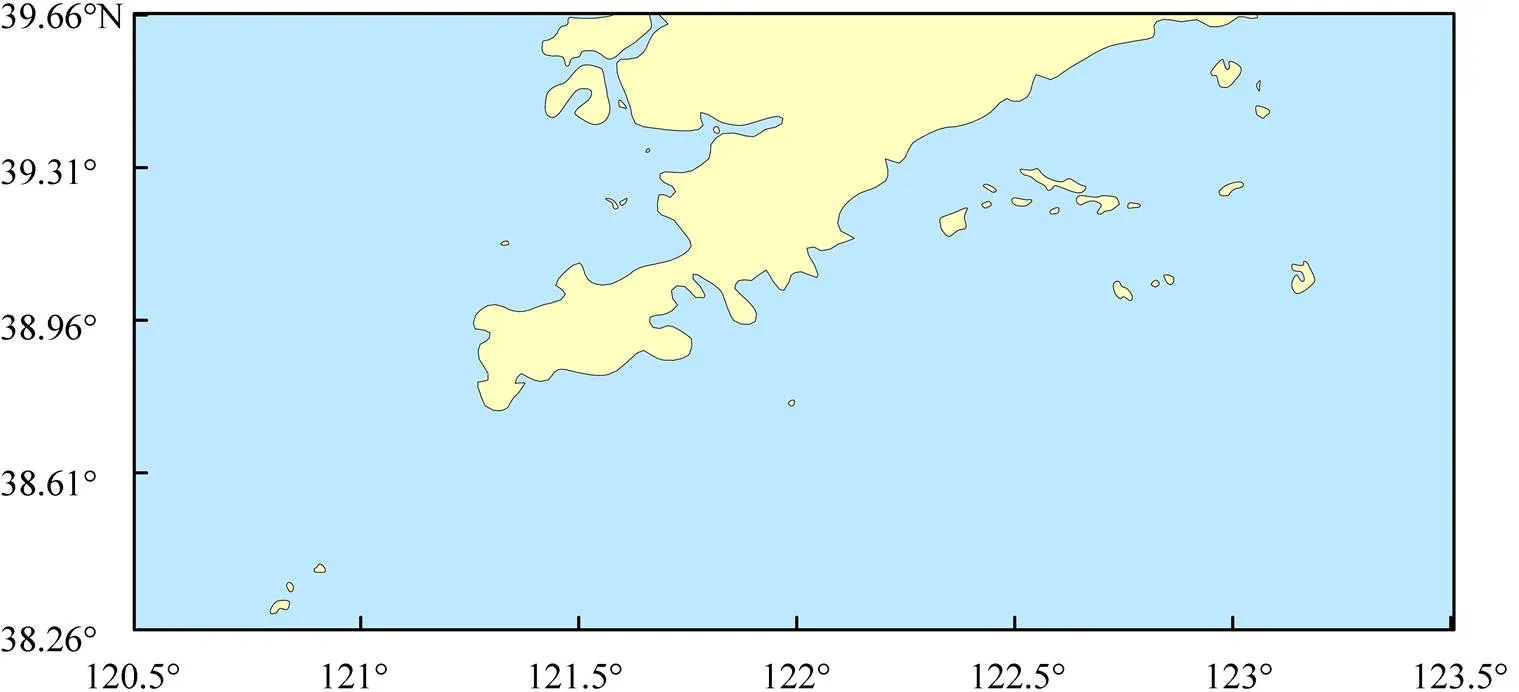
图2 研究区域

(1) 风强度

风强度的大小是用风速来表示的, 风速越大, 风强度也越大。风强度1的量化公式为:

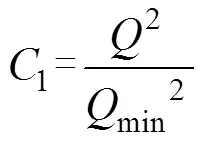
式中,为单个栅格单元的实际风速值,min为大风最低危险值, 根据蒲福风力等级表,min定为17.1 m/s。

(2) 浪强度

浪强度的大小是用浪高来表示的, 海浪越高, 浪强度也越大。浪强度2的量化公式为:

式中,为单个栅格单元的实际浪高,min为海浪最低危险值, 根据海况等级表,min定为4.5 m。

(3) 地形危险度

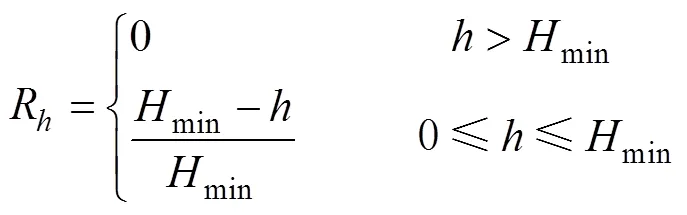
式中,为单个栅格单元的实际水深,min为船舶的最小安全水深, 为了满足大部分救援船舶的航行安全,min确定为15 m。

离岸距离危险度R的量化公式:

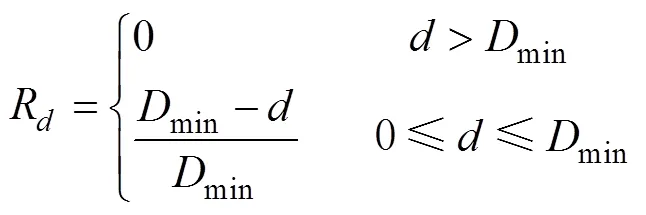
式中,为单个栅格单元距离海岸线的距离,min为船舶的最小离岸距离, 其值定为12 n mile。

地形危险度的量化公式:

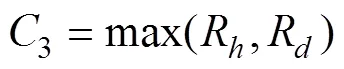
式中, 地形危险度3是取单个栅格单元中水深危险度与离岸距离危险度的最大值。

水深地形数据来自美国地球物理中心(national geophysical data center, NGDC), 海风、海浪数据来自欧洲中期天气预报中心(Europen center for medium- range weather forecasts, ECMWF)。本文选取2019年10月14号14时(UTC)的数据, 此时研究区域最大浪高达4.5 m以上, 符合2万吨以下船舶恶劣海况的标准[12]。由于各个指标的数据都是网格数据且数据间存在分辨率不一致等问题, 需要对各因素进行空间分析处理, 统一为栅格大小为0.02°× 0.02°的栅格图。各个指标使用的空间分析方法如表1所示。

表1 各指标的空间分析方法

1.2.2 海洋环境威胁场建立

GIS多指标决策方法是一种综合评价地理空间的方法。OWA(order weighted average)是根据数据的排序位置进行加权聚合的算子。GIS-OWA方法是GIS多指标决策方法中能根据决策者偏好来评价风险大小的方法, 该方法能从指标补偿差异等方面提高决策者对结果的满意度[13]。基于GIS-OWA的海洋环境威胁场构建主要有3个步骤: 计算指标权重、计算次序权重和OWA算子合并。

指标权重是由层次分析法来确定的。层次分析法用专家的经验判断各风险因素之间的相对重要程度, 并合理地给出每个风险因素的指标权重。

次序权重可由指标的重要程度来确定。次序权重v可定义为:

OWA算子合并可由指标权重和次序权重计算得出。OWA算子的表达式为:

经过5名专家打分后, 由层次分析法可计算出浪强度、风强度、地形危险度的指标权重值分别为0.426, 0.412, 0.162。设=0.6, 由公式(9)可计算出浪强度、风强度、地形危险度的次序权重分别为0.659 8, 0.236 6, 0.103 6。最后, 以公式(10)的OWA算子进行空间计算可得到海洋环境威胁场。如图3, 在海洋环境威胁场中, 西部海域风险低, 东部海域风险高, 东北岛礁附近的海域风险最高, 东南海域风险较高。

1.3 海上救援路径规划算法

人工鱼群算法是由李晓磊等[14]提出的一种群智能优化算法。鱼群在水中寻找食物时, 往往会自行或尾随其他鱼找到食物浓度多的位置。通过鱼群觅食的这个特点, 人工鱼可模拟鱼群的觅食、聚群和追尾行为, 找到一条从起点到终点的最佳路径。

本文针对传统人工鱼群算法易陷入局部最优和路径冗长的问题。对算法进行了以下的改进。

图3 海洋环境威胁场

Fig. 3 Marine environment threat field

1.3.1 人工鱼游走方式改进

传统人工鱼群算法的人工鱼游走方式是随机搜索, 改进方法是采用混沌搜索。混沌搜索具有随机性、规律性、遍历性等特点。因此, 混沌搜索比随机搜索更优越[15]。混沌搜索可表示为:

式中,x是0到1之间的一个随机数。

人工鱼的游走方式也改为:

式中,X()为人工鱼当前的状态,()为人工鱼搜索的状态,X+1()为人工鱼移动一步后的新状态,为人工鱼数目。

1.3.2 视野的改进

传统人工鱼群算法中人工鱼的视野范围是一个定值。视野的大小对算法收敛有较大影响, 视野范围较小时, 执行觅食和随机的行为较多。视野较大时, 执行追尾和聚群的行为较多, 但算法复杂度也变大。因此, 在算法初期, 人工鱼应在较大的视野中寻优, 在算法的后期, 应相应减少人工鱼的视野, 加快算法的收敛速度。视野改进公式为:

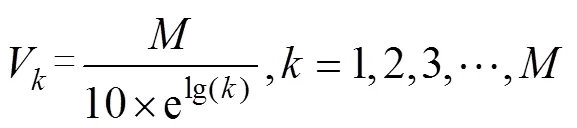
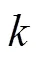
1.3.3 路径冗长的改进

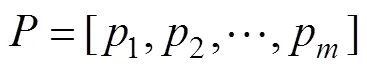
采用以上改进策略, 海上救援路径规划的步骤如下:

①初始化各个参数, 包括人工鱼数目, 最大迭代次数, 拥挤度因子和重复次数。

②采用公式(1)(2)(3)计算每条人工鱼初始的总目标值, 并将其最小值放入公告牌。

③采用公式(13)的结果来作为人工鱼的新视野。

④执行人工鱼的追尾、聚群和觅食行为, 并采用行为选择策略选择最优的前进方向, 同时更新每条人工鱼的位置。

⑤每条人工鱼执行各种行为后, 计算每条人工鱼的总目标值, 取其最小值与公告板的值比较, 若小于时, 更新其值作为公告板的值。

⑥判断是否满足终止条件, 若满足, 执行步骤⑦, 否则, 跳转到步骤③。

⑦将路径进行平滑优化, 输出公告板中的值和对应的路径, 即为最优路径。

2 实验

2.1 海上救援路径规划算法参数优化

人工鱼群算法的参数选择不合理会导致算法运行效率变低或易陷入局部最优。因此, 需要对算法的主要参数进行优化。人工鱼群算法有5个基本参数: 人工鱼数目、视野、步长、拥挤度因子和重复次数。由于栅格网的限制, 人工鱼只能以相邻的栅格作为步长。因此, 本文需要在除步长外的其他4个参数中寻找最优参数。这4个参数对人工鱼群算法性能的影响如下[16]:

1) 人工鱼数目是算法的重要参数。人工鱼数目越多, 跳出局部最优解的能力也越强, 收敛速度也越快。相应地, 数目越多, 效率就会变低。因此, 人工鱼数目要在满足稳定收敛下, 选取较少的人工鱼数目。

2) 视野对算法中各种行为的选取有较大的影响。由式(13), 人工鱼视野范围的大小取决于迭代次数的大小。

3) 尝试次数对人工鱼算法的影响表现在其越大, 觅食能力越强, 收敛效率越高。

4) 拥挤度因子对人工鱼算法的影响表现在其可避免人工鱼由于过度拥挤而陷入局部最优解。

本文采用粒子群算法对人工鱼群算法参数进行优化。粒子群算法的适应值评价函数从算法的寻优能力、收敛速度和运算时间3方面考虑[17]。适应值函数如下:

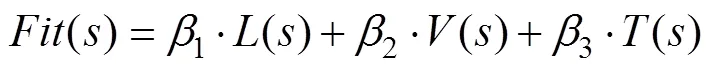
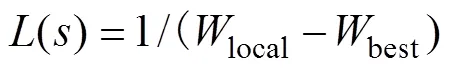
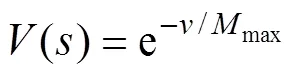
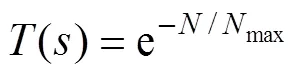
式中,()为粒子群算法的适应值,1,2,3为比例值, 分别为0.5, 0.25, 0.25。()表示人工鱼群算法的寻优能力,local表示人工鱼群算法得到的最优解,best为理论最优解。()表示人工鱼群算法的收敛速度,是鱼群找到最优解时的迭代次数,max为鱼群算法迭代次数的最大值, 取为500。()表示鱼群算法的运行时间,max为鱼群数目的最大值, 取为50。

粒子群算法采用基本算法, 其参数粒子个数为10, 学习因子1=2= 0.5, 惯性因子= 0.5(–)/+ 0.4,迭代次数为100,为当前迭代次数。人工鱼群算法的参数取值范围如表2所示。

表2 人工鱼群算法参数取值范围

图4是粒子群算法迭代过程中适应值的变化曲线。图4显示, 适应值总体上一直呈上升趋势, 表明参数一直在向全局最优的方向趋近。求得的参数可作为海上救援路径规划算法的最佳参数, 最佳参数为:=32,=212,=0.628,=8。

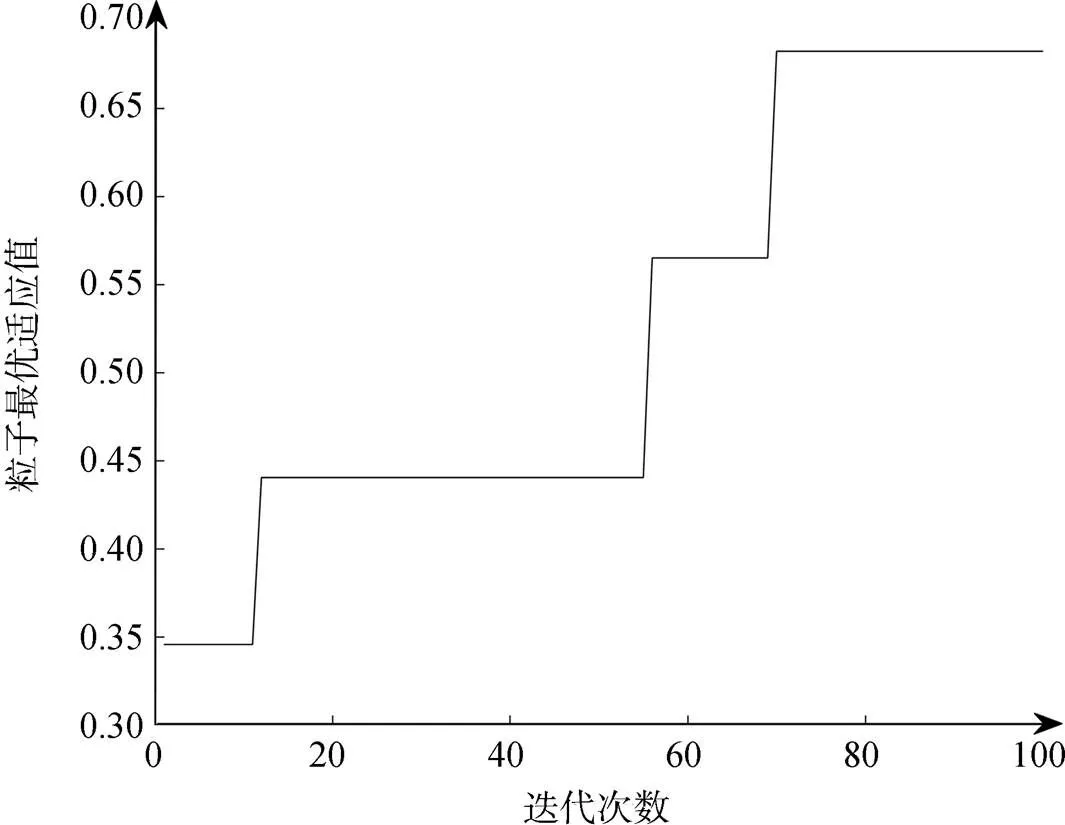
图4 粒子适应值变化曲线

2.2 对比实验

为了验证改进人工鱼群算法能适用于恶劣海况环境下的海上救援路径规划。本文从改进人工鱼群算法的性能和路径上进行分析。设置起点为(120.7°E, 38.52°N), 终点为(122.8°E, 38.46°N)。

根据上述实验得到的最佳参数, 检测阈值设为4, 运行改进人工鱼群算法20次, 记录其每次的优化结果。采用与改进人工鱼群算法相同的参数, 视野为10, 运行传统人工鱼群算法20次, 也记录每次的优化结果。表3给出了改进人工鱼群算法和传统人工鱼群算法各运行20次后的结果。从表3可知, 改进人工鱼群算法在最优总目标值、总目标值均值、总目标值方差和平均迭代次数上均优于传统人工鱼群算法, 表明改进人工鱼群算法在寻优能力、稳定性和收敛速度方面均优于传统人工鱼群算法。

表3 改进前与改进后算法性能对比实验结果

从两组实验中挑选出总目标值最优的两条路径进行分析。表4为传统人工鱼群和改进人工鱼群算法的路径对比实验结果。由表4可知, 改进人工鱼群算法在总目标值、路径长度、风险代价上均优于传统人工鱼群算法, 改进人工鱼群算法规划的救援路径能以更短的路径长度和更小的风险到达终点。将路径等距离划分, 可分为前中后三段。由图5中可知, 传统人工鱼群算法得到的路径易陷入局部最优, 路径迂回曲折, 路径的中段部分路段未能绕开较高风险区域, 不符合船舶的实际航行要求。而改进人工鱼群算法搜索的路径更加平滑, 路径的中段一直处于低风险区域, 能很好地避开较高风险区域, 能保障救援船舶安全航行, 更符合船舶的实际航行要求。

表4 改进前与改进后路径对比实验结果

图5 两条路径规划对比图

为了验证以上实验结果的可行性, 选用以上实验中相同的参数, 更换起点和终点, 设置起点为(122.82°E, 39.26°N), 终点为(123.02°E, 38.46°N), 再次进行一组对比实验。从表5中可知, 改进人工鱼群算法规划的救援路径仍能以更短的路程和更小的风险到达终点。从图6中可知, 起终点位于高风险区域的南北两侧, 两条路径均能避开东部岛屿附近风险度接近1的高风险区域。传统人工鱼群算法得到的路径仍会陷入局部最优, 且路径的前段靠近岛屿, 未能保障船舶的安全性。而改进人工鱼群算法规划的路径能从两个岛屿区域中间相对风险较小的区域穿过, 且路径平滑, 表明了改进人工鱼群算法规划的路径的有效性。

表5 改进前与改进后路径对比实验结果

3 结论

针对在恶劣海况环境下救援船舶路径规划问题, 本文提出了基于改进的人工鱼群算法的船舶救援路径规划方法。本文的海上救援路径规划方法搜索到的路径在总目标值、路径长度、风险代价上均优于传统人工鱼群算法, 且路径更加平滑, 能顺利避开海岸、岛礁和高风险区域, 能更好地保障救援船舶安全、高效地到达事故区域。

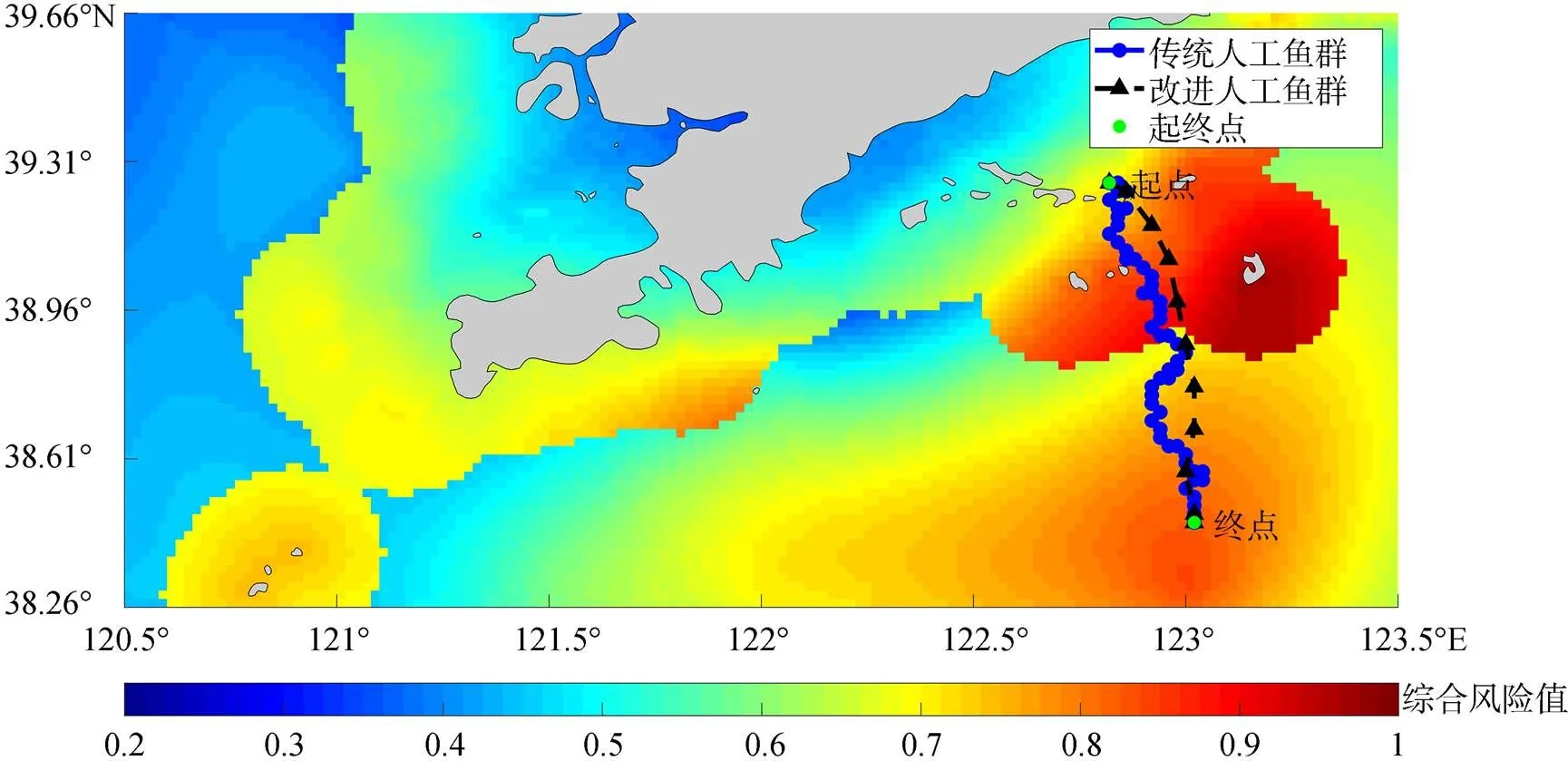
图6 两条路径规划对比图

本研究的不足之处是只考虑了在恶劣海况环境下的部分因素, 且未考虑风向、浪向等对船舶航行效率的影响, 未来将开展更深入的研究。

[1] 戴冉, 郝庆龙, 顾祖旭. 恶劣海况中军用舰船航行决策模型[J]. 中国航海, 2014, 37(3): 68-71, 79.

DAI Ran, HAO Qinglong, GU Zuxu. Sailing Decision Model of Military Vessels on Rough Sea[J]. Navigation of China, 2014, 37(3): 68-71, 79.

[2] CHEN Y B, LUO G C, MEI Y S, et al. UAV path planning using artificial potential field method updated by optimal control theory[J]. International Journal of System Science, 2016, 47(6): 1407-1420.

[3] TOPAJ A G, TAROVIK O V, BAKHAREV A A, et al. Optimal ice routing of a ship with icebreaker assistance[J]. Applied Ocean Research, 2019, 86: 177-187.

[4] TAN Guanzheng, LIU Guanjun. Global optimal path planning for mobile robots based on particle swarm optimization[J]. Application Research of Computers, 2007, 24(11): 210-212.

[5] LI Wei, WANG Gaiyun. Application of improved PSO in mobile robotic path planning[C]//Proceedings 2010 International Conference on Intelligent Computing and Integrated Systems. Guilin: IEEE Network, 2010, 4(4): 45-48.

[6] 王沛栋, 冯祖洪, 孙志长. 一种栅格模型下机器人路径规划的改进蚁群算法[J]. 计算机应用, 2008, 28(11): 2877-2880.

WANG Peidong, FENG Zuhong, SUN Zhichang. Improved ant colony algorithm in grid model for mobile robot path planning[J]. Journal of Computer Application, 2008, 28(11): 2877-2880.

[7] 向祖权, 靳超, 杜开君, 等. 基于粒子群优化算法的水面无人艇分层局部路径规划[J]. 武汉理工大学学报, 2015, 37(7): 38-45.

XIANG Zuquan, JIN Chao, DU Kaijun, et al. Local obstacle avoidance for unmanned surface vehicle using a hierarchical strategy based on particle swarm optimization[J]. Journal of Wuhan University of Technology, 2015, 37(7): 38-45.

[8] 范云生, 赵永生, 石林龙, 等. 基于电子海图栅格化的无人水面艇全局路径规划[J]. 中国航海, 2017, 40(1): 47-52.

FAN Yunsheng, ZHAO Yongsheng, SHI Linlong, et al. Global path planning for unmanned surface vehicle based on grid model of electronic chart[J]. Navigation of China, 2017, 40(1): 47-52.

[9] 马文耀, 吴兆麟, 杨家轩, 等. 人工鱼群算法的避碰路径规划决策支持[J]. 中国航海, 2014, 37(3): 63-67.

MA Wenyao, WU Zhaolin, YANG Jiaxuan, et al. Decision support from artificial fish swarm algorithm for ship collision avoidance route planning[J]. Navigation of China, 2014, 37(3): 63-67.

[10] 余梦珺, 张韧, 高顶, 等. 基于蚁群算法的西北航道海上救援路径规划[J]. 海洋预报, 2019, 36(6): 62-72.

YU Mengjun, ZHANG Ren, GAO Ding, et al. Route planning for maritime rescue in Arctic Northwest Passage based on ant colony algorithm[J]. Marine Forecasts, 2019, 36(6): 62-72.

[11] 解以扬, 刘大刚, 吴丹朱, 等. 黄、渤海恶劣天气影响船舶安全的风险预估技术初探[J]. 灾害学, 2014(1): 136-143.

XIE Yiyang, LIU Dagang, WU Danzhu, et al. Risk prediction technology of ship safety in the Yellow Sea and Bohai Sea during severe weathers[J]. Journal of Catastrophology, 2014, (1): 136-143.

[12] 刘冰, 傅敏辉, 薛国虎, 等. 航天测量船海上测控任务分析与设计方法[M]. 北京: 国防工业出版社, 2015: 194-195.

LIU Bing, FU Minhui, XUE Guohu, et al. Analysis and design method of TT & C mission for space survey ship at sea[M]. Beijing: National Defense Industry Press, 2015: 194-195.

[13] WANG Jiasheng, LI Manchun, LIU Yongxue, et al. Safety assessment of shipping routes in the South China Sea based on the fuzzy analytic hierarchy process[J]. Safety Science, 2014, 62: 46-57.

[14] 李晓磊, 薛云灿, 路飞, 等. 基于人工鱼群算法的参数估计方法[J]. 山东大学学报(工学版), 2004, 34(3): 84-87.

LI Xiaolei, XUE Yuncan, LU Fei, et al. Parameter estimation method based-on artificial fish school algorithm[J]. Journal of Shandong University(Engineering Science), 2004, 34(3): 84-87.

[15] 黄长强, 赵克新. 基于改进蚁狮算法的无人机三维航迹规划[J]. 电子与信息学报, 2018, 40(7): 1532-1538.

HUANG Changqiang, ZHAO Kexin. Three dimensional path planning of UAV with improved ant lion optimizer[J]. Journal of Electronics & Information Technology, 2018, 40(7): 1532-1538.

[16] 王联国, 施秋红. 人工鱼群算法的参数分析[J]. 计算机工程, 2010, 36(24): 169-171.

WANG Lianguo, SHI Qiuhong. Parameters analysis of artificial fish swarm algorithm[J]. Computer Engineering, 2010, 36(24): 169-171.

[17] 刘利强, 戴运桃, 王丽华. 蚁群算法参数优化[J]. 计算机工程, 2008, 34(11): 208-210.

LIU Liqiang, DAI Yuntao, WANG Lihua. Ant colony algorithm parameters optimization[J]. Computer Engineering, 2008, 34(11): 208-210.

Ship rescue path planning considering adverse sea conditions

MA Kai-qiang1, REN Li-feng2, ZENG Zhe1, WAN Jian-hua1

(1. College of Oceanography and Space Informatics, China University of Petroleum, Qingdao 266580, China; 2. BGP INC, China National Petroleum Corporation, Tianjin 300457, China)

To ensure that the rescue ships can reach the rescue area safely and efficiently under adverse sea conditions, this study aims to improve the artificial fish swarm algorithm for maritime rescue path planning. The terrain, sea breeze, and sea wave are selected to measure the risk. The multi-index decision-making method of the geographic information system is used to construct the marine environment threat field. The optimal parameters of rescue path planning are calculated using the particle swarm optimization algorithm, and maritime rescue path planning is realized. The experimental results show that ship rescue path planning based on the improved artificial fish swarm algorithm is effective and can provide auxiliary decision-making reference for maritime emergency rescue.

bad sea; path planning; artificial fish swarm algorithm

Nov. 8, 2020

K928.44; U676.8

A

1000-3096(2021)05-0039-08

10.11759/hykx20201108007

2020-11-08;

2020-12-24

国家重点研发计划项目(2017YFC1405600); 国家自然科学基金项目(41976184)

[National Key Research and Development Program of China, No. 2017YFC1405600; National Natural Science Foundation of China, No. 41976184]

马凯强(1996－), 男, 山西吕梁人, 硕士研究生, 研究方向: 船舶路径规划, E-mail: 1045783321@qq.com; 万剑华(1966－),通信作者, 教授, 主要从事海洋遥感和地理信息方面研究, E-mail: wjh66310@163.com

(本文编辑: 丛培秀)