基于多分类相关向量机的导弹发控电路故障诊断∗

范庚 汉田 马羚

（海军航空大学青岛校区 青岛 266000）

1 引言

导弹发控电路是机载导弹发控系统的重要组成部分。导弹发控电路是一个复杂的数模混合电路，故障模式复杂，故障诊断困难。据统计，对于复杂的数模混合电路，元件级故障中有超过80%的故障出现于模拟电路［1］。由于模拟电路具有复杂的输入-输出关系，电路中的非线性元件多，元件参数与电路响应大多表现为非线性映射关系，因此工程应用中难以精确描述电路响应的数学模型，基于模型的方法无法适用。文献［2］构建了BP神经网络模型用以实现某型空空导弹发控电路故障诊断。为提高故障诊断模型的预测精度和加快网络训练的收敛速度，文献［3］选取广义回归神经网络建立了模拟电路故障诊断模型。文献［4］建立了小波RBF神经网络故障诊断模型，取得了较好的模拟电路故障诊断效果。但神经网络本质上属于传统统计学范畴，其基础来源于渐进理论，即在具有无穷多的学习样本数目的理想条件下，才可在理论上保证模型的性能；同时，神经网络还具有较慢的收敛速度，易陷入局部极值，且隐层数、隐节点数等网络结构难以确定。

相关向量机［5］（Relevance Vector Machine，RVM）是一种基于稀疏贝叶斯理论的统计学习方法，由美国学者Tipping提出，具有参数设置简单、概率式输出等优点［6］。但传统的RVM只能解决二分类问题，在解决多类故障诊断问题时，一般先通过“一对多”法［7］、“一对一”法［8］或二叉树法［9～10］将多类故障诊断问题转化为多个二类故障诊断问题，再构造RVM二类分类器，最终获得诊断结果，但存在诊断速度和诊断精度下降、决策树结构难以确定等问题［11］。Psorakis等［12］用 Multinomial probit函数替代了传统RVM的Logistic sigmoid函数，从而把单个模型的二分类故障诊断问题扩展到多分类故障诊断问题，基于传统RVM提出了直接多分类相关向量机（Multiclass Relevance Vector Machine，mRVM），并且能够给出分类结果的后验概率。

本文针对导弹发控电路的故障诊断问题，提出了一种基于mRVM的方法。首先，建立mRVM模型反映故障特征和故障模式的非线性关系；然后，以交叉验证误差最小为目标函数，采用人工鱼群优化算法自适应选择模型参数；最后，通过仿真实例对方法的性能加以验证。

2 mRVM算法原理

2.1 mRVM模型

式（1）表示新样本属于类别i的概率值，通过更新迭代搜寻最大概率就可确定新样本所属的类别

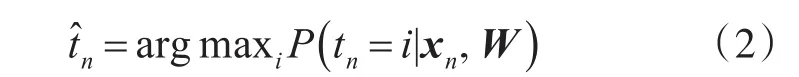
根据贝叶斯框架，为保持模型稀疏，假定权重参数W 中的元素wc服从0均值正态分布，即。其中超参数αcn为尺度矩阵A∈RC×N中的元素，并假定其服从超参数为γ、ν的伽马分布。当γ、ν取较小值时，权重参数W 经过训练后被约束在零值附近，W只有极少数非零的相关向量（Relevance Vectors，RV），由此即可获得稀疏模型。

釆用多层贝叶斯结构的RVM模型如图1所示，其中W是训练模型待求解的变量，A、Y是求解过程的中间变量。基于引入的辅助变量Y，本文在求解参数过程中采用期望最大化（Expectation Maximization，EM）算法。

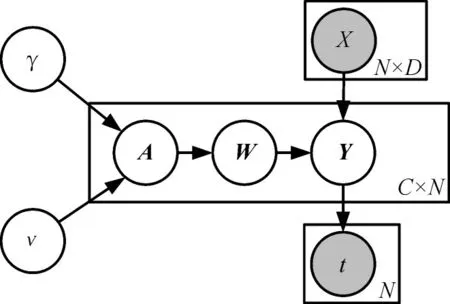
图1 mRVM模型结构示意图

2.2 mRVM的训练

mRVM的模型训练是二型最大似然过程，其样本训练过程中不断更新迭代待求参数的数值。根据每一步迭代更新得到的A值，通过EM算法获得参数W 、Y的更新值，其中用M步估计W ，E步估计Y。

其中，C=I+KA-1KT，C∈RN×N。对C 分解可表示

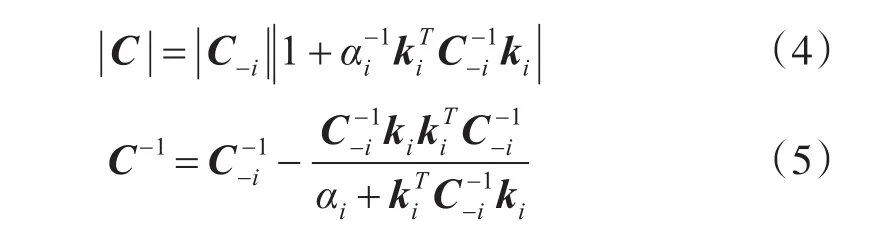
其中，C-i为C隔离样本i的值，αi为样本i对应的超参数，ki为样本i对应的核函数序列。

根据式（4）和（5）可将式（3）进一步表示：

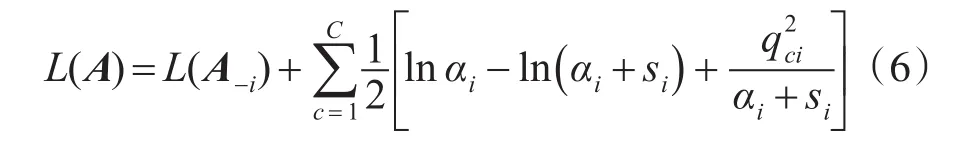
i型已存在特征样本的相似度；，为质量因子，反映了样本ki描述类别的能力。接着求解L(A) 关于 αi的偏微分，使 ∂L(A)/∂αi=0 ，得到驻点：

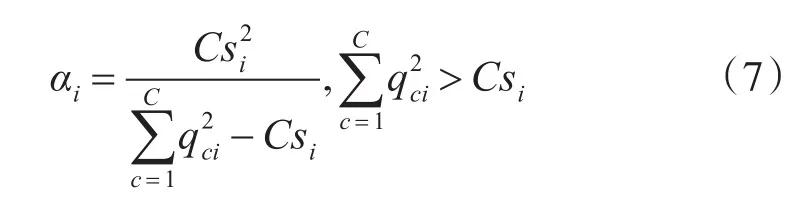
若θi＞0，表明样本i对模型分类有贡献，则根据式（7）更新 αi；

若θi＜0，表明样本i为冗余样本，则设置超参数αi=∞，将其从样本空间剔除。

训练开始随机选择一个样本作为初始样本，将si、qci带入式（7），并假定 C=I，可得到超参数 αi的初始值为

依照上述方法对尺度矩阵A更新后得到A*，A*∈RM×M，其中符号*表示样本训练过程中当前样本数为M时的参数（M≪N）。接着采用EM算法更新权重参数W的最大后验估计值：

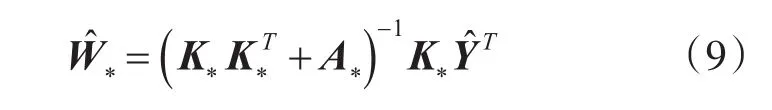
其中，K*∈RM×N，为E步中隐变量Y期望的估计值。

最后根据M步W的估计值，给出E步中辅助变量Y的期望的更新值。辅助变量Y为C×N维锥形截断高斯分布，第i类样本的辅助变量 yin期望的估计值 ŷin由式（10）更新，同时辅助变量 ycn期望的估计值 ŷcn由式（11）更新：

基于mRVM的训练过程即为参数W、A、Y的更新迭代过程。当所有满足θi＞0的样本均包含在样本空间，所有θi＜0的样本均剔除样本空间，且相邻两步迭代中尺度矩阵A的取值满足（ε通常取10-12），则判定模型收敛，迭代结束。

综上所述，mRVM的迭代流程如下。

步骤1根据目标值t初始化辅助变量Y，令所有样本的超参数初始值均为αi=∞，再随机选择一个样本i并根据式（8）为其超参数αi赋初始值；

步骤2若尚未满足收敛条件，则执行迭代过程。首先，更新尺度矩阵参数 A*，计算样本的θi和 αi：

1）若 θi＞0 且 αi＜∞ ，则根据式（7）更新 αi，保留特征样本；

2）若 θi＞0且 αi=∞ ，则根据式（7）设置 αi，添加特征样本；

3）若 θi≤0且 αi＜∞ ，则令 αi=∞ ，提出特征样本。

步骤3M 步：根据式（9）更新Ŵ*；

步骤4E 步：根据式（10）、（11）更新Ŷ；

步骤5比较所有特征样本和非特征样本的θi参数值，确定下一个样本，重复步骤2～步骤4，当满足收敛条件时，训练结束。

2.3 模型参数优化

选择Gauss核函数作为模型核函数

其中为γ核参数。

核参数对模型性能有较大影响，随机设置可能会产生较大的诊断误差。

留一交叉验证的基本原理为假设当前训练样本集由N个样本组成，每次训练过程任选一个样本作为测试集，其他N-1个样本用于训练并测试模型。依次选取不同样本作为测试集，重复N次训练过程，最终获得每个样本作为测试集的测试误差，则定义留一交叉验证误差为所有测试误差的平均值。显然，mRVM模型的泛化能力可由留一交叉验证误差的大小直接反映。为避免穷举法导致计算时间过长问题并实现模型参数选择的自适应优化，本文采用鱼群算法［9］设置核参数。鱼群算法能够有效避免优化结果陷入局部极值，而最终得到全局最优解，并同时兼顾较快的收敛速度。具体实现过程如下。

步骤1初始化鱼群：假设初始状态的迭代次数g=1，鱼群大小为H，每条人工鱼的初始位置pi在核函数γ的取值范围内随机生成，i=1，2，…，H，最大迭代次数为Nmax。同时设定人工鱼单步移动的最大步长为λ，感知距离为V，拥挤度因子为δ，每条人工鱼最多可实施觅食行为Ntry次。

步骤2觅食行为：食物浓度函数设定为留一交叉验证误差的目标函数。已知当前人工鱼处于pi的位置，对应的食物浓度为ci，在人工鱼的感知距离内任意选择一个位置pj，所对应的食物浓度为cj。如果食物浓度满足ci＜cj，则人工鱼向位置pj方向移动一步，实施觅食行为；否则，重新选取一个位置pj，再次判断食物浓度关系是否达到移动条件，若条件仍旧无法满足则再次选取新的位置，当觅食行为次数达到上限Ntry时停止移动。如果此时移动条件仍无法得到满足，那么可执行随机操作，即在人工鱼的感知距离V内向任意方向移动一步。

步骤3聚群行为：假设当前人工鱼位于pi的位置，所对应的食物浓度为ci。在人工鱼的感知距离内发现数量为nf的人工鱼群，经探测可得到鱼群的中心位置为pc，所对应的食物浓度为cc。计算中心位置的平均食物浓度，若满足ccnf＞δci，表明中心位置的拥挤度较低且食物较多，人工鱼则可向中心位置pc方向移动一步；否则执行觅食行为。

步骤4追尾行为：假设人工鱼当前位于pi的位置，对应的食物浓度为ci。在人工鱼的感知距离内搜索到最大食物浓度为cmax，对应的位置为pmax。设在感知距离内以pmax为中心可搜索到人工鱼数目为nf，如果位置pmax处的平均食物浓度满足关系，表明该位置拥挤度较低且食物较多，人工鱼则可向pmax方向移动一步；否则返回执行步骤2。

3 实例仿真与分析

3.1 仿真说明

仿真环境：Intel Core i5-7500 CPU，8GB DDR内存，Windows 7操作系统，实验中所涉及算法均采用MATLAB软件编程并调试运行。运用PSpice中的OrCAD Capture模块搭建某型空空导弹的部分发控电路，电路原理如图2所示。

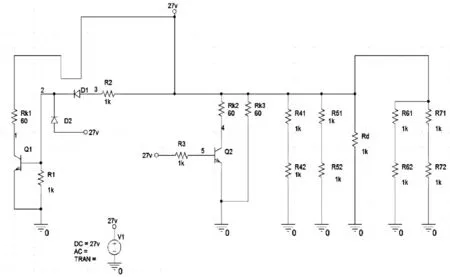
图2 仿真电路图

运用PSpice软件中的probe模块的偏压点分析仿真电路，获取设置测点的电压数据，见表1。表中A0～A4分别代表电路正常、“载机供电”功能电路故障、“发射允许”功能电路故障、“正常发射”功能电路故障和“导弹供电”功能电路故障；t1～t5分别代表1～5点的测试电压值。

表1 故障样本数据

对四个功能电路故障模式及正常模式进行故障类别编码，见表2。

表2 功能电路故障编码

从表1中选择4组样本作为测试样本，如表3所示，剩下的15组样本作为训练样本。

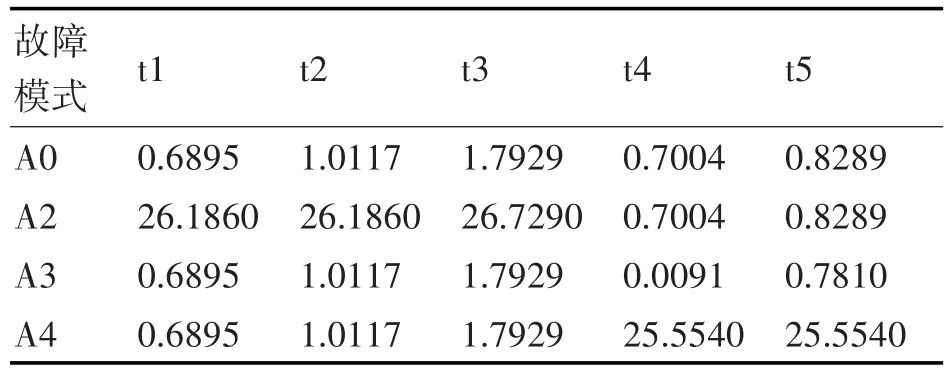
表3 测试样本数据

3.2 模型参数的确定

模型优化过程中设置参数为人工鱼数目设为10，单步移动的最大步长为0.01，最大迭代次数为10，人工鱼可尝试觅食行为的最大次数为10，感知距离为1，并设拥挤度因子为0.618，核参数的取值区间为［0.001，100］。

图3所示为本文所提方法的参数自适应优化迭代过程。由迭代结果表明：只需1次迭代即可得到优化的模型参数，充分验证了该方法的收敛性能指标能够达到预期结果。参数优化结果为γ=13.988。

图3 参数自适应优化迭代过程

3.3 仿真结果与分析

将本文方法（mRVM）与文献［2］的方法（BPNN）进行对比，仿真结果如表4所示。

表4 仿真结果

从仿真结果可以看出，本文方法诊断精度为100%，对测试样本均实现了正确识别；在训练速度和诊断速度方面优于文献［2］的方法。

4 结语

本文针对导弹发控电路的多类故障诊断问题，提出一种基于mRVM的方法。首先，建立mRVM模型反映故障特征和故障模式的非线性关系；然后，以交叉验证误差最小为目标函数，采用鱼群算法自适应选择模型参数；最后，通过仿真实例验证了方法的有效性。仿真结果表明：该方法在保证诊断精度和诊断速度的同时，避免了BP神经网络的结构难以确定、需要大样本训练数据和容易陷入局部极值问题，具有较高的工程实用价值。