Morphologies of a spherical bimodal polyelectrolyte brush induced by polydispersity and solvent selectivity∗

Qing-Hai Hao(郝清海) and Jie Cheng(成洁)

College of Science,Civil Aviation University of China,Tianjin 300300,China

Keywords: surface morphologies;polydisperse polyelectrolyte brush;solvent selectivity;molecular dynamics simulation

1. Introduction

Bimodal polyelectrolyte (PE) brush, composed of two chemically distinct polyions tethered on a planar or curved surface, is an excellent strategy to control and regulate interface interactions, which has many practical applications, such as colloid stability,[1]antifouling surfaces,[2]lubrication,[3]drug delivery,[4]and stimuli-responsive materials.[5–8]It has been demonstrated that polydispersity of immobilized polyions can significantly broaden the range of parameter space for the tailoring of environment-responsive surface properties.[2]Compared to mono-disperse polymer brushes, the surface morphologies of bimodal PE brushes in response to environmental changes have not been well understood in theory or simulation.

Comprehensive understanding of the phase behavior of bimodal PE brushes is crucial for the future development of specific applications. Specifically, the surface morphology of bidisperse polymer brush is governed by a number of factors,such as molecular weights of two tethered chains, selectivity of solvent,grafting densities,as well as curvature of the grafting substrate.[5–8]So far,a series of surface structures in neutral bimodal polymer brushes were identified in theory,[9–14]experiment,[15–18]and simulation.[19–21]Marko and Written were the first to theoretically investigate the microphase separation of symmetric mixed neutral planar brushes under equilibrium melt conditions.[9]Both the lateral(a“rippled”nanostructure) and vertical (a “layered” morphology) phase segregations were predicted. Employing self-consistent field(SCF)theory, Tang and coworkers studied phase structures of uncharged binary mixed homopolymer brushes grafted onto a nanosphere. By adjusting grafting density,composition,chain length asymmetry,and radius of nanosphere,a series of islandlike morphologies with different island numbers characterizing specific structural symmetry were obtained, which were similar to the structures of dense packing of microspheres in small clusters.[10]In their subsequent work,[11]the phase structures of neutral binary mixed homopolymer grafted on the surface of a nanorod,immersed in a nonselective solvent,were studied. Either perpendicular or parallel ripple structure was found for the symmetric bimodal polymer brushes.By a lattice-based SCF approach, the phase separation of binary mixed polymer brushes tethered on cylindrical surface under good solvent conditions was explored by Egorov.[12]The macrophase separation was observed for two immiscible polymers of the same length. However,the microphase separation was promoted by the mismatch of the chain length between two tethered polymers, that is, the ring-shape stripes perpendicular to the cylinder axis. Using the SCF theory,Huret al.calculated a phase diagram of the mixed polymer brush with the same chain length under melt conditions,and the effects of the segregation force and composition were considered.[13]Recently,Qiet al.studied the effect of polydispersity on the structure of neutral planar polymer brushes by means of analytical theory, SCF approach, and Monte Carlo(MC) simulations.[14]The hydro-dynamical shear flow and penetration depth of mixed polymer brushes induced by the polydispersity were also examined.

In contrast to the intriguing phase morphologies for neutral binary mixed polymer brushes predicted by theoretical studies, the overall experimental studies of surface structure of bimodal brush lags behind the theoretical study, which is largely because of the challenge in the synthesis of welldefined polydisperse brushes and in the unequivocal identification of the surface structures.[5]By means of scanning tunneling microscope(STM)imaging,Jacksonet al.reported for the first time that gold and silver nanoparticles coated with mixtures of ligands formed ripple-like structures in their ligand shells, which can be controlled by tuning the molar ratio and the nature of ligands.[15]Using transmission electron microscopy (TEM), Baoet al.firstly conducted a systematic study on lateral microphase separation of mixed poly(tertbutylacrylate) (PtBA)/polystyrene (PS) brushes anchored on silica particles induced by molecular weight.[16]Rossner and co-workers revealed the surface patterns of mixed poly(methyl methacrylate) (PMMA)/PS homopolymer brushes grafted at gold nanoparticles by size-exclusion chromatography (SEC)and MC simulations.[17]The Janus-type structures were observed due to the lateral mobility of grafting points. Very recently, Gopalan’s group fabricated mixed PMMA/PS brushes on the planar substrate and demonstrated experimental validation of the predicted morphologies from uniform to cylinder to ripple structures in melt phase by varying PS chain lengths with fixed PMMA chain length.[18]Their results were supported by the phase diagram established by MC simulations based on a coarse-grained model.

Previous simulation studies have highlighted patterned morphologies of nonionic mixed polymer brushes induced by the environmental parameters.[6,19]For example, Dong and Zhou investigated the responsive behavior of mixed PS/poly(ethylene oxide) (PEO)-modified amphiphilic gold nanoparticles in five different solvents by coarse-graining molecular dynamics(MD)simulations.[20]Typical morphologies, that is, Janus-type, buckle-like, ring-like, jellyfish-like,and octopus-like, were formed by adjusting the distributions of tethered points(even or Janus)and solvent quality. Very recently, Lu and coworkers developed an adsorption-migration reaction model and studied the dynamic evolution process of binary ligands adsorbed on nanoparticle surfaces during adsorption reaction by dissipative particle dynamics (DPD)method.[21]A rich variety of surface morphologies,including Janus,patchy,stripe and island patterns,were predicted by alternating the adsorption reaction and phase separation rates.

In addition to nonionic mixed polymer brushes, polydispersity of grafted polyions could respond to a wider range of external stimuli than the neutral counterpart.[22]However,studies of polydisperse PE brushes are still rare. Zhulina and coworkers addressed the effect of dispersity of charged macromolecules on structural and responsive properties of planar PE brushes by an analytical SCF approach.[23]Only the overall stratification in binary PE brushes was predicted. Polydispersity is an intrinsic characteristic for each of all synthetic polymer brushes due to the great challenge in fabricating monodisperse polymers.[22]Furthermore,brush-like layers of charged macromolecules are found as motifs in natural objects, and many of these layers are highly polydisperse.[24]For example,mucins in periciliary layers in airways and aggrecans in synovial joints consist of the core proteins decorated by polysaccharide chains comprising several isoforms.[25,26]In this work,we investigate the surface morphologies of bidispersed PE brushes end-grafted on a nanocolloid in the presence of trivalent counterions by MD simulations. The focus is on the surface patterns induced by the hydrophilic or hydrophobic properties of solvent and mismatch of chain length of two ligands.Our predictions of the binary spherical PE brushes can serve as a guide for designing and manufacturing next-generation information storage and electronic devices.

2. Model and simulation details

Simulations of spherical bimodal PE brushes are carried out by employing a well-tested coarse-grained model,[27,28]which are implemented in an open-source software LAMMPS.[29]All the physical quantities are dimensionless throughout this paper based on the three fundamental quantities,massm,distanceσ,and energyε. Other units are derived from these basic ones. The bimodal PE brushes are constructed by two strong (quenched) PE chains (refers as A and B)with degrees of polymerizationNAandNBend-grafted on the surface of nanocolloid. The nanocolloid with radiusRis formed by overlapping a certain number of beads with diameter 1.0,which is used to prevent the monomers and counterions from penetrating into the interior of the nanocolloid. Two species of flexible PE chains,where the monomers are simplified to spherical beads connected by elastic springs, are endgrafted evenly on the surface of nanocolloid. Each monomer of the two tethered chains carries a negative unit charge−e,which corresponds to charge fractionf=1.0. The numbers of the two tethered PE chains are chosen asMA=MB=18,which are not varied throughout the simulations. The trivalent counterions are inserted randomly into the simulation box to neutralize the bare charge of the mixed brush. The solvent is treated implicitly and periodic boundary conditions are selected for all directions.

Non-bonded pairwise interaction between any two beads is described by a truncated and standard shifted Lennard–Jones(LJ)potential

whererdenotes the distance between any two particles,εLJis the strength of the pairwise interaction mimicking the depth of the attractive well of the potential,andrcutis the cutoff radius. Specifically,εLJ=0.1kBT(kBis Boltzmann’s constant andTis the absolute temperature),rcut=2.5 is chosen for monomer-monomer interactions, which corresponds to good solvent condition for polymer backbone;εLJ= 1.0kBTandrcut=2.5 represent poor solvent condition of polymer backbone. For other pairewise interactions, the LJ interaction parameters are set asεLJ=1.0kBTandrcut=21/6.Cis a constant,which ensures that the potential energy is continuous at the cutoff distance.

The finite extension nonlinear elastic (FENE) is used to model the bonded interaction between two adjacent monomers,[27,30]which is given by

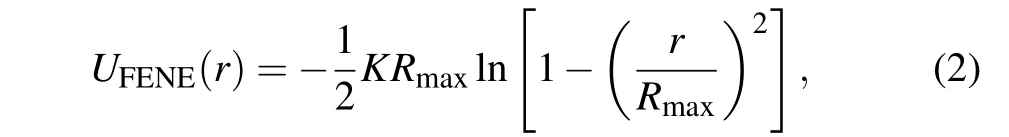
whereK=30kBT/σandRmax=1.5 refer to the spring constant and the maximum bond length,respectively. The attractive FENE potential combined with the excluded volume interaction (LJ potential) can prevent the bonds to penetrate each other and generate an average bond length of 0.97.[31]

Electrostatic interactions between any two charged beads with charge valencesqiandqjare mimicked by the Coulomb potential

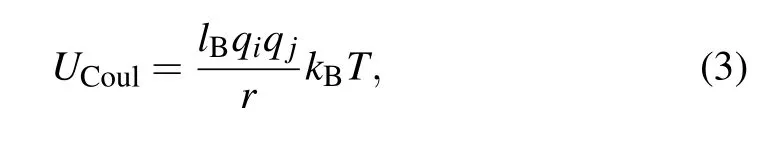
wherelB=e2/ε0εrkBTis the Bjerrum length (ε0andεrare the vacuum permittivity and the relative dielectric constant of the implicit solvent, respectively). Noting thatlBin solutions is about 2∼5 times of distance between charged segments along polymer backbone for many synthetic polyions and biomacromolecules,[32]we choose a standard valuelB=3.0 in our simulations.[33]The particle-particle/particle-mesh(PPPM)algorithm with an estimated accuracy 10−3is used for calculating the long-range part of the Coulomb potential.[34]

Simulations are carried out in the canonical ensemble (i.e.,NVTensemble). The constant temperatureT=1.0ε/kBis maintained by coupling the system to a Langevin thermostat,[29]in which the motions of beads satisfy the Langevin equation:

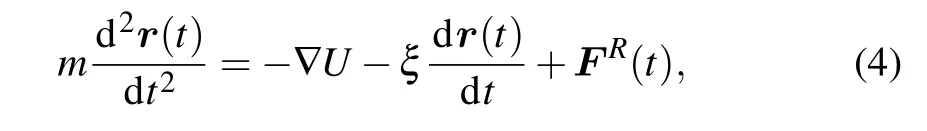
whereU=ULJ+UFENE+UCoulis the total potential of the system;ξandFR(t)are the friction coefficient and the stochastic force of the implicit solvent,respectively. The friction coefficient is set asξ=0.1mτ−1, whereτis the standard LJ timeτ=σ(m/ε)1/2.The stochastic force is assumed to have a zero average value and satisfies the fluctuation-dissipation theorem.The velocity-Verlet algorithm with a time step ∆t=0.005τis employed for integrating the equation of motion.

The dispersity effect of bimodal PE brush is introduced by the mismatch parameter

whereNA= 24 is fixed during our simulations.NB= 24,36,..., 108, which means that the mismatch parameter range is 0.0≤β ≤3.5 in our simulations. Besides the differences of polymerization degree of the two grafted chains, the interaction compatibility between monomers A and B is characterized by the strength of LJ potentialεLJ,which is implemented by defining an effective interaction parameter of A-monomer and B-monomerχAB=(εAA+εBB−2.0εAB)/2.0. Specifically,χAB=0 means that the two tethered PE backbone are chemically identical;εAA=εBB=εAB=0.1kBTandεAA=εBB=εAB=1.0kBTare selected to mimic the good and poor solvent conditions of the bimodal PE brushes,[35,36]which will be referred asχAB=0 & good andχAB=0 & poor, respectively. Furthermore,εAA=εBB=1.0kBTandεAB=0.1kBTyieldingχAB＞0(=0.9)as well asεAA=εBB=0.1kBTandεAB=1.0kBTresultingχAB＜0 (=−0.9) are also investigated to reveal the interaction incompatibility effect on the morphologies of bimodal PE brushes.

Three different radius of nanocolloid are considered,that is,R=3.0, 6.0, 10.0, which corresponds to the grafting densityσg=(MA+MB)/(4πR2)=0.318, 0.080, 0.029, respectively. The side lengths of the cubic simulation box are set asLx=Ly=Lz=240,which are large enough to prevent the binary PE brush from interacting with itself through periodic boundaries.[37]

The simulations are performed in the following procedure. Initially, the nanocolloid is located at the center of the simulations box, which is stationary during the simulation.The tethered binary mixed PE chains in the fully extended configuration stretch along the radial direction. The trivalent counterions are randomly inserted into the simulations box.To eliminate any“memory”of the initial configuration,the bimodal PE brush system is heated up toT=3.0 by rescaling bead velocities for 4×106time steps before our simulation.Then the system is cooled gradually down toT=1.0 lasting 6×106time steps. After the equilibration run taking 6×106steps, another production run lasts 4×106steps. During the production, one configuration is sampled every 2×103steps and 2001 configurations are saved to collect data for analyzing the bimodal PE brushes in our programs.

3. Results and discussion

The relaxation of the spherical bimodal PE brushes can be investigated by monitoring the fluctuations in the brush parameters.Therefore,to identify a steady state is reached in our simulation, we first calculate the autocorrelation functions of radius of gyration of grafted PE chain,which is defined as[38]

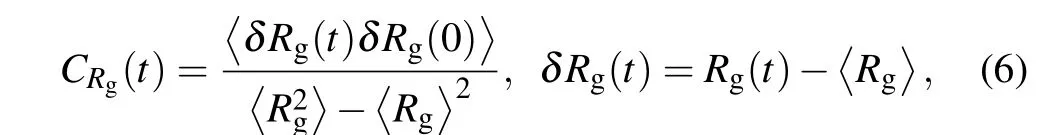
whereRgis radius of gyration of tethered PE chain.For clarity,the autocorrelation functions of shorter and longer PE chains atβ=1.0 andσg=0.029 for different interaction parameters between two ligands are plotted in Fig. 1, and others are similar to those four cases.

As shown in Fig. 1, it is noted thatCRg(t) of shorter(NA=24)and longer(NB=48)PE chains decays to zero before 1500τ(equal to 3.0×104time steps) in all illustrated cases, which is much shorter than the lasting time of equilibrated run (6.0×106time steps). Therefore, it is believable that the system approaches the steady state in the production run. Moreover,due to the curvature of grafting surface,there exist more free volume for the long chains away from the substrate, promoting the lateral swing of longer PE chains in a longer time scale, which leads to the fact that the fluctuation ofCRg(t) of short chains in Fig. 1(a) is smaller than that of long chains in Fig.1(b).

Fig. 1. Autocorrelation functions of radius of gyration of the grafted bidisperse PE chains at β =1.0 and σg=0.029 with different effective interaction parameters between the two ligands. (a) shorter PE chains NA=24,(b)longer PE chains NB=48.

3.1. Morphologies and properties of bimodal PE brushes at χAB=0

The surface patterns of the bimodal spherical PE brushes in the presence of trivalent counterions at different grafting densities as a function of mismatch parameterβare plotted in Fig. 2. Due to the absence of effective attractive/repulsive interaction between the two species of grafted PE chains atχAB= 0, the surface structures of binary mixed PE brush are induced by mismatch parameter, solvent-mediated interaction between monomers,and electrostatic correlation effect of trivalent ions.

For the low grafting densityσg= 0.029 shown in Fig.2(a),the bidisperse PE brush adopts an individual mushroom morphology atβ= 0. Specifically, the tethered PE chains demonstrate coiled configurations due to the electrostatic correlation effect of trivalent counterions. With the increase of mismatch parameterβ, the longer PE chains begin to aggregate with their neighboring short chains, the pinned-patch structure composed of a dense core and stretched surface-tethered “legs” are formed forβ ＞1.0. It is noted that the number of patches in the binary mixed PE brushes decreases with the increase of mismatch parameter (see the first row of Fig. 2(a)). For the grafting density increasing toσg=0.080 in good solvent, the enhancing excluded volume interaction is not strong enough to render the tethered PE chains encapsulate the whole substrate colloid, that is, a part of surface of central colloid are exposed. The micelle-like structure is observed atσg=0.318,which is regardless of the mismatch parameter (see the third row of Fig. 2(a)). The bimodal PE brushes are swollen uniformly with the increase ofβ.

As depicted in Fig. 2(b) in poor solvent solutions atχAB=0,the solvent-mediated segment-segment attractive interaction coupled with the electrostatic correlation of trivalent counterions induce the appearance of various pinned-patch morphologies atσg=0.029 and 0.080. In this regime, with increasingβ,fewer patches are formed for fixed grafting density. Whenβ=2.5 atσg=0.080,the two pinned patches are merged into one bigger aggregate,namely,a Janus-like structure is observed. The similar asymmetric morphology was also identified by Lane and Grest in the monodisperse spherical PE brushes experimentally in a poor solvent.[39]With increasing the grafting density toσg=0.318, the uniform collapsed brushes appear irrespective of mismatch parameter(see the third row of Fig.2(b)). Specifically,a series of island-like structures are found in the binary mixed PE brushes, which were also predicted by the SCF theory for the bimodal homopolymer brushes grafted onto a nanosphere.[10]

The global configuration of tethered bimodal PE chains is characterized by the shape factor, which is defined as〈R2e〉/〈R2g〉. Here,ReandRgcorrespond to the end-to-end distance and the radius of gyration of a grafted chain.[32]Specifically, the values of the shape factor are 2.0, 6.3, and 12, respectively,which correspond to the geometries of tethered PE chains to be spherical,coil-like,and rod-like.To further reveal the effects of mismatch parameter and solvent quality on the surface morphologies of bimodal PE brushes, the shape factors of two ligands atχAB=0 in both good and poor solvents are calculated respectively,and the results are plotted in Fig.3.

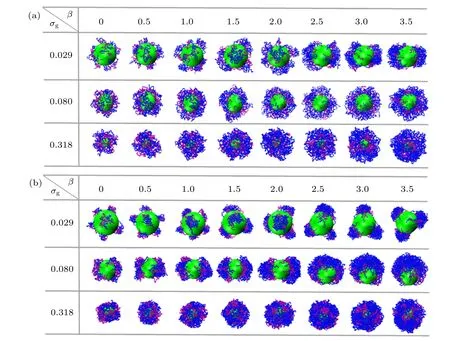
Fig.2. Snapshots of spherical bimodal PE brushes at different grafting densities σg as a function of mismatch parameter β: (a) χAB =0 and good solvent conditions,(b)χAB=0 and poor solvent conditions. The green sphere represents the grafting colloid. The purple and blue beads correspond to A-component and B-component,respectively.

Fig. 3. Shape factor of tethered PE chains as a function of mismatch parameter: (a) χAB =0 and good solvent condition, (b) χAB =0 and poor solvent condition. The solid and open symbols represent the cases of A-component and B-component PE chains,respectively.

As shown in Fig. 3(a), the shape factor of A-component chains increases slightly with the increase ofβat low grafting densityσg=0.029 (see solid circles), while the increasing trend of the shape factor atσg= 0.080 and 0.318 (see filled triangles and squares) becomes more pronounced. In contrast to the A-component chains,the value of〈R2e〉/〈R2g〉of B-component chains demonstrates an obvious decrease with the increase of mismatch parameter. The dependences of shape factor on the mismatch parameter clearly represent the coupling of electrostatic correlation effect mediated by trivalent counterions and excluded volume interaction effect of good solvent. Specifically, due to the low grafting densityσg= 0.029, excluded volume interaction is relative weak,the swelling of A-component chains can be attributed the inter-chain correlations of trivalent counterions, that is, the trivalent-counterion-mediated attractive segment-segment interaction renders the binary mixed PE chains aggregate to form heterogeneous surface patterns,leading to the stretching of the shorter PE chains. With further increase of grafting density,the enhancing excluded volume interaction combined with the electrostatic correlation effect is more facilitated to stretch the relative shorter PE chains. Furthermore, the shrink of long chains is due to the intrachain bridging of trivalent counterions and the curvature of substrate. Specifically, the end parts of long chains occupy the peripheral space of binary mixed PE brush and prefer to adopt the coiled configuration due to the translational entropy,in which the electrostatic correlation effect of trivalent counterions dominates and induces to the decreasing profile of longer PE chains.

Figure 3(b) shows the shape factors of tethered bimodal PE chains as a function of mismatch parameter atχAB=0 under poor solvent condition.Atσg=0.029,compared to a clear increasing of shape factor of shorter PE chains(see filled circles in Fig.3(b)),shape factor of long chains fluctuates obviously with the increase of mismatch parameter,as shown in the first row of Fig.2(b),which is due to a sequence of transitions from more pinned aggregates to less induced by the hydrophobic effect and electrostatic correlation effect. Atσg=0.080,a slight increase of shape factor of short chains is observed forβ ≤2.0 and then levels off in the large mismatch parameter rangeβ ＞2.0 (see solid triangles in Fig. 3(b)), which corresponds to the structural transition from two pinned patches to one patch demonstrated in the second row of Fig.2(b).The increase of shape factor of A-component chains and the decrease of shape factor of B-component chains with the increase of mismatch parameter are also observed at high grafting densityσg=0.318 in the poor solvent,which are similar to those profiles under good solvent conditions.

To reveal the local structure of the bimodal PE brush,we calculate the pair correlation function(PCF).The PCF between A-monomers and B-monomers atχAB=0 in good and poor solvent solutions are illustrated in Fig.4.For clarity,only four different mismatch parameters are provided without losing the regularity.

Fig. 4. Pair correlation functions between A-monomer and B-monomer for different mismatch parameters. Upper panels correspond to the case of χAB =0 and good solvent condition: (a)σg =0.029,(b)σg =0.080,(c)σg =0.318. Lower panels refer to the case of χAB =0 and poor solvent condition: (d)σg=0.029,(e)σg=0.080,(f)σg=0.318.

For the case of good solvent atχAB=0 shown in upper panels of Fig.4,one can find that(1)the primary peak of the PCF locates atr=2.2 and its amplitude decreases with the increase of mismatch parameter for fixed grafting density; (2)the secondary peak of PCF locates atr=3.6, which is more pronounced for the large value of mismatch parameter; (3) both the primary and the secondary peaks increase with the increase of the grafting density for the fixedβ. In contrast to the good solvent condition, the distinguished profiles of PCFgA−B(r)under poor solvent conditions atχAB=0 are illustrated in the lower panels of Fig. 4. Specifically, the three clear peaks,located atr=1.1,2.0 and 3.0,are emerged successively. These three peaks become unconspicuous with the increase of mismatch parameterβfor the fixed grafting density. The heights of the three peaks increase with the increase of the grafting density for the fixedβ. Based on the comparison between good and poor solvent conditions, it is noted that the nearest neighboring peak ofgA−B(r) located aroundr= 1.1 is absent for the good solvent case, which is attributed to the repulsive characteristic of solvent mediated excluded volume interaction. The electrostatic correlation,manifested as an attractive interaction between segments of the binary mixed PE chains, mediated by trivalent counterions, leads to the appearances of long-range order (peaks located aroundr=2.2 and 3.6) ingA−B(r) under good solvent condition. Hyeon and coworkers reported that the similar peaks located aroundr=2.0 and 4.0 in the interchain correlation profile when they conducted a molecular simulation of a monodisperse planar PE brush in trivalent salt solution,[40]which is similar to our result for the binary PE brush. The discrepancies may be induced by the polydisperse of tethered chains and the curvature of the substrate. While for the poor solvent case atχAB=0,the occurrence of the first peak aroundr=1.1 is attributed to the strong solvophobic-induced attractions between monomers. The observation of second and third peaks (aroundr=2.0 and 3.0) ofgA−B(r) under poor solvent conditions can be understood from the coupling effects between the interchain bridging of trivalent counterions and the hydrophobicity of solvent. Furthermore, it is worthy to notice that the locations of peaks induced by electrostatic correlations under poor solvent conditions are smaller than those in good solvent,which corresponds to the tight surface heterogeneous patterns (see Fig. 2(b)) induced by the hydrophobic effects of poor solvent.

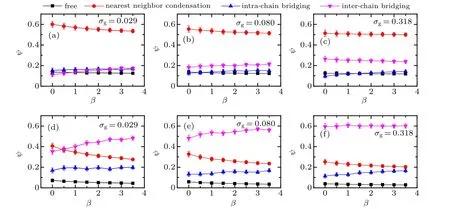
Fig.5.Fractions of trivalent counterions in the four states as a function of mismatch parameter at χAB=0.Upper panels are in the good solvent conditions: (a)σg=0.029,(b)σg=0.080,(c)σg=0.318. Low panels are in the poor solvent conditions: (d)σg=0.029,(e)σg=0.080,(f)σg=0.318.

Due to importance of electrostatic correlation of trivalent counterions in the surface morphologies of bimodal PE brush,we further study the states of trivalent counterions by classifying them into four states,[41–43]namely,the free,nearest neighbor condensation (NNC), intrachain bridging (IAB), and interchain bridging(IEB),respectively. The four factionsψfree,ψNNC,ψIAB,ψIEBare defined as the ratios of the number of trivalent counterions that are in the corresponding state to the total number of counterions. The state of trivalent counterion is identified by constructing the neighbor list of monomers for each trivalent counterion based on a cutoff distanceRc=21/6,which corresponds to the cutoff distance of the pairwise interations between monomer and counterion. Specifically, if no monomers in the neighbor list,the trivalent counterions are in free state. If monomers in the neighbor list belong to different tethered PE chains,the counterion is considered in IEB state,however, if the monomers in the neighbor list come from the single PE chain and the interval between the maximum index and minimum index of the neighbor list is larger than 2, the counterion is confirmed in IAB state, otherwise, it is in NNC state. The fractions of trivalent counterions as a function of mismatch parameter under good and poor solvent conditions atχAB=0 are illustrated in Fig.5.

As depicted in Fig. 5(a), the fractions of counterions in the free(filled squares)and NNC(filled circles)states demonstrate a slight decreasing profile with the increase ofβatσg= 0.029. However, the fractions of counterions playing the intra/inter-chain bridging role increase clearly with the increase of mismatch parameter, especially for theψIEB(filled down triangles). The enhancing trivalent counterion mediated attraction between charged segments induces the bimodal PE brush to adopt the pinned-patch structure, which can be seen in the first row of Fig.2(a). This is the manifestation of electrstaic-correlation-induced phase separation of PE brush,which is beyond the description of mean field theory.[44]The occurrence of pinned-patch structure is consistent with a recent phenomenological theory for PE brush collapse in the presence of multivalent ions.[45]Forσg= 0.080 shown in Fig. 5(b), the dependences of the four factions of trivalent counterions on mismatch parameter are similar with the correspondences atσg=0.029. With further increase of the grafting density toσg=0.318, the profile ofψIEBdrops slightly with the increase ofβ. Furthermore, the value ofψfreecan be qualitatively understood using Manning’s theory,[46,47]that is,in Manning’s theory,the fraction of free counterions is expressed asψfree=b/(lBfzc), whereb,f, andzcrefer to the interval of two adjacent charged monomers along the chain backbone,charge fraction,and valence of counterions,respectively.In our simulations,these parameters are set as:lB=3.0,f=1.0,andzc=3.0.The corresponding fraction of free counterions isψfree=0.11 based on the Manning theory.It is noted that theψfreedecreases from 0.13 to 0.11 with the increase of mismatch parameter in the upper panels of Fig.5,which coincides with the prediction of the Manning theory.

For the case of poor solvent conditions atχAB=0 shown in the lower panels of Fig. 5, almost all the trivalent counterions are condensed onto the polymer backbone due to the strong couter-effect of solvophobic-induced attractions between monomers.The fractions of counterions in IAB state increase slowly with the increase of mismatch parameter,which is almost irrespective with the grafting density. With the increase ofβ,ψNNCdecreases andψIEBincreases significantly.The trivalent counterions in IEB state are in the majority,which is more pronounced for the high grafting density (see filled down-triangles in the lower panels of Fig.5).

3.2. Morphologies and properties of bimodal PE brushes at χAB=0.9 and χAB=−0.9

The surface morphologies of spherical bimodal PE brushes with chemical distinct ligands are also explored and the snapshots are illustrated in Fig.6.

Due to the incompatibility between the A-monomer and B-monomer atχAB=0.9,the two tethered PE chains tend to form split pinned-micelle structure through lateral microphase separation, which are shown in Fig. 6(a). At low grafting densityσg=0.029,only a few tethered chains can aggregate into clusters at small mismatch parameters because of relative long distance between grafting points. With the increase of the mismatch parameter, the number of pinned patches formed by B-component chains decrease clearly(see the blue pinned micelles in the first row of Fig. 6(a)). The number of pinned patches of the two species monomers decreases significantly with the increase of grafting density. These A-monomer and B-monomer separated domains of bimodal PE brushes were also reported for mixed neutral PMMA/PS brushes experimentally.[17]It is worthy to notice that a series of interesting Janus-like structures can be observed atσg=0.318 induced by the increase of mismatch parameter,which was also observed in neutral two-component polymer brush.[17,48]

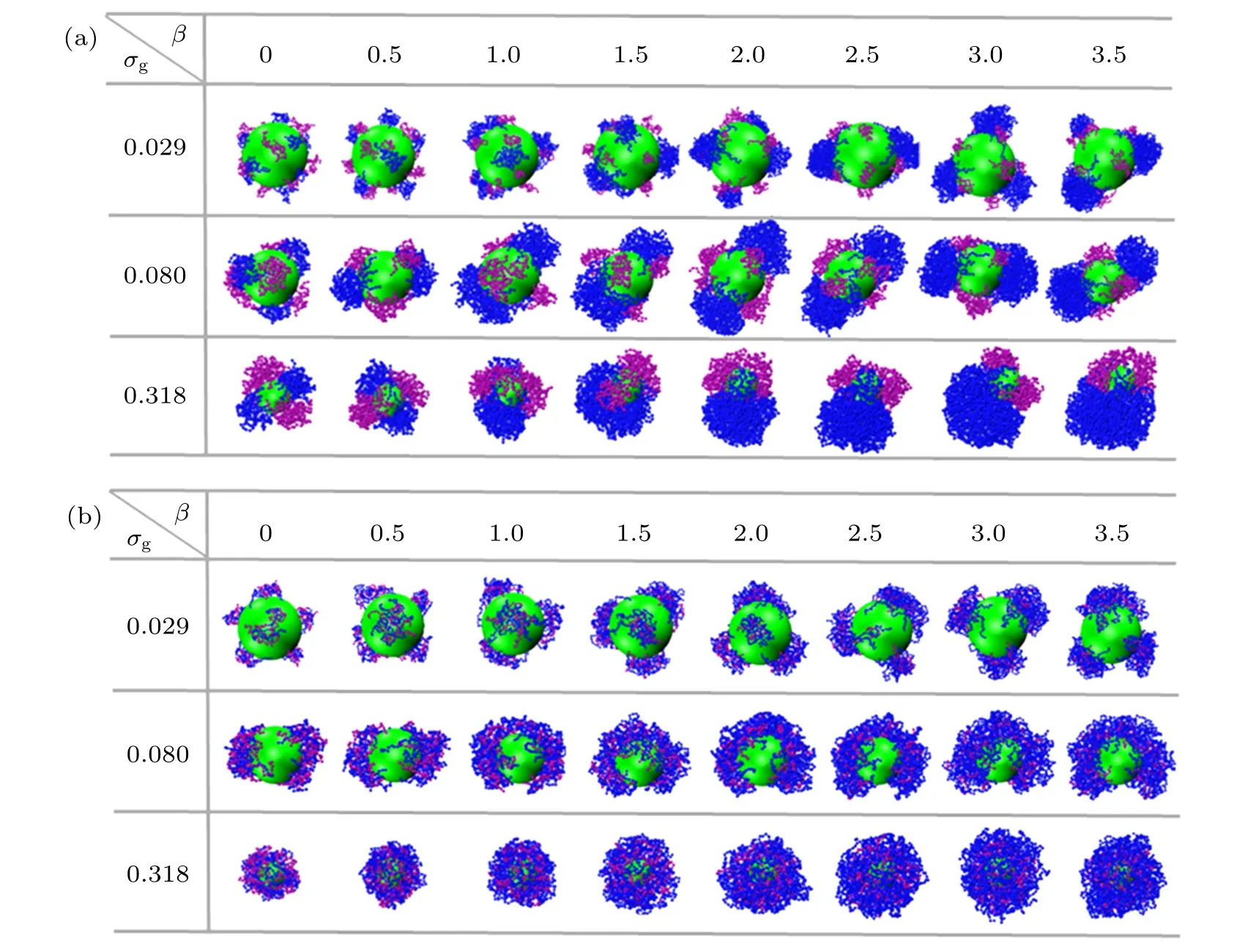
Fig. 6. Snapshots of spherical bimodal PE brushes at different grafting densities σg as a function of mismatch parameter β: (a) χAB = 0.9,(b) χAB =−0.9. The green sphere represents the grafting colloid. The purple and blue beads correspond to A-monomers and B-monomers,respectively.

As shown in Fig. 6(b), the hydrophilicity of the individual PE chain, the effective attraction induced by miscibility between the two ligands, and the electrostatic correlations of trivalent counterions are coupled together to induce the formation of pinned-patch structure at low grafting densityσg=0.029. The number of patches decreases with the increase of mismatch parameter,which demonstrates the similar trend with the case ofχAB=0 under poor solvent conditions shown in Fig. 2(b). It is interesting to point out that the two species of monomers are mixed uniformly in the surfaced patterns atχAB=−0.9, however, as depicted in the first row of Fig. 2(b), the shorter PE chains aggregate to form the inner part of the pinned patches,the long chains occupy the periphery of the surface patterns and surround the micelles formed by the short chains. Namely,the pinned patches are stratified due to the combination of poor solvent mediated attraction and electrostatic correlation of multivalent counterions atχAB=0 andσg=0.029, which were also observed in the mixed neutral homopolymer brushes emerged in various solvents.[5]For further increasing grafting density toσg=0.318,the uniform layer structures are formed and the polymer layers are relative loose compared with those atχAB=0 under poor solvent conditions shown in the third rows of Fig.2(b).

The dependences of shape factor of the two tethered PE chains on the mismatch parameter atχAB= 0.9 and−0.9 are plotted in Fig. 7. As shown in Fig. 7(a), the profile of shape factor demonstrates a clear fluctuation with the increase of mismatch parameter, especially for the longer PE chains(open symbols), which can be attributed to the lateral heterogeneities of surface morphology shown in Fig. 6(a). Specifically,the value of shape factor of shorter PE chains is almost irrespective with mismatch parameter at all the three grafting densities,which is due to the immiscibility of the two ligands.For the longer PE chains,the shape factor demonstrates three different profiles with the grafting density, that is, increases clearly atσg=0.029,remains unchanged and then decreases atσg=0.080, decreases gradually atσg=0.318, which can be understood from the curvature of substrate.Specifically,the long polyions must be stretched more strongly to form pinned micelle structure with the increase ofβ, which results to a large value of shape factor at low grafting density.As shown in Fig. 7(b), when the effective interaction between two species of chains is attractive,the effect of mismatch parameter on the shape factor is more pronounced than that atχAB=0.9. The discrepancies of the value of shape factor between shorter and longer PE chains increase obviously with the increase ofβfor fixed grafting density, which is attributed to the effective attraction between polymer backbones atχAB=−0.9.

The PCFs between A-monomer and B-monomer atχAB=0.9 and−0.9 are also calculated, and the results are plotted in Fig. 8. One can imagine that the pair correlations are relative weak atχAB=0.9 because of the immiscibility between two tethered PE chains,which is in fact demonstrated in the upper panels of Fig. 8. Specifically, the low and wide primary peak ofgA−B(r) atχAB= 0.9 is solely attributed to the electrostatic bridging of trivalent counterions. Since the solvent-mediated inter-chain attraction between tethered chains is dominated atχAB=−0.9,both the nearest neighbor correlation and the long-range correlation between two species become pronounced,which is manifested as the emergences of two clear peaks ingA−B(r). The first peak is located aroundr=1.1 corresponding to the miscibility of two tethered chains induced by selectivity of solvent,and the second peak is close tor=2.0, which is due to the electrostatic correlation effect of trivalent counterions.

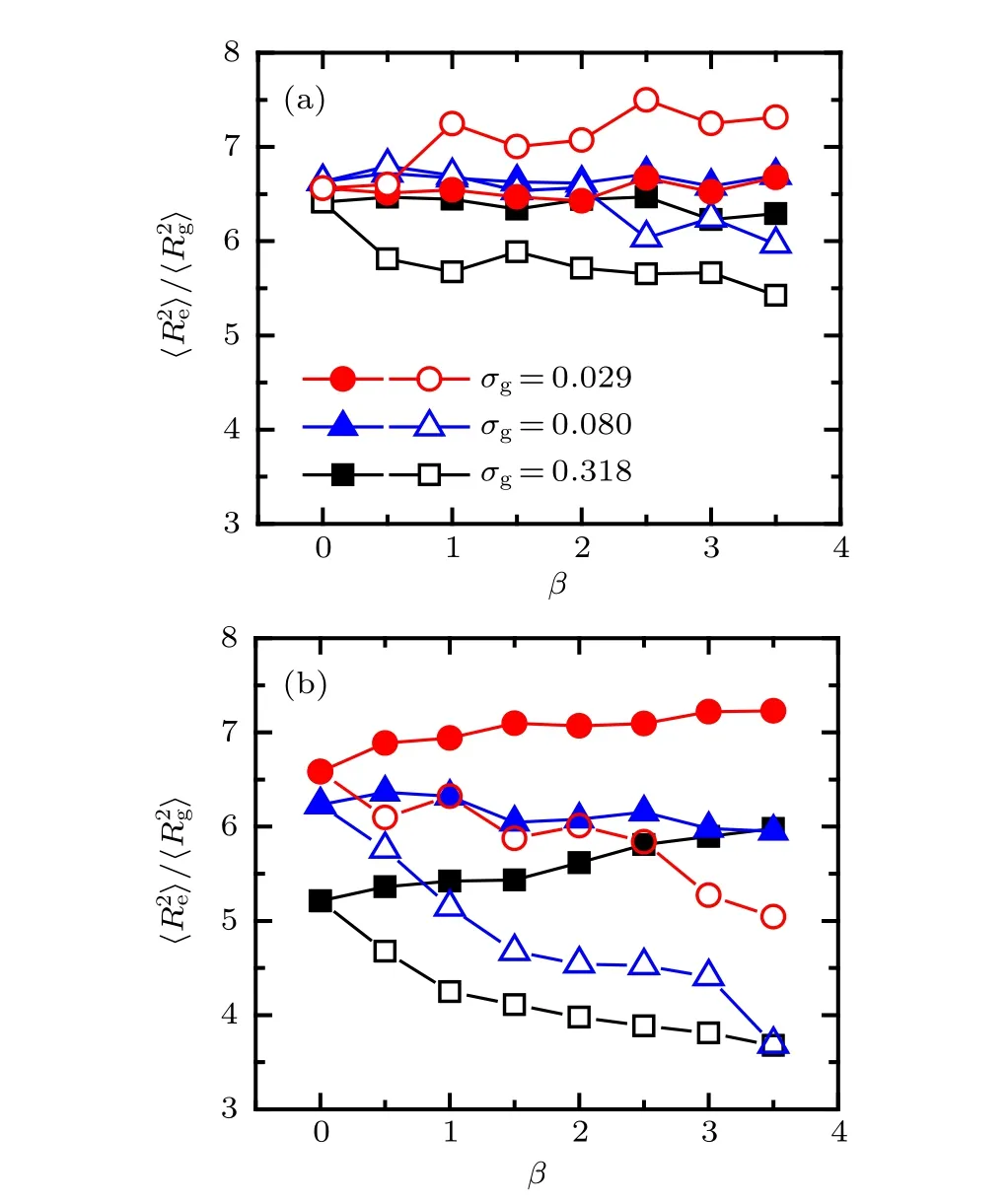
Fig.7.Shape factor of tethered PE chains as a function of mismatch parameter at different grafting densities: (a) χAB =0.9,(b) χAB =−0.9.The solid and open symbols represent the case of A-component and B-component PE chains respectively.

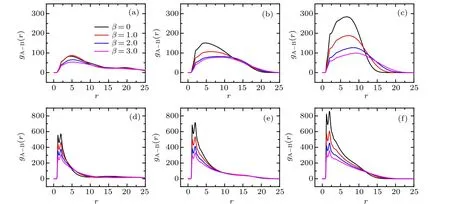
Fig.8. Pair correlation functions between A-monomer and B-monomer for different mismatch parameters at different grafting densities. Upper panels correspond to the case of χAB=0.9: (a)σg=0.029,(b)σg=0.080,(c)σg=0.318. Lower panels refer to the case of χAB=−0.9: (d)σg=0.029,(e)σg=0.080,(f)σg=0.318.

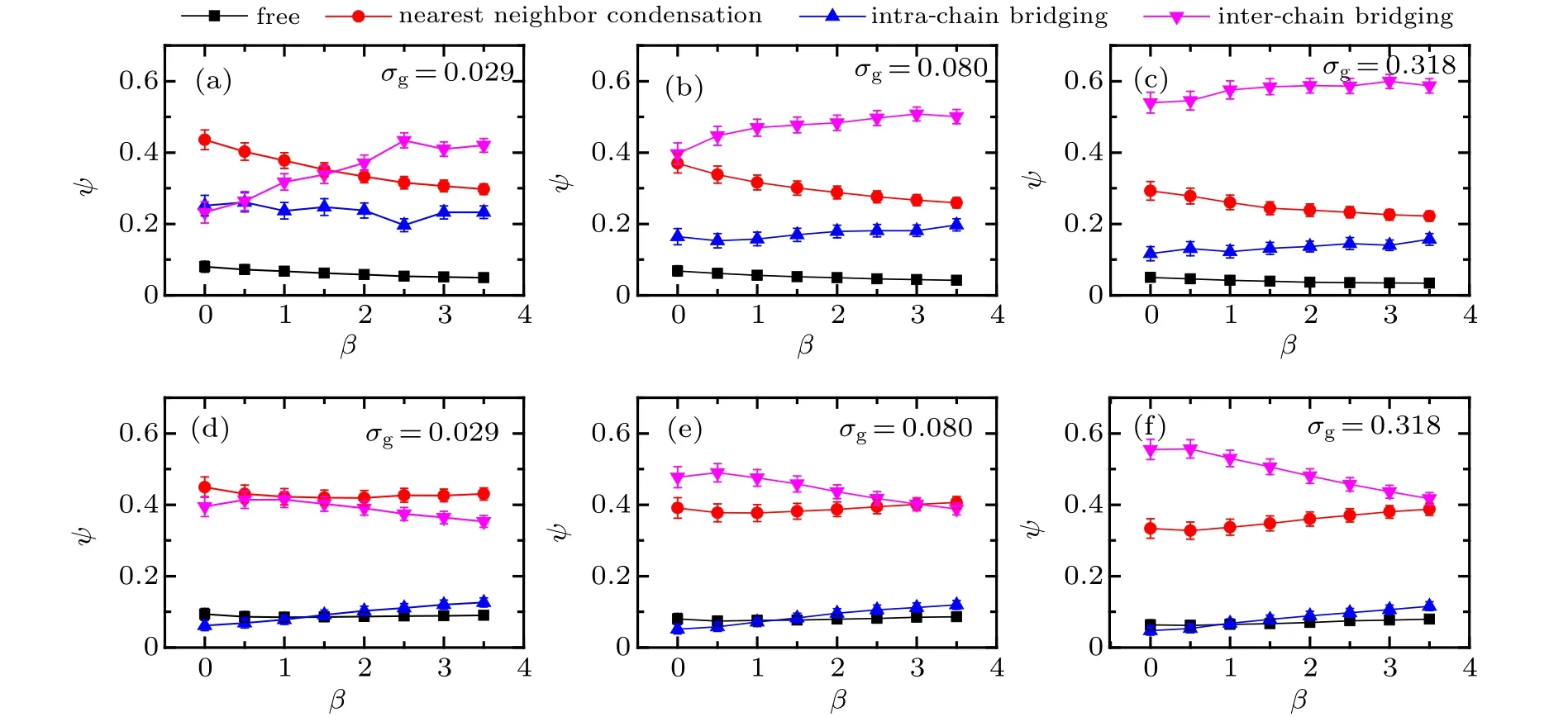
Fig.9.Fractions of trivalent counterions in the four states as a function of mismatch parameter at different grafting densities.Upper panels refer to the case of χAB=0.9: (a)σg=0.029,(b)σg=0.080,(c)σg=0.318. Low panels correspond to the case of χAB=−0.9: (d)σg=0.029,(e)σg=0.080,(f)σg=0.318.

To identify the electrostatic correlation effect of trivalent counterions on the surface morphologies of bimodal PE brushes with two chemical distinct ligands, the fractions of counterions in the four states are further calculated based on the similar definition with those in Fig.5. The dependences of fractions of trivalent counterions on mismatch parameter for different grafting densities atχAB=0.9 and−0.9 are plotted in Fig.9.

As shown in the upper panels of Fig.9,less than 10%of trivalent counterions are in free state atβ=0, and theψfreedrops slightly with the increase of mismatch parameter,which are similar for the three different grafting densities(see filled squares). The fraction of counterions in NNC state decreases obviously with the increase ofβregardless of grafting density,leading to the increase of fractions in the intra/interchain bridging states. Specifically, the increase of fraction of trivalent counterions in IEB state is dominated atσg=0.029,however, bothψIABandψIEBdemonstrate a clear increasing profile with the increase of mismatch parameter for the increasing grafting density toσg= 0.080 and 0.318. Most of the trivalent counterions play the IEB role at high grafting densityσg=0.318(see down-triangles in Fig.9(d)). ForχAB=−0.9 illustrated in the lower panels of Fig.9,the fractions of trivalent counterions in free and IAB states are around 0.1, which are independent of grafting density.It is interesting to note that the curve ofψNNCdrops slightly, and then increases clearly with the increase ofβ(see filled circles), which is reversed compared to the profile ofψIEB(see filled down triangles).The intersection of these two curves shifts to the largeβdirection with the increase of grafting density,which represents the variation of delicate balance between the electrostatic correlation and translational entropy of trivalent counterions induced by excluded volume interaction.

4. Conclusions

In summary, we have performed MD simulations of spherical bimodal PE brushes with trivalent counterions in response to the selectivity of solvent. The effects of grafting density and mismatch parameter of chain length on the surface morphologies are investigated systematically. AtχAB=0,the increase of mismatch parameterβenables the long chains to gather the neighboring short chains together to form pinnedpatch structures at low grafting density. These heterogeneous surface patterns are solely induced by the electrostatic correlations of trivalent counterions in good solvent, which has been confirmed in PE brushes formed by monodisperse chains. The pinned-patch morphology is more tightly packed under poor solvent condition, which is due to the combination of the electrostatic correlation of multivalent counterions and the solvent-mediated attractive interaction between monomers. The micelle-like structure is observed at high grafting density due to the domination of excluded volume interaction.

AtχAB＞0, the effective repulsion between two ligands coupled with the electrostatic bridging effect of trivalent counterions render the tethered PE chains to form pinned-patches independently, that is, the microphase separated domains are formed by the two species of monomers respectively. The number of patches in a bimodal PE brush decreases with the increase of mismatch parameter and grafting density. For the case ofχAB＜0,the combined effect of the solvent-mediated attraction and the electrostatic correlation mediated attraction between the bidisperse PE chains promotes the appearance of pinned-patch structure at low grafting density.The two species of monomers are evenly mixed in the patches,which is distinct with those in the patches formed atχAB=0.The shape factors are calculated to reveal the global configurations of the two ligands. The PCFs of A-monomer and B-monomers are employed to clarify the different orders induced by polydispersity and solvent selectivity. Furthermore, trivalent counterions in the bimodal PE brush system are carefully classified into four states to pinpoint their roles in the electrostatic correlation effect. Our systematic analysis may be used to guide the design of responsive,nanostructured polymer-inorganic hybrid materials for potential applications based on mixed PE brushes.