Magnetic impurity in hybrid and type-II nodal line semimetals∗

Xiao-Rong Yang(杨晓容), Zhen-Zhen Huang(黄真真), Wan-Sheng Wang(王万胜), and Jin-Hua Sun(孙金华)

Department of Physics,Ningbo University,Ningbo 315211,China

Keywords: hybrid nodal line semimetals,type-II nodal line semimetals,Anderson impurity,Kondo screening

1. Introduction

Topological semimetals,[1,2]represented by the Dirac semimetals (DSMs), Weyl semimetals (WSMs), and nodal line semimetals (NLSMs), are a new class of quantum matter, and have been predicted in theories and realized in experiments. Different from the DSMs/WSMs whose conduction and valence bands touch at discrete points, the NLSMs are those with the bands cross in one-dimensional lines in the momentum space.[3–5]In most studied NLSMs, the density of states(DOS)is proportional to(E −EF)2,and the NLSMs normally have drumhead-like surface states. By comparison,the DOS is proportional to (E −EF) in type-I DSMs/WSMs,and the Weyl nodes are connected by 1D Fermi arc surface states in the WSMs.[6]In analogous to the WSMs, the NLSMs can also be categorized into three types, depending on the electronic structure of the bands. To date, type-I NLSMs have been intensively studied both theoretically[7–21]and experimentally.[13,20–25]The type-II NLSMs are those with closed nodal lines but the local cones along the lines become tilted.[26,27]The hybrid NLSMs are proposed to have a partially over-tilted linear dispersion at the nodal loop. It has been reported that the type-I,type-II,and hybrid NLSMs can be realized in a realistic material, i.e., quasi-2Dα-FeSi2, by strain switching.[28]

The purpose of this paper is to investigate the properties of the Kondo screening in the hybrid and the type-II NLSMs.The Kondo effect arises from the interactions between the local magnetic atom and the conduction electrons, and the Kondo effect in a normal metal has been widely studied and well understood.[29]One of the reasons that this seemingly“old” problem still receives great research interest is due to the rapidly emerging novel materials with intriguing dispersion and topological properties. In the type-I DSMs/WSMs,the DOS vanishes if the Fermi level lies right at the nodes,and the Kondo problem in such systems falls into the category of pseudo-gap Kondo problem.[30–32]The magnetic impurity and the conduction electrons form a bound state only if the hybridization between them exceeds a critical value. In Lorentzviolating host systems like tilted Dirac surface states and type-II WSMs, the formation of the impurity-conduction electron bound states is also determined by the DOS of the Fermi surface,and the spatial screening shows very rich features due to the unique dispersion relations.[33,34]

In this paper,we systematically study the binding energy and real space spin–spin correlations of a magnetic impurity in both the hybrid and type-II NLSMs. The variational method we apply has been used to study the ground state of the Kondo problem in normal metals,[35,36]antiferromagnet,[37]2D helical metals,[38]3D Weyl semimetals,[34,39]tilted Dirac surface states,[33]type-I NLSMs[40]and multi-WSMs,[41]and the Fermi arc surface states of WSMs.[42]Due to the intriguing nodal loop structure of the hybrid and type-II NLSMs, the Kondo screening in these systems is expected to show very interesting features.

The paper is organized as follows. We present the model and dispersion relation in Section 2. By using the model Hamiltonian we adopt, one can easily obtain different types of NLSM by tuning the parameters:[43]the system is a type-I NLSM with the tilting ratios|m·wx|＜0.5 and|m·wy|＜0.5,and is a type-II NLSM if|m·wx|＞0.5 and|m·wy|＞0.5. For the rest of the cases,the model Hamiltonian describes a hybrid NLSM.In Section 3,we apply the variational method to study the binding energy. In Section 4,we investigate the spin–spin correlation between the magnetic impurity and the conduction electrons in the hybrid and the type-II NLSMs. Finally, the discussions and conclusions are given in Section 5.

2. Anderson model Hamiltonian

We consider a spin-1/2 magnetic impurity in a 3D NLSM,and the Anderson model Hamiltonian writes

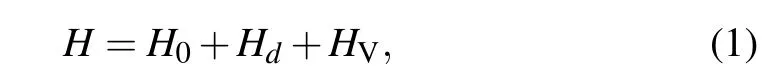
in whichH0describes the NLSM,Hdis the magnetic impurity part, andHVis the hybridization between the magnetic impurity and the conduction electrons of the NLSM.

The NLSM is given by[3,14,15,40,43–45]

wherek2i ≡k2x+k2y+k2zandwik2i ≡wxk2x+wyk2y+wzk2z,m ＞0 is the effective mass.∆is the radius of nodal ring projected onto thekx–kyplane, and we choose∆as the energy unit.µis the chemical potential,andνis the Fermi velocity in thezdirection. The basis is given byck={c1k↑,c1k↓,c2k↑,c2k↓}T,

wherecjk↑(j=1,2) andcjk↓are the annihilation operators of spin-up and spin-downj-orbital electrons,respectively.σα(α=x,y,z)andταare spin and orbital Pauli matrices,andσ0andτ0are identity matrices.In this model Hamiltonian,different types of NLSMs are conveniently obtained by tuning the tilting ratios:[43](1)if|m·wx|＜0.5 and|m·wy|＜0.5,h0describes a type-I NLSM,(2)if|m·wx|＞0.5 and|m·wy|＞0.5,h0describes a type-II NLSM,(3)for the rest of the cases,h0shall be the Hamiltonian of a hybrid NLSM.

The local magnetic impurity Hamiltonian is given by

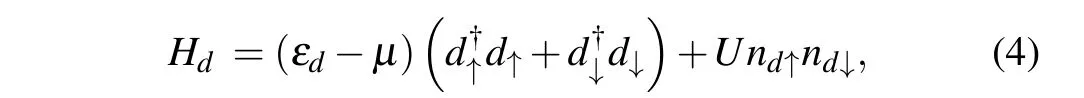
whered†↑(↓)andd↑(↓)are the creation and annihilation operators of the spin-up (spin-down) state on the impurity site.εdandUare the impurity energy level and on-site Coulomb repulsion,respectively. The hybridization between the magnetic impurity and the host material is described by

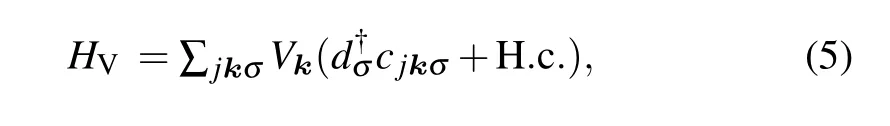
whereVkis the hybridization strength. Here we assume that the magnetic impurity is equivalently coupled to the two orbits in the NLSM for simplicity. Without loss of generally,we choose the position of the impurity as the originr=0, such that the hybridizationVkis in fact independent of momentum and orbits.

One can easily obtain the single-particle eigenenergy ofh0(k),

wherej=1,2 labels the orbits ands=1,2 labels the bands.Note that the bands are two fold degenerate, and the corresponding eigenstate operators are given by

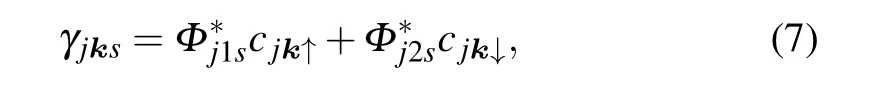
whereΦj1sandΦj2sare defined in Appendix A.

In Fig.1,we show the band structure and DOS of the hybrid and the type-II NLSMs. The band structures shown are plotted in thekx–kymomentum space withkz=0.

Fig.1. Schematics of the band structure and the nodal ring of(a)a hybrid NLSM and (b) a type-II NLSM for kz =0. The nodal rings are formed by the crossing between two different bands. (c)The finite DOS per unit cell of a hybrid NLSM, and (d) the DOS of a type-II NLSM. For type-II NLSM,the lowest energy state lies at energy/∆=−1,so the DOS below−∆is zero,and it increases monotonically with the energy.

As shown in Fig.1(a),the nodal ring of the hybrid NLSM is formed by the crossing between the parabolic bands and the saddle-shaped bands. In thekx–kyplane, the nodal ring satisfiesk2x+k2y=2m∆, and one can see clearly that the nodal ring has energy variation along the loop, with the scale between−2m∆wxand−2m∆wy. In Fig.1(b),we show the band structure of a type-II NLSM.Different from the hybrid NLSM case,the nodal ring in the type-II NLSM lies at the energy of−2m∆wy. In Figs. 1(c) and 1(d), we show the DOS per unit cell for the hybrid and the type-II NLSMs, respectively. The DOS is directly affected by the choice ofwivalues. If we fix the value of|m·wy|＞0.5, in the hybrid NLSM regime, as|m·wx|=|m·wz|increases from 0.1 to about 0.5,the DOS increases accordingly.|m·wx|=|m·wz|=0.5 is a critical point at which the system transits from a hybrid to a type-II NLSM.|m·wx|=|m·wz|＞0.5 describes the type-II regime, where the DOS results are drastically distinct from those in the hybrid regime. In the type-II NLSMs, the DOS is much lower,and most typically,the DOS below−∆vanishes. As shown in Fig.1(c),the DOS is larger around the charge neutrality point for the hybrid NLSM, and the DOS is always finite. Thus,one can expect that the impurity and the conduction electrons always form a bound state. For the type-II NLSM shown in Fig. 1(d), the DOS is zero if the energy is below−∆, independent of the model parameterswiandν. For the cases that energy is above−∆, the DOS increases monotonically with the energy level. In general,the DOS around the charge neutral point is much larger in the hybrid NLSM than that in a type-II case.

3. Self-consistent calculation

We utilize the well-known trial wavefunction approach which has been used to study the ground state of the Anderson impurity problem in the conventional metal,[35,36]2D helical metals,[38]antiferromagnets,[37]and various novel topological insulators[46]and topological semimetals.[33,34,39,42]We assume that the Coulomb repulsionUis large enough, and the impurity energy levelεdis below the Fermi energy,so that the impurity site is always singly occupied by a local moment.For the simplest case, we first discuss the case ofHV=0, in which the magnetic impurity and the NLSM are completely decoupled from each other.

The ground state ofH0is given by

where{jks}means the product runs over all the states inside the Fermi surface. The total energy of the system is just the sum of the energies of the NLSM and of the bare magnetic impurity

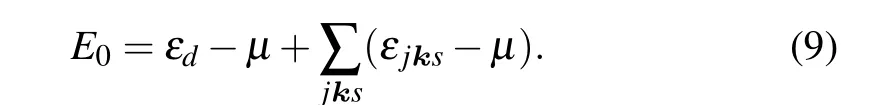
Then we move on to take into account the hybridization,the trial wave function for the ground state is

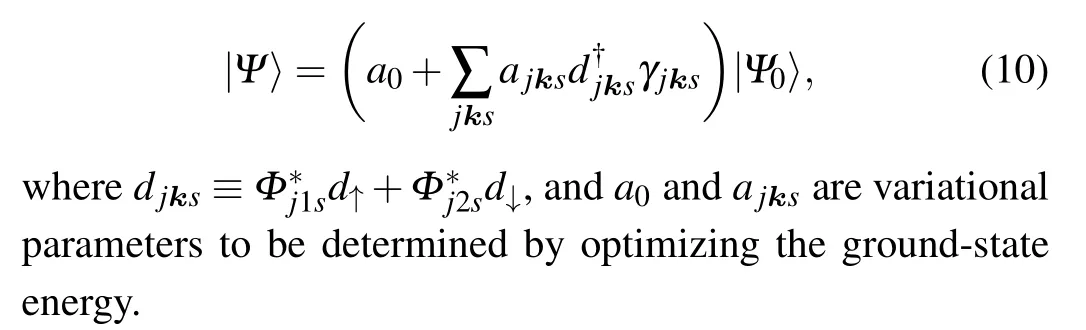
The energy of the Hamiltonian in variational state|Ψ〉is

The variational method requires that∂E/∂a0=∂E/∂ajks=0,from which we can obtain the following two equations:

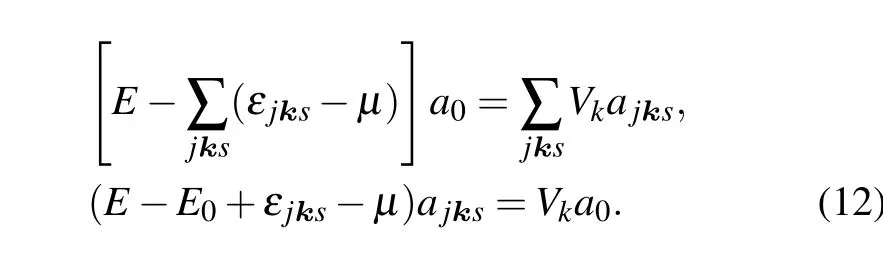
We defind the binding energy as∆b=E0−E, then the selfconsistent equation is given by

By numerically solving Eq.(13), we can obtain the values of∆b.∆b＞0 means that the hybridized state has lower energy than the bare state,such that the hybridized state is more stable.In our numerical calculations,the hybridization strength isVk=VΘ(Λ −|εjks|),whereΘ(x)is the Heaviside step function andΛis the energy cutoff. The Kondo effect is mainly influenced by the conduction electrons near the Fermi surface,so if we choose large enough values ofΛ, the Kondo effect shall be insensitive to the values of the energy cutoff. The energy cutoffs for both the hybrid and type-II NLSMs are chosen asΛ=100∆,where∆is the energy unit introduced in the NLSM Hamiltonian in Eq.(3).

Figure 2 shows the dependence of the binding energy∆bon the effective hybridizationΓfor different values ofµ. In here and below,we fix the parameters asm=0.005∆−1˚A−2,ν=10∆˚A,and the impurity energy level asεd=µ−0.01∆.We usewx=wz=−20∆˚A2andwy=−200∆˚A2for the hybrid NLSM,whilewx=wy=wz=−200∆˚A2for the type-II NLSM.

Note that actually the types of the NLSMs are not affect by the choice ofwz. However,by choosingwz=wxin our numerical calculations,the system shall preserve higher symmetry property,such that the analysis on the spin–spin correlation might become clearer. As illustrated in Fig. 2(a), for a fixed value ofΓ,the binding energy is the largest whenµ=−0.6∆,and the smallest ifµ=30∆. This result is consistent with the results of DOS shown in Fig.1(c). The binding energy is mainly influenced by the DOS at the Fermi energy, and the bound state is more easily formed when the DOS is large.For the hybrid NLSM,the DOS is always finite,so a positive binding energy always emerges for any finite values ofVk. In Fig.2(b),we can see that for a certain value ofΓ,the binding energy increases monotonically with the values ofµ,which is also consistent with the DOS results given in Fig. 1(d). Notice that for relatively smallΓ, the binding energies for both cases are also very small,but finite. It is well-known that the binding energy is positive only if the hybridization exceeds a critical value if the DOS is zero, but the binding energy shall always be positive for any finite hybridization.[33,34,38,39,42,47]

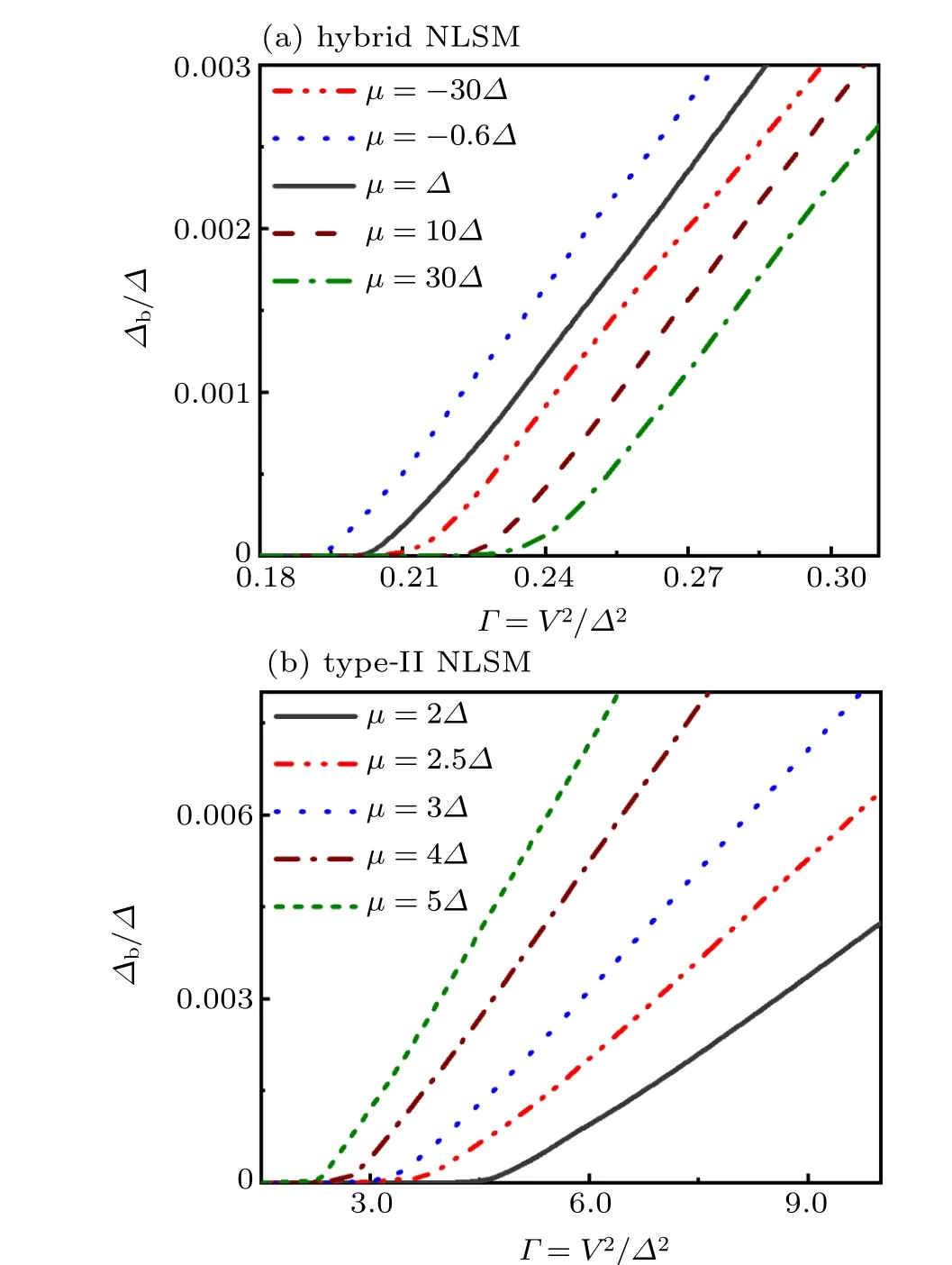
Fig.2. Binding energy ∆b of a magnetic impurity(a)in a hybrid NLSM and(b)in a type-II NLSM as a function of the effective hybridization Γ for different chemical potentialµ.

4. Spin–spin correlation

whereu,v=x,y,zare the spin indices and〈···〉denotes the ground state average. One can see that the NLSM Hamiltonian given in Eq. (3) is invariant under combined operationsT Ry(π),T Rz(π), andRx(π), whereTis the time-reversal operation andRu(π) (u=x,y,z) is the rotation of angleπabout theu-axis. For example, considering the invariance under the combined operationT Ry(π), one can prove thatJuv(r)=Juv()in thex–yplane,where=(−x,y,z).

The diagonal terms and the non-zero off-diagonal terms of the spin–spin correlation function are given by

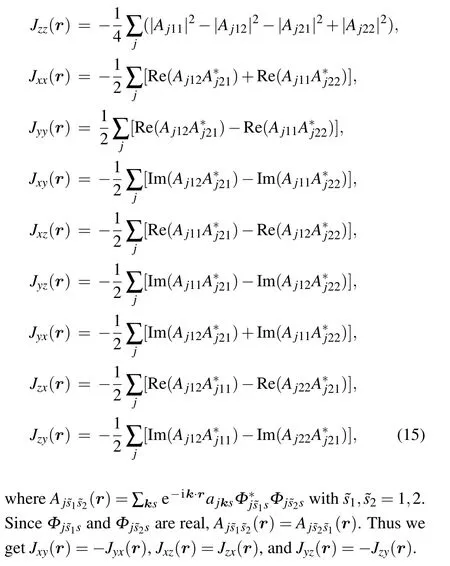
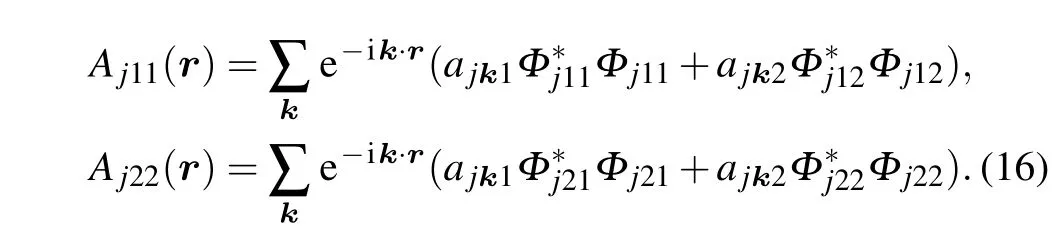
One can easily prove thatAj11(r) =Aj22(r), soJyy(r) =Jzz(r). Thus we only show the term of the spin–spin correlationrnJyy(r)in Figs.3–7.

In Fig.3,one can see that the spin–spin correlation functions along all the three spatial directions,x-,y- andz-axes decay with power law 1/r2. The momentum cutoffkcis chosen with respect to the energy cutoffΛ. The major difference is that the off-diagonal terms are all zero along thex- andydirections,but one off-diagonal termJxy(r)is finite along thez-axis.

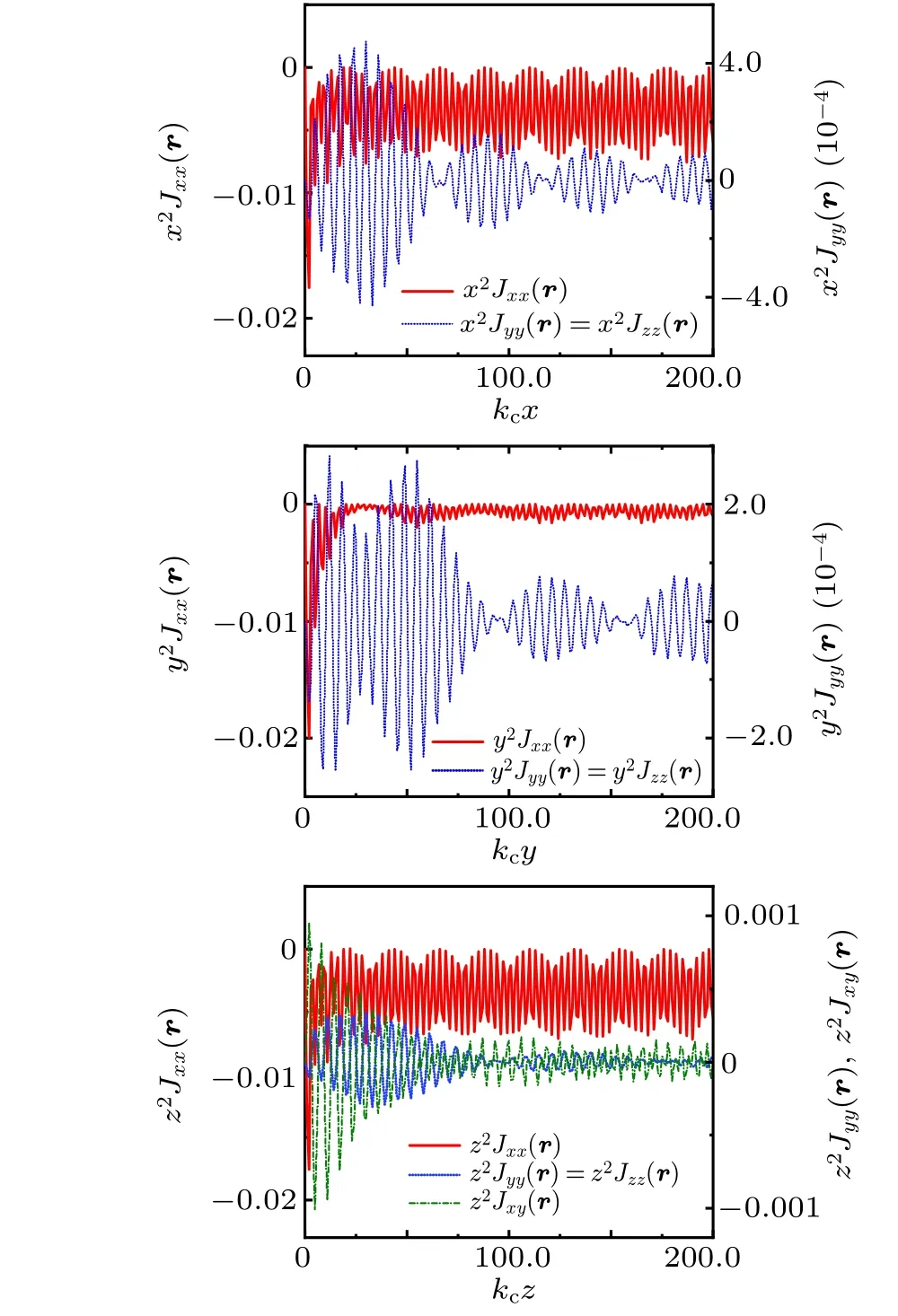
Fig. 3. Spin–spin correlations in a hybrid NLSM decay at the power of 1/r2 along the x-, y-, and z-axes at long distance. r2Jxx(r) along the x-axis decays in the same way as that along the z-axis. kc is the momentum cutoff chosen with respect to the energy cutoff Λ.

Fig. 4. Various components of the spin–spin correlation function in a type-II NLSM decay at the power of 1/r3 along the three coordinate axes at long distance. Due to the rotational symmetry about the z-axis,Juv(x)is exactly the same as Juv(y).

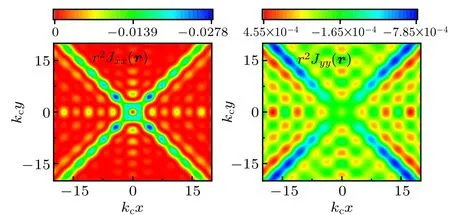
Fig. 5. Terms of the spin–spin correlation r2Juv(r) (u,v=x,y,z) in the x–y coordinate plane for a hybrid NLSM.All the off-diagonal terms vanish in the x–y plane,so they are not shown.

The spin–spin correlations between the local magnetic impurity and the conduction electrons in different 2D coordinate planes are given in Figs. 5–7. In Fig. 5 we show the spin–spin correlations between the magnetic impurity and the conduction electrons in a hybrid NLSM in thex–yplane. The tilting ratios of the NLSM model Hamiltonian are|m·wx|=|m·wz|=0.1 and|m·wy|=1. The system is invariant under the operations ofT Ry(π) orRx(π), so the spin–spin correlations in thex–yplane is symmetric with respect to thex-andy-axes.Jxx(r) is always antiferromagnetic and oscillates as|r|increases. The other two diagonal terms have the relationJyy(r)=Jzz(r), and all the off-diagonal terms vanish in this plane. In fact, the contributions from two different NLSM orbits cancel each other forJxz(r) andJyz(r). ForJxy(r),considering the symmetry operations, we can getJxy(x,y)=−Jxy(−x,y)=Jxy(−x,−y)=−Jxy(x,−y)=0,which is different fromx–zandy–zplans.

In Fig.6,we show the spin–spin correlations in the(a)x–zplane(top row)and(b)y–zplane(bottom row).Note that the off-diagonal termJxy(r)is nonzero in both planes. In thex–zplane, according to symmetry under the combined operationT Rz(π), one can easily know thatJxy(x,z)=Jxy(−x,z), such thatr2Jxy(x,z)is symmetric with respect to they-axis.Considering the operationRx(π),Jxy(x,z)=−Jxy(x,−z),and ifz=0 the off-diagonal termJxy(x,z) is always zero. Analogously,Jxy(y,z) is always zero ifz=0, which is caused by the symmetries aboutx-axis in they–zplane plus the two combined operationsT Ry(π)andT Rz(π). The diagonal terms in thex–zplane andy–zplane are symmetric with respect to the axes.Due to the unique band structure and the spin–orbit coupling,the spin–spin correlations shows strong anisotropy in different planes,and among the different diagonal components.

Fig.6. The r2Juv(r)(u,v=x,y,z)in the(a)x–z plane and(b)y–z plane for a hybrid NLSM.All the other off-diagonal components not shown are zero.

Fig.7. The diagonal terms of the spin–spin correlation r3Juv(r)(u,v=x,y,z)of the type-II NLSM in(a)x–y plane and(b)x–z plane. All the off-diagonal terms vanish in the type-II NLSM.

5. Conclusions

In summary, we study the Kondo screening effect of a spin-1/2 magnetic impurity in the hybrid and type-II NLSMs.The NLSM model Hamiltonian we adopt has the advantage that by expediently tuning the model parameters different types of NLSMs are realized: (a)a type-I NLSM if|m·wx|＜0.5 and|m·wy|＜0.5,(b)a type-II NLSM if|m·wx|＞0.5 and|m·wy|＞0.5,(c)a hybrid NLSM for the rest of the cases. In our calculation,|m·wx|=|m·wz|=0.1 and|m·wy|=1 are used for a hybrid case,while|m·wx|=|m·wy|=|m·wz|=1 are used for a type-II case.

The Kondo effect of a single magnetic impurity in a type-I NLSM has been studied,and it has been reported that when the chemical potential lies at the nodal loop,the magnetic impurity and the conduction electrons form bound states only if their coupling exceeds a critical value and the spatial decay ratio is either proportional to 1/r2or 1/r3, depending on the real space directions.[40]

Distinct from the type-I case already studied,in the hybrid and type-II NLSMs discussed in this paper,the DOS is always significant,so the magnetic impurity and the conduction electrons always form bound states. The DOS of the hybrid case is much larger than that of the type-II case, so in general the binding energy takes larger values in the hybrid case.

The spatial spin–spin correlations between the magnetic impurity and the conduction electrons shows anisotropic patterns,which can be discussed using the symmetry analysis of the host materials,and decays withr−2in hybrid NLSMs,and followsr−3decay in type-II NLSMs. This behavior is independent of the chemical potential and DOS, and is also independent of real space axis directions. Ther−3decay behavior in our type-II NLSM Hamiltonian is qualitatively consistent with the results obtained in the type-I case,[40]considering that the dispersion relation contains quadratic terms along thekz-axis. However, ther−2decay rate observed in the hybrid NLSM is much distinct from the type-I and type-II cases. Overall, the spatial decays in the hybrid and type-II NLSMs are different from that in a nomal metal,[48,49]and in the DSMs/WSMs.[39]This interesting feature can possibly work as a fingerprint to distinguish different types of NLSMs in experiments.

Appendix A

According Eq.(3),by diagonalizing this Hamiltonian,we obtain the eigenvalues

The transform matrix is defined as

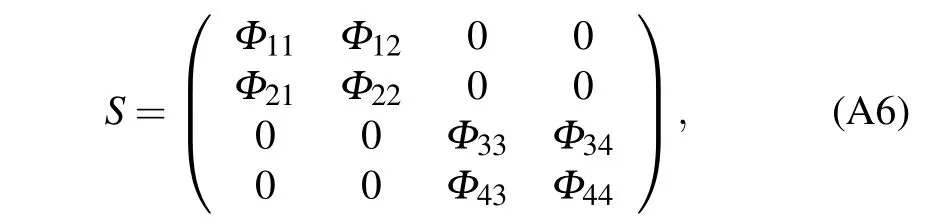
and sinceSis a unitary matrix, we haveS†=S−1. Then the Hamiltonian can be written as

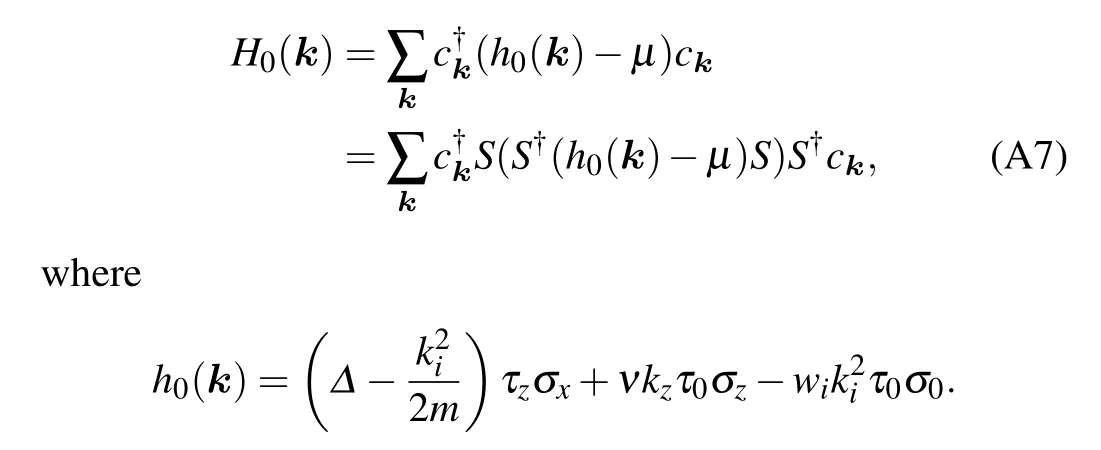
Because the two orbits in the NLSM are not coupled with each other,for the convenience of expression,we re-define the non-zero diagonal blocks of theSmatrix as two 2×2 matrices

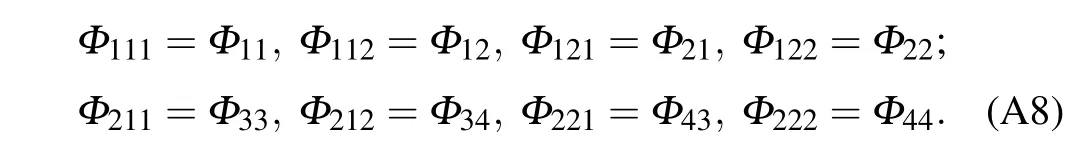
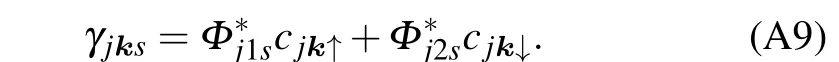
According Eq. (5), we can obtain the transformation ofdoperators as