Superfluid states in α–T3 lattice∗

Yu-Rong Wu(吴玉容) and Yi-Cai Zhang(张义财)

School of Physics and Materials Science,Guangzhou University,Guangzhou 510006,China

Keywords: superfluid states,flat band,α–T3 lattice,particle–hole symmetry

1. Introduction

The discovery of graphene has great significance in the developments of condensed matter physics. Graphene was first proposed in 1947,[1]and Novoselv and Geim experimentally prepared it in 2004.[2]Graphene is a two-dimensional material composed of carbon atoms which are arranged in a hexagonal to form a honeycomb lattice. In graphene, Dirac-Weyl Hamiltonian with pseudospinS=1/2 can be used to describe its low-energy behaviors.[3–5]The interests in graphene are largely due to its unique band structures and massless lowenergy excitation.[6–8]

For researchers, it is interesting to find new twodimensional materials similar to graphene. The honeycomb lattice structure of graphene provides a favorable reference for the study of other new models. Adding an atom to the center of nonequivalent “rim” sites on the hexagon gives a dice lattice.[9–12]The low-energy excitation of the dice lattice is also described by the Dirac equation,but its pseudospinS=1 instead of 1/2. The dice lattice can be realized with two different schemes: one is to fabricate the trilayer structure of cubic lattice(e.g.,SrTiO3/SrIrO3/SrTiO3)in the(111)direction.[13,14]Alternatively, it is convenient to use the cold atoms in optical lattice.[15–17]Theα–T3lattice is essentially a hybrid between graphene and dice lattice,[18–20]parameterαis used to represent the hopping strength between the hexagonal center and rim atoms.[21–23]Whenαis 0, the lattice becomes graphene, and ifαis 1, it means that the hopping amplitudes between the central atom and one of the hexagonal atoms are equal, then it is the dice lattice. Compared with graphene, the band structure of theα–T3lattice has a distinguishing characteristic. In addition to the conduction band and valence bandE±(k), there is a flat bandE0(k) in the middle,which is similar to that of the dice lattice. For this kind of novel material, researchers have done a lot of works on it, for example, Hofstadter butterfly effect,[27]magnetooptical conductivity,[24–26]Klein tunneling,[28–30]zitterbewegung effect,[31]magnetism,[32,33]magnetoconductivity,[34–36]etc.

The superfluidity of dipolar excitons in double-layerα–T3lattice under strong magnetic field has been studied.[37]Inspired by the superfluid phases for bosons in dice lattice,[38]the superfluidity for fermions inα–T3is studied in this paper. As far as we know, the literature on the superfluid states of fermions in theα–T3lattice is comparatively sparse. It is expected that the dispersionless flat band would play an important role in the formations of superfluid states.In this work,we study the Fermi Hubbard model with attractive interactions inα–T3lattice. In specific, with the mean-field method, we obtain the superfluid order parameters(pairing gaps in superconductor)through solving the self-consistent equations. And then we carefully analyze the evolutions of the superfluid order parameters under the variations of the model parameters. It is found that the Hamiltonian has particle–hole symmetry under certain conditions. Near half-filling, in comparison with the usual two-band system,e.g.,Haldane model,the large density of states of the flat band in theα–T3lattice is in favor of the superfluid states. The superfluid order parameters also show non-monotonic behaviors as the filling factor increases. In addition, there exist some interesting edge states on the boundaries of a lattice ribbon.

The paper is organized as following.In Section 2,we give theα–T3Hubbard model Hamiltonian. The mean-field theory is reviewed briefly in Section 3.In Section 4,we firstly discuss the particle–hole symmetry of the system,and then analyze the superfluid order parameters of theα–T3lattice. In Section 5,we turn to the discussions on the edge states. Finally,we give the summary in Section 6.

2. The α–T3 Hubbard model Hamiltonian

Hubbard model is an important model in condensed matter physics, which can be used to describe metal–insulator transition,[39–41]magnetic phase transition,[42]and superfluid–insulator transition.[43–45]The spatial structure ofα–T3lattice is shown in Fig.1. A unit cell consists of three different lattice sites(A,B,and C),in which sites A and B are located at the vertices of a hexagon to form a honeycomb lattice,and site C is located at the center of the hexagon. The hopping amplitudetAB=t1=tbetween A and B sites. In particular, C sites are only linked to B sites with hopping strengthtBC=t2=αt1withα ≥0. In this paper,we consider two-component Fermi gases with spinσ=↑,↓, which interact through attractive interaction−U(U ＞0). In cold atom experiments,the interactions strengthUcan be tuned by a magnetic field. Theα–T3Hubbard model Hamiltonian reads

withh12(k)=t1∑δcos(k·aδ)+it1∑δsin(k·aδ),h21(k)=h∗12(k),h23(k) =t2∑δcos(k · bδ) + it2∑δsin(k · bδ),h32(k) =h∗23(k), andk= (kx,ky). Specifically, the twodimensional vectorsaδandbδare shown in Fig. 1. In the following, we taket1= 1 as the energy unit. The singleparticle HamiltonianH0has three energy bands, and there exists a flat band in the middle(see Fig.2).

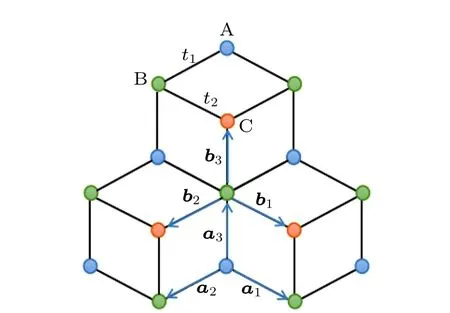
Fig. 1. Schematic diagram of α–T3 lattice. Sublattices A, B, and C are shown in blue,green,and red,respectively. The vectors b1=a1=−1/2], b2 =a2 =/2,−1/2], and b3 =a3 =[0,1] with lattice spacing a=1.

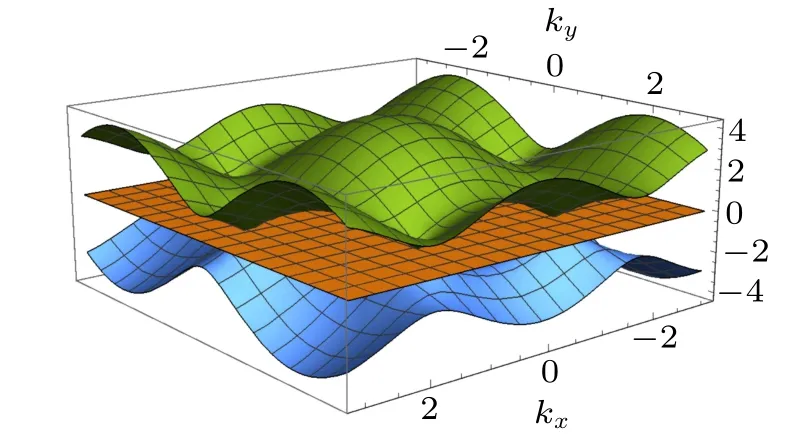
Fig.2. Three single-particle energy bands in α–T3 lattice with t2=t1=1, µ =0, and M =0. The flat band is in middle of upper and lower bands.

3. Mean-field theory

In the presence of the interaction between the opposite spins,we use the mean field decoupling to solve the Hamiltonian and select∆i=−U〈ci↓ci↑〉as the superfluid order parameter (pairing gap). WhenM/=0, the Bogoliubov–de Gennes Hamiltonian in momentum space is

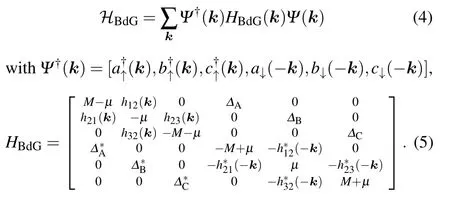
By using the Bogoliubov transformation, the eigenenergiesEp(h)1,2,3(k)can be easily obtained. It is important to emphasize that the BdG Hamiltonian obeys the particle–hole symmetry,p(h)corresponds to the particle(hole)and 1,2,3 represent three branches of excitation due to the sublattices A,B, and C.With the particle–hole symmetry ofHBdG, one can show thatEh1,2,3(k)=−Ep1,2,3(−k),[47]and in the ground state,the thermodynamic potential per unit cell is given by

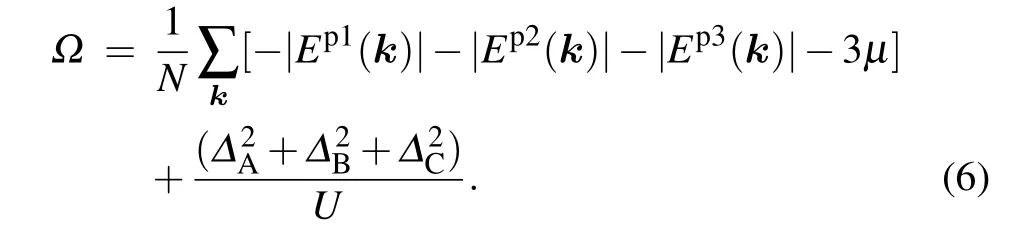
The pairing gaps can be solved by∂Ω/∂∆A,B,C=0, and the chemical potential can be obtained fromn=−∂Ω/∂µ. The resultant four equations for∆A,B,Candµare solved by numerical methods.

4. Particle–hole symmetry and numerical results

First of all, we carefully analyze the particle–hole symmetry (note here that the particle–hole symmetry is different from the one of the BdG Hamiltonian discussed in Section 3)in the case oft2=t1. Applying the particle–hole transformation to the system,[43,48]

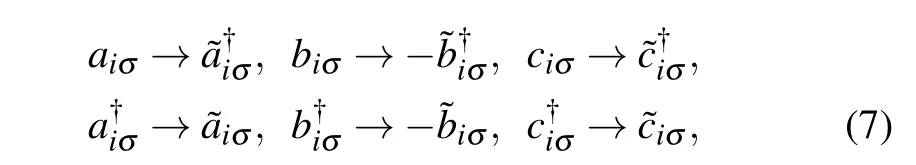
in the case ofM=0 and the chemical potentialµ=0, the Hamiltonian remains invariant at half-filling (3 particles per unit cell).Nevertheless,forM/=0,in order to keep the Hamiltonian unaltered,the inversion transformationr →−rand the exchange of A and C sublattices are needed. In this sense,the Hamiltonian has particle–hole symmetry. In the following,we only consider the case of the number of particlesn ＞3 per unit cell (n=3 is half-filling, i.e., there are three particles in a unit cell). Further more, similar to the Haldane–Hubbard model,[43]one can show that,for the cases of ∆n ≡n−3＞0 and−∆n ＜0,the chemical potential and superfluid order parameters satisfy the relationship

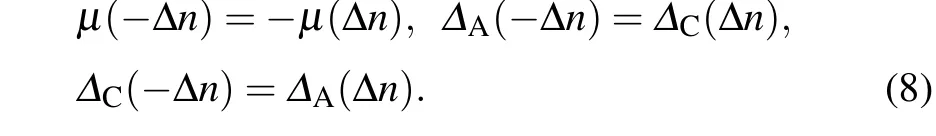
The above equations show that, when it is at the half-filling(∆n=0),the chemical potential is exactly zero and∆A=∆C.

WhenM,t1,andt2take some specific values,it is found that∆A(B,C)are always real. The evolutions of the mean-field superfluid order parameters and chemical potential with attractive interactionUare depicted in Figs.3 and 4.It is shown that,on the whole,∆A(B,C)andµincrease when the interactionUbecomes strong. In contrast with the usual two-band system,for example,Haldane model,the presence of flat band plays an important role in superfluid pairing,especially for half filling.In the Haldane model and at the half filling, when the attractive interaction is weak,the system also remains in an insulator phase. Only when the interaction is large enough,the system develops some non-vanishing superfluid order parameters.[43]While for theα–T3lattice, because of the presence of flat band, when it is half filling, the system is in a metal state.Once the attractive interaction is turned on, the system gets some nonzero superfluid order parameters.

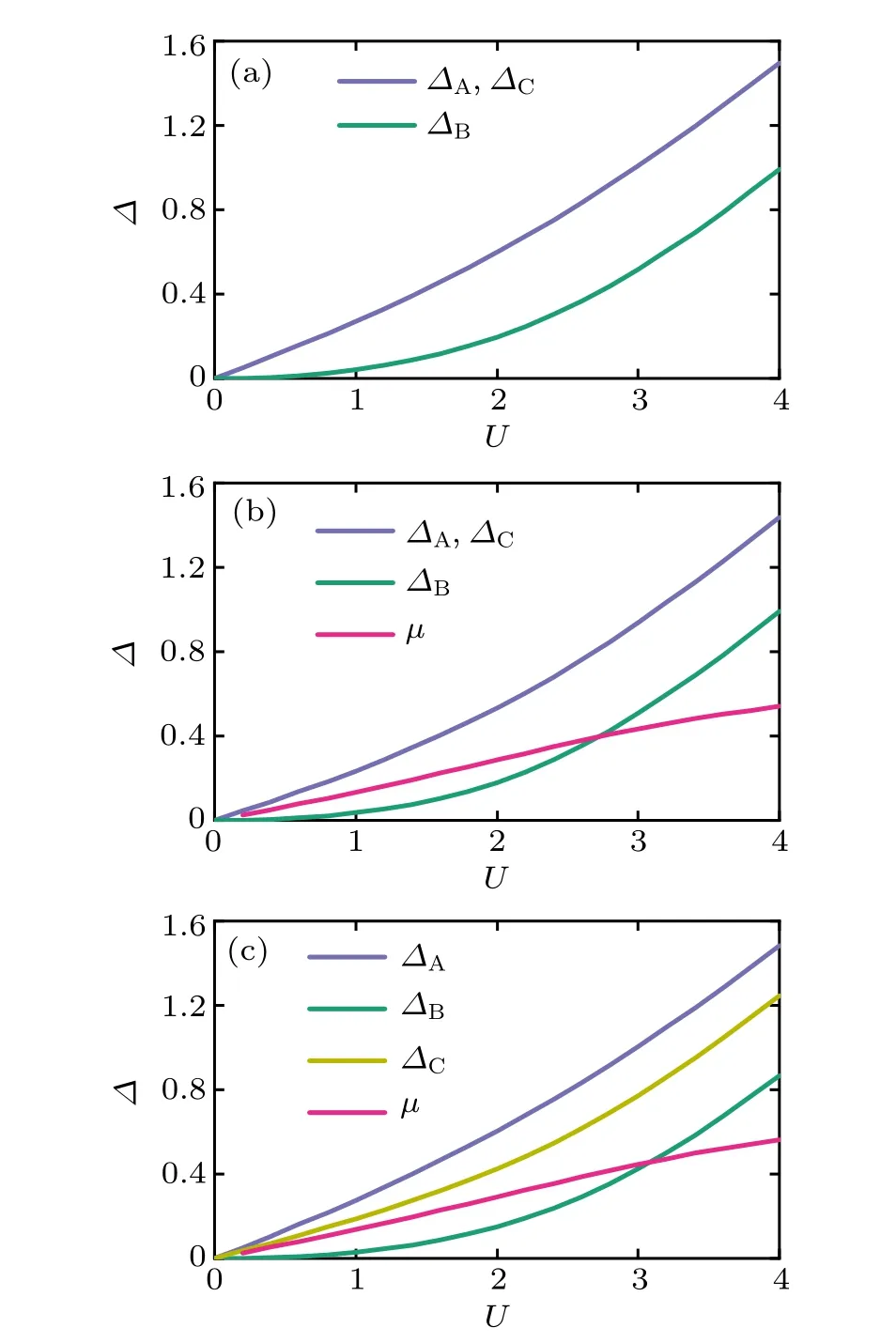
Fig. 3. The superfluid order parameters as functions of interaction U(M=0)(a)at half-filling withµ =0,t1=t2=1;(b)the average number of particles n=3.5,µ /=0 with t2=t1=1;(c)n=3.5,µ /=0 and the hopping amplitude t1=1,t2=1.2.

ForM= 0, the Hamiltonian is subject to the inverse symmetry, there are two different situations: (1) Dice lattice(t2=t1),due to the equivalence between sublattices A and C,whether it is at half-filling or not,∆Ais the same as∆Cbut differs from∆B[Figs. 3(a) and 3(b)], and∆Bis smaller than∆A(C);(2)α–T3lattice(t2/=t1),∆differs for three sublattices A,B,and C[Fig.3(c)]. The∆Clies in between∆Aand∆B.

WhenM/=0, the Hamiltonian does not obey the inversion symmetry and the roles of sublattices A and C are not equivalent. Nevertheless, the Hamiltonian has particle–hole symmetry when it is half-filling andt2=t1. (3) Dice lattice(t1=t2) and at half-filling, the situation of∆A(B,C)is similar as the case (1) discussed above, but∆Bis larger than∆A(C)[Fig. 4(a)]. Here∆A=∆Cis a consequence of the particle–hole symmetry as discussed above. When it is at half-filling,after exchanging sublattices A and C, the Hamiltonian is not changed. Consequently the superfluid order parameters are equal,i.e.,∆A=∆C. (4)Above the half-filling,both dice lattice andα–T3lattice yield three different superfluid order parameters which are similar to case(2). However, for the dice lattice,∆Bis greater than∆Aand∆C[Fig.4(b)]. For theα–T3lattice,∆Cis always the smallest one. When the value ofUis small, there is a little difference between∆Aand∆B. When 3.190＞U ＞0.616,∆Bis greater than∆A, but the situation is reversed atU ≈3.190, and∆Bbecomes smaller than∆A[Fig.4(c)].

In Figs. 5 and 6, we report the evolutions of superfluid order parameter∆and chemical potentialµas the filling factor increases for different interaction strengthU. It is found that, for the whole range of filling 3≤n ≤6, the order parameters increase with the interaction strength. When the filling factor falls into the flat band, i.e., 3＜n ＜4, andM=0,the superfluid order parameters take relatively larger values for a fixed interaction strength (see Fig. 5). This is because the large density of states of the flat band favors the superfluid pairing. When the filling factorncrosses the flat band(n ≥4),the chemical potential displays a jump due to discontinuous of density of states(especially when the interaction is weak) (see Figs. 5(a) and 5(b)). Similarly, the small density of states between the flat band and upper band also causes a dip in the order parameters(see Fig.6). WhenM=0,on the whole,the superfluid order parameters become smaller as the filling factor increases. However,whenM/=0,the superfluid order parameters can reach relatively large values, especially for strong interaction and large filling factor(see Figs.6(c)and 6(d)). When the filling factor approaches its maximum possible value (n=6), the system becomes a band insulator and the superfluid order parameters are vanishing. Figures 5 and 6 also show that the superfluid order parameter for sublattice A is always larger than that of sublattice C,i.e.,∆A＞∆C. In addition,when the inversion symmetry is broken(M/=0),the superfluid order parameters show some nonmonotonic behaviors as the filling factor increases(see Fig.6).

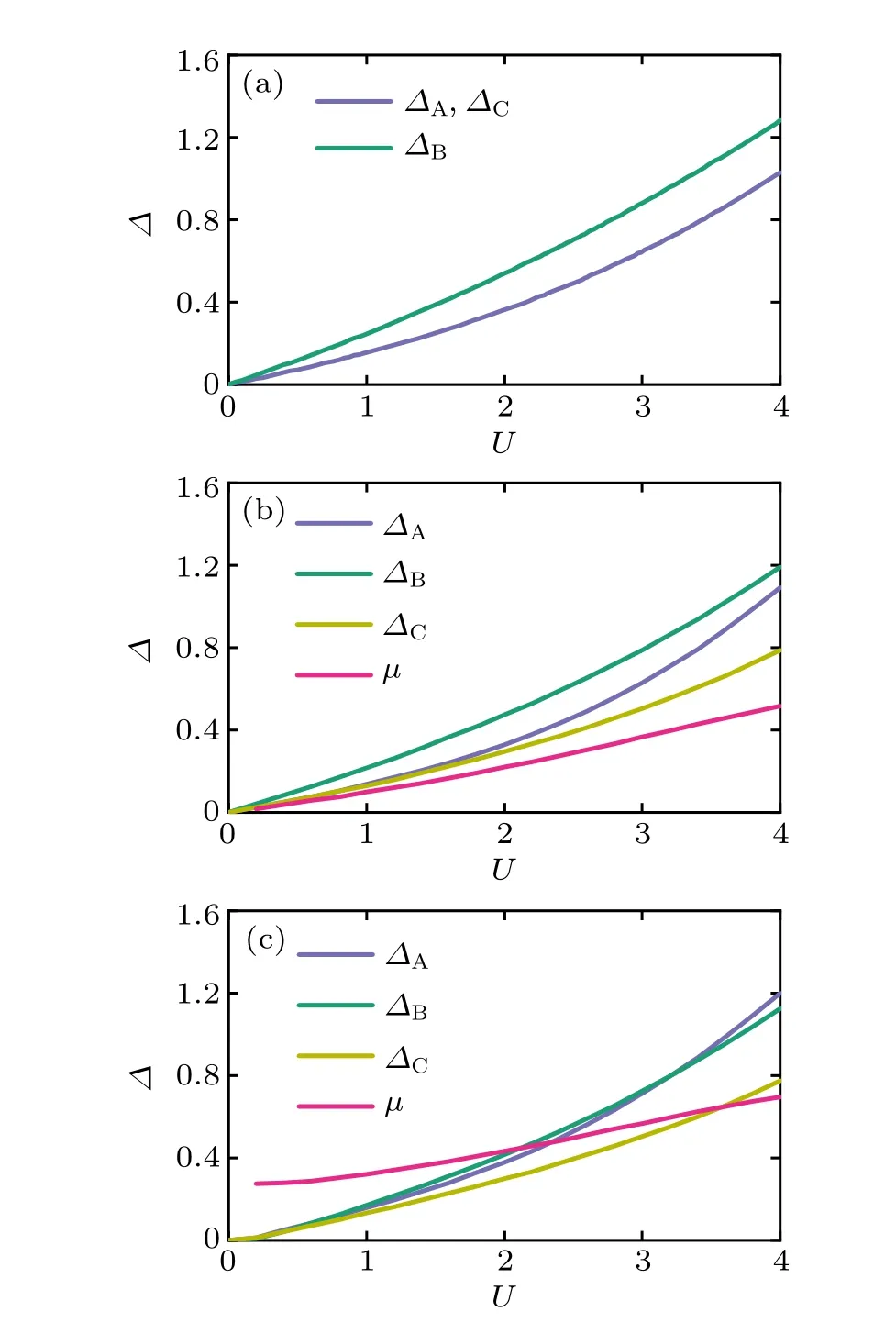
Fig. 4. The evolutions of superfluid order parameters with interaction U (M =2) (a) at half-filling with µ =0, t1 =t2 =1; (b) the average number of particles n=3.5, µ /=0 but t2 =t1 =1; (c)n=3.5, µ /=0 and the hopping amplitude t1=1,t2=1.2.

Fig.5. The evolutions of the superfluid order parameters and chemical potential with filling factor(M=0,t2 =1.2t1 =1.2). (a)Interaction U =1,(b)U =2,(c)U =3,and(d)U =4.

Fig.6. The evolutions of the superfluid order parameters and chemical potential(M=2,t2=1.2t1=1.2. (a)Interaction U =1,(b)U =2,(c)U =3,and(d)U =4.

5. Edge states

In this section, we analyze the edge states of the system under periodic boundary conditions iny-direction and open boundary conditions inx-direction with B–B edges.[26]From left-hand to right-hand side, the lattice sites are arranged like BACBAC···BACB with 20 complete spatial periods.

In the absence of interaction andM=0, there exist two degenerate edge states,[26]and one locates at the left-hand edge, while the other one is on the right-hand edge. WhenM/=0, similarly as gapped graphene case, the existence of edge states can be understood as midgap states near a domain wall.[46,49]Similar as the gapped graphene, the Dirac Hamiltonian(for one of two Dirac cones)of the edge state is

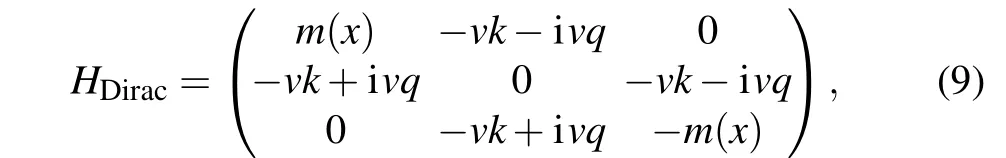
where limx→∞m(x)→M ＞0 and limx→−∞m(x)→−M ＜0.Here Fermi velocityv=3ta/2, momentumkis a real number fory-direction, the momentum operator forx-directionq=−i∂x. The wave function (non-normalized) of the edge state near the left-hand boundary is

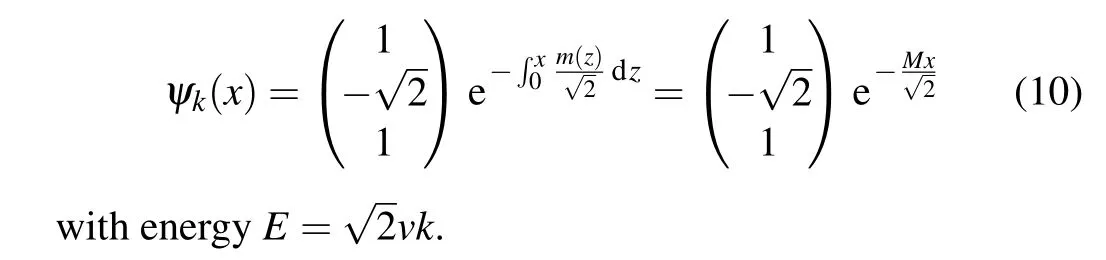
When superfluid order parameters∆/=0, one needs to introduce freedoms for hole’s part to describe the edge states.In such a situation,the wave functions for particle’s and hole’s parts would couple. The edge states are reported in Figs. 7–9. When the Hamiltonian has particle–hole symmetry(n=3,µ=0, andt2=t1), for every lattice momentumk, there also exist two degenerate edge states(not shown in Fig.7),which locate respectively at the left-hand and right-hand boundaries.In such a case, the two edge states are related to each other through a particle–hole symmetry, which includes inversion transformationr →−rand the exchange of A and C sublattices as discussed in Section 4.

When the particle–hole symmetry is broken,for example,the filling is away from half filling(chemical potentialµ/=0)ort2/=t1, the degeneracy of two edge states (energyEi ＞0)is removed(see Figs.7(a)and 7(b)). As the interaction grows(U=0→4),the edge states near the right-hand boundary are pushed into continuous spectra as shown in Figs. 7(b)–7(d).The wave functions of the two edge states Fig.7(a)are shown in Fig. 9 withU=1,M=2,n=3.5,t2=1.2t1=1.2, and lattice momentumk=0.

It is found that the edge states are localized near the boundaries.Figure 8 shows the evolutions of energy bands and edge states ast2increases. It is found that,whent2increases,the lowest particle band is getting flat. At the same time,the region of existence of edge states also becomes broader.We note that the energies of the edge states do not cross the zero energy,which is very different from the case of Haldane model.[43]This is because,in theα–T3model,the total Chern number of the lower three hole bands is zero. Therefore, the edge states of zero energy could not be guaranteed to exist in thisα–T3system. While the Chern number is not vanishing in Haldane model for the topological superfluid phase,which supports two edge states of zero energy.

Fig.7. Energy spectrum and edge states for M=2,t2=1.2t1=1.2,n=3.5. (a)U =1,(b)U =2,(c)U =3,(d)U =4. The edge modes in(a)–(d)are plotted in red.

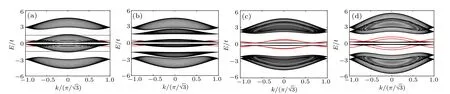
Fig.8. Energy spectrum and edge states for M=2,t1=1,n=3.5,U =1. (a)t2=0,(b)t2=0.4,(c)t2=0.8,(d)t2=1.2. The edge modes in(a)–(d)are plotted in red.

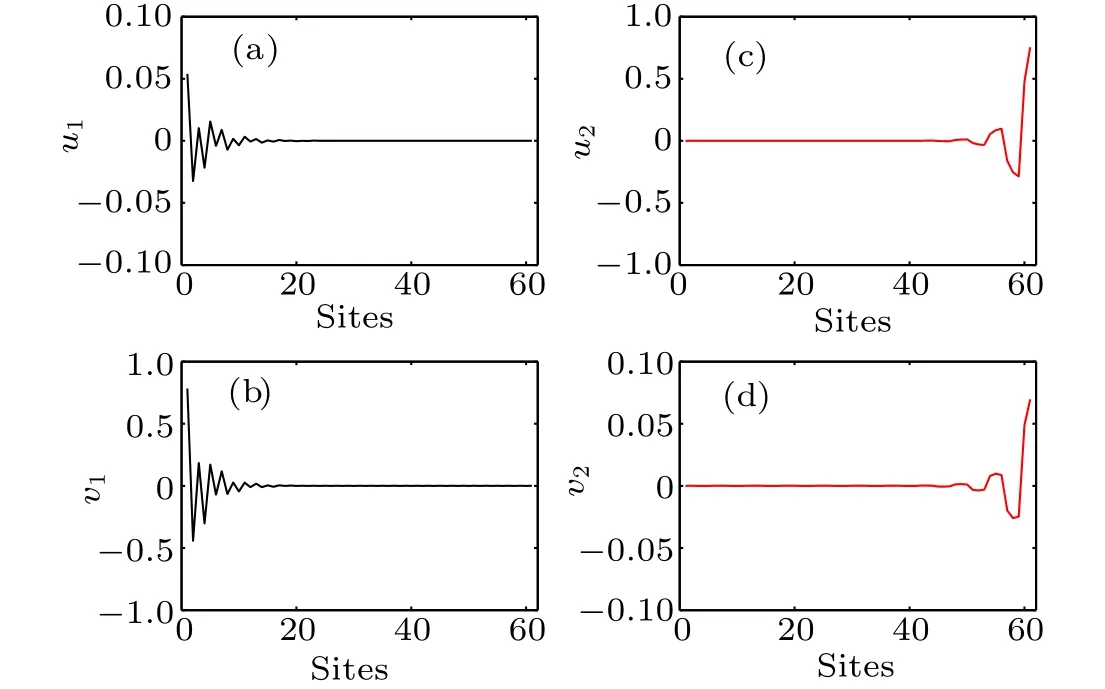
Fig.9. Wave functions of two edge states(energy Ei ＞0)in Fig.7(a)with U=1,M=2,t2=1.2t1=1.2,n=3.5,and momentum k=0(see the red lines in Fig. 7). ui (vi) is wave function for the particle (hole)part of the i-th edge state.

6. Summary

In conclusion, we investigate the superfluid states in attractive Hubbard model ofα–T3lattice. Because there exist three bands, one needs three superfluid order parameters to describe the superfluid states, which is very different from the usual two-band system, e.g., Haldane model or graphene.However,similarly as the Haldane model,theα–T3model also has particle–hole symmetry when two hopping amplitudes are equal. It is found that the flat band plays an important role in pairing, especially for the half-filling. We carefully analyze the the evolutions of the superfluid order parameters with the increase of interaction strength and filling factor. In the absence of inversion symmetry, the superfluid order parameters show nonmonotonic behaviors with the increase of filling factor. Finally,it is found that there exist some edge states localized at boundaries of a ribbon with open boundary conditions.

There are some other interesting questions which are worthwhile to further investigations. For example, what are the collective modes in such a multi-band system,[50–52]how is the superfluid density affected by the flat band,[53–55]and how does magnetic field affect the superfluid states.

Acknowledgement

We would like to thank Jun-Feng Liu and Wen-Yu Shan for useful discussions.