Practical decoy-state BB84 quantum key distribution with quantum memory∗

Xian-Ke Li(李咸柯) Xiao-Qian Song(宋小谦) Qi-Wei Guo(郭其伟)Xing-Yu Zhou(周星宇) and Qin Wang(王琴)

1Institute of Quantum Information and Technology,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

2Broadband Wireless Communication and Sensor Network Technology,Key Laboratory of Ministry of Education,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

3Telecommunication and Networks National Engineering Research Center,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

Keywords: quantum key distribution,quantum communication,quantum memory,decoy state

1. Introduction

Quantum key distribution (QKD)[1]can generate secure keys between two distant users (usually named as Alice and Bob), despite the presence of an eavesdropper (Eve), which has made remarkable progress since 1984.[2–6]Generally,the performance of QKD deteriorates with the increase of transmission distance. To improve the performance of QKD,quantum memory(QM)which has capability of receiving,storing,and retrieving photons,can be applied in QKD systems.[7]

Despite the technology of QM is not mature yet, the characteristics of QM have been greatly improved, such as long storage times,[8,9]high fidelities,[10–12]and high storage efficiencies.[13]More importantly, QM can work at room temperature,[14–16]which makes it more applicable than before. Recently, works on QKD with QM have been reported.[7,17]The authors in Ref.[7]adopted heralded QMs to enhance the performance of measurement-device-independent QKD(MDI-QKD),[18]while the authors in Ref.[17]utilized a portable QM to realize free-space QKD.

In this paper, we investigate the performance of BB84 QKD with a heralded QM, which does not need entanglement sources and can work with the widely used weak coherent sources (WCS). In order to combat the photon number splitting attacks[19,20]caused by multi-photons in WCS,the decoy-state method[21–24]is applied in our scheme. With practical experimental parameters,we demonstrate that decoystate BB84 QKD with QM can exhibit performance better than that of without QM especially in long distance range.

2. Theory and security analysis of BB84 QKD with QM

The QM can be used to receive, store and retrieve photons. According to Ref.[25],we denote the writing efficiency asηin, which is the probability that the pulse sent by Alice is stored in the QM.Alice and Bob know whether the pulse is stored or not,because the QM is supposed to send out a heralding signal when a photon state is successfully stored.[26–28]ηoutrepresents retrieving probability of a pulse from the QM.

In our scheme (Fig. 1), Alice sends a sequence of encoded BB84 states to Bob. At Bob’s side, the QM stores Alice’s pulses with probabilityηin, and reads out the stored pulses with probabilityηout. In the present quantum key distribution systems,in order to reduce the dark count rate,Bob’s single-photon detectors usually work with a gating mode,i.e.,they only open when there is triggering signal. Usually Bob’s single-photon detectors are triggered by the synchronization signal of laser pulses,i.e.,the gating repetition rate is the same as the laser. Considering the heralding characteristic of the QM, Bob can discard those recording events without being heralded,i.e.,the photon pulses are not successfully stored in QM,resulting in substantially reduced dark count rate at Bob’s side.

Fig.1. Scheme of BB84 QKD with a heralded QM.EM:encoding module;DM:detection module.

Letηbdenote the transmittance in Bob’s side, which includes the internal transmittance of optical components and detector efficiency. Andηbcan be boiled down to the channel transmittance.[29]Hence, the overall transmittance between Alice and Bob,η,can be expressed as

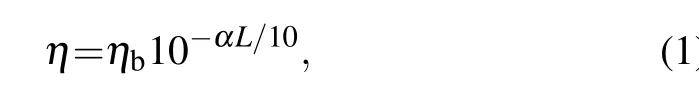
whereαdenotes the channel loss coefficient,andLis the fiber length.

In the framework of BB84 QKD with QM,ηn|mrepresents the transmittance of ann-photon state given that Alice sends anm-photon state before QM.Yn|mandη＇n|mrespectively represent the yield and transmittance at Bob’s side given that the QM successfully stores and retrieves ann-photon state when Alice sends anm-photon state. AndYn|mmainly comes from two parts,one coming from the detector dark count rate,the other from the detection of true signal. The combination gives

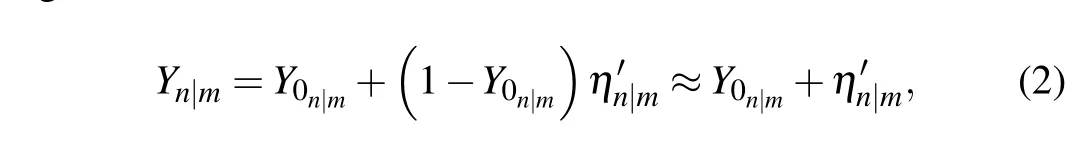
whereY0n|mrepresents the conditional probability of a detection event at Bob’s side given that the QM successfully stores ann-photon state but fails to retrieve it when Alice sends anm-photon state,i.e.,

Note that, due to the assumption that the QM is heralded,there will be no heralding signal if the QM stores no photons.Hence,we havem ≥n ＞0 in Eqs.(2)–(5).

According to Eqs.(2)–(4)and Ref.[24],we have the error rateen|m

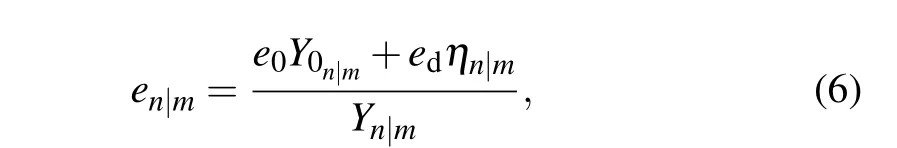
whereedis the probability that a photon hits a wrong detector,ande0is the error rate of the background.

Combining Eqs.(1)–(6), the corresponding average gainQξand the average quantum bit error rate(QBER)EξQξcan be expressed as

Below let us give brief security analysis for our scheme according to information theory,[30]the lower bound of secure key rate of QKD system is equal to the mutual information between Alice and BobI(A:B) minus the mutual information between Eve and Bob(Alice)I(B:E)(I(A:E)),that is

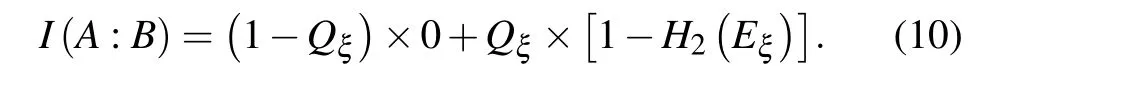
Considering that the error correction efficiencyfis slightly bigger than one, andQ1|1=Y1|1Pξ1, this formula can be modified as

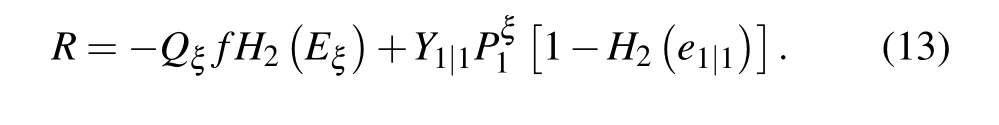
From the above security analysis, we now obtain the lower bound of secure key rate for the asymptotic case.

3. The three-intensity decoy-state BB84 protocol with QM

To implement the scheme of BB84 QKD with a heralded QM, we employ the three-intensity decoy-state method,[24]where Alice randomly modulates the WCS pulses into three different intensitiesu,v,and 0(u ＞v ＞0).

Similar to Eq.(7),the gains of these two decoy states are given by

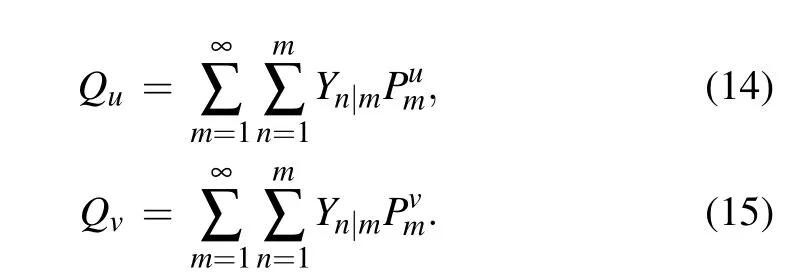
When anym ≥2, them-photon probability of WCS satisfies

4. Numerical simulations

In practical QKD systems, statistical fluctuations have to be considered. Here for simplicity, we assume the channel fluctuation satisfies a Gaussian distribution, and we adopt the Gaussian analysis method to estimate the channel parameters.[32]Here the number of standard deviations in Gaussian approximation analysis method is reasonably set as 6.4, corresponding to a failure probability of 10−10. We simulate all results in this section based on the experimental parameters listed in Table 1.

Table 1. Simulation parameters for decoy-state BB84 QKD with and without the heralded QM.

First, considering differentηinandηout, we investigate the performance of decoy-state BB84 QKD with the heralded QM. For comparison purpose, we also investigate the performance of decoy-state BB84 QKD without QM. Here for simplicity, we assumeηinandηoutwith the same value,i.e.,ηQM=ηin=ηout. Moreover, considering the storage efficiency of the state-of-art quantum memory can reached 92%,[9]we reasonable setηQM= 1,0.8,0.5 in our simulations, corresponding simulation results are shown in Fig. 2.As shown in Fig.2,with reasonableηQM＜1,[9,33]the performance of BB84 with QM is slightly worse than that of without QM in short distance range; However, due to the heralding feature of QM,which can reduce the valid dark count rate of Bob’s single photon detectors,the performance of BB84 QKD with QM is obviously better than that of BB84 without QM in long distance range.

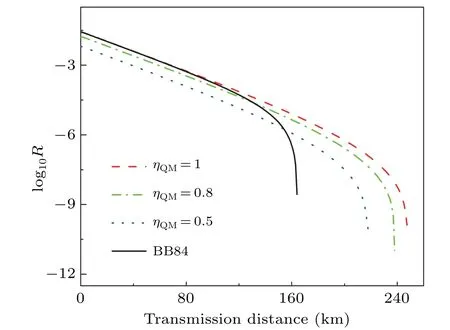
Fig.2. Comparison between decoy-state BB84 QKD with and without QM.

Then, we study the effect of statistical fluctuations on decoy-state BB84 QKD with and without QM, and corresponding results are shown in Fig.3. From Fig.3,we can see that the performance of BB84 with and without QM degrades with the decrease of the total number of pulsesN. However,due to the reduce of valid dark count rate by QM,the performance of BB84 with QM is still better than that of without QM.

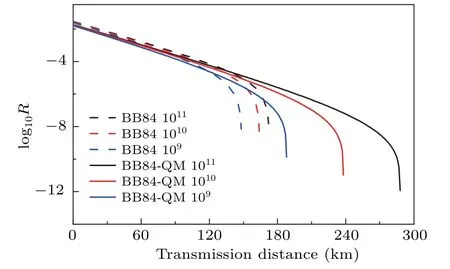
Fig.3. Statistical fluctuations on decoy-state BB84 QKD without QM and with QM.Here,we reasonably set ηQM as 0.8.

5. Conclusion

In conclusion, we have investigated the performance of decoy-state BB84 QKD with a heralded QM.Due to the mitigation of the valid dark counts of Bob’s single photon detectors, the transmission distance of decoy-state BB84 QKD can be greatly extended,which shows the feasibility of adopting QM in practical QKD systems. Furthermore, our present method can also be extended to the measurement-deviceindependent quantum key distribution (MDI-QKD) protocol,and it could show even more interesting characteristics. We believe our work will provide a valuable reference for researchers both in QKD and QM.

Acknowledgment

We thank Dr.Chun-Mei Zhang and Mr.Chen-Chen Mao for useful discussions.