基于改进深度强化学习的虚拟网络功能部署优化算法

唐 伦 贺兰钦* 连沁怡 谭 颀

1 引言

近年来，网络功能虚拟化技术作为网络服务提供的一个重要范式转变，受到了业界和学术界广泛的关注，在网络功能虚拟化 (Network Function Virtualization， NFV)架构下，一系列虚拟网络功能 (Virtual Network Function， VNF)按照特定的顺序构成的服务功能链(Service Function Chain，SFC)为用户提供服务[1]，相同类型的VNF可以部署或者重新实例化在不同通用服务器上，不需要重新购买硬件。

在网络功能虚拟化/软件定义网络 (Network Function Virtualization/Software Defined Network， NFV/SDN)架构下，VNF部署需要解决问题的关键是如何在有限的物理资源中选择满足服务需求的物理通用服务器和物理链路进行部署，在保证网络性能的同时，最大化资源利用率[2]。

目前，已有大量工作对VNF部署机制展开了研究，其中，文献[3]在保证用户服务质量(Quality of Service， QoS)的同时，减少运营商的成本，但是它采用的是静态VNF部署策略，由于网络环境是动态变化的，需要考虑长时间的优化，文献[4]在SFC部署的时候，以最小化SFC端到端时延为目标，通过减少SFC传输时延和处理时延达到减少SFC端到端时延的目的，但是没有关注到物理网络资源利用率的情况，在文献[5]中，在考虑服务器资源容量和流速率的同时，平衡VNF的操作成本、维护VNF实例成本以及VNF部署成本，但是没有考虑SFC时延，进而忽略了用户的QoS。

综上所述，在目前研究VNF部署的相关文献中，大多数文献研究都是基于环境状态已知的情况下，没有考虑到环境随时间的动态变化，而且没有考虑到大量的网络业务请求达到，引起业务请求积压，进而影响网络稳定性问题，而且在考虑SFC部署成本的同时，没有保证用户的QoS。本文针对网络服务请求动态到达引起的SFC部署优化问题，提出了一种基于改进深度强化学习的虚拟网络功能部署算法，本文主要贡献有：(1) 将随机优化问题建立为马尔科夫决策过程(Markov Decision Process，MDP)模型，该模型联合优化SFC端到端时延和SFC部署成本，同时受限于每条SFC的端到端时延以及通用服务器CPU资源、物理链路带宽资源约束；(2) 在VNF部署和资源分配的过程中，存在状态空间过大、动作空间维度高、状态转移概率未知等问题，提出了一种基于深度强化学习的VNF智能部署算法，本算法通过神经网络近似最优动作值函数，从而得到近似最优的VNF部署策略和资源分配策略；(3) 针对深度强化学习代理通过ε贪婪算法进行动作探索和利用，造成神经网络学习效率低、收敛速度慢等问题，提出了一种基于值函数差异的动作探索和利用方法，并进一步采用双重经验回放池，解决经验样本利用率低的问题，加速训练神经网络。

2 系统模型

2.1 网络场景

本文采用NFV编排和控制架构[6]，如图1所示，主要分为3层。

2.2 网络模型

2.2.1 物理网络

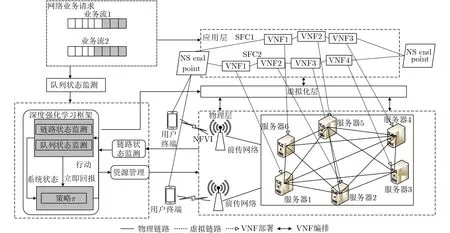
图1 系统模型

2.2.4 SFC部署成本模型

2.2.3 SFC时延模型

2.3 优化目标

本文主要考虑的问题是：在保证用户时延的同时最小化SFC的部署成本，并将物理通用服务器的CPU资源、物理链路带宽资源以及SFC端到端时延作为约束条件，设计了一个效用函数U(t)，将其定义为

该优化目标受到C1～C6限制条件约束，保证优化目标的有效性。C1用于保证虚拟网络中每个VNF只能选择一个服务器进行映射。C2确保每台通用服务器分配给映射在其上的VNF CPU资源之和不能超过该通用服务器的CPU容量。C3用于保证通用服务器的资源利用率，即每台通用服务器的剩余CPU资源低于阈值，否则将不会使用，进一步达到节能的效果。C4表示映射到某条物理链路上的所有虚拟链路数据量之和不能超过该物理链路的总带宽资源。C5用于保证每条SFC的队列长度不溢出。C6用于保证每条SFC在任何时隙都要满足时延要求。C7表示VNF映射的二进制变量。

本文将该随机优化问题转化成一个MDP模型，主要包含状态空间、动作空间和回报函数。

设状态空间为 X，且定义x(t)表示网络在时隙t时的状态，由每条SFC的队列状态，物理链路带宽剩余资源和通用服务器剩余CPU资源构成，其表达式为

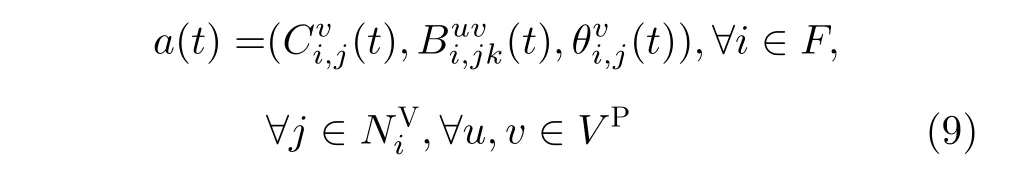
值得注意的是，动作空间需要满足式(7)中的约束C1～C6。

在网络状态x(t)采取动作a(t)后，网络环境会得到即时奖励r(x(t)，a(t))，本文的奖励为效用函数，则r(x(t)，a(t))定义为

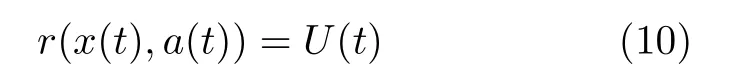
设网络初始状态x(0)的动作策略为π ，即π :x →a，具体表示为

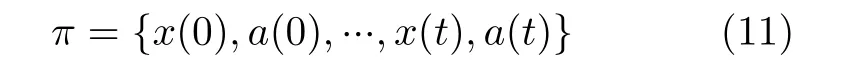
通常最优策略 π*是通过动作值函数Qπ(x，a)得到的，即

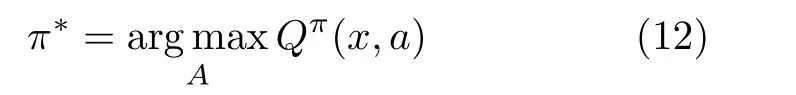
动作值函数Qπ(x(t)，a(t))是用来评判当前状态为x(t)时选择行为a(t)的好坏，可以通过贝尔曼方程迭代获得，即

其中，γ ∈(0，1)表示折扣因子。

则最优动作值函数Q*(x(t)，a(t))可以表示为

最优动作值函数Q*(x(t)，a(t))对应着当前状态x(t)下采取的最优动作a*(t)，将其表示为

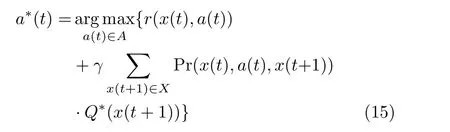
3 基于改进深度强化学习的VNF部署算法

由式(15)知，当获取到每时隙状态的最优值函数，便可得到状态对应的最优动作，且每时隙的最优动作就构成了最优策略π *，由于本文中数据包的到达是随机的，状态转移概率很难获知，因此无法使用值迭代的方式进行求解，同时，传统的基于模型的优化方法通常要作一些假设，存在一定的局限性。根据式(7)，本文的关键问题是确定待VNF部署的目标服务器和资源分配策略，文献[10]中的Q学习算法可以用来直接解决上述问题，但是本文的状态空间和动作空间都是连续值集合，Q学习算法面临维度灾、收敛速度慢等问题。本文接下来提出一种基于改进深度确定性策略梯度(Deep Deterministic Policy Gradient， DDPG)的虚拟网络功能在线部署算法，该算法通过神经网络近似动作值函数，解决维度灾的问题，并且通过基于探索的值函数差异(Value-Difference Based Exploration， VDBE)方法[11]扩展ε贪婪策略，平衡代理在动作选取时的探索和利用问题，进一步针对传统深度强化学习算法从经验回放池中抽取训练样本利用效率低的问题，设置了双重经验回放池，加速神经网络的训练速度。改进的深度强化学习算法框架如图2所示。

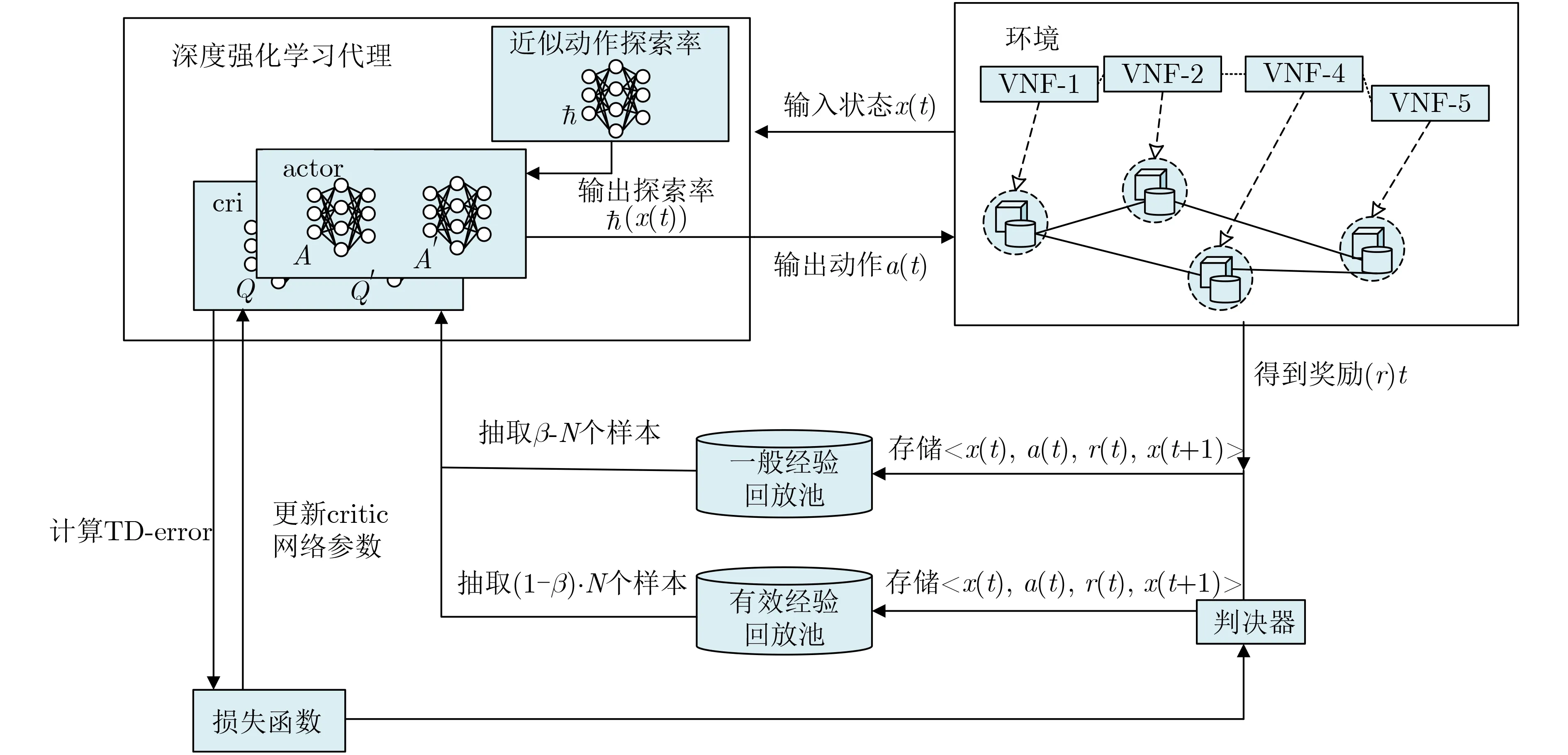
图2 改进深度强化学习算法框架

在该算法框架中，式(14)中Q*(x(t)，a(t))的值是通过critic网络中估计Q网络近似得到，即

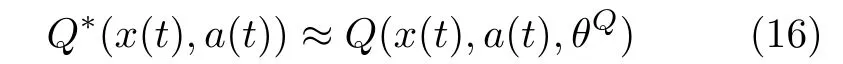
其中， θQ表示估计Q网络的权重，a(t)是通过actor网络输出得到的。

critic网络中的TD-error定义为

进一步，估计Q网络的损失函数就可以表示为

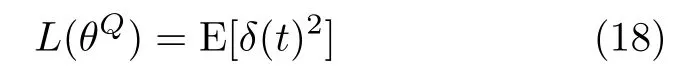
当从经验回放池中抽取 N个样本时，损失函数就变为

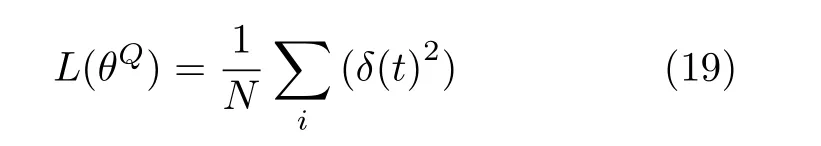
然后采用随机梯度下降算法对估计Q网络的参数进行更新。

actor网络的作用是得到一个确定性策略π(x，θμ)，其中θμ表示估计actor网络的权重，等到神经网络参数训练完成之后，就可以得到近似最优策略，即

其中，Q(x(t)，a(t)，θQ)是通过估计Q网络得到的。

在经验回放池抽取 N个样本后，策略梯度可以转化为

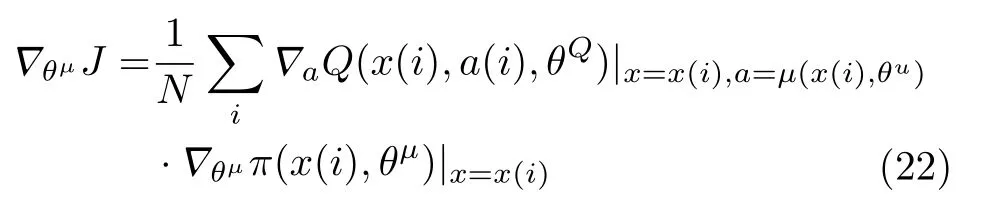
最后，为了探索最优动作，筛选出更好的策略问题，引入随机噪声，从而获得动作，即

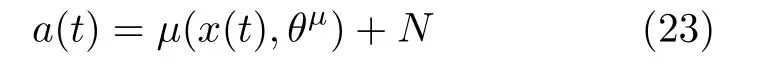
其中， N表示随机过程。

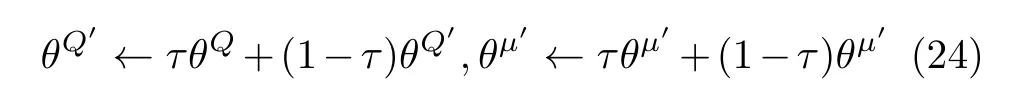
其中， σ表示一个正数，称为反向灵敏度，σ 的值越小，探索概率就越大，δ ∈[0，1)表示所选动作对探索概率的影响参数，通常δ的值为当前状态下可以采取动作总数的倒数[11]，即δ =1/|A(x)|。

在深度强化学习代理开始训练的时候，通常将h(x(0))设置为1。另外，由于本文的状态空间过大，因此本文采用深度神经网络去近似h(x(t))的值，然后将该深度神经网络定义为ℏ 网络。

该神经网络的输入为状态(x(t))，输出为ˆh(x(t))，即

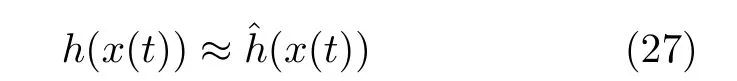
该神经网络的参数通过最小化损失函数L(w)进行训练，表示为

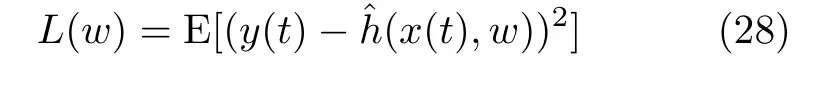
其中， w表示网络的权重，y(t)表示目标值，将其表示为

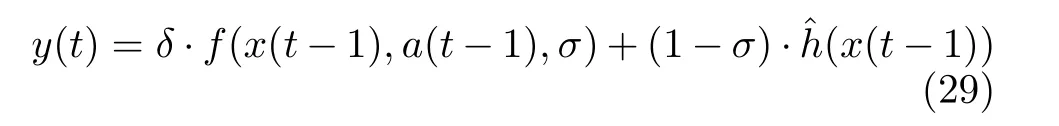
从经验回放池抽取 N个样本后，h 网络的损失函数通过式(27)计算得到

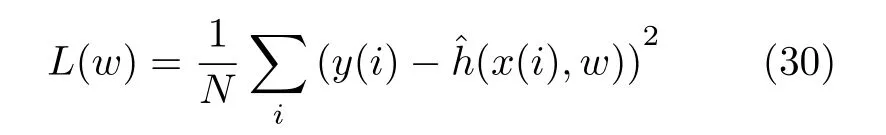
最后采用随机梯度下降算法对 h网络参数w 进行更新。

另外，由于传统的深度强化学习算法对经验回放池的样本是随机采样，有些无用的样本被重复使用，导致样本的利用率低下，于是本文提出双重经验回放池架构，利用TD-error的值来区分样本的好坏，当TD-error的绝对值很大的，δ(t)＞Λ，其中， Λ表示一个正数，说明当前样本对神经网络的权重改变大，给神经网络带来的信息量多，在后面的训练过程中，优先选择该样本[12]。于是将这种样本存储到有效经验回放池中，另外，考虑到一般性，防止过拟合的现象发生，同时也需要从所有的样本值进行随机采样，于是在每个时隙，假设深度强化学习代理需要抽取的样本集大小为 N，则从有效经验回放池中抽取(1-γ)·N个样本，从一般经验回放池中抽取γ·N个样本进行训练，其中γ表示权重值。

4 性能仿真与分析

为了评估算法的有效性以及收敛性，本文将SFC端到端时延、SFC部署成本、资源利用率等作为算法评价标准，对所提算法进行仿真验证。为了更好地评估基于改进深度强化学习的VNF在线部署算法的有效性，与文献[13]基于遗传算法(Genetic Algorithm，GA)的VNF部署算法，文献[14]中的DDPG算法以及文献[15]中的深度信念网络-服务功能链 (Deep Q Network-Service Function Chain， DQN-SFC)算法进行了对比，所有仿真实验均在i7 CPU和内存为8 GB的主机上运行，仿真平台主要基于Python 3.6，通过TensorFlow模块对神经网络进行搭建。

4.1 参数设置

本文假设物理网络为全连接网络，其中包括6台物理通用服务器，假设每条SFC由2～5个VNF构成，另外参考文献[9]对相关参数进行设置，具体网络参数如表1所示。

4.2 仿真分析

由于本文数据包的到达是随机的、状态空间大以及VNF部署和资源分配的动作空间维度高，因此采用改进深度强化学习算法去近似状态Q值，得到近似最优的VNF部署和资源分配策略，图3证明了本文所提改进深度强化学习算法收敛性，并且在相同的学习率α=0.0001下，对比DDPG算法，在训练50次的时候，改进深度强化学习算法已经收敛，而DDPG算法大约在训练100次的时候收敛，因此改进的深度强化学习算法能够快速收敛，原因是本文所提算法在DDPG算法基础上，改进动作探索和利用，解决经验池样本利用率低的问题。

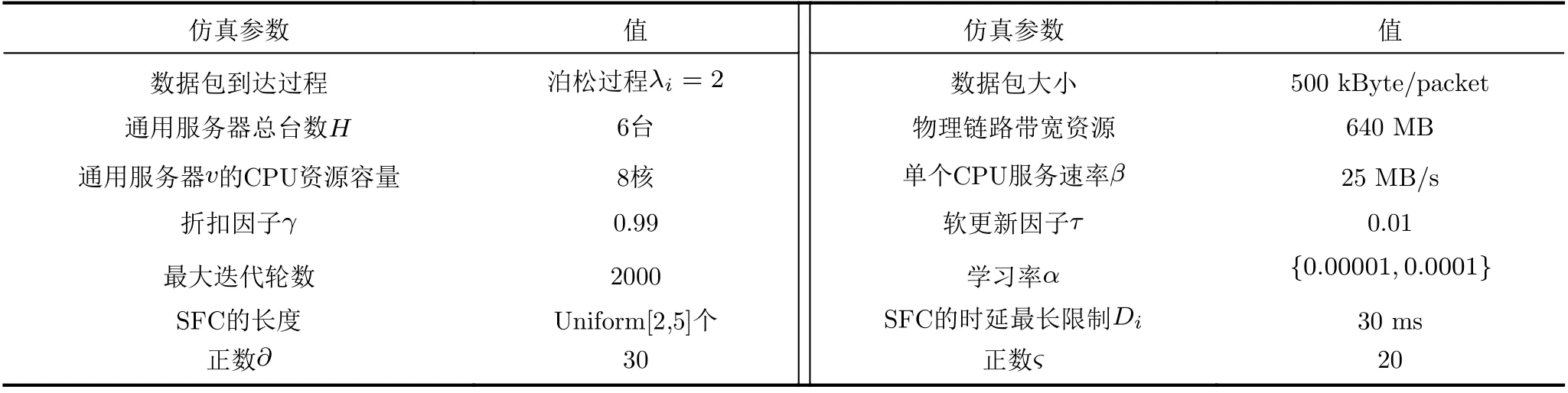
表1 网络场景的仿真参数

图4、图5分别表示在相同的SFC数量下，本文所提基于改进深度强化学习的VNF在线部署算法与其他3种算法在系统总时延和部署成本方面的对比。在此仿真过程中，设置权重值e1，e2都为0.5。

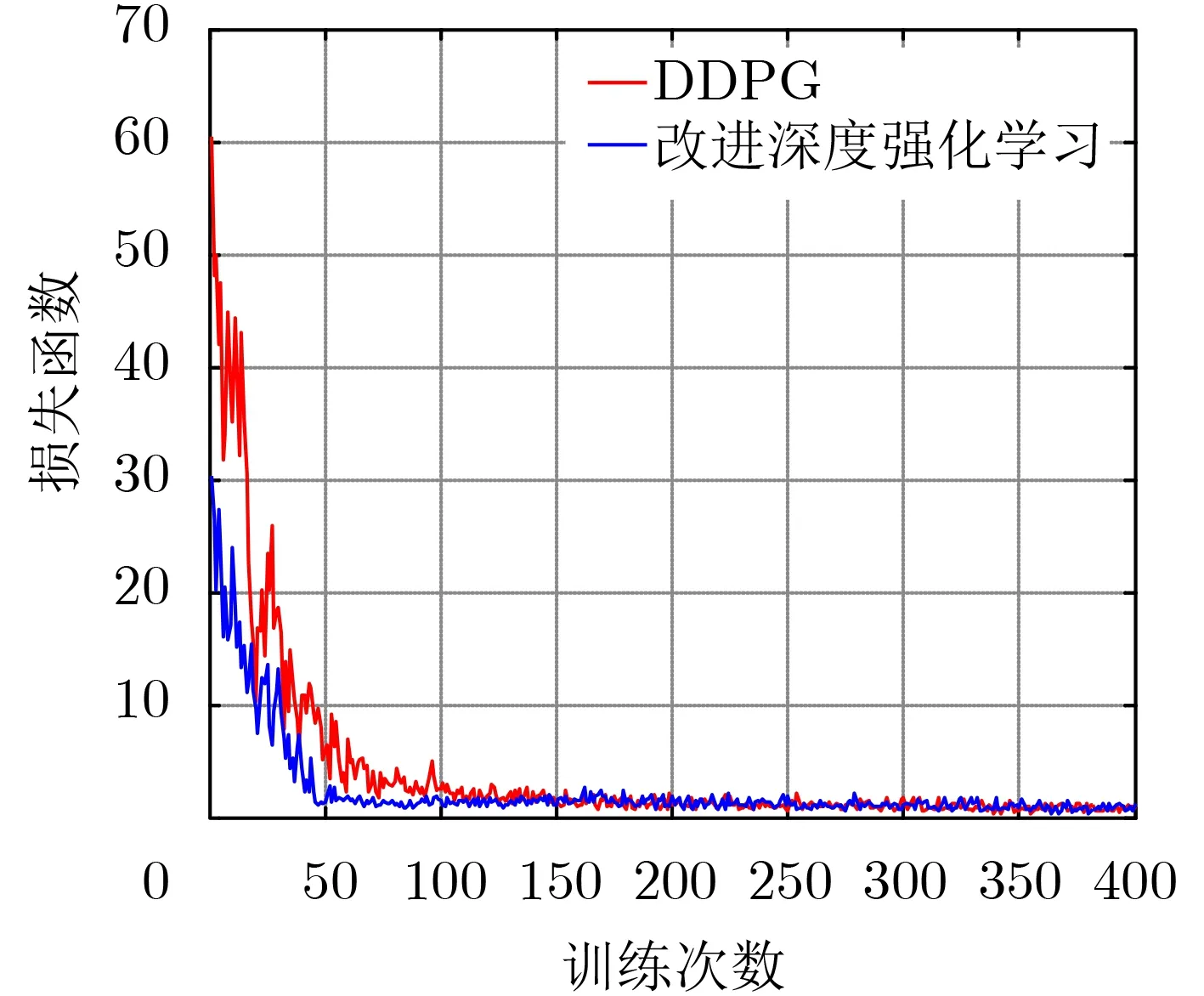
图3 损失函数对比

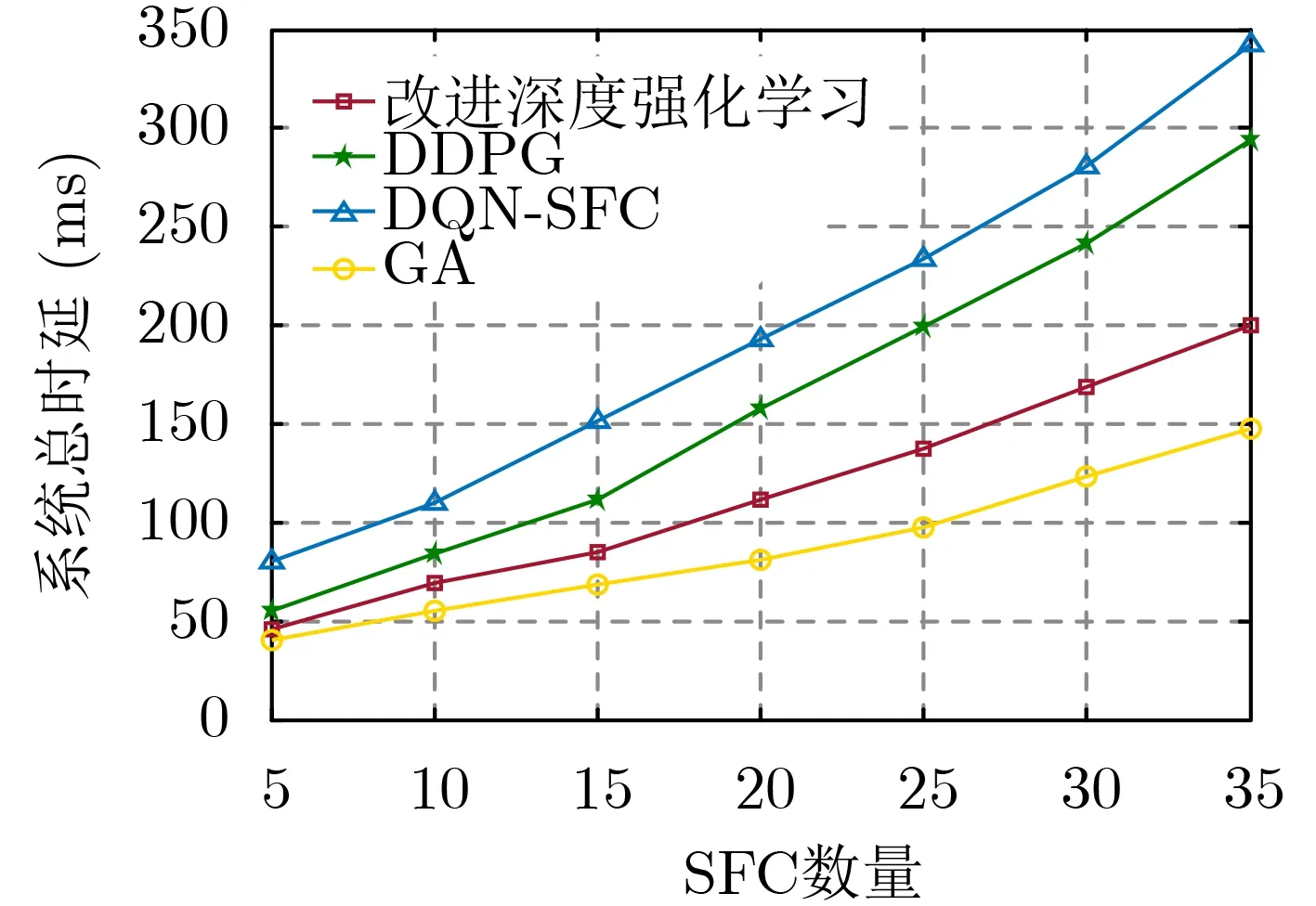
图4 系统总时延对比

从图4、图5可以看出，随着SFC数量的增加，4种算法下的部署成本和系统总时延都将增大，由于GA算法只对时延进行优化，所以它的系统总时延是最低的，但是其没有考虑VNF的部署成本，没有进行合理的资源分配，导致其产生的部署成本是最大的，DQN-SFC算法由于同时优化时延和部署失败产生的运维开销，故它的总时延比GA算法要高，其次，DQN算法适用于解决离散的动作空间，由于本文的动作空间是连续值，故DQNSFC算法在优化时延和VNF部署成本方面明显劣于DDPG算法和改进深度强化学习算法，而且改进深度强化学习算法比DDPG算法在部署成本和系统总时延方面更低，这是因为改进深度强化学习算法在DDPG算法基础上通过状态值函数差异去刻画每时隙动作的探索率，使其能够找到更优的动作，进而获得更好的奖励值，因此改进深度强化学习算法的效用是最大的，如图6所示，由于随SFC数量增加时系统总时延和总部署成本增大，导致效用也会随SFC数量增加而减少，其中，DQN-SFC算法的效用下降最快，而改进深度强化学习中的效用下降最慢。

图5 部署成本对比

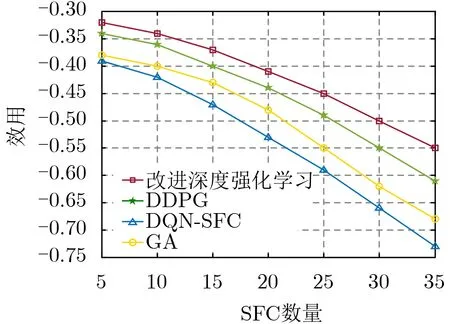
图6 效用对比

5 结论

针对NFV/SDN架构下网络服务请求动态到达引起的VNF部署优化问题，本文首先将随机优化问题建立为一个MDP模型，该模型以最小化SFC部署成本和时延成本为目标，同时受限于每条SFC时延、通用服务器CPU资源以及物理链路带宽资源约束，其次提出一种基于改进深度强化学习的VNF在线部署算法，通过深度神经网络去近似最优的动作状态值函数，从而获得近似最优的VNF部署策略和资源分配策略，最后提出一种基于探索的值函数差异方法去动态地刻画动作探索率，并采用双重经验回放池，解决经验样本利用率低的问题。仿真结果显示，本文所提算法能够加速收敛，并能够优化SFC端到端时延和部署成本。