采用JVC算法生成枝切线的干涉相位解缠方法

王朝霞 刘永信 张 杰 范陈清

①(内蒙古大学计算机学院 呼和浩特 010021)

②(内蒙古大学电子信息工程学院 呼和浩特 010021)

③(自然资源部第一海洋研究所 青岛 266061)

1 引言

3维成像雷达高度计[1，2]综合了传统高度计高精度的测高能力和合成孔径雷达高分辨率的成像能力，使海面高程的面测量成为可能，是遥感技术的最新发展前沿。2016年9月15日，搭载世界首例3维成像雷达高度计的“天宫二号”空间实验室成功发射，在国际上首次实验验证了采用小入射角和短基线干涉测量技术实现宽刈幅海平面高度厘米级精度测量的工作机理。因3维成像高度计测高采用了与干涉合成孔径雷达(Interferometric Synthetic Aperture Radar， InSAR)基本相同的干涉测量技术[1]，故而在高程反演阶段必须通过相位解缠这一环节将滤波后位于主值区间的缠绕相位转换为绝对相位。相位解缠是干涉测量技术的关键环节，解缠的结果将直接影响最终的高程测量精度。在过去的数十年中，许多学者致力于相位解缠算法的研究和改进，但如何在强噪声干扰环境中进一步提升干涉相位解缠的效率和速度，目前仍是一个富有挑战的研究课题。

现有的微波干涉测量相位解缠方法主要有两类，第1类是与展开路径有关的局部法，典型的有枝切法、质量图导引法[3]、最小断点法等；第2类是与展开路径无关的全局法，典型的有最小二乘法[4]、最小费用流法[5]、最小零范数法等。此外，也有综合运用以上两类方法或提出了基于混合数学模型的方法[6]，以在解决实际问题中寻求更好的实验结果。其中，Goldstein等人[7]于1988年在研究In-SAR时提出的枝切法是一种非常经典的算法。该方法通过识别残差点，并根据残差原理设置正确的枝切线，从而选择合适的积分路径，实现相位解缠。但残差原理只是不连续相位存在的充分非必要条件，而且枝切线的放置因方法不同往往结果也不相同，不合理的枝切线放置可能导致相位跳跃和无法解缠的“孤岛问题”[8]。针对枝切法存在的缺点和问题，近年来国内外学者在理论研究和应用中进行了改进。蒋锐等人[9]提出了等效残差点的概念，并基于等效残差点设置枝切线，解决了积分路径穿过残差点密集区所引起的展开相位跳变问题。张妍等人[10]通过虚拟组合残差点改进枝切线算法，在一定程度上解决了残差点较密集区域在放置枝切线时易产生“孤岛”的问题。De Souza等人[11]在获取物体3维轮廓时，利用跳变相位解决了剩余残差点的相位平衡问题，进而通过寻求最小化处理时间实现了动态全息技术中的干涉相位解缠。

本文在研究3维成像高度计高程反演时，提出了一种改进的枝切线干涉相位解缠方法，利用JVC(Jonker-Volgenant-Castanon)全局最优分配算法在正负残差点之间放置枝切线，以进一步缩短枝切线总长度，避免“孤岛”产生，提升干涉相位图中像素的解缠率，降低高程反演误差。

2 相位解缠与Goldstein枝切线算法

由于复数相位的周期性，对配准后两幅相干复图像作复共轭相乘得到的干涉相位图中，相位值是被周期折叠后的相位主值，位于(-π，π]之间，与真实相位值之间相差2 π的整数倍。

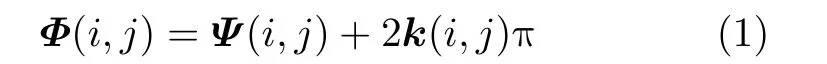
其中，Φ(i，j)为真实相位值，Ψ(i，j)为缠绕相位值，k(i，j)为整数。相位解缠的目标就是恢复被模糊掉的周期分量2k(i，j)π。

一般情况下，干涉相位图的采样率均满足Nyquist原理，因此干涉相位图中相邻像素点之差不超过半个周期，也就是差的绝对值不大于 π。在理想的无噪声环境中，相位解缠只需根据干涉相位图中像素值在距离向和方位向的偏导数进行简单的积分即可。

然而在实际环境中，由于受噪声等诸多因素的影响，干涉相位中存在不连续及不同方向上积分结果不一致的残差点[12](相邻4个像素点组成的正方形回路的相位差积分不为0，而是-2π(负残差)或2π(正残差))。根据相位解缠的基本原则，采用任何一种包含单个或多个正负残差点数不等的积分路径进行解缠，都会产生不一致的结果。

为避免相位解缠后出现不一致的现象，Goldstein枝切线算法首先查找并确定干涉相位图中所有的正负残差点，然后在数量相等的相邻正负残差点之间放置“平衡”枝切线，如果正负残差点数量不等，则把剩余的残差点连接到图像最近的边界上，这样也认为是“平衡”的。进而控制积分路径，使其绕过这些枝切线，采用式(3)进行相位解缠，即可得到一致解缠结果。因所有积分路径包含的正负残差点值总和都为0，所以不会形成全局误差。但同时在枝切线另一侧的像素点将会有相位不连续情况出现。为使不连续像素点数量最小，Goldstein算法在生成枝切线时要求满足总长度最短的原则。此外，在生成枝切线时，在残差点相对密集部分有时形成多条枝切线环绕的像素区域(即“孤岛现象”)，造成被环绕区域像素无法解缠的情况，这些都是改进枝切线算法时需要重点考虑的问题。

3 基于JVC算法生成枝切线的解缠方法

JVC算法[13]是由Jonker， Volgenant和Castanon 3人联合提出的一种全局最优线性分配算法，常用于两个数据点集之间的一对一分配。JVC算法将线性分配问题描述为：在约束条件

成立的前提下，求最小值

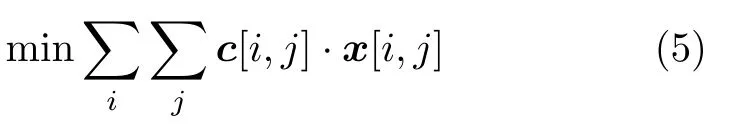
其中，c[i，j]为代价，x[i，j]为权值。

(2) 采用上述基于JVC算法生成枝切线的方法，将残差点分为两类，分别在残差点与其最近边界点之间或正负残差点之间放置枝切线；最后遍历所有的正负残差点，若还有未连接枝切线的，则在其与最近边界点之间放置枝切线，以此确保枝切线的极性平衡。

(3) 在枝切线相对较为稀疏的区域，选取一个非枝切线上的像素点作为起点，绕过所有枝切线采用式(3)的方法进行积分，即可得到解缠相位。

(4) 对于枝切线上未能解缠的像素点，根据解缠后相位图应具有连续性的原理，将枝切线上点的像素值用7×7邻域内已解缠像素点的均值替换，完成全部像素点的相位解缠。

4 方法验证

4.1 3维成像高度计海面仿真干涉相位图验证

为验证算法的可行性和有效性，本文根据“一发双收”天线3维成像高度计的成像原理[1]仿真了Ku波段的海面干涉相位图。首先采用P-M海浪谱和双尺度模型模拟海洋表面，求得海面上每一点的高程数据。然后利用Delaunay三角剖分法将海面划分为三角形小面元，采用物理光学(Physical Optics，PO)模型及其Kirchhoff近似解计算仿真海面区域的后向散射系数。最后根据3维成像雷达高度计的成像原理使用后向投影(Back Projection， BP)算法进行仿真成像，得到两幅仿真3维成像高度计海面相干复图像。经图像配准、去平地效应及滤波后得到如图1(a)所示的干涉相位。

在3维成像高度计海面仿真干涉相位图中提取残差点，共得到正残差点578个，负残差点577个。分别采用本文算法和Goldstein枝切线算法生成枝切线，结果如图1(b)和图1(c)所示。Goldstein枝切线算法生成的枝切线总长度为3313像素，本文算法生成的枝切线总长度为1723像素。

为验证本文算法的可行性和有效性，分别采用Goldstein枝切线算法、四向加权最小二乘法[14]、快速傅里叶变换(Fast Fourier Transform， FFT)算法[15]和本文算法对3维成像高度计海面仿真干涉相位图进行解缠，结果如图2所示。Goldstein枝切线算法的像素解缠率为76.99%，本文算法的像素解缠率为88.03%，采用7×7邻域内的解缠像素均值替换枝切线上点的像素值后，解缠率可达100%。观察解缠后的4幅干涉相位图，可见四向加权最小二乘法解缠后相邻相素之间的连续性在4种算法之中最好，阶跃式跳变最少，本文算法与FFT算法次之，传统Goldstein枝切线算法相对最差。

为定量比较4种算法的解缠结果，利用式(9)分别将解缠相位转换为图3(a)—图3(d)所示的相对数字高程。

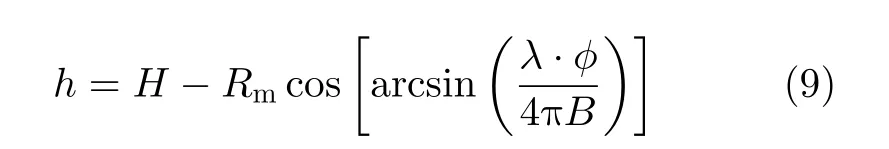
其中，h 为相对数字高程， H为3维成像高度计雷达平台高度(本文取393 km)， Rm为雷达主天线到海面高程点的斜距， λ为电磁波波长，φ 为解缠后的相位值， B为基线长度(本文中取10 m)。

统计图3(a)—图3(d)所示数字高程与图3(e)所示的原始模拟数字高程的均方根误差(Root Mean Square Error， RMSE)，并在同样的软硬件环境(Intel Core i5-4590 4核，16 GB DDR3 1666 MHz内存，Win7 x64旗舰版操作系统)下分析4种算法的时间复杂度及实测运行时间，详细对比结果如表1所示。表中，分析时间复杂度时， M， N分别为干涉相位图的行、列数，m ， n分别为正、负残差点的个数，s=max(m，n)， W为四向加权最小二乘法控制加权窗口的尺寸， I为FFT算法的迭代次数。

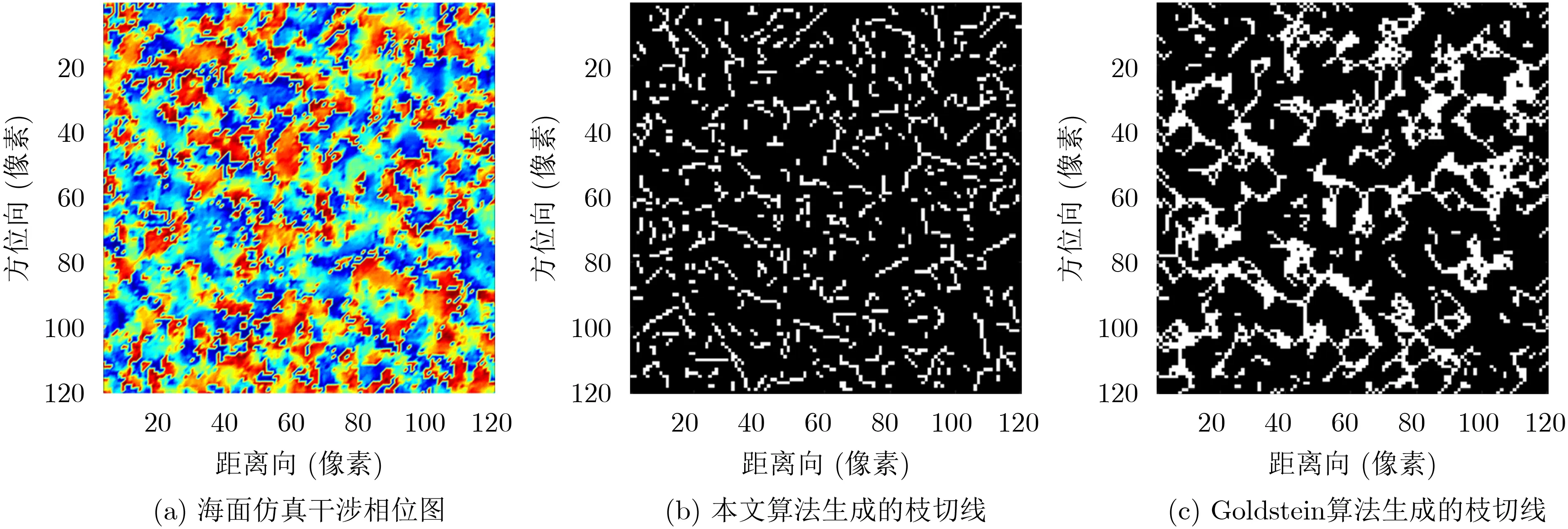
图1 3维成像高度计海面仿真干涉相位及其枝切线示意图

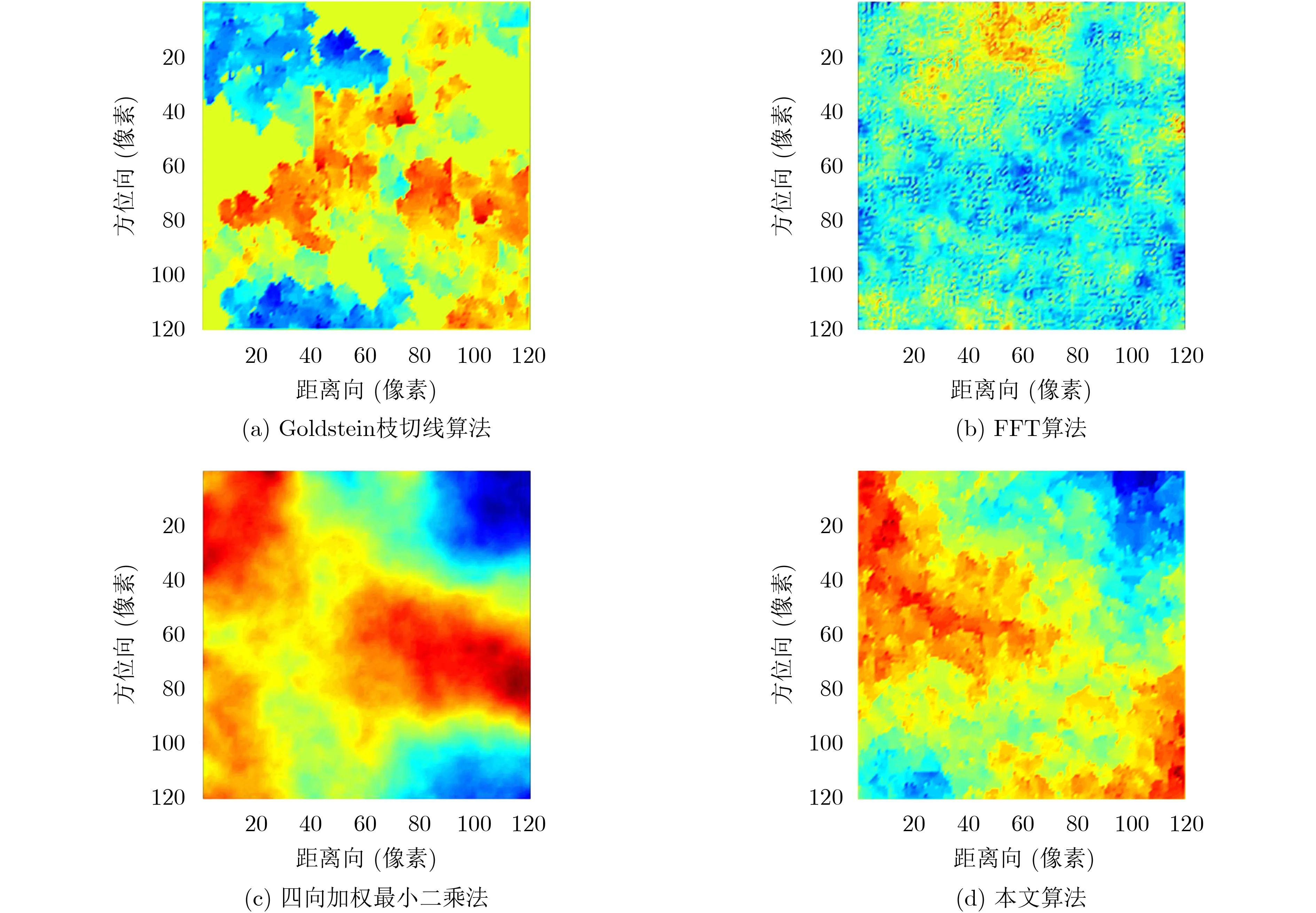
图2 3维成像高度计海面仿真干涉相位解缠结果

由图3及表1可知，虽然四向加权最小二乘法解缠后相位值的连续性和算法运行时间优于其他3种算法，但解缠相位对应的数字高程误差大于本文算法和FFT算法，这是因为四向加权最小二乘法在进行相位值拟合时导致了误差的全局扩散。采用4次迭代FFT算法时，虽然运行时间优于本文算法，但转换后的高程误差约为本文算法的2倍。本文算法的执行时间优于Goldstein枝切线算法、略次于FFT算法，但解缠精度均高于其他3种算法，能够满足3维成像高度计厘米级测高误差的要求。

就时间复杂度而言，本文算法主要取决于残差点的稠密程度，越稀疏时间复杂度越低。当m ＜M， n ＜N ， 1+log2s ＜W2时，本文算法的时间复杂度将会低于其他3种算法；当nlog2s ＞MN时，本文算法的时间复杂度将高于其他3种算法。介于上述两种情况中间时，本文算法的时间复杂度一般低于Goldstein枝切线法，高于四向加权最小二乘法，接近FFT算法。

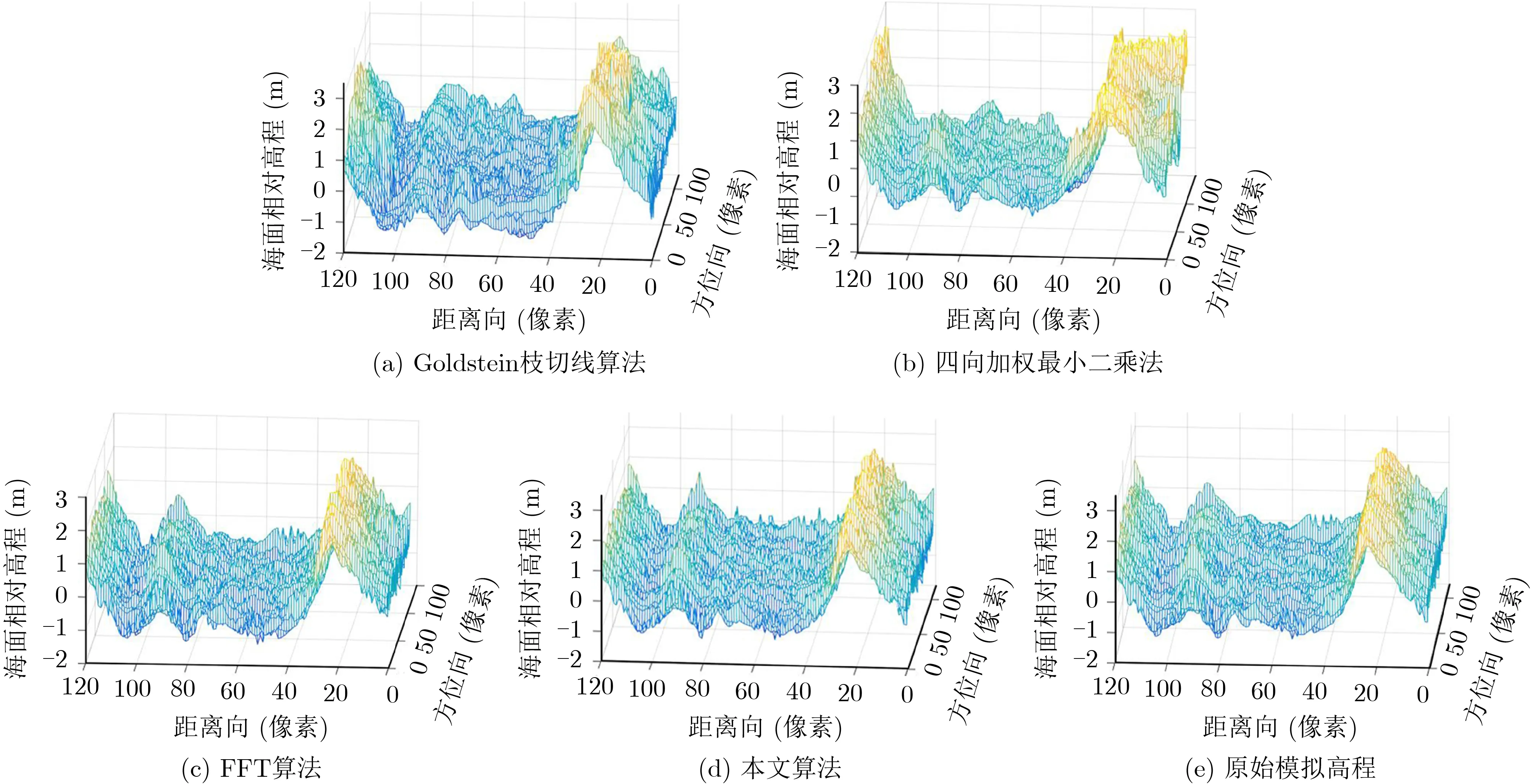
图3 海面仿真干涉相位图解缠后对应的相对数字高程

表1 3维成像高度计海面仿真干涉相位图4种算法解缠结果对比

4.2 实际Etna火山地区干涉相位图验证

为说明算法的通用性和有效性，利用本文算法和Goldstein枝切线算法、四向加权最小二乘法、FFT算法分别对ERS1/2两次经过Etna火山地区时获取的相干SLC(Single Look Complex)数据进行解缠。本文从经过多视处理的两幅复图像中分别选取500像素×500像素的区域进行实验，经配准、去平地效应、滤波后的干涉相位图如图4(a)所示。提取残差点，得到正残差点3383个、负残差点3389个。本文算法和Goldstein枝切线算法生成的枝切线如图4(b)、图4(c)所示，本文算法和Goldstein枝切线算法生成的枝切线长度分别为13546像素和15664像素。解缠后的结果如图5所示。将解缠相位转换为图6(a)—图6(d)所示的相对数字高程，并与图6(e)所示对应经纬度的ASTER GDEMV2 30 m分辨率数字高程数据[16]进行比较，计算RMSE，4种算法的详细对比结果如表2所示(统计算法执行时间的硬件环境与4.1节相同)。

图4 Etna火山地区干涉相位及枝切线示意图

图5 Etna火山地区干涉相位图解缠结果

由图5、图6及表2可知，虽然FFT算法和四向加权最小二乘法两种全局性算法解缠后相位的连续性和执行时间优于本文算法，但解缠后相位所代表的高程走势与原干涉相位图不一致，且与GDEMV2之间的RMSE相对较大，这是由于两种算法均引起了误差的全局性扩散。传统Goldstein枝切线算法解缠虽未改变高程走势，但未解缠相位和相邻像素值之间的阶跃式跳变较多，解缠结果连续性较差，且与GDEMV2的RMSE较大。本文算法兼顾了解缠的精确性和相位连续性，消除了大部分相邻相素之间阶跃式跳变，避免了误差的全局扩散。

分别对比图2(b)、图2(c)与图4(b)、图4(c)中两种算法生成的枝切线，可以看出采用本文算法生成枝切线可以有效防止其相互连接形成“孤岛”，使得干涉相位图中除枝切线以外的像素点都可以通过积分进行解缠。这是因为，不论是与边界点直接相连生成枝切线，还是通过JVC线性分配后在正负残差点对之间放置枝切线，每个残差点只存在于一条枝切线上，任何一条枝切线都是两点之间的连线(忽略像素数字化时取整的因素后可近似为直线段)，是无法连成闭环的。

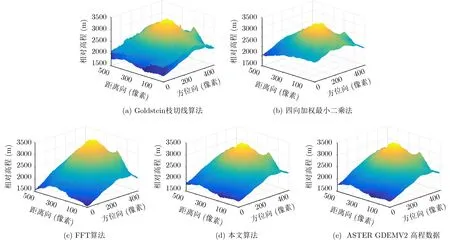
图6 Etna火山地区干涉相位解缠后对应的相对数字高程

表2 Etna火山地区干涉相位图4种算法解缠结果对比

5 结束语

本文为缩短枝切线相位解缠算法中生成枝切线的总长度，提升干涉相位图的解缠率和准确性，提出了采用JVC全局最优线性分配算法在残差点之间放置枝切线，以此对Goldstein枝切线算法进行改进。通过对3维成像高度计海面仿真干涉相位图和Etna火山地区干涉相位图进行解缠实验，结果表明在同样的软硬件运行环境中，本文算法在生成枝切线总长度、像素解缠率和运行时间上均优于Goldstein枝切线法，解缠精度优于Goldstein枝切线法、四向加权最小二乘法和FFT算法，同时能够较为有效地防止“孤岛现象”产生，为干涉相位解缠提供了一种可行的方法。然而，在残差点数量少且正负残差点距离较近的干涉相位图中，对Goldstein枝切线算法的改进并不明显；在信噪比低、残差点密集的干涉相位图(或局部区域)中，算法运行时间相对其他算法较长，且无法完全避免“孤岛现象”的产生，这是下一步需要重点考虑的优化方向。