黄河中上游流域水沙变异关系模型研究

落全富, 包为民, 陈文波, 汪勤海, 孙青雪, 金 樊, 王正华

(1.杭州市水库管理服务中心, 浙江 杭州 311305; 2.河海大学 水文水资源学院, 江苏 南京 210098)

全球气候变化和人类活动影响加剧，导致水文系列均值的变化，使得系列具有不一致性和变异性[1]。特别黄河流域泥沙锐减现象全球瞩目，但其减少原因、成因机理至今罕有深入研究[2]，以致泥沙减少是由气候变化还是水保措施作用所致或各因素的贡献比例多大等问题一直难以解决[3-8]。黄土高原，由于水土保持措施、退耕还林、生态保护等技术与政策措施作用，河流水沙产生了显著变化，水沙变化原因已成为研究热点。目前研究的方法主要有概念水文模型为基础的分类定量评估法、时间系列变化趋势分析法和驱动因素分析法[9-10]。用水文概念性模型对泥沙变化原因进行分类定量评估是研究较早的方法，概念性模型具有的物理成因关系，定量确定影响因素变化与泥沙变化量的关系[11-14]。这类方法的优点是物理成因机理清楚，缺点是要求资料多，实际常难以满足模型要求。如黄河流域泥沙概念模型，涉及超渗产流计算，要求有1 h甚至5 min间隔的时段雨量资料[14-15]，这对于变化原因分析要求有50 a以上的长系列计算，是非常困难的。赵羽西和谢平等的变异分级方法、Mann-Kendall突变检验法、Pettitt法、有序聚类分析法和Bernaola-Galvan分割法是趋势分析法有代表性的成果[1,16-21]。这些方法虽然要求资料较少，但只能分析是否存在变异和确定系列的突变点及变异程度。驱动因素分析法，直接建立影响因素与泥沙变异之间的关系，是近期开始为水流泥沙变异规律研究所重视的。如Wang等[2]根据输沙量(S)等于降雨量(P)、径流系数(a)和含沙量(s)相乘的特殊关系S=Pas，推导了输沙量变化与3者间变化的微分关系：

(1)

该研究开辟了变异规律研究的新途径，但这关系还存在局限性。首先不能用于一般问题的分析中，特别是人类活动因素对泥沙变化的影响不能直接反映；其次含沙量s与输沙量S类似都受降雨、径流系数、人类活动因素的影响；还有径流系数和含沙量已知相当于输沙量已知，所以这两因素同时作为输沙量关系的自变量相当于自己与自己建立关系，是不合适的，通常含沙量不能作为输沙量模型的自变量。为此，本研究从水沙变异影响因素分析入手，研究黄河中上游流域水沙变异与影响因素变异间的物理成因关系，定义了变异变量，推导了以微分为基础的水沙变异关系模型，并用实际水沙系列进行了模拟论证和变化原因定量分析。

1 模型结构研究

水文系列变化通常受气候和人类活动两个层面的因素变化影响，气候因素变化具有周期性，其均值和方差等统计量随周期变化不大，而水文系列变异是指由均值和方差等特征统计量改变的变化。所以，时间系列变异规律和模型研究，首先要考虑如何消除气候周期性变化的影响，使得变异规律突显并简化变异模型结构。

1.1 变异变量定义与公式

要研究泥沙变异规律和构造变异模型，首先要定义变异变量。对于泥沙时间系列的变异或突变点检测等研究问题，变异或突变通常是指均值的变化。对于自然因素的均值变化，通常都是连续变化的，只不过变化速度突然加快，给人感觉产生了突变。因此，可以用一定时期的滑动平均构建变异变量，以消除周期内的气候变化因素影响。

设有时间样本系列x1,x2,x3,…,xL，可以构建向后滑动平均变量B

(2)

式中：T为时间系列变化周期；i表示时间序列；L为序列长度。类似地有向前滑动平均变量F

(3)

反映均值变化的变量V和变异量ΔV计算公式分别为

Vi=(Bi+Fi)/2， ΔVi=Bi-Fi

(4)

由公式(4)所表达的要素变异反映了滑动平均值的变化量，其值的绝对值越大表示变异越剧烈。

流域泥沙变化，影响因素有降雨、水流、植被、水利工程等。研究泥沙变异规律与模型，就是要研究这些类型因素变异与泥沙变异之间的因果关系。根据上述变异变量定义，对下面物理因素量有相应的表达。如泥沙S向后滑动平均变量SB为

(5)

向前滑动平均变量SF

(6)

反映均值变化的变量SV和变异量ΔSV如下

SVi=(SBi+SFi)/2， ΔSVi=SBi-SFi

(7)

其他植被因素C，降雨P，水流Q，水利工程因素W都可以类似地构建。C均值变化为CVi；C变异量为ΔCVi；P均值变化为PVi；P变异量为ΔPVi；Q均值变化为QVi；Q变异量为ΔQVi；W均值变化为WVi；W变异量为ΔWVi。

1.2 变异模型推导

考虑降雨、水流、植被覆盖度和水利工程指标与泥沙的一般关系：

S=f(Q,C,W,P)

(8)

式中：P为降雨量(mm)；Q为流量(m3/s)；C为植被覆盖度,表示植被占流域面积比例；W为水利工程指标,表示水利工程占流域面积比例。

有微分表达

(9)

该微分模型对于任意的泥沙关系都是通用的，关键是不知公式(8)的具体结构，所以无法获得各项偏导数的具体表达函数。根据大量泥沙研究表明[22-26]，通用土壤流失方程是很有效的模型。该模型把土壤侵蚀量表达为：

S=b0Qb1Cb2Wb3Pb4

(10)

式中：b0,b1,b2,b3和b4为常参数。其中S对Q的偏导数据公式(10)可推导得：

(11)

类似地有

(12)

将S对Q，C，W和P求偏导的结果代入公式(9)，得到泥沙与其影响因素的微分模型如下

(13)

将上文定义的变异变量看作是上式中的dS，dQ，dC，dW，dP微分变量，则SV对变量QV，CV，WV，PV的偏导数就可以类似地表达为：

(14)

和

(15)

由此可得泥沙变异与影响因素变异的关系：

(16)

式中：bQ,bC,bW,bP为常系数。类似地可以推导得水流的变异公式：

(17)

式中：cE，cP，cC和cW为常系数； ΔEV为年蒸发变异量，类似地

(18)

公式(15)—(18)就是以微分理论为基础的水沙变异模型。

2 模型检验与结果与分析

2.1 流域特征

本次检验选择了黄河中上游的7个流域，流域特征及测站名称详见表1。这些流域面积变化范围为8 515～682 166 km2，控制黄河流域面积的91%，资料系列较长，普遍在53 a以上，这些流域的模型检验，无论是流域尺度、空间地理位置和资料系列长度考虑，都具有很好的代表性。

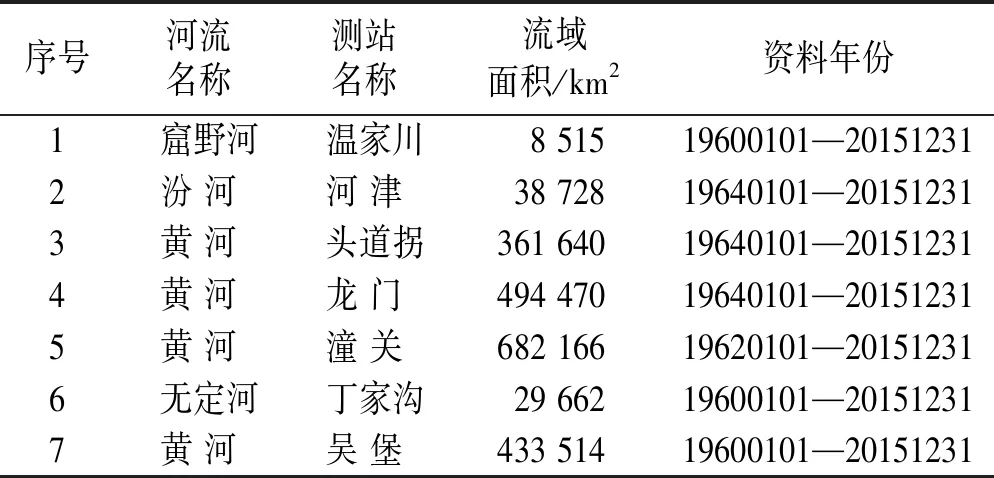
表1 研究流域基本特征

2.2 精度指标

本研究采用的模型计算精度评价指标有有效性系数DC：

(19)

相关系数RR：

RR=

(20)

和绝对相对误差比Re：

(21)

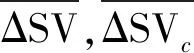
2.3 变异模型结构合理性与模拟有效性分析

2.3.1 模型计算结果 变异模型计算，首先要确定气候周期T。气候变化主要受太阳活动周期影响，太阳活动周期与太阳黑子爆发密切相关，据研究太阳黑子具有11.2 a的周期，所以这里选择滑动平均周期T为11。7个断面流域用最小二乘法确定的参数详见表2，变异模型计算的结果和精度统计详见表3—4及图1—2。表2中SB和SBc是泥沙的观测与模型计算向后滑动平均量，SF和SFc是泥沙的观测与模型计算向前滑动平均量，e是计算量的相对误差，下标s和q分别表示输沙率和流量，如DCs和DCq分别表示输沙率和流量模拟有效系数等。表2中植被覆盖率C为面积比例。用于分析植被变化的遥感数据为GIMMS NDVI和SPOT VGT NDVI两种数据集，其中GIMMS NDVI数据来自于寒区旱区科学数据中心(http:∥westdc.westgis.ac.cn/)提供的NOAA/AVHRR NDVI半月合成数据集，空间分辨率为8 km×8 km，时间跨度为1984年1月至2006年12月。信息的详细提取过程参考文献[27]。根据这些数据确定了植被覆盖率和水面比例的年变化函数

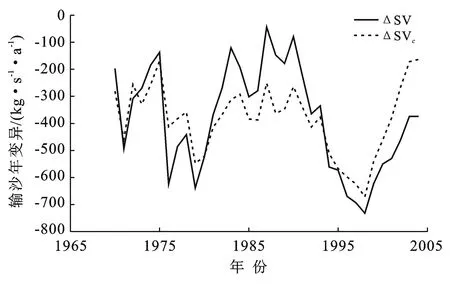
图1 温家川站实际泥沙年变异ΔSV与计算泥沙年变异ΔSVc时间过程比较

表2 黄河中上游流域水沙变异关系模型参数值

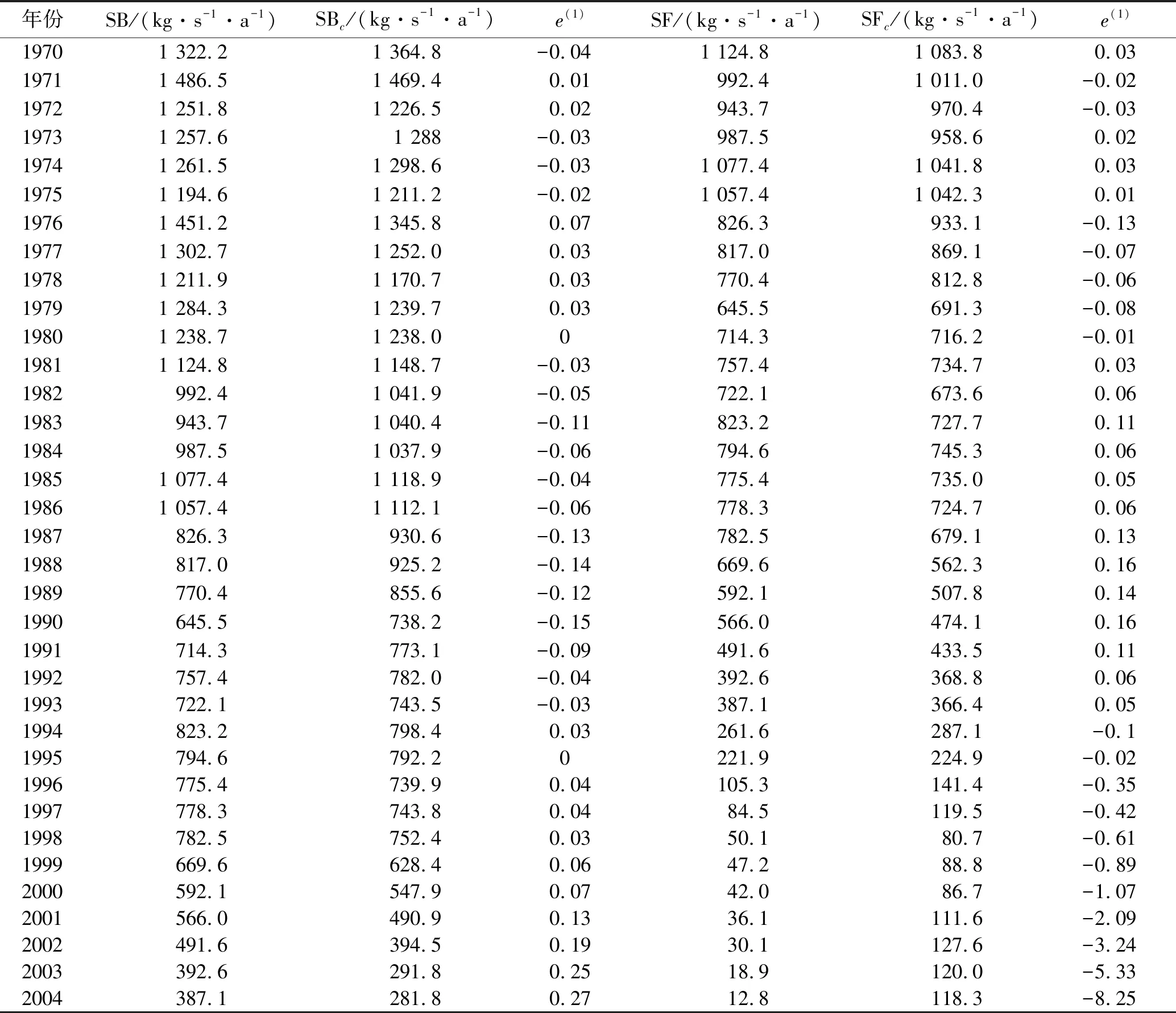
表3 温家川站泥沙变异计算结果

C=0.394e0.009 7(YN-1983)

(22)

式中：YN为年份。据这两个公式可计算得植被覆盖率C的年变化,进而计算出相应的变异值等。

这次模型计算中，由于水利工程的年变化信息和流域面平均蒸发资料难以获得，并为了简化模型检验，先不考虑蒸发和水利工程影响。简化的模型为

(23)

2.3.2 模拟结果与分析 表3中观测的年输沙率向前滑动平均SF与向后滑动平均SB相减得实际输沙年变异ΔSV，类似地计算的年输沙率向前滑动平均SFc与向后滑动平均SBc相减得计算输沙年变异ΔSVc。图1为窟野河温家川站实际泥沙年变异ΔSV与计算泥沙年变异ΔSVc的时间过程比较。从时间系列过程看，泥沙最大变异发生在1998年，其值为-732.4 kg/(s·a)，1979年为其次，泥沙变异值为-638.8 kg/(s·a)。从实际泥沙年变异ΔSV与计算泥沙年变异ΔSVc时间过程变化趋势看，两者十分吻合。图2是实际泥沙年SB与计算泥沙年SBc关系，其两者的关系线接近45°直线，有效性系数DCs为0.974，相关系数RRs为0.987，相对误差只有6.9%。这些结果都说明微分变异模型的结构是合理的，可有效地表达泥沙的变异关系。

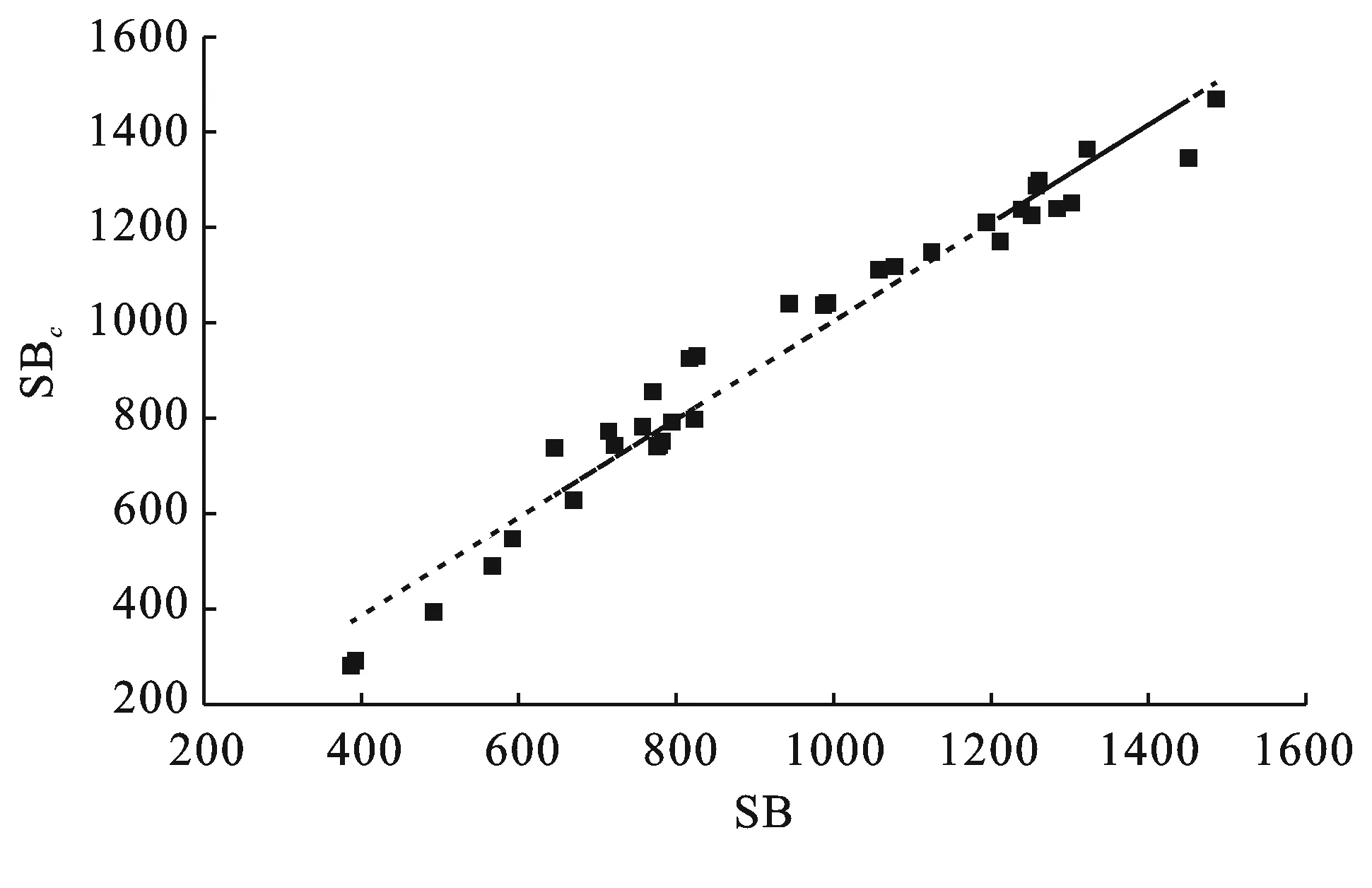
图2 温家川站实际泥沙年SB与计算泥沙年SBc关系线

表4是7个流域水流和泥沙变异模拟的精度统计。泥沙系列变异模拟的有效性系数最大的流域为0.981，最小的也有0.709，说明泥沙变异模拟的有效性在这7个流域是很高的；泥沙变异模拟与实际的系列相关系数大于0.900的有4个，占到了57%，最小的也有0.797，说明泥沙年变异ΔSV与计算泥沙年变异ΔSVc间的相关性在7个流域都是十分显著的；相对误差最小的为4.8%，最大的也只有23.4%，模拟误差不同流域不仅都较小且变化不大，说明变异模型模拟关系很稳定。水流系列变异模拟的精度类似，这里限于篇幅不展开讨论(表4)。

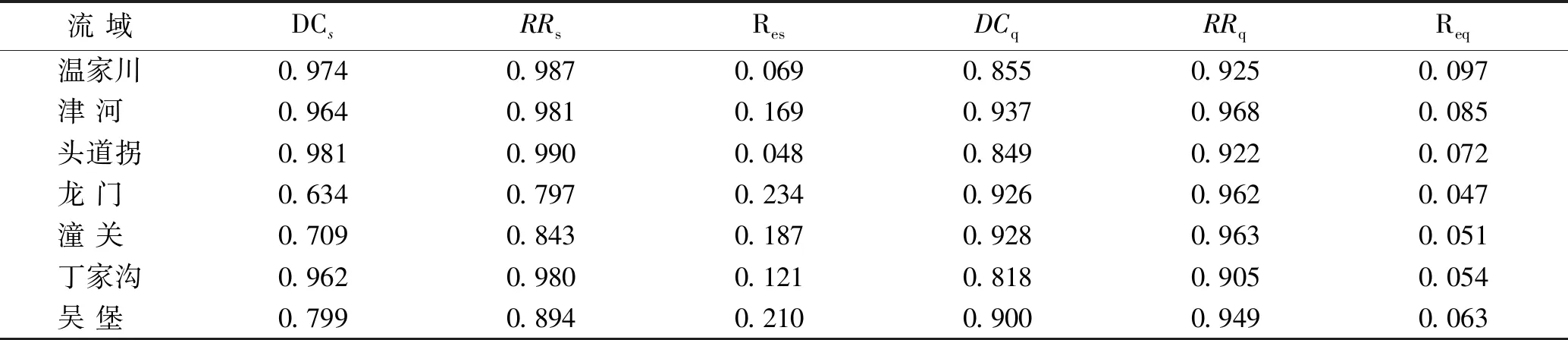
表4 黄河中上游流域泥沙变异模型计算精度

2.3.3 流域平均变异贡献比例分析 为了进一步检验微分变异模型结构的合理性，这里把变异模型用于泥沙变化贡献比例分析。由公式(23)—(24)组成的变异模型，有如下变异贡献比例分析式：

(24)

(25)

式中：前两项之和反映降雨因素改变导致的泥沙变化,后两项之和是由植被覆盖率变化引起的泥沙变异。则气候因素和植被因素变异引起的贡献比例分别为

(26)

式中：CHP，CHC分别表示气候、植被因素变化引起的泥沙变化贡献比例。具体计算结果详见表5。从表5结果看,各个流域不同因素贡献比例略有变化,气候因素变化贡献比例在0.106～0.155,植被变化贡献比例在0.844～0.893,气候、植被平均贡献比例分别为0.129和0.870,这与潼关站的贡献比例十分接近,因为其他6个流域散布在潼关流域内,这全部流域平均与潼关站接近,一方面说明这些流域和相应资料系列的代表性选择合理；第二方面也进一步证明了变异模型结构的合理性和模拟结果的稳定性。

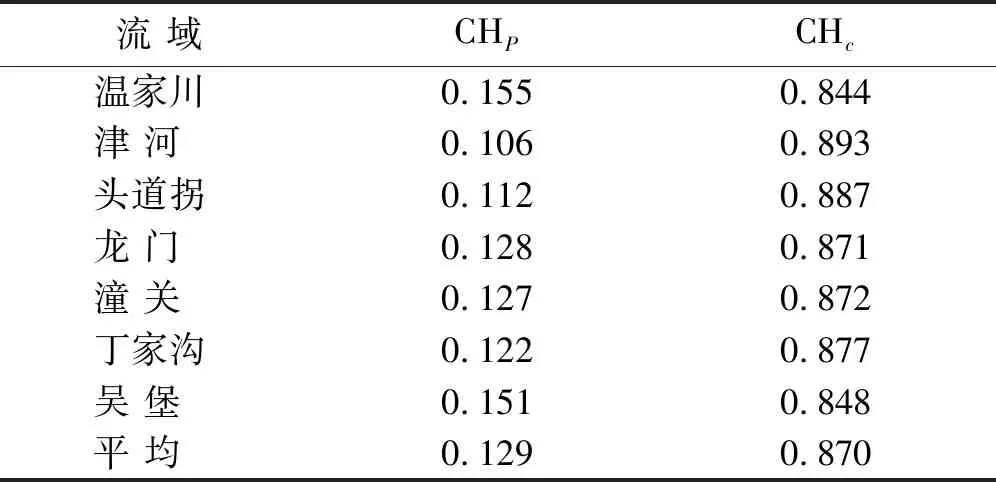
表5 黄河中上游流域平均变异贡献比例

3 结 论

本文以微分为基础，提出直接建立泥沙、水流变异模型，通过黄土高原和黄河中上游7个测站控制流域输沙率和流量变异变量的模拟检验，获得了7个流域输沙率和水流变异模拟平均有效性系数为0.860和0.887，平均相对误差分别为14.8%和6.7%。从水流变异、泥沙变异模拟精度和各因素变异贡献比例3个层面检验了模型，初步证明了结构的合理性和模拟实际泥沙变异具有的高有效性。