基于调速的飞行冲突探测与解脱方法
2021-06-24王红勇邓涛涛徐文强
王红勇,邓涛涛,徐文强
(中国民航大学天津市空管运行规划与安全技术重点实验室,天津 300300)
随着国民经济快速发展,空中交通运输总量进一步提高。2019年,中国民航完成运输总周转量、旅客周转量、货邮运输量、运输起降架次分别同比增长7.2%、9.3%、2.0%、5.1%,达到1293.20亿t·km、 11705.10亿人·km、753.2万t、1165.5万架次。然而在有限的空域条件下,空中交通流量的快速增加,导致航空器间发生飞行冲突的可能性随之增加,与此同时严重影响了飞行安全。飞行冲突探测与解脱方法能够对航空器小于最小安全间隔的趋势进行预警,并提出高效的解脱方法,是空中交通管理系统中的一项关键技术,对保证民航飞行安全发挥着重要作用[1]。
很多学者都对飞行冲突解脱方法进行了研究,并且提出了很多行之有效的方法。2002年,Pallottino 等[2]提出了一种基于混合整数线性程序的冲突探测与解脱方法,这种方法通过改变速度或航向使总飞行时间最少。2004年,Goss等[3]根据航空器当前航迹,使用几何最优接近法进行冲突探测。2006年,Christodoulou等[4]使用混合整数非线性规划使总飞行时间最小解脱飞行冲突,但是此方法需要很长的计算时间。Lecchini等[5]提出了基于蒙特卡罗的随机方法,此方法的不足在于计算时间过长。2006年,夏怡凡等[6]提出调整飞行速度解脱飞行冲突,使航空器飞行时间与预计飞行时间保持一致。但是不足之处在于对于多架航空器的情形,经过一次调速后,有可能出现原来冲突现在不冲突或者原来不冲突现在冲突的情形,所以每次调速后,都必须重新进行冲突的探测。2010年,Cobano等[7]提出基于遗传算法的方法,通过寻找给定航路点最优路径解决飞行冲突。主要缺点在于计算时间具有不可预测性,有限时间内不能保证解的收敛。2010年,何晓菊等[8]对于航线的两架或三架航空器,提出一种动态调整航空器飞行速度的方法来避免发生飞行冲突。该方案是根据经验选定调速区域。并且管制员需要实时监视进入调速区域的航空器的位置变化以及和其他航空器的位置关系。由此带来管制员负荷的增加。2013年,赵嶷飞等[9]基于调速法冲突解脱模型,计算调速区间,重点研究了航线结构对于调配时机的影响。2019年,张思远等[10]提出了航迹规划算法,通过将冲突区域网格化,并且结合遗传算法规划出全局最优的无冲突航迹。但是根据仿真结果可以看出,在短时间内航向变化的次数较多,不适合实际的飞行操作同时增加了管制员的负荷。2019年,王泽坤等[11]优化了速度障碍法模型,该模型可以有效解决飞行冲突,并给出冲突解脱与航迹恢复的位置。2019年,张启钱等[12]提出了低空多机冲突探测与解脱模型,建立了多机冲突探测与解脱规则和流程,仿真验证表明,该方法具有更高的解脱效率且相同计算时间内具有更高的解脱架次极限。2020年,向征等[13]提出混杂模型,通过混杂模型进行无冲突航迹预测,采用调整速度解决航路交叉点的冲突解脱,提出了无冲突航迹规划的方法并进行验证。
上述飞行冲突探测与解脱有一些缺点和不足: 一是算法计算时间太长,或计算时间不可控; 二是在进行飞行解脱时,没有考虑到航空器燃油消耗; 三是通过几何法的飞行冲突探测与解脱实用性较差; 四是需要管制员调配的次数太多,增加了管制员工作负荷。
基于以上不足,现基于航空器速度分配的飞行冲突解脱方法,飞行冲突快速解脱时,充分考虑燃油消耗成本,同时减小管制员工作负荷提高空中交通系统运行安全性。在计算冲突区域内相关航空器调速区间的基础上,通过非线性规划方法找出最佳最省油的调速速度,生成调速剖面图分配给相应航空器。飞行冲突解决后,航空器会恢复到之前的速度,继续沿着计划航迹飞行。
1 问题描述
研究的问题是在飞行冲突有效解脱时,充分考虑燃油消耗成本。通过改变航空器速度剖面解脱冲突,使航空器不偏离计划航迹,从而对管制空域中其他航空器影响最小,同时便于飞行员操作。
首先将空域划分为一系列长方体单元,实现空域离散化,如图 1所示。以航空器进入某个单元时间和离开这个单元时间进行参数化,冲突探测算法将会更简单、更快捷。
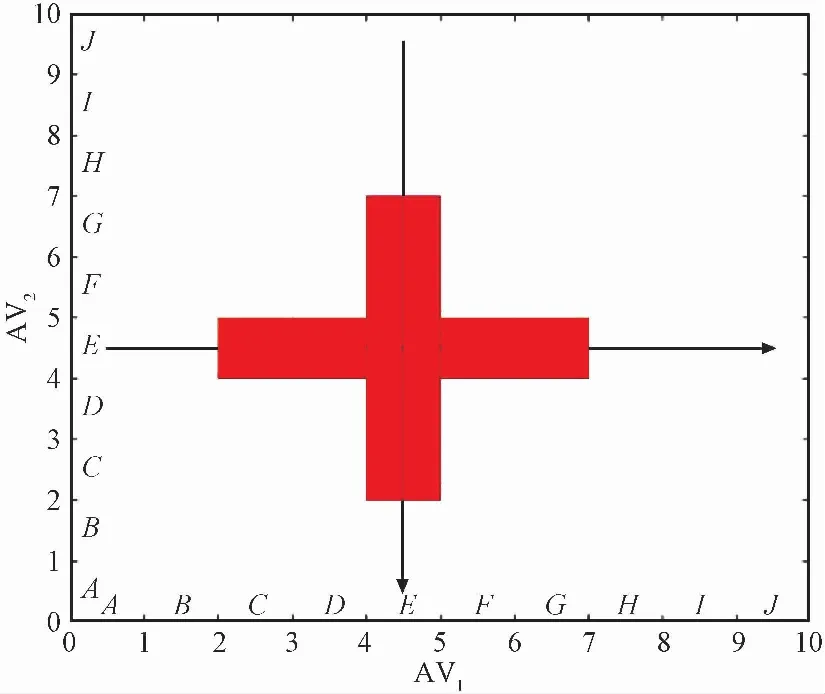
图 1 两架航空器及其冲突区域示意图Fig.1 Schematic diagram of two aircraft and their conflict areas
航空器间安全间隔用一定的单元数进行衡量。为尽量减少空域离散化带来的影响,不增加问题复杂性同时考虑到最小安全间隔,将每个长方体单元的长和宽设为2000m,高设为300m。航空器在每个长方体单元中停留的时间取决于航空器类型及性能。
根据飞行计划确定每个航空器将飞越的单元。设Si为第i架航空器计划航迹。如S1为航空器1 的计划航迹,根据航空器经过的单元,S1=[EJEIEHEGEFEEEDECEBEA]。
将第i架航空器记为AVi。航空器AVi所在单元周围的所有小于最小安全间隔的单元定义为航空器保护区内的单元,记为P(i)。将冲突定义为另一架航空器经过了这架航空器保护区内的单元,即穿过了P(i)。
从图1中可知,AV1和AV2的冲突区域由S1(EG)、S1(EF)、S1(EE)、S1(ED)、S1(EC)和S2(CE)、S2(DE)、S2(EE)、S2(FE)、S2(GE)组成。当两架航空器同时穿过冲突区域时,则两架航空器发生飞行冲突。
2 模型和方法
提出的飞行冲突探测与解脱的方法,适用于解脱多架航空器间的飞行冲突且使得在解脱飞行冲突的机动飞行中航空器能够以最省油的速度飞行。首先,如果探测到两架航空器之间有飞行冲突,将会计算每架航空器的调速区间,用非线性规划的方法优化调速过程中的燃油消耗,找到最优的调速速度,然后分配相应的航空器速度剖面图来解决飞行冲突。
2.1 基本模型
冲突探测与解脱算法目的是获得航空器到达冲突区域的顺序,计算冲突区域内相关航空器调速区间,通过非线性规划的方法找出相关航空器最佳最省油的调速速度,并生成调速剖面图分配给相应的航空器,从而解脱飞行冲突。
考虑图 1的情景,两架航空器仅有一个冲突区域。这个算法给每个航空器建立一个时间序列。将会得到航空器在每个单元中的停留时间。设Ti,j为第i架飞机在第j个单元中的停留时间,计算公式为
Ti,j=ti,j+1[Si(j+1)]-ti,j[Si(j)]
(1)
式(1)中:ti,j+1[Si(j)]为第i架飞机进入第j单元的入口时间;ti,j[Si(j+1)]为第i架飞机进入第j+1单元的入口时间。
采用先到先服务的原则,将航空器预计到达冲突区域的顺序定义为航空器通过冲突区域的顺序。
以图 1中两架航空器和一个冲突区域为例,飞行冲突探测解脱算法流程图如图 2所示。首先得到两架航空器计划航迹,将计划航迹网格化。得到每架航空器在每个单元中的停留时间。然后,检查航空器计划航迹间是否有交叉点。如果没有交叉点,则可以得出航空器间没有飞行冲突。航空器可以按照计划航迹进行飞行。反之,则计算出可能的冲突区域、航空器到可能冲突区域顺序和时间。
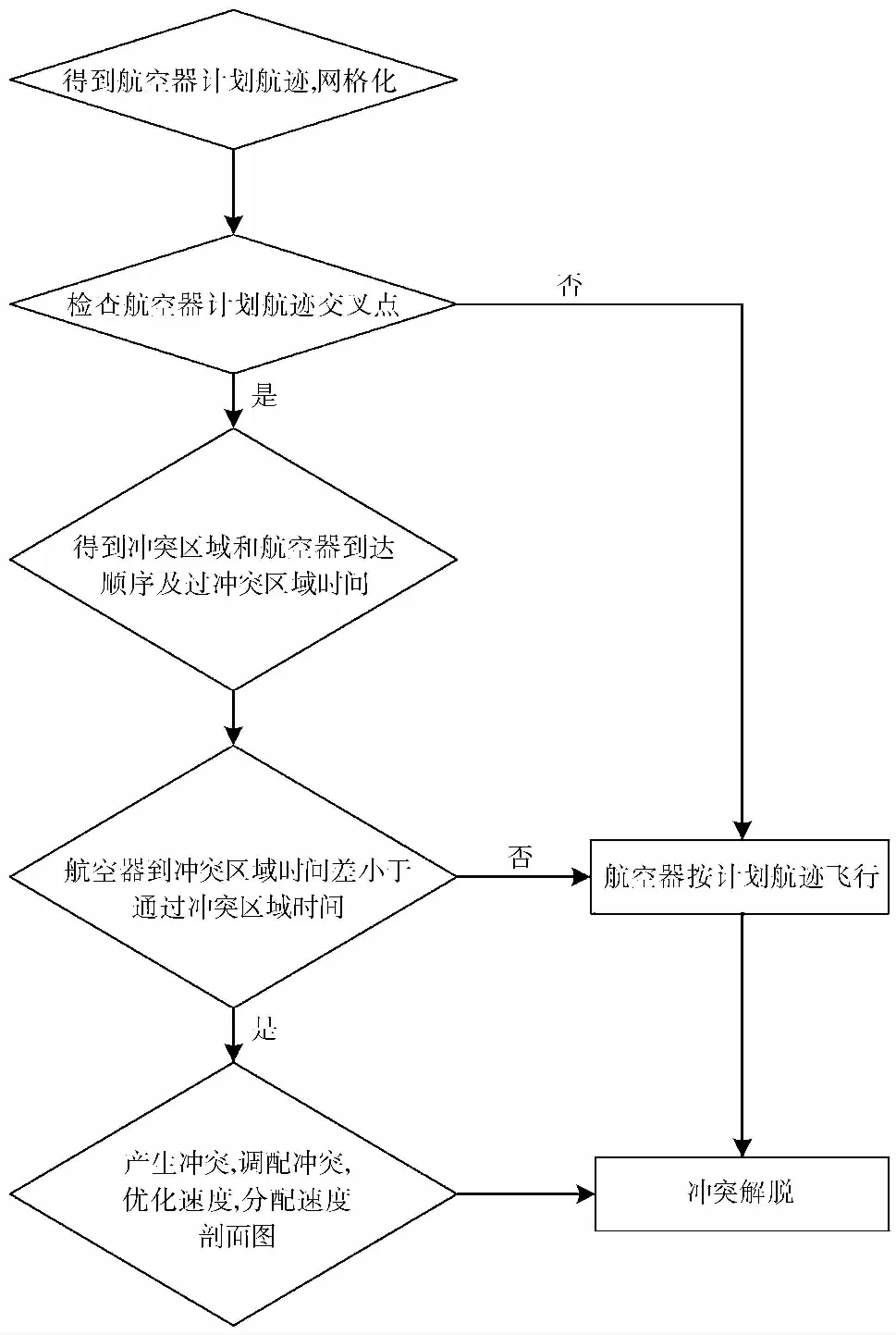
图 2 算法流程图Fig.2 Algorithm flowchart

图 3 两架航空器冲突解脱示意图Fig.3 Schematic diagram of conflict resolution between two aircraft
进一步计算航空器到达可能冲突区域时间差。如果时间差大于前一个航空器通过冲突区域的时间,则不存在飞行冲突。航空器按照计划航迹飞行就不会存在飞行冲突。如果时间差小于前一个航空器通过冲突区域的时间,则产生飞行冲突。通过给该航空器以及相关的航空器分配速度剖面建立一个新的时间序列。
对于发生冲突的航空器,需要调整其速度,通过增减航空器在每个单元中的停留时间来解脱飞行冲突。算法的复杂度随着航空器数量和冲突区域的增多而增加。
为考虑航空器在实际飞行过程中受到的高空风、恶劣天气、飞行员误操作等影响因素。定义了反映航空器到达冲突区域时刻的一个误差函数Ei,计算公式为
Ei=μi+σi
(2)
式(2)中:μi、σi为第i个航空器预计到达冲突区域时间的均值和标准差。由于受到一些因素的影响,航迹的变化、冲突区域的变化可能会影响后期的冲突区域。通过误差函数的值来定义到达顺序。误差函数的值越小,该航空器到达冲突区域的时间越早。
将冲突区域内的最小时间间隔定义为航空器以最大速度通过冲突区域所用的时间。如图 3所示,航空器1先于航空器2 到达预计的航迹交叉点。
航空器1预计在t1时刻到达冲突区域,航空器2 预计在t2时刻到达冲突区域。航空器1和航空器2的时间差小于冲突区域内的最小时间间隔,所以预计航空器1和航空器2之间存在飞行冲突。此时,便可通过调整航空器2的速度来增加其在每个单元中的飞行时间来解脱飞行冲突。如:航空器1在t1时刻进入冲突区域,在t3时刻离开冲突区域。航空器2在t3时刻进入冲突区域,在t4时刻离开冲突区域。
2.2 调速区间的确定
基于调速的冲突解脱方法是当探测到两架航空器或者多架航空器之间存在飞行冲突时,航空器通过加速或者减速的方法来进行冲突解脱。航空器之间的冲突解脱后,航空器要恢复计划的飞行速度。
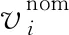

图 4 梯形速度变化图Fig.4 Trapezoidal speed change graph
(3)
在飞行距离为D时,航空器进行调速机动飞行与正常匀速飞行产生的时间变化设为ti,即
(4)
进一步在式(3)中加入航空器加速度和速度的界限,可得到航空器进行调速机动飞行与正常匀速飞行在总飞行距离为D时产生的时间变化的极值为
(5)
(6)
由此得到在一定距离上航空器进行调速机动飞行与正常匀速飞行产生的时间差。然后根据航空器到达冲突区域的顺序和时间差,可以得到冲突解脱的方案,接着可得出有关航空器的调速区间。
2.3 速度优化
根据冲突解脱方案中的航空器调速区间,要进一步对调速阶段的燃油消耗进行优化,在调速区间中找到一个最省油的速度值。
假设条件如下。
(1)飞机在预定时间范围的开始和结束时以平均速度飞行,涉及速度导数的项在时间区间内积分为零。
(2)航空器的飞行高度一定。
(3)忽略15min之内航空器由于燃油消耗而带来的质量变化。
飞机基础数据(base of aircraft data,BADA)包含294种不同飞机类型的性能和运行过程参数。根据BADA中的参考模型,得到单位时间的燃油消耗[14]为
(7)
式(7)中:m为航空器的质量;c1为第一推力比油耗系数;c2为第一推力比油耗系数;α为第一燃料流量系数;β为第二燃料流量系数;c1、c2、α、β取决于航空器的类型。综合假设条件,可知Ct是一个只随速度改变而改变的量。进而得到单位距离的燃油消耗公式为
(8)
(9)
为了评估航空器AVi的燃油消耗,取航空器机动过程中的速度平均值vmean,可由式(11)得到,即
(10)
(11)

(12)

对于每架飞机,在其可调速的区间内要找到一个最合适最省油的速度值。这是一个多目标非线性规划问题。把冲突区域内涉及的所有航空器在冲突解脱这段距离中的燃油消耗求和,然后求出最小值。这就把一个多目标问题转化成一个单目标的问题。通过解决一个单目标问题找到每架航空器的最佳调速速度。
目标函数为
(13)
约束条件为
(14)
由于上述目标函数是非线性函数,约束条件中既有线性约束条件也有非线性约束条件。根据目标函数、约束条件以及决策变量可以得出这是一个有约束的多维非线性规划问题。可以利用MATLAB中的fmincon函数,选用其中的内点算法来求解。最终计算出每架航空器的最佳调速速度。
3 算例分析
以下对本文算法进行仿真验证。首先来研究算法计算时间的影响因素。仿真情景如图 5所示。
由图5可知,仿真环境为区域管制空域。将空域划分为长、宽为2000m,高为300m的单元。由于空域单元的高度为300m,不同高度层的航空器之间不存在飞行冲突。所以只考虑同一高度层的情况。将航空器间的最小安全间隔设为5个单元。在模拟情景基础上,来研究冲突探测与解脱算法计算时间的影响因素(图6)。算法的计算时间可能与一个管制扇区内的航空器数量,所选取的航空器的计划航迹的长度和最小安全间隔有关系。
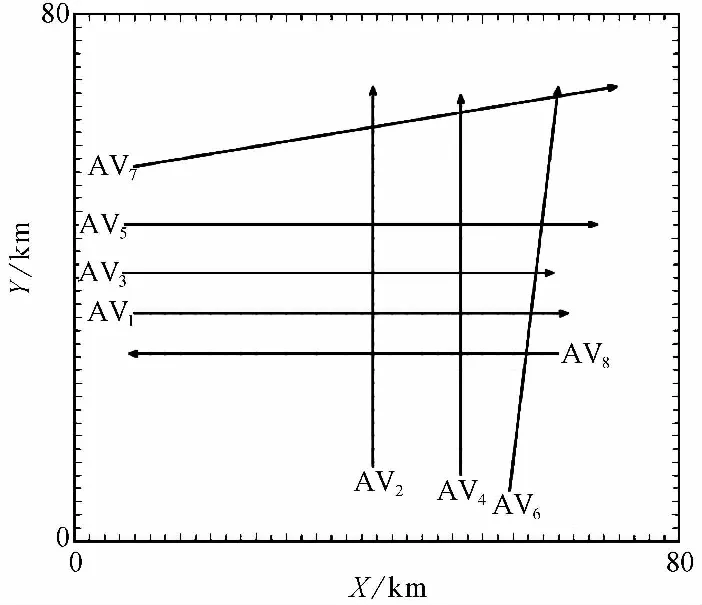
图 5 模拟情景图Fig.5 Simulation scenario map

图 6 算法计算时间和航空器数量之间的关系Fig.6 The relationship between the calculation time of the algorithm and the number of aircraft
从图 6中可以看出,当航空器数量在8架以内时,算法可以在几秒钟内求出解。根据图6的黑线可以看出,随着航空器数量的增加,飞行冲突探测所需的计算时间逐渐增加,这是因为冲突区域的增多而带来计算量增大。而且黑线表示的算法计算时间的变化率不大,最终当航空器数量为10时,冲突检测的时间也在3s内,这说明冲突探测算法的效率较高。根据图6的红线可以看出,随着航空器数量的增加,冲突解脱和优化调速速度所需时间在增加。这是因为随着冲突区域的增加,约束条件也在增加。红线表示的算法计算时间变化率较大,当航空器数量在9架以内时,所需计算时间在10s以内。Jose等[15]提出搜索树算法在航空器数量为10时,计算时间达到了325s。这说明提出的冲突探测与解脱算法比较有效率。
航空器数量为8架时,算法计算时间与最小安全间隔单元数量间的关系如图 7所示。随着最小安全间隔对应单元数量的增加,算法计算时间不断增加。由于冲突区域不断增加,使算法计算时间增加。
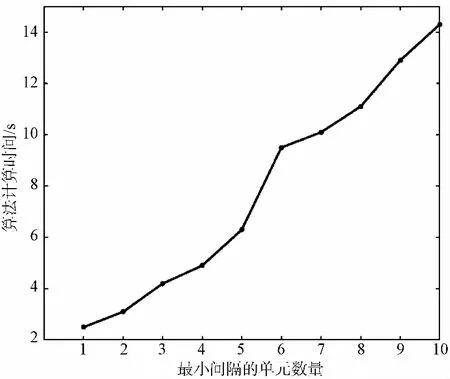
图 7 算法计算时间和最小间隔单元数量之间的关系Fig.7 The relationship between algorithm calculation time and the number of minimum interval units
以5km计划航迹长度为单位1来进行仿真计算,探讨算法计算时间和管制空域内的计划航迹的长度之间的关系。如图 8所示,随着计划航迹增加,算法计算时间随之增加。

图 8 算法计算时间和计划航迹长度之间的关系Fig.8 The relationship between algorithm calculation time and planned track length
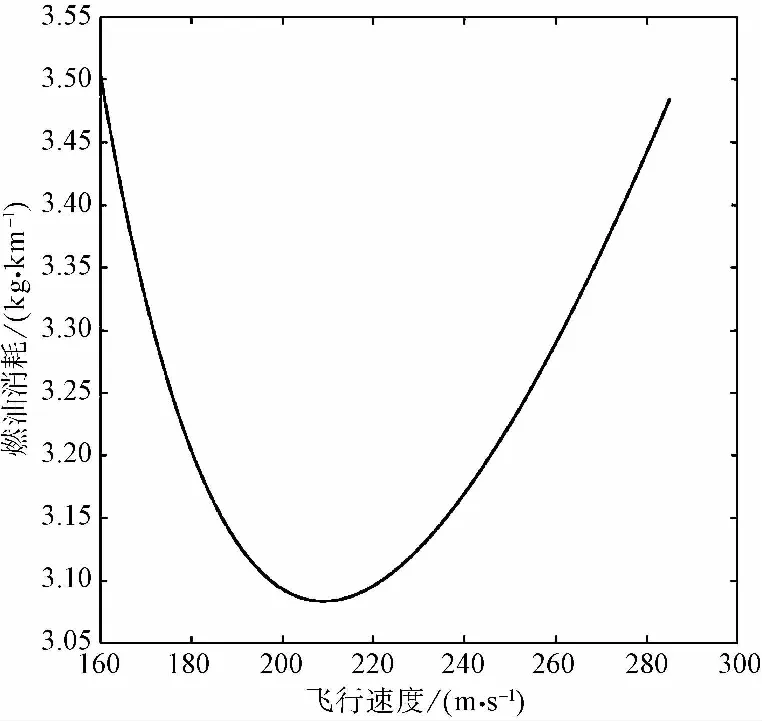
图 9 飞行速度和燃油消耗关系图Fig.9 Relationship between flight speed and fuel consumption

图9 所示为10100m飞行高度上的速度和燃油消耗的曲线图可以看出,随着飞行速度的增加,燃油消耗量先减小后增加。燃油消耗量在飞行速度为210m/s是取得最小值为3.075kg/km。
AV1与AV2的交通态势如图 5仿真情景中的AV2和AV6。在检测到飞行冲突,然后通过飞行冲突与解脱算法为每架飞机计算出调速区间来避免飞行冲突。以调速区间的速度为变量,计算飞机进行机动的这段距离的燃油消耗。通过非线性规划的算法算出了两架飞机在机动过程中调速速度和燃油消耗的关系如图 10所示。
从图 10中可以看出,当第一架飞机的调速速度为218.8m/s,第二架飞机的调速速度为183.8m/s时,机动过程中的燃油消耗量最小为233.58kg。而且从图10中可以看出在满足冲突调配的前提下,机动过程中燃油的消耗量的最大值为248.44kg。利用本文算法进行冲突调配,在整个调速机动过程中可以有14.86kg的燃油节省。
根据上文确定的最佳调速速度,然后为每架飞机分配调速剖面图。调速剖面图如图 11所示。
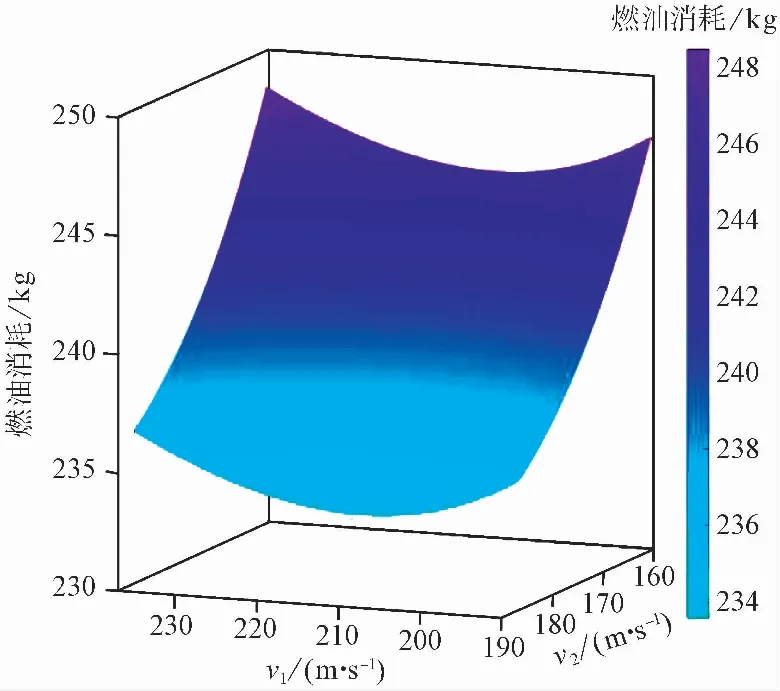
图 10 机动过程调速速度和燃油消耗关系图Fig.10 The relationship between speed regulation speed and fuel consumption during maneuvering

图 11 调速剖面图Fig.11 Speed control profile
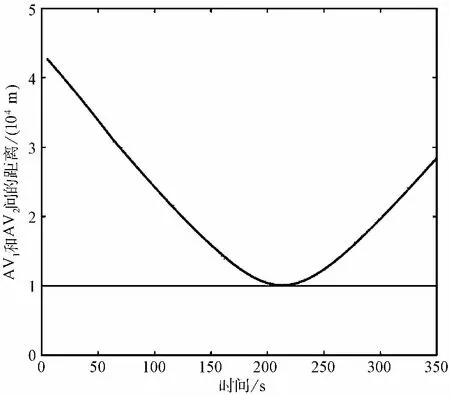
图 12 AV1和AV2间距离关系图Fig.12 Distance diagram of AV1 and AV2
根据两架飞机的速度剖面图可以得出两架飞机之间的距离关系图如图 12所示,两架飞机之间的最小距离为10km,满足最小安全间隔的要求。由此验证提出的冲突解脱算法和非线性规划确定最省燃油的调节速度方法的有效性。
4 结论
提出了一种有效的飞行冲突检测与解脱的方法。在繁忙的管制空域中,通过改变每架航空器的速度剖面来解决飞行冲突。本文算法的冲突探测与解决算法的效率较高,计算时间较短。探究了算法计算时间的影响因素。通过飞行冲突检测与解脱算法得出了航空器可以进行调速的速度区间,然后通过非线性规划的方法优化调速机动阶段的燃油消耗。得出最省油的调速速度,然后得出相关航空器的调速剖面图。由仿真分析可知,提出的飞行冲突检测与解脱算法耗时较短比较有效,非线性规划优化调速阶段燃油消耗的方法能够带来较大的燃油节省。未来的飞行冲突检测与解脱可以考虑结合改变速度和航向同时考虑燃油经济性。
