黏塑性蠕变模型中屈服强度的确定方法

2021-06-24何志磊任朋勋

科学技术与工程 2021年13期

何志磊，任朋勋

(1. 华北水利水电大学岩土工程与水工结构研究院，郑州 450046； 2. 国家林业和草原局昆明勘察设计院，昆明 650216)

在岩石流变模型研究中，模型理论因概念直观、简单，同时也能全面反映流变介质的各种流变特性，获得了广泛应用。模型理论是用3个理想元件：弹簧、黏壶和滑块(也称圣维南体)分别表示理想的弹性、理想的黏性和理想的刚塑性，通过这3个基本元件的串、并联组合来描述岩石复杂的流变变形特征。夏才初等[1-2]根据岩石基本流变力学特性，提出了岩石的统一流变模型，所有的流变力学模型经过结构元件变换，都可以变换为统一流变模型，并给出模型的辨识方法，这为理论流变力学模型的正确使用提供了指南。但由于组成元件模型的元件都是线性元件，无论串联或并联多少个元件，其串、并联之后的模型仍然是线性模型，可以描述衰减蠕变阶段和稳定蠕变阶段，但不能有效反映加速蠕变阶段的特征。为了能够全面描述复杂的蠕变特性，非线性元件逐渐被提出来，通过对线性元件模型进行修正，得到非线性的蠕变模型，使得模型能够准确全面描述岩石非线性蠕变特性，甚至可以描述加速蠕变阶段的特征[3-6]。早期的修正方法多数是在线性元件基础串联一个非线性元件，但随着研究的深入，基于非定常参数的蠕变模型和采用损伤力学或分数阶理论等多学科交叉建立的修正模型越来越常见[7]，这些修正的模型多是对模型中黏性元件或弹性元件的修正，对塑性元件关注的不多。元件组合模型中，塑性元件用滑块表示，当应力大于屈服强度时，就发生塑性变形，小于就不发生，实际上就相当于是一个分段函数的功能，把蠕变变形分为黏弹性变形和黏塑性变形。但在蠕变模型研究中对是否发生塑性的判断条件——屈服强度的确定并没有详细的方法，部分学者认为屈服强度就是长期强度。例如徐卫亚等[5]在建立绿片岩的非线性黏弹塑性流变模型中认为σs表示屈服应力或是长期强度，对这两者并没有明确的区分。蒋昱州等[8]在建立统计损伤流变模型过程中直接用长期强度代替了屈服强度。齐亚静等[6]指出黏塑性变形的三维蠕变本构关系应该用岩石的屈服函数和塑性势函数表示，而不是用一维的长期强度σs表示，也是认为在一维情况下σs表示长期强度。吴斐等[9]在建立分数阶黏弹塑性蠕变模型中，利用等时曲线法得到长期强度后，认为σs与长期强度等价。周小棚等[10]对提出改进西原模型进行验证时，同样是认为长期强度为屈服强度σs。苏腾等[11]在进行分数阶模型验证的时候，先求解出三轴下的煤岩的长期强度，认为σs等于长期强度，然后进行反演分析。

从组成元件模型的塑性元件看，屈服极限或者屈服强度是表示岩石是否发生塑性的条件，而长期强度表示的是岩石长期不发生破坏的最小力，两者的物理意义是不同的，在数值上，屈服强度能否等价于长期强度，需要明确这两个概念及其之间的关系。因此，现从概念和物理意义等方面阐述这两个物理量的含义及它们之间的关系，并采用作图法给出蠕变中屈服强度的确定方法。

1 蠕变中屈服强度与长期强度的关系

根据材料力学，屈服强度是材料发生屈服现象时的屈服极限，大于屈服强度后材料将发生不可恢复的塑性变形。而在元件模型中，采用塑性元件模拟物体的塑性，如图 1所示，它是由两接触面粗糙的滑块组成，所以有时也称为滑块或摩阻件，σ为作用在岩石上的长期荷载，它具有一个起始的摩擦阻力σs，若外力小于此起始摩擦阻力，则不产生变形，若大于此值时，它在等应力下出现塑性流动，这个摩阻力称为屈服应力(屈服强度)，一旦应力除去，变形也不会恢复，留下永久变形。

图 1 塑性元件受力示意图Fig.1 Plastic element stress diagram

由于出发点不同，长期强度的概念有不同的表述。刘雄等[12]给出的长期强度的定义为：岩石在长期的应力场或变形场的作用下能保持岩体稳定的最大应力，即在这一应力值时，材料将发生破坏而未发生破坏，也可以定义为：在指定的岩石工程运行的时间内，岩体不发生破坏的最大可能的作用力。孙钧[13]给出的长期强度的定义是岩体强度随时间而持续有限降低，并逐渐趋近于一个稳定收敛的低限定值。

从概念上看，屈服强度和长期强度的物理含义是完全不同的，但实际上，在蠕变过程中两者之间是相关的，这主要得益于采用等时曲线法确定岩石长期强度的过程和原理。等时曲线法是目前应用比较广泛的确定岩石长期强度的方法，并引入相关的岩石力学试验规范。采用等时曲线法确定岩石的长期强度，通常是根据波兹曼叠加原理，在一簇不同应力水平的蠕变曲线上，做一条与纵轴平行的直线，使得该直线与不同应力下的蠕变曲线相交，且利用各交点的应力-应变值绘制曲线，由此而获得在应力-应变坐标下的等时应力-应变曲线，也称为等时曲线。根据等时曲线的形态特征确定其屈服极限值，并将各等时曲线的屈服极限值的连线所组成的水平渐近线在应力轴上的截距作为长期强度值，如图 2 所示，由此可知，长期强度是由屈服点的渐近线确定的，说明了屈服强度和长期强度的关系，且长期强度是要小于屈服强度的，可以认为长期强度是在时间趋于无穷时的屈服极限，并且通过把不同时刻的屈服强度与相应的时间表示出来，如图 3所示，可以知道屈服强度随着时间是减小的。

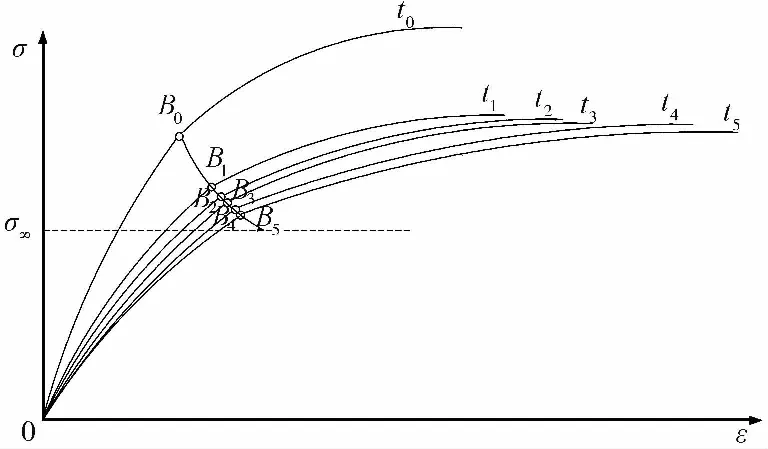
B0、B1、B2、B3、B4、B5为屈服线上的点图 2 等时应力-应变曲线Fig.2 The isochronous curve

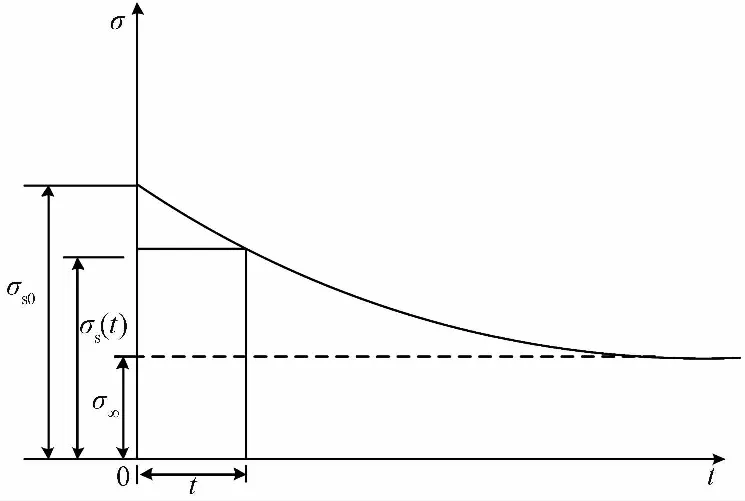
图 3 屈服强度随时间的变化规律Fig.3 The law of yield strength with creep time

屈服强度随时间的变化规律[14]可以表示为

(1)

式(1)中：σs为岩石的屈服强度；σ为作用在岩石上的长期荷载；σ∞为岩石长期强度，数值上等于岩石的长期屈服极限σs∞；σs0为岩石瞬时屈服强度，可以通过常规力学试验得到；α为反映岩石损伤的参数，其大小与岩石的材料特性和外荷载有关，可由试验确定；t为岩石开始发生屈服后的持续时间，数值上等于岩石开始加载的持续时间减去作用力小于屈服强度作用的时间。

根据式(1)，当岩石受到的应力小于等于长期强度时，屈服强度为瞬时的屈服强度，当受到的应力大于长期强度时，屈服强度随加载时间增长而减小，变化的区间为从长期强度到瞬时屈服强度。在蠕变模型中塑性元件被看作是滑块，从物体摩擦特性进行比较分析，屈服强度就相当于是摩擦力，瞬时屈服强度相当于静摩擦力，而长期强度相当于动摩擦力，静摩擦力在数值上是大于动摩擦力，也就是瞬时屈服强度大于长期强度。

2 蠕变中屈服强度的确定方法

由于屈服强度是随时间变化的，直接确定屈服时间是困难的。Goodman[15]研究岩石蠕变应变轨迹与岩石全应力-应变曲线之间的关系，分析了岩石蠕变破坏点与全应力-应变曲线下降段(破坏段)具有很好的相关性。许宏发等[16]在此基础上，把全应力-应变曲线和等时曲线联系起来，研究了软岩的蠕变寿命估计。同样借助于蠕变应变轨迹与岩石全应力-应变曲线的关系，通过作图确定岩石蠕变中的屈服强度及屈服发生的时刻。

按照等时曲线法求解长期强度的步骤，把等时曲线的屈服点相连，同时在同一坐标系中绘制全应力-应变曲线，得到结果如图 4所示。

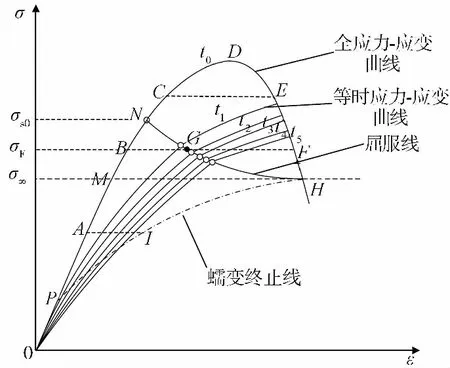
图 4 全应力-应变曲线与等时应力-应变曲线的关系Fig.4 Relationship of complete stress-strain curve and isochronous curve

在图 4中，蠕变过程为一条水平直线，累积应变与全应力-应变曲线的下降段相交时蠕变发生破坏[16]。PH表示蠕变终止线，NH表示屈服线，屈服线标志着岩石由黏弹性阶段向黏塑性阶段转化，岩体内部结构发生劣化。由此可以把岩石发生蠕变的过程分为不同的区域：蠕变终止线PH以下区域，表示不发生蠕变变形；PMH区域表示发生蠕变变形，但最终变形趋于稳定；MNH区域表示发生黏弹性变形而不发生黏塑性变形；NH以上区域表示不仅有黏弹性变形还有黏塑性变形。

根据不同区域的特征，屈服强度的确定方法分为3种情况进行讨论。

(1)如果作用力σF≤σ∞，岩石未损伤或是仅有局部损伤，岩石的整体强度未发生改变，对应于PMH区域，蠕变到达终止线后变形不再变化，趋于稳定，例如蠕变试验起始于A点，经过一定时间后(无穷大)，接近I点而趋于稳定。此时屈服强度可以取为瞬时屈服强度σs0，瞬时屈服强度大于长期强度，也就大于作用力σF，所以此时蠕变模型中的滑块未滑动，不发生塑性变形，只发生黏弹性变形。

(2)如果作用力σ∞<σF<σs0，蠕变达到全应力-应变曲线下降段后将发生破坏，例如蠕变试验起始于B点，经过一定时间至F点而发生蠕变破坏。然而，在加载的初始时间内岩石是不发生黏塑性的，只有黏弹性变形，随着作用时间增长，屈服强度σs(t)逐渐减小，在G点发生屈服，之后才发生黏塑性变形。根据G点的位置与等时曲线的关系，可以获得开始发生塑性屈服的时刻，岩石开始加载的持续时间减去此时刻的时间即为岩石开始发生屈服后的持续时间。之后，在黏塑性计算中，屈服强度随时间逐渐减小，利用式(1)计算得到此时的屈服强度及随着时间逐渐减小的规律。

(3)如果作用力σF>σs0，蠕变达到全应力-应变曲线下降段后同样将发生破坏，岩石开始加载后不仅有弹性变形，同时发生塑性屈服，产生塑性变形，例如蠕变试验起始于C点，经过一定时间至E点，达到加速蠕变而破坏，此时屈服强度的取值也是由蠕变时间来确定的，所不同的是岩石开始发生屈服后的持续时间即为岩石加载的持续时间。

采用如上所述的方法确定岩石蠕变中的屈服强度在理论上是合理和完善的。但这个分析过程只是对采用等时曲线法确定岩石长期强度的情况有效。下面采用上述的方法，以最简单的弹黏塑性模型(广义宾汉姆模型)为例进行具体分析。

经典的广义宾汉姆模型如图 5所示，其蠕变本构方程为

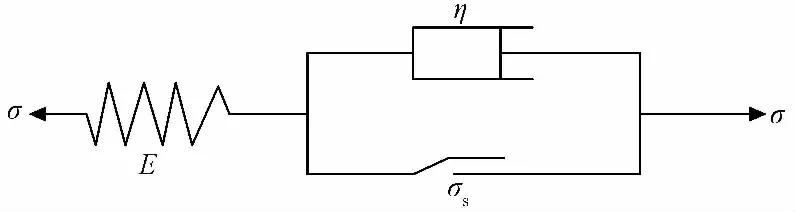
图 5 广义宾汉姆模型Fig.5 General bimgham model

(2)

式(2)中：E为弹性模量；η为黏性系数。

这里的屈服强度认为是一个定值，把作用力分为小于屈服强度和大于屈服强度两部分，但根据本文前面的叙述，屈服强度是随时间变化的，作用力可以分为3种情况进行分析，因此可以对广义宾汉姆模型重新讨论。

(1)当作用力小于长期强度时，此时屈服强度为瞬时屈服强度，作用力小于屈服强度，不发生塑性变形，只有弹簧表示的弹性变形。

(2)当作用力大于长期强度且小于瞬时屈服强度时，根据前面分析，岩石蠕变过程中需要加载一定时间后才发生屈服，发生黏塑性变形。此时，屈服强度等于作用力，小于瞬时屈服强度。假定开始发生屈服的时间为ts，那么屈服后的时间为作用力加载时间减去发生屈服的时间，即为t-ts，根据式(1)，屈服强度是随着时间逐渐减小，可以表示为σs=σ∞+(σs0-σ∞)e-α(t-ts)。

(3)当作用力大于瞬时屈服强度时，岩石起始就屈服，根据式(1)，屈服强度是随着时间逐渐减小，σs=σ∞+(σs0-σ∞)e-αt，这里的t为作用力加载时间。

根据以上3种情况，给出相应的蠕变方程为

(3)

式(3)中：ts为开始发生屈服对应的时间，可以令式(1)的屈服强度等于作用力求得。式(3)即为考虑屈服强度随时间变化得到的广义宾汉姆模型的蠕变本构方程。

如果不考虑屈服强度随时间的变化，瞬时屈服强度等于长期强度，式(3)就可以退化为经典的广义宾汉姆模型。当然，对于包含塑性元件的蠕变模型都可以进行类似的分析。

通过比较是否考虑屈服强度随时间的变化，发现2种情况下的屈服应力差值为(σs0-σ∞)e-αt，也就是如果采用长期强度代替屈服强度计算得到过应力是偏大的，在蠕变变形中就会多计算发生的黏塑性变形，蠕变变形差值为

(4)

结合图 4分析，实际上就是把MNH区域的全部或部分黏弹性变形计算为黏塑性变形，使得蠕变计算中的黏塑性变形计算量偏多。但根据Goodman原理，蠕变迹线与全应力-应变曲线下降段的交点是不变的，发生蠕变破坏时的总的蠕变变形是相同的。也即是说屈服强度随时间的变化的分析，只影响蠕变计算中的黏塑性和黏弹性变形量在总的蠕变变形中的份额，而总的蠕变变形量是不变的。

实际上，瞬时屈服强度和长期强度在数量上可能差距不大。沈明荣等[17]采用等时曲线法对红砂岩的长期强度特性进行试验研究，每条等时曲线的拐点对应的荷载基本都在24MPa左右，没有表现出明显的屈服强度下降的现象，表明这两个值差别是比较小的。对部分学者开展的蠕变试验中的屈服强度和屈服时间的关系，按照式(1)计算整理得到不同岩石的反演参数、瞬时屈服强度和长期强度，如表 1所示。

表 1 不同岩石的瞬间屈服强度和长期强度Table1 instantaneous yield strength and long-term strength of different types of rock

从表 1 可以看出，大理岩和坝基软弱夹层的瞬时屈服强度和长期屈服强度在数值上差别并不大，但泥质板岩的差距较大，可能与岩性、试验设备和试验条件有关。对于差值比较小的情况，可以按照屈服强度等于长期强度进行使用，而对于差值比较大的情况，建议按照本文方法，分情况确定准确的屈服强度。从工程安全角度讲，由于长期强度小于屈服强度，直接用长期强度来代替屈服强度，计算的结果偏于安全，这种做法是可以接受的，但在精确性方面就有所不足，而提出的确定方法考虑了屈服强度随时间减小的现象，能够更为准确地确定屈服强度，在计算黏塑性变形时能够在一定程度上提高计算结果的准确性。

对于一定服务期限的岩石工程，可以有效利用岩石的时效强度进行设计。当岩石工程服务期限相当长(时间趋于无穷)时，应该采用长期强度进行设计，而对于工程服务期限仅为一段时间的临时工程，则可以采用服务期限的最小屈服强度作为设计值。

当作用力大于瞬时屈服强度，根据服务期限的时间，可以根据式(4)的第三种情况，求得服务期的最小屈服强度，以此作为设计强度；当作用力小于瞬时屈服强度，而大于长期强度时，首先根据作用力等于屈服强度，求得开始屈服的时间ts，如果服务时间小于ts，则此时的屈服强度可以作为设计值，如果服务时间大于ts，则按照式(4)中的第二种情况，计算服务时间内的最小屈服强度，并作为设计值；如果作用力小于长期强度，则在服务时间内不会发生破坏。