工程安全双重监管博弈演化的波动效应与机制优化研究＊

2021-06-24张羽杜倩刘红勇袁庆真

科技促进发展 2021年7期

■ 张羽杜倩刘红勇袁庆真

1.西南石油大学土木工程与测绘学院成都 610100

2.永威置业集团有限公司郑州 450000

0 引言

2015～2019年，我国固定资产投资对GDP 增长贡献率稳居高位。与此同时，建筑业安全生产事故频繁发生，典型事故包括：2015年深圳渣土堆放场发生特大滑坡，造成73人死亡，直接经济损失8.81亿元；2016年江西丰城电厂施工平台倒塌，导致73 人死亡，直接经济损失10197.2万元；2020年福建泉州防疫酒店坍塌，导致29人死亡，同时造成了极恶劣的社会影响。由此可见，建筑业的安全生产形势依然严峻，提高工程安全治理水平刻不容缓。

工程安全治理受到技术[1-2]、管理[3-4]、文化[5]等众多因素的影响。其中，安全监管作为确保工程企业合规操作的重要制度安排，起到至关重要的作用。当前关于工程安全监管或风险治理的研究大致可分为“单一监管”和“多方协同监管”两大类。单一监管方面，Zwetsloot等[6]和Hopkins[7]均认为，政府与市场在安全监管方面缺乏有效配合是导致工程安全事故频发的关键。邱聿旻等[8]运用“激励-监管”治理模型论证了政府在防治工程风险中能够发挥的多种监管功能。赵泽斌和满庆鹏[9]通过演化博弈分析找出了公共部门和私人部门风险管理行为存在5 个均衡点，并认为风险感知因素会导致均衡条件难以达到。多方监管方面，Liu 等[10]认为动态惩罚控制场景可以使利益相关者之间的互动更加稳定，优化后的动态惩罚激励方案可以促使企业安全生产。陈宋生等[11]通过XBRL技术研究双重监管模式下公司治理效果发现，监管部门之间协同配合是提高治理效果的前提。Guo等[12]通过调查不同项目治理结构对风险管理的影响后认为，项目利益相关者都应当围绕统一目标调整自身项目治理结构。Renn[13]通过探讨利益相关者的知识、价值和利益整合问题，强调了利益相关者的有效参与是风险治理成功的关键。Zeng 和Chen[14]通过安全监管演化博弈分析提出了建立新的利益和风险分担机制，引入适当的外部监督约束机制的建议。许树生等[15]通过对发包人-承包人-保险人3 方演化博弈分析，提出要强化风险共管、加强3 方协同治理结果的稳定性。许树生等[16]通过社会网络分析构建城市地下工程核心安全风险治理的社会网络模型，提出了相关主体组成的最优结构。丁翔等[17]通过对联合体牵头方与联合体成员之间的博弈分析发现联合体牵头方只有在有效识别各成员公平偏好特征后才能制定合理的风险分配策略。以上研究从监管功能、组织结构、交互作用等方面探讨了工程风险治理和监管问题，具有一定的理论意义和现实价值。然而，鲜有文献从社会综合效益的角度考察最优监管层级和数量问题，也未见有讨论多重监管系统演化波动规律和边界条件的文献。

综上所述，本文将社会综合效益引入模型中，构建了包含施工、监理和安监三方的复制动态演化博弈模型，并运用数值仿真技术进行演化分析，以探索不同监管模式和变量取值条件下博弈主体策略选择和综合效益演化规律，为完善当前工程安全监管机制提供借鉴。

1 模型构建

1.1 模型假设

假设1 博弈中只存在施工单位、监理单位和安检单位3类群体，3类博弈群体可选择的策略分别为合规或违规操作、严格或放松监理、检查或不检查。

假设2施工单位合规操作时事故风险损失为0；施工单位违规操作时有一定几率被严格监理和检查的监理、安监单位发现并纠正，但若监理、安监单位不实施监管，则事故风险损失达到最大值L，L∈(0, )

+∞。

假设3 事故风险损失由施工、监理、安监3 方与外部社会共同承担，分担比例为k,k∈[0, 1 ]。k越大表明项目3方承担事故损失越多，取1时表示事故损失全部由项目三方承担，取0 时表示损失完全由外部社会承担。由项目3 方承担的损失，施工、监理、安监对应的分担比例为h1,h2,h3，且满足h1+h2+h3= 1。

假设4 监理、安监单位严格监理和检查后发现施工单位违规并处罚整改的概率分别为r1、r2，安监单位实施检查发现监理单位放松监理并处罚整改的概率为r3。

根据假设4进一步推理可知，当安监单位实施检查、监理单位严格监理时，施工单位违规未被任何一方发现的概率为l1=(1-r1)(1-r2)，即为该情况下的风险损失系数；当安监单位实施检查、监理单位放松监理时，施工单位违规有r2概率被安监单位直接发现，也可能是安监单位先以r3概率发现监理单位放松监理并纠正，然后监理单位以r1的概率发现施工单位违规操作并纠正，因此该情况下的风险损失系数l2=(1-r1r3)(1-r2)；当安监单位不实施检查、监理单位严格监理时，风险损失系数l3= 1-r1。

1.2 收益矩阵

根据以上假设，构建工程项目施工过程中施工、监理和安监3方的收益矩阵如下表1和表2所示：

表1 安监单位检查时3方收益矩阵

表2 安监单位不检查时3方收益矩阵

安监单位实施检查的3 方收益矩阵如表1 所示。在施工单位合规操作情况下，施工单位仅需支付成本I，而监理单位则需在严格监理时支付监理成本C1，在放松监理时支付安监单位的处罚r3P3及整改成本r3C1；而安监单位除了需支付检查成本C2外，还会在放松监理时获得处罚收益r3P3。在施工单位违规操作情况下，若监理单位严格监理，则其获得处罚收益r1P1并支付严格监理成本C1及风险损失h2l1kL，安监单位获得处罚收益r2P2并支付检查成本C2及风险损失h3l1kL，施工单位则承受对应的处罚r1P1+r2P2、整改成本(1-l1)I并按比例承担安全风险损失h1l1kL；若监理单位放松监理，则其支付安监单位的处罚r3P3、整改成本r3C1及风险损失h2l2kL，同时获得施工违规的处罚收益r3r1P1，安监单位获得处罚收益r2P2+r3P3并支付检查成本C2及风险损失h3l2kL，施工单位则承受对应的处罚r3r1P1+r2P2，整改成本(1-l2)I及风险损失h1l2kL。

安监单位不检查的3 方收益矩阵如表2 所示。在施工单位合规操作情况下，施工单位仅需支付成本I，而监理单位则需在严格监理时支付监理成本C1，在放松监理时既无支出也无收入；安监单位也无收益和支出。在施工单位违规操作情况下，若监理单位严格监理，则其获得处罚收益r1P1并支付严格监理成本C1及风险损失h2l3kL，安监单位支付风险损失h3l3kL，施工单位则承受对应的处罚r1P1、整改成本(1-l3)I及风险损失h1l3kL；若监理单位放松监理，则其只需支付风险损失h2kL，施工、安监单位也只需支付风险损失h1kL、h3kL。

1.3 演化方程

为直观分析各参与方行为交互演化规律，本文引入社会综合效益这一变量，根据社会综合效益的影响因素及演化规律来探索监管模式效率问题。由表1-2 可得，施工单位是否合规操作的期望收益UY、UN和平均收益-U如式（1）至（3）所示。其中x∈[0,1]表示合规操作的施工单位在全体施工单位中所占比例，y∈[0,1]表示严格监理的监理单位在全体监理单位中所占比例，z∈[0,1]表示实施检查的安监单位在全体安监单位中所占比例。

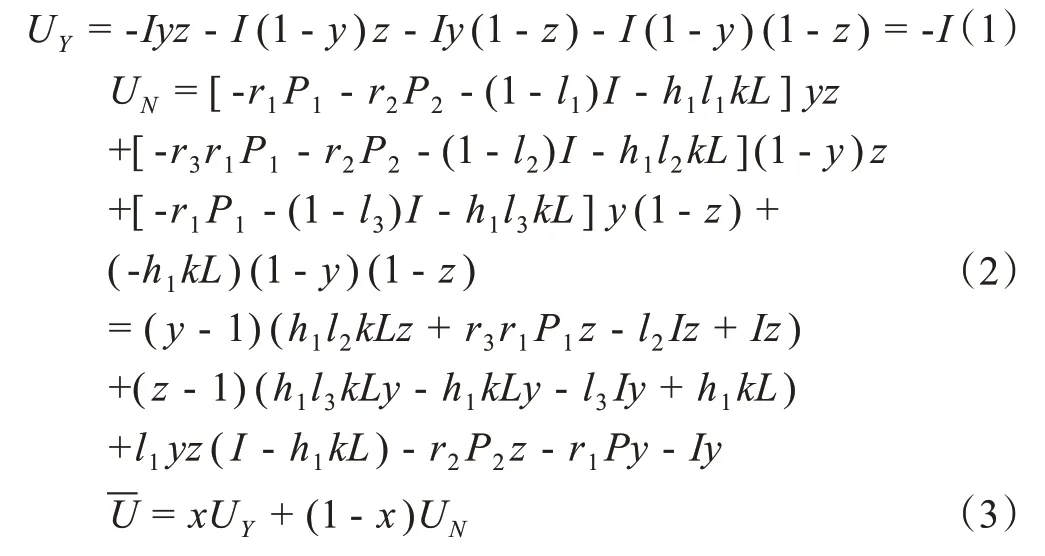
同理，监理单位是否严格监理的期望收益VY、VN和平均收益分别表示为：

安监单位是否实施检查的期望收益WY、WN和平均收益分别表示为：

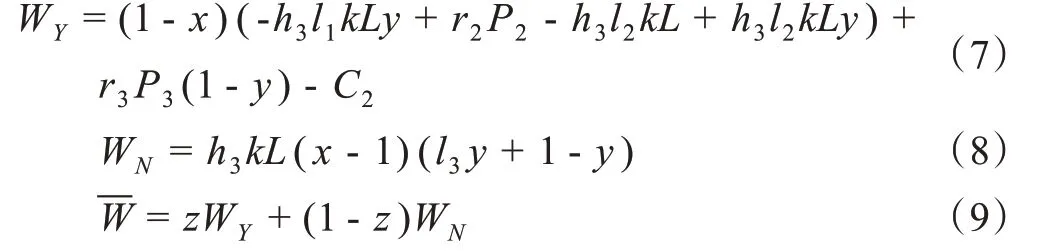
由此可以得出社会综合效益期望收益Π 如式（10）所示。

根据演化博弈非对称复制动态演化方式，得到x、y、z复制动态方程分别为：

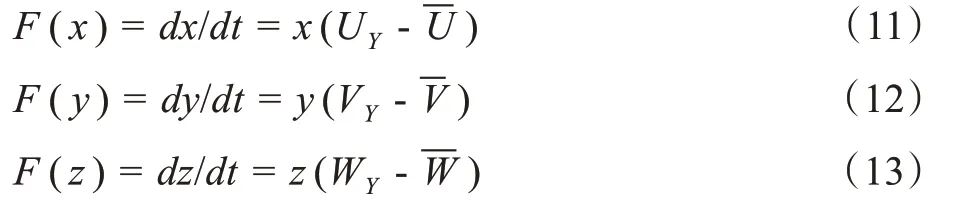
2 仿真分析

现参照上述模型，通过运用matlab 平台进行复制动态演化博弈的数值仿真实验，通过数值仿真技术考察博弈模型中r1、r2、r3、I、C1、C2、L、P1、P2、P3、h1、h2、h3、k共14个参数对三方策略选择和社会综合效益的影响。经测算，将这14 个参数的初始值分别设置为0.5、0.5、0.5、6、2、2、10、3、3、3、1/2、1/4、1/4 和1。其中，r1、r2、r3取0.5 是技术处理，仿真图的上下波动范围都是0.5，有助于观察图形的变化；I、C1、C2的取值是依据现实中三方安全成本的投入确定的。现根据仿真图分析如下：

2.1 单一监管和双重监管的对比

对比图1a 和1b 可知，不论单一还是双重监管，社会综合效益都存在波动现象；且波动形态变化多样。由图1a 变量数值可知，当施工单位合规施工时，监理单位的监管收益小于监管成本，因而逐渐放松监管；而监管的放松降低了施工单位违规成本，从而引发更多违规施工，这又进一步导致事故损失增加，从而提高了监理单位放松监管的成本，促使其严格监管；严格监管的增多又提高了违规施工的成本，最终使得施工单位合规施工，并由此进入下一循环。同理，双重监管下也存在类似现象，只是机理更为复杂。由于该现象涉及至少两方监管主体，且形态多样、关系复杂，本研究将其命名为“复杂监管波动”现象。

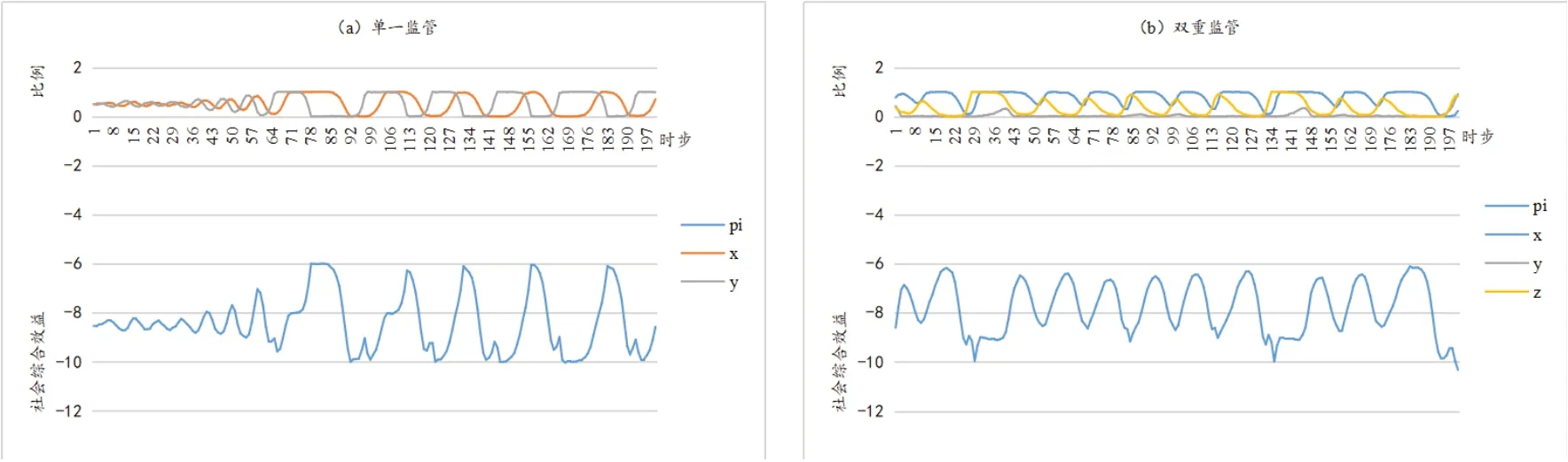
图1 单一监管和双重监管的影响

进一步分析发现，“复杂监管波动”现象包含“小幅震荡波动”和“大幅极值波动”两种形态。以单一监管情况为例，图1a 中社会综合效益曲线在60 时步前为“小幅震荡波动”，60 时步后为“大幅极值波动”。“小幅震荡波动”指博弈方策略选择比例在较小范围内震荡，均未触及0 或1 的极值，社会总效益曲线常规波动。“大幅极值波动”指博弈方策略选择比例大幅变化，达到极值并锁定在极值中一段时间，社会综合效益也不规则地出现一些水平线和变幅波动，称为“极值陷阱”。“极值陷阱”存在的原因可能与复制动态方程有关。复制动态假定群体策略选择的变化速度与选择其他策略的人员比例相关，若其他策略选择人员为0，则无法通过复制来改变策略，只能依靠随机扰动改变策略，因而当出现0 或1 的极值时，其他参数对策略选择的调节可能失效，从而陷入“极值陷阱”。

分析图1b可知，双重监管下施工单位和安监单位交替波动，而监理单位基本处于放松监理状态，表明监理单位和安监单位之间存在明显的替代效应。同时，根据变量数值可知，单一和双重监管下社会综合效益均值分别为-8.41和-7.78，这表明双重监管能在一定程度上提高社会综合效益，但效果有限。

2.2 内部分担比例k的影响（k = 0; k = 1）

对比图2a和2b可知，当k取值为0和1时，社会综合效益均值分别为-10.22 和-7.78，且取值1 时波动幅度较大。结果表明，内部分担比例的降低会导致社会综合效益大幅减少。因此，让相关方切实承担事故责任具有重要意义。然而，人员死亡作为安全事故的典型后果具有不可逆转和无法弥补的特性，导致施工、监理、安监单位不可能完全承担事故责任，“责任有限追索”问题凸显。通过对比还发现，社会综合效益的波动现象与变量取值相关，当变量数值位于某区间时，社会综合效益波动明显，反之则社会综合效益趋于稳定。本文将这种变量取值区间命名为“波动区间”。

图2 内部分担比例k的影响

2.3 3方分担比例的影响(h1 = 1; h2 = 1; h3 = 1)

对比图3a、3 和3c 可知，当h1= 1 时，风险损失全部由施工方承担，施工方保持合规操作，社会综合效益稳定不变，该变量取值位于“波动区间”外；当h2= 1 时，风险损失全部由监理方承担，监理方保持严格监理，但不足以扭转施工方违规操作，社会综合效益稳定不变，该变量取值位于“波动区间”外；当h3= 1 时，风险损失全部由安监方承担时，社会综合效益呈现持续波动状态，该变量取值位于“波动区间”内。进一步变量数值分析可知，h1= 1、h2= 1和h3= 1时，社会综合效益均值分别为-6、-10 和-9.47。由此可见，安全风险损失责任会促进三方重视安全，责任由施工方承担时效率最高。

图3 3方分担比例的影响

2.4 安全风险损失L的影响（L = 0; L = 20）

对比图4a和4b及其变量数值可知，L取值为0时，变量位于“波动区间”内，社会综合效益持续波动，均值为-4.58；L取值为20 时，变量位于“波动区间”外，社会综合效益基本稳定不变，均值为-6.11。同时，可以看到，事故损失提高到20，社会综合效益仅从-4.58 降低到-6.11，降幅不大。可见在施工单位需承担大量事故损失时，其自身不会放任违规行为出现而造成巨大事故损失。

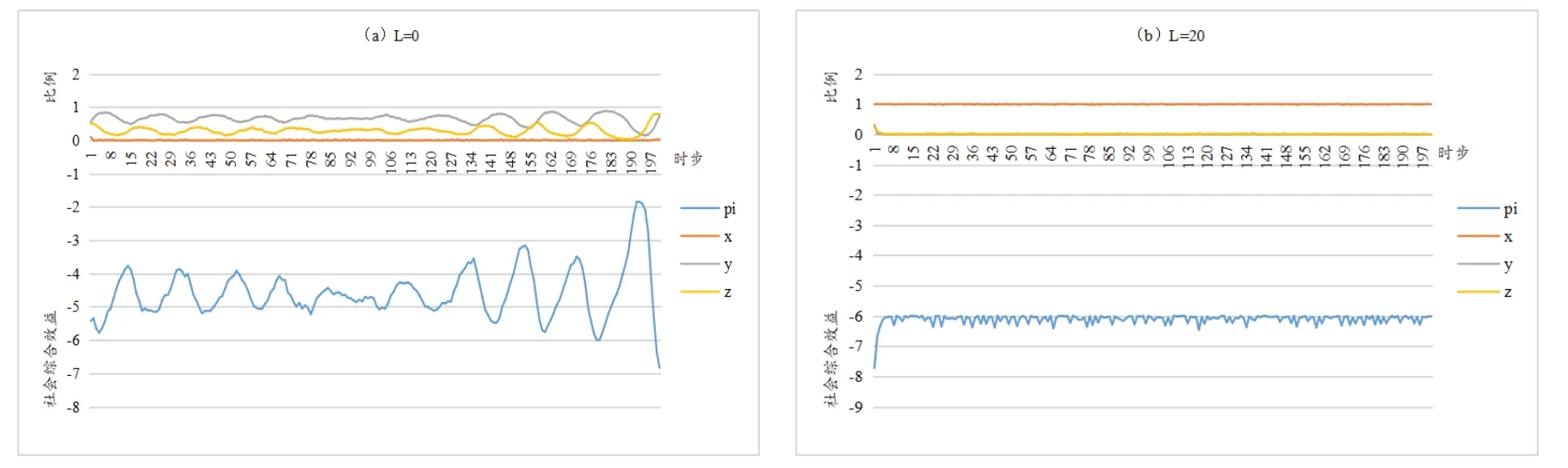
图4 安全风险损失L的影响

2.5 处罚概率的影响

对比图5a 和5b 可知，r1取值0.1 时，变量位于“波动区间”临界值附近，社会综合效益呈现小幅波动状态，均值为-7.96；r1取值0.9 时，存在“大幅极值波动”和“小幅震荡波动”两种状态，社会综合效益均值为-7.59。可见，提高监理单位查处概率，能增加社会综合效益，但也会导致其波动更加剧烈。同理，经数据分析发现，r2取值从0.1 变为0.9 时，社会综合效益均值由-8.94 变为-7.01，且社会综合效益波动减小，可见提高安监对施工的查处概率不仅能增加社会综合效益，还会使其更加稳定。r3取值从0.1 变为0.9 时，社会综合效益均值由-8.69 变为-8.01，可见提高安监单位对监理单位的查处概率，能小幅增加社会综合效益。

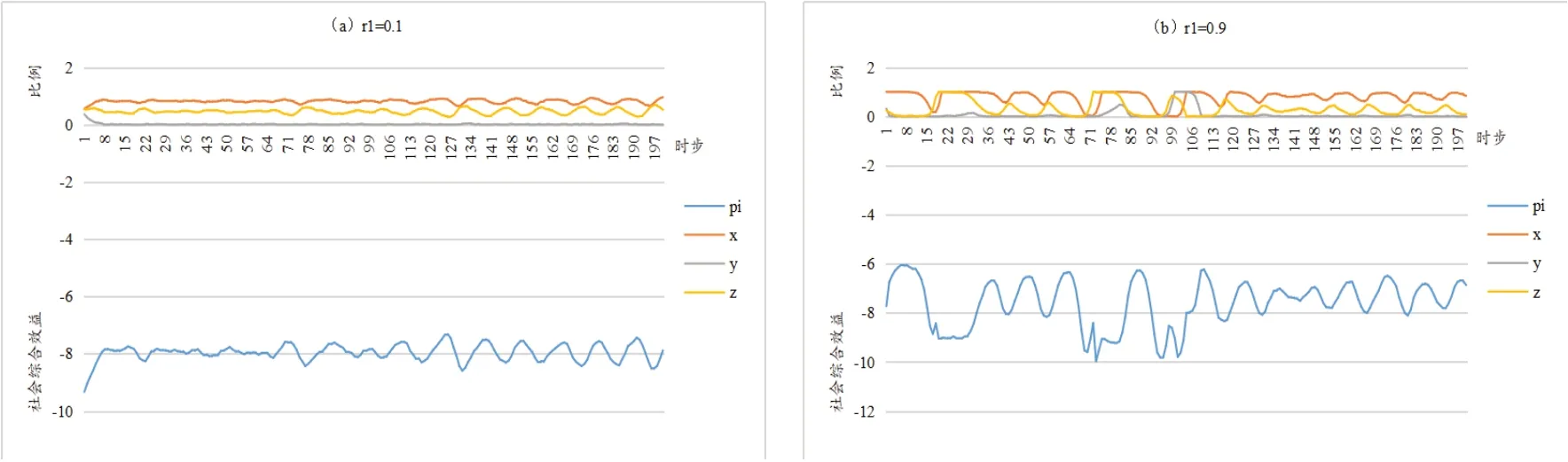
图5 监理单位发现施工单位违规并处罚的概率r1的影响

2.6 处罚力度的影响

对比图6a 和6b 及其变量数值可知，P1取值为0 时，变量位于“波动区间”临界值附近，社会综合效益呈现轻微浮动，均值为-7.92；P1取值为6 时，社会综合效益呈现大幅波动，均值为-7.43。可见，监理对施工的处罚能小幅增加社会综合效益，但也会导致社会综合效益波动加大。同理，经数据分析发现，P2取值0 和6 时，社会综合效益均值分别为-8.73 和-7.43；P3取值0 和6 时社会综合效益均值分别为-8.64 和-7.89。说明安监单位对施工单位、监理单位的处罚能小幅增加社会综合效益。

图6 监理单位对施工单位的处罚P1的影响

2.7 安全成本的影响

对比图7a和7b可知，I取值1和11时，变量取值均位于“波动区间”临界值附近，社会综合效益分别稳定在-1和-14 附近小幅波动，且前者远大于后者。可见，施工单位合规操作成本越低，社会综合效益越大。

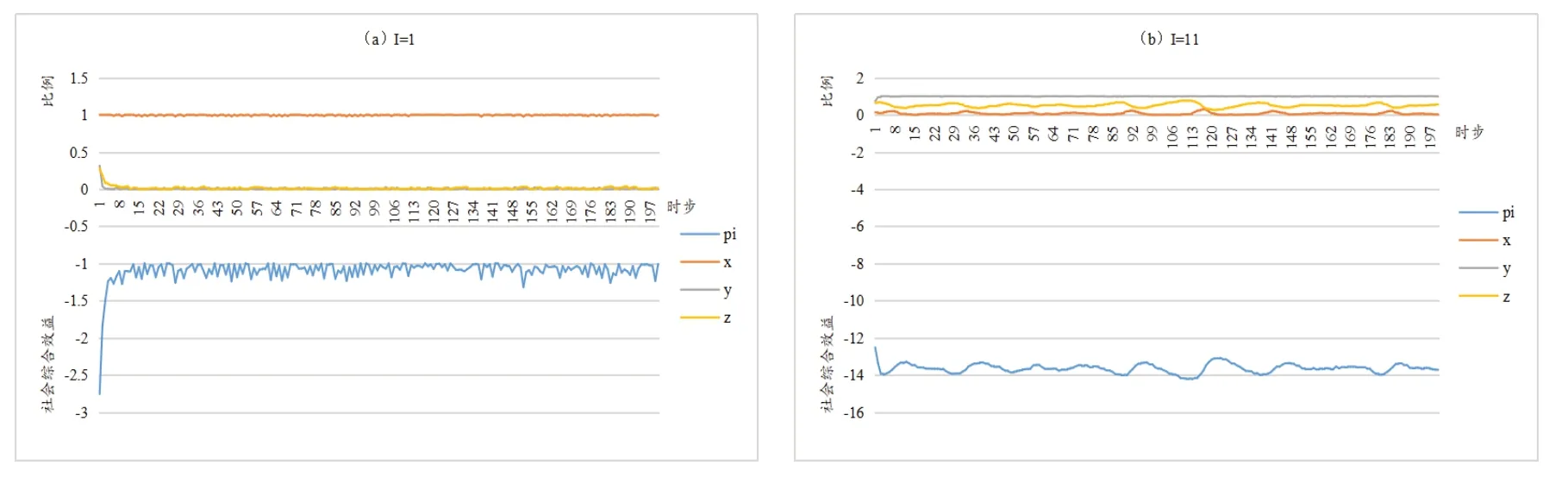
图7 施工单位安全成本I的影响

对比图8a 和8b 及其变量数值可知，C1取值0 时，变量取值位于“波动区间”外，社会综合效益稳定不变，均值为-6；C1取值4时，社会综合效益呈现“小幅震荡波动”和“大幅极值波动”两种状态，均值为-8。可见，监理单位严格监理成本越低，社会综合效益越大。同理，经数据分析发现，安监单位安全成本C2取值0和4时，社会综合效益分别呈现稳定不变和剧烈波动两种状态，且均值分别为-8和-9。可见，安监单位监管成本越低，社会综合效益越大。

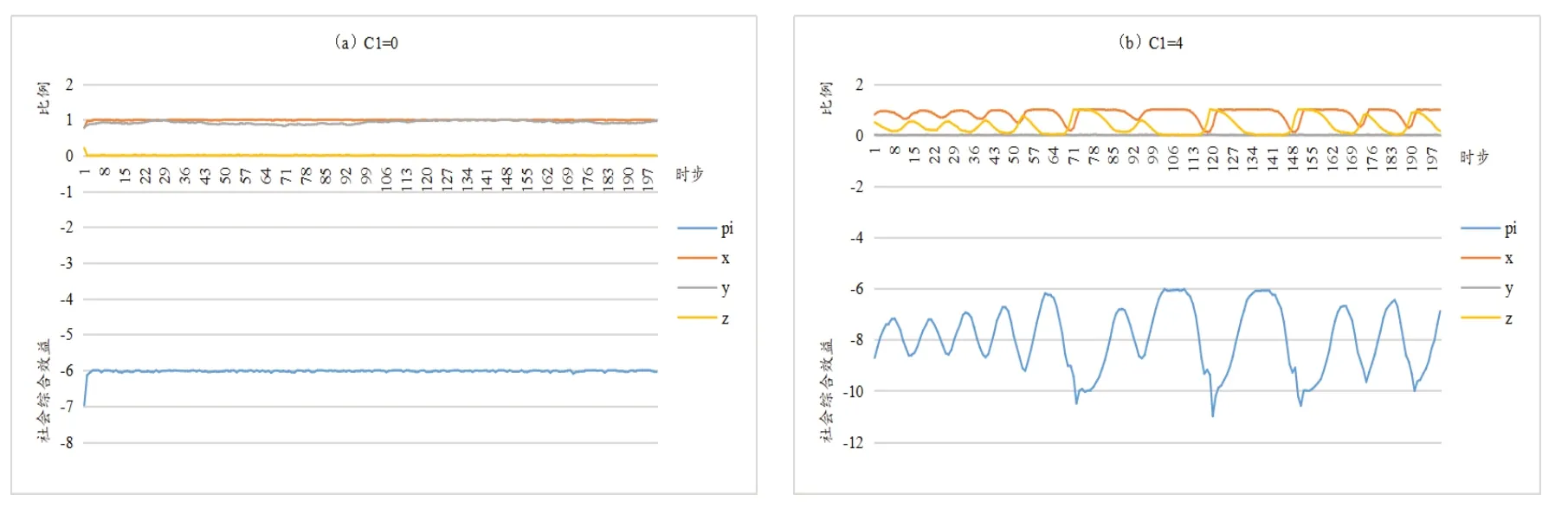
图8 监理单位安全成本C1的影响

3 结论与建议

3.1 结论

（1）影响因素存在“波动区间”，区间内社会综合效益表现出两类波动形态。影响因素取值位于某个“区间”内时社会综合效益表现出“小幅震荡波动”和“大幅极值波动”两类波动状态象，反之则趋于平稳，即影响因素存在一个导致社会综合效益波动的“波动区间”。这意味着，当影响因素取值在波动区间内时，仅依靠当前监管机制无法一劳永逸的解决施工安全问题，“事故增多-监管从严-事故减少-监管放松-事故再增多”的安全监管循环有其深刻的经济学基础。只有让影响因素取值位于“波动区间”外，才可能保证长期安全。

（2）社会综合效益波动的原因在于施工、监理和安监3 者的策略选择及其交互关系，而“极值陷阱”的原因则在于复制动态机制。施工单位受到监理与安监的监管，会随其策略选择而改变策略；而该反应又会促使监理与安监做出策略调整，从而形成施工单位从合规到违规再到合规的往复变化，最终导致了社会综合效益波动。而博弈方比例锁定在极值从而出现“极值陷阱”的原因是，复制动态假定群体策略变化是从选择其他策略的群体学得，若无人选择其他策略，则新策略无从习得，群体策略也就不会变化，从而陷入“极值陷阱”，只能依靠随机突变摆脱。让区域内的施工单位全部陷入安全施工的“极值陷阱”，或可成为保障施工安全的对策之一，但其持续性和可操作性值得商榷。

（3）双重监管与单一监管相比能小幅提高社会综合效益，但效果有限。其原因是监理与安监单位之间存在明显的替代效应。

（4）承担更多安全损失责任会促使相关方更加重视安全，责任全部由施工方承担时社会综合效益最高。然而，由于安全事故致人死亡的特征，安全责任仅能“有限追索”，这也增加了责任落实的难度。

（5）施工单位的风险预期会对安全施工产生重要影响。对于预期风险巨大的工程，施工单位可能主动避免违规操作，反而是预期风险不大的工程，需要重点监管。

（6）提高查处概率和处罚力度均能小幅提高社会综合效益，但同时也可能导致社会综合效益波动加剧。其中安监单位的作用更加显著。

（7）降低合规操作和监管成本能显著提高社会综合效益，同时有助于安全施工。可见，降低合规操作成本非但不意味着在安全投入上“偷工减料”，反而是促进安全施工、提高社会综合效益的重要手段。