Vaughan模型二次电子能谱对空间微波部件微放电效应的影响分析①

张 娜，崔万照，王 瑞，白春江

(中国空间技术研究院西安分院，空间微波技术重点实验室，西安 710000)

0 引言

航天领域的微放电效应是空间微波部件性能退化或失效的一种重要机制[1-2]，其一旦发生将导致谐振类设备失谐、噪声电平抬高、输出功率下降，甚至引发低气压放电，损坏微波部件表面，进而缩短微波部件寿命甚至造成微波部件永久性失效，最终影响通信信道乃至整个微波传输系统彻底失效[3]。

当微放电发生时，空间微波部件，包括多工器、滤波器、开关、环形器、天线馈源等，在真空环境下自由电子经过微波场的加速轰击部件表面，引发材料表面的二次电子发射，这些发射的二次电子在反向微波场的加速下再次轰击部件表面，该过程循环往复，当满足一定条件后，电子将会出现几何级增加，从而形成二次电子倍增过程。该过程中，描述二次电子发射过程的特性参量——二次电子产额(Secondary Electron Yield, SEY)、二次电子能谱(Secondary Electron Spectrum, SES)和出射角分布分别决定了微放电形成过程中微波部件内运动的电子数目、电子从部件表面出射的初速度以及电子出射时的初始方向。

研究表明二次电子发射特性参量对微放电效应有重要影响[4]。Vaughan模型[5]和Furman模型[6]通常被用于描述微放电形成过程及阈值预测中的SEY，Rice[7]比较了这两种模型在预测微波部件微放电阈值方面的一致性，仿真结果表明采用Furman模型的敏感区域范围比Vaughan模型更大，通过改进低能段的Vaughan模型能够得到与Furman模型一致的敏感区域。Buyanova[8]研究了最大SEY对微放电饱和阶段的影响，指出了随着最大SEY增大，倍增过程会从双边放电过渡到单边放电。Seviour[9]通过假定本征和背散射电子的比例，发现背散射电子会增大微放电敏感区域的范围，Semenov等[10]假定出射二次电子速度符合Maxwell分布，指出了在SEY很大时，初速度分布的增大将导致敏感区域的重叠。Mostajeran[11]采用解析的方法考虑了电子出射相位对微放电敏感区域的影响，给出了双平板结构的稳定相位并指出了相位离散将导致敏感区域的增大。Fil等[12]人计算了矩形结构和平行平板传输线微放电阈值对SEY各能量段的敏感性误差。

在空间微波部件微放电仿真中，特别是CST、FEST3D、SPARK3D[13]等仿真软件中，微放电模拟的二次电子发射过程由Vaughan模型或Furman模型描述，Furman模型共包括了41个参数待用户调整，其中SES模型就有22个参数。Vaughan模型由于其精简的数学形式[14]，在实际仿真中受到广泛应用。本文研究了Vaughan模型中二次电子能谱参量对微放电阈值的影响，并对影响规律进行了进一步分析，研究结果对于空间微波部件微放电阈值精确分析具有指导意义。

1 Vaughan二次电子发射模型

Vaughan模型中，SEY计算公式为：

(1)

其中，

公式中，Ep为入射电子能量，θ为入射电子角度，δmax为SEY最大值，Emax为δmax对应的电子能量，Et为截止能量，ks为表面光滑度因子。

二次电子出射能量的概率密度分布，即二次电子能谱SES，它基本符合伽马概率密度函数分布

(2)

其中，Es为二次电子的出射能量，T为材料表面的温度(eV),γ(s,x)表示不完全伽马函数。图 1给出了入射电子为100 eV时，出射二次电子的概率密度函数的曲线，图中横坐标表示了出射电子的能量，纵坐标表示了二次电子相应出射能量的概率。从图1中可以看出，T恰好为SES的最可几能量，即出射电子概率最大的能量。当T增大时，最可几能量向更高的能量段移动，较低能量的电子出射概率降低，而较高能量的电子出射概率增大，当电子能量大于一定值时，该能量下的电子出射概率基本为0。

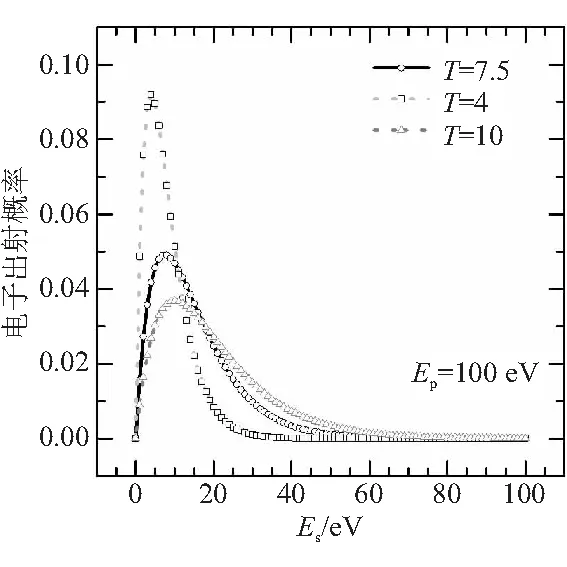
图1 不同γ函数的二次电子能谱

2 二次电子能谱参量对微放电阈值的影响

在讨论二次电子能谱对微放电阈值的影响时，首先需要保证SEY保持不变，本文中微放电阈值仿真时二次电子发射模型的参量为：正入射时Emax=165 eV、δmax=2.22、ks=1、Et=16 eV。本文中的微放电阈值均是采用了多粒子-多碰撞的蒙特卡罗微放电阈值计算方法[15]所得。下面对不同伽马概率密度函数分布的二次电子能谱的微放电阈值进行研究。图 2给出了平行平板传输线中二次电子能谱的伽马函数参量T对微放电阈值的影响。仿真时，平行平板传输线的间隙d=1 mm，传输频率f分别为1 GHz和3 GHz。从图中可以看出，随着二次电子能谱参量T的增大，微放电阈值减小。当f=1 GHz时，T从1 eV增大到10 eV，微放电阈值从48.8 V下降到34.8 V，而f=3 GHz时，T从1 eV增大到10 eV，微放电阈值从315 V下降到170 V，相比于1 GHz，微放电阈值减小的速度越快。

图2 γ函数参量对平板传输线微放电阈值的影响

同样，图 3给出了同轴传输线结构二次电子能量参量对微放电阈值的影响。仿真所选用的同轴传输线内径a=1.54 mm、外径b=3.55 mm，微放电发生的间隙d=2.01 mm，分别计算频率为1 GHz、3 GHz的微放电阈值。与平行平板传输线仿真结果类似，随着二次电子能谱参量T的增大，微放电阈值减小。

图3 γ函数参量对同轴传输线微放电阈值的影响

为了解释二次电子能谱参量T对微放电阈值的影响规律，以f=1 GHz、d=1 mm的平行平板传输线进行微放电阈值仿真，仿真电压选用T=10 eV时的微放电阈值电压34.8 V。统计了50个周期内的所有出射电子能量Eemit和碰撞电子能量Epact的电子数目Ns，并对各种情况的能量分别进行归一化，如图 4所示，(dNs/dEemit)/(dNs/dEemit)max表示归一化的出射电子数目，(dNs/dEpact)/(dNs/dEpact)max表示归一化的碰撞电子数目。

(a) 电子出射能量分布

(b) 电子碰撞能量分布

从图 4(a)中可以看出，出射电子概率最大的能量基本为二次电子能谱的最可几能量位置，这是因为二次电子能谱符合伽马概率密度函数分布，无论碰撞到微波部件表面的入射电子能量取何值，出射电子能量的最大概率位置均为T值。同时，T=10 eV的电子出射能量能谱显著展宽，即具有较高能量的电子数目占比增多，这与图 1所示二次电子能谱分布一致。此外，能谱参量T=10 eV的出射电子的最大能量明显高于能谱参量T=4 eV的状态。这些出射电子经过电磁场的加速后，碰撞到对面极板上，碰撞能量的归一化分布如图 4(b)所示，这些碰撞电子在28 eV能量附近都形成了极大值，而能谱参量T=10 eV的出射电子中较高能量的电子占比更多且最大碰撞能量更高，因而，到达对面极板的碰撞电子中较高能量电子的占比仍然是能谱参量T=10 eV的较多。仿真时由于均选择了Vaughan银材料的SEY模型，当E1=29.6 eV时，SEY=1。能谱参量T=10 eV的碰撞电子比例在E1两侧基本达到了一半，因而该电压是能谱参量T=10 eV的微放电阈值电压，而能谱参量T=4 eV的碰撞电子比例中，低于E1的电子占了较大比例，这些低能量的电子SEY<1，出射电子的个数不断减小，该电压下电子的倍增过程会逐渐熄灭，因此，要想达到放电状态就需要更高的电压，因而能谱参量T=4 eV的微放电阈值电压比T=10 eV的相对更高。

3 结论

本文分析了Vaughan模型中二次电子能谱参量对微放电阈值的影响关系，当符合伽马概率密度函数的二次电子能谱参量T增加时，较高能量的出射二次电子比例增加，在电磁场的加速下，到达微波部件表面的碰撞二次电子能量增加，导致可引起电子倍增的入射电子比例增加，因而微放电阈值降低。二次电子发射特性与空间微波部件的微放电阈值息息相关，准确的二次电子能谱参数选取是精确评估微放电阈值的基础。后续可根据二次电子发射特性测量结果建立典型材料不同表面状态与二次电子能谱参量T的对应关系。