基于砍价活动的行为决策与博弈分析

谭惠琪

电商领域曾被断定不可能再出现独角兽企业，但这一论断早已被一家名为拼多多的企业打破。关于拼多多成功的背后成因，不乏争论的声音。要理解拼多多成功的发生机制，就要从拼多多的企业行为出发，逐步分析，加以论证。拼多多一直以新电商开拓者自称，致力于将娱乐社交的元素融入电商运营。社交性和娛乐性的作用机制是通过各类砍价活动、抽奖、免费领商品等的游戏设置，引导消费者进行活动参与社交分享，从而扩大流量入口，实现用户人数的爆发性增长，引导刺激消费。因此，本文将其社交娱乐性发生作用的逻辑链条应用到具体场景——砍价活动中去，从博弈论的角度解释活动的设置特点和活动效果的成因。考察企业拼多多是如何利用“人”的因素获得成功。

“帮，还是不帮？”——人们在砍价活动中的心理博弈

去年9月，拼多多的百元抢红包大战刷爆了朋友圈。活动的规则是邀请微信好友点击分享链接帮忙砍价，最终砍价成功的人能获得百元现金红包。这场简单粗暴的活动为拼多多创造了巨大的流量，获取了一大批新用户。首先需要明确两点：一是活动的参与者，二是活动的性质。根据年报数据显示，拼多多GMV的63%是由下沉市场贡献。这一定程度证实了活动的发起者与参与者大部分来自下沉市场。依托下沉市场人群具有的熟人型社会、价格敏感属性、闲暇娱乐属性的特征，对砍价的开展形式、奖励金额等元素进行活动设计，使之更贴近人们的日常生活，进而提高参与的可能性。关于活动的性质，则类似于一场心理博弈。纵观活动全程，核心环节就在于参与的裂变，下面将采用博弈模型对此进行分析。在完全信息博弈中，每个参与人都掌握其他所有参与人的特征、策略空间以及支付函数的精确信息，在本案例中，博弈双方具有实际社交关系，因此合理假设他们对彼此的行为特征、策略选择以及可预测的支付函数都具有充分认识。

完全信息静态博弈

1.模型假定

主要假设列于下文：

H1：两个博弈主体，邀请者和受邀者。

H2：参与博弈双方都基于自身利益最大化进行决策选择。邀请方希望顺利完成活动任务，免费获得现金的收益，因此邀请方的策略集合为{邀请，不邀请}；被邀请方则希望不受邀请方的干扰，尽量避免时间精力的损失和人际交往中的情感损失，因此受邀方的策略集合为{帮砍，不帮砍}。

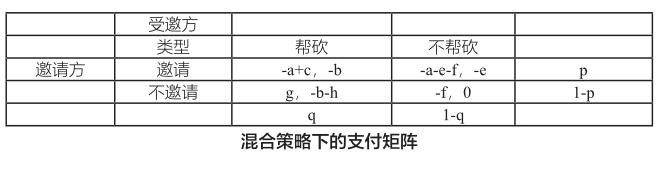
H3：博弈双方在不同的行为选择下的收益和损失存在差异，具体差异呈现如下：

（1）邀请方选择邀请时所需要付出时间和交际成本，损失为a；不邀请时不需要付出成本；（2）受邀方帮忙砍价时需要付出额外的时间或精力成本帮忙，损失为b，不帮忙砍价时没有收益也没有损失；（3）当邀请方发出邀请，受邀方拒绝帮忙时候，双方都会遭受到情感损伤，损失为e，同时，邀请方因邀请失败额外损失f；（4）当邀请方发出邀请，受邀方应约帮忙砍价时候，邀请方因活动成功率上升以及交往过程中获得的满足感，额外收益c；（5）当邀请方没有发出邀请，受邀方也没有应邀参加活动时候，邀请方即为活动参与者因邀请人数数量减少致使活动成功率下降，额外损失f；（6）当邀请方没有发出邀请，但受邀方通过其他渠道得知邀请方参加活动的消息并帮忙砍价，则使邀请方获得额外收益g，受邀方则因信息获得、主动联系等花费时间成本，额外损失h。（a、b、c、e、f、g、h均大于0）

2. 模型分析

根据支付矩阵中各数值大小，分以下两种情况讨论：

当b>e时，根据划线法可以求解受邀方的占优策略是“不帮砍”，此时邀请方的最优策略是“不邀请”，最终的纯策略纳什均衡产生在（不邀请，不帮砍）。这表明了当受邀方付出的成本高于他可能承担的情感损失的时候，受邀方将不会帮忙砍价，那么活动也就无法达成其自身正向传播的目的。因此拼多多抓住具有闲暇时间，对时间沉没成本不敏感的受众群体，同时简化活动参与流程，尽可能将b值减小；另外选择微信、朋友圈的传播途径，让人们选择身边具有亲密关系的朋友进行求助，增加可能的情感损伤e。最终使b

当b

受邀方的期望支付函数为（-b）qp-（b+h）（1-p）q-ep（1-q）=-（b+h）q+（h+e） pq-ep

最优化一阶条件为：（h+e）p-（b+h）=0求解p*=（h+b）/（h+e）

邀请方的期望支付函数为（c-a） qp+gq（1-p）-（a+e+f ）（1-q）p-f（1-q）（1-p）=（c+e-g）qp+（g+f）q-（a+e）p-f

最优化一阶条件为：（c+e+f-g-1） q-（a+e）=0 求解q*=（a+e）/（c+e-g）

因此当邀请方选择（p*，1-p*），受邀方选择（q*，1-q*）时，刚好互为彼此的最优策略，达到纳什均衡状态。因为p*和q*值都必须符合[0，1]的区间，则约束条件为b

3.模型结论

砍价活动以活动参与人数数量和宣传效果为目的，即希望（邀请，帮砍）作为参与双方最大的可能结果，也就是p*和q*值尽可能大。

P*值的大小与额外搜索成本h、时间或精力成本帮忙b和情感损失e相关。e和b对p值的影响在上述讨论b>e的情况时候已做出解释，e和b在满足b

q*值的大小与时间和交际成本a、情感损伤e、收益c、额外收益g相关。q*值代表受邀方选择帮忙砍价的决策概率，当邀请方为邀请这一决策行为付出的时间精力成本越高（a值）以及拒绝邀请方的砍价请求造成自身的情感损伤越大（e值）的时候，邀请方就越有可能帮忙砍价。因此将砍价活动放置于“社交”的情景中，能够提高a和e的数值。当受邀方认为邀请方得到帮助的收益（c值）比较小的时候，出于自身与邀请方决策得失的比较、利他社会因子的影响，会倾向于帮助邀请者进行砍价。

完全信息动态博弈

从动态博弈的视角进一步分析。在动态博弈过程中双方的行为决策存在先后顺序，一方在博弈中的选择作为另一方做出策略选择的前提条件。从现实情况来看，在砍价活动中，邀请双方的决策选择存在着时间差，多数以邀请发作为活动的发起人，实行第一步的行为决策，下面将改变假设，在完全信息动态博弈的一般情形下进行分析。

基于前一个模型假设条件下做一些基本修改：

H4：博弈存在两个阶段，邀请人的决策选择为第一阶段，受邀人的决策选择为第二阶段。

H5：为方便计算，根据上述结论中的得出a，b，c，e，f，h，g大小关系设定具体数值分别为2，3，10，5，4，4，6。

对于先行动的邀请人而言，只要自己选择了“邀请”，理性的受邀人就会选择“帮砍”，所以均衡（不邀请，（不帮砍，不帮砍））是不合理的；而对于受邀人而言，当邀请人选择“邀请”，自己会选择“帮砍”，而当邀请人选择“不邀请”，受邀人显然会选择“不帮砍”，因此均衡（邀请，（帮砍，帮砍））也是不合理的。因此合理的Nash均衡是（邀请，（帮砍，不帮砍）），也就是只有（邀请，（帮砍，不帮砍））的策略选择能达到子博弈精炼纳什均衡。

模型结论

通过两个博弈模型，从理论上证实了拼多多砍价动“引爆性”的合理成因。基于完全信息静态博弈的分析，表明拼多多通过精密的活动设置安排影响人们进行决策行动时的得失，大大提高人们宣传转发、邀请朋友帮忙砍价的概率；接着通过完全信息動态博弈的分析，揭示受邀人在接受邀请人的砍价请求时大多数会选择“帮砍”决策的科学依据。

结 语

本文基于砍价活动的设置安排上，论述了在活动的社交裂变环节中人与人之间的心理博弈。拼多多通过进行对用户的二次身份构建，使潜在消费者摇身一变为社交达人，让人们更主动地为拼多多创造更多的企业价值。这表明，拼多多成功的背后仍然离不开创新，创新了用户的消费体验，重构用户的消费模式，赋予消费者更多选择和主动权，最大程度地实现用户满足。同时启示着其他的电商企业，“人”的因素越来越成为企业创新不可或缺的部分。

（深圳大学经济学院）

参考文献：

[1]陈春霞.行为经济学和行为决策分析：一个综述[J].经济问题探索， 2008（01）：128-132.

[2] 张付安.完全信息博弈下中小企业协同创新路径研究[J].金融经济， 2016，No.428（02）：105-107.