广东省地市级平面独立坐标系的投影变形分析
2021-06-23邓思胜吕鹏军
侯 雪,邓思胜,吕鹏军,陈 敬
(广东省国土资源测绘院,广州510700)
1 引言
城市测绘基准体系是服务国民经济、社会发展、生态文明和国防建设的重要空间基础设施[1]。2008年国务院批准启用2000 国家大地坐标系(缩写为CGCS2000),2018年7月1日起广东省正式启用CGCS2000,CGCS2000 采用国家标准3°带的高斯-克吕格正形投影。在城市测量中,要求长度投影变形不大于2.5 cm/km[2],而采用国家坐标系统在许多情况(高海拔地区、离中央子午线较远地方等)下不能满足上述要求,这就要求建立城市平面独立坐标系,以提高本地区控制基准和测量成果的精度[3]。广东省21 个地级市中,仅有个别地市建立了平面独立坐标系,其他地市都是采用CGCS2000 坐标系的3°带高斯-克吕格正形投影。为控制区域内长度投影变形,需考虑在不能满足区域长度变形要求的区域建立城市平面独立坐标系统,作为该区域统一的、权威的相对独立的平面坐标系统,以满足区域自然资源管理需要,避免重复建设,促进测绘成果共享。
本文综合考虑了区域距离中央子午线的远近,区域地形的差异和区域经度跨度等因素,筛选了东莞市、湛江市、惠州市、韶关市和乐昌市(隶属韶关市)5 个具有代表性的城市进行区域长度投影变形情况的分析。通过结合DEM 数据,在不同中央子午线和抵偿高程面下,对5个区域的高斯投影变形情况进行定性和定量的分析[4],给出了地市建立平面独立坐标系的方案,并对案例分析结果进行了总结,可为广东省各地市平面独立坐标系的建立提供重要的参考价值,同时可为自然资源主管部门在地市平面独立坐标系建立审批时提供参考。
2 理论基础
我国国家坐标系统普遍采用高斯-克吕格投影,先将地面观测值投影到参考椭球面,再将其由椭球面投影至高斯平面。经过以上投影变换引起的长度变形,其大小随投影点与中央子午线及大地水准面的距离不同而变化[5]。在建立有别于国家统一坐标系的城市平面独立坐标系时,投影长度变形值不能大于2.5cm/km(相对误差小于1/40 000)。投影长度变形值的近似公式为:
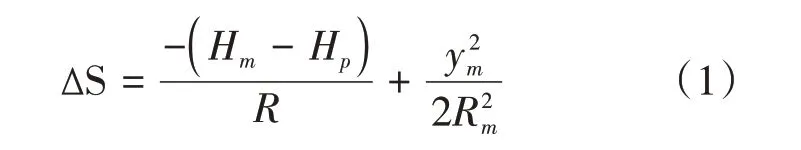
其中,Hm为地面边距离参考椭球面高程的平均值,Hp为抵偿高程面的高程,ym为投影边两端y坐标自然值的平均值,R为该归算边方向椭球的曲率半径,Rm为当地椭球的平均曲率半径,取R≈Rm≈6 378 137m。
当抵偿高程面为0(即Hp=0),根据式1 计算可得投影长度变形值随ym和Hm变化的情况(见表1)。

表1 投影长度变形值随ym和Hm变化的影响(cm)
从表1可以看出,对于不同大地高,都有一个区域,在这个区域内的投影长度变形值小于2.5 cm/km。当测区的平均大地高在160 m以内,在离中央子午线垂距在45 km 内,投影长度变形值能保证小于2.5 cm/km。
3 技术路线
利用DEM 数据成果建立平面独立坐标系的技术路线如下:
(1)选取投影变形分析区域。广东省地势北高南低,北部为由南岭为主构成的山地地区,南部为珠三角平原地区,东西皆以丘陵为主,且城市经度跨度相差较大。结合表1的计算数据,分别选取测区平均大地高小于160 m 和大于160 m、经度跨度小于90 km 和大于90 km 的城市,进行投影变形分析。
(2)选取广东省DEM 数据,裁切出各地市的DEM。本文中所选用DEM 数据集为基于SRTM V4.1 数据经重采样生成,分辨率为1 km,坐标系为国家2000大地坐标系。
(3)求取中央子午线和抵偿高程面的最或然值。计算城市中央经度L0和城市平均高程面高程H平。以L0为初始值,5′为步长,分别向左右取子午线L(取至整5′),以高程每10 m 为步长,计算各个区域在不同中央子午线、不同抵偿高程面的投影长度变形值符合规范要求的比例(以下简称长度变形比)。
(4)结合步骤(3)的计算数据、中央子午线和抵偿高程面的最或然值、区域长度变形比例分布图及本地实际情况确定最佳中央子午线和抵偿高程面,最终确定平面独立坐标系方案。
4 案例分析
为研究不同地形和不同经度跨度区域的平面独立坐标系建立方法,本次实验选取东莞市、湛江市、惠州市、韶关市和乐昌市共5个城市进行研究分析。东莞市位于广东省南部,经度介于113°31′E—114°15′E,东西跨度约75 km,平均高程为39.5 m,为平地地形。湛江市位于广东省西部,经度介于109°31′E—110°55′E,东西跨度约133 km,平均高程为35.8 m,为平地地形。惠州市位于广东省东南部,经度介于113°51′E—115°28′E,东西跨度约166 km,平均高程为168.8 m,为丘陵地形。韶关市位于广东省北部,经度介于112°51′E—114°45′E,东西跨度约195 km,平均高程为414.9 m,为山地地形。乐昌市位于广东省韶关市北部,经度介于112°51′E—113°34′E,平均高程510 m,为山地地形。区域分布见图1。
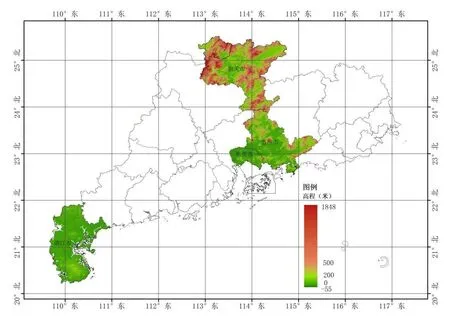
图1 研究区域分布图
经验算分析,得出了5个区域的最佳“中央子午线+高程抵偿面”,并对5 个区域在不同中央子午线和抵偿高程面情况下的长度变形比进行了统计,见图2—图6。
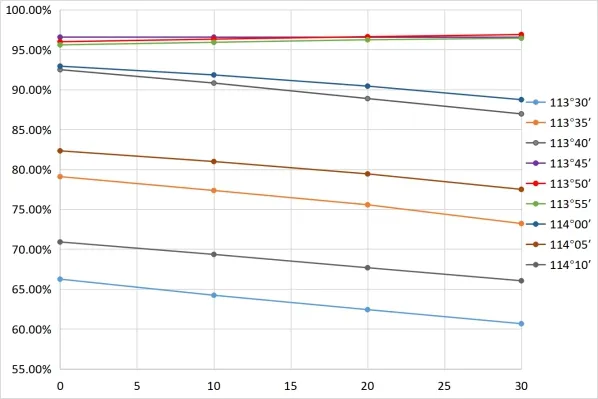
图2 东莞市长度变形比例图

图3 湛江市长度变形比例图
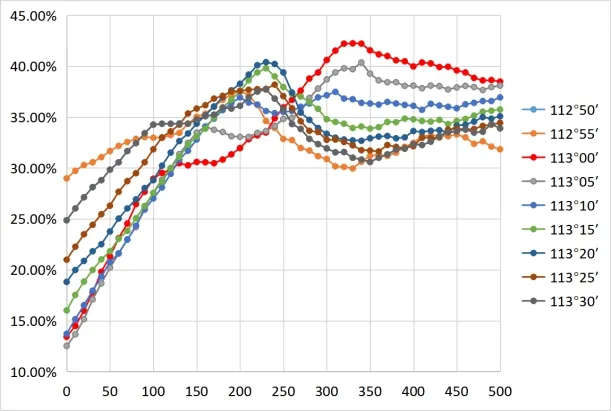
图6 乐昌市长度变形比例图
选取最佳“中央子午线+高程抵偿面”时,5个区域长度变形比分布情况见图7-图11,图中虚线为最佳中央子午线。
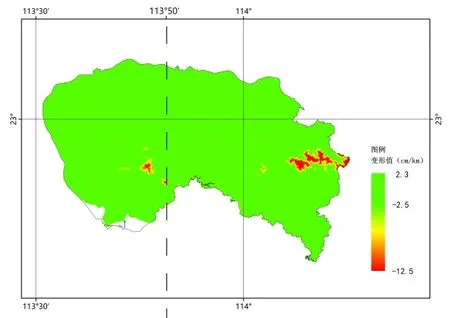
图7 东莞市长度变形比例图
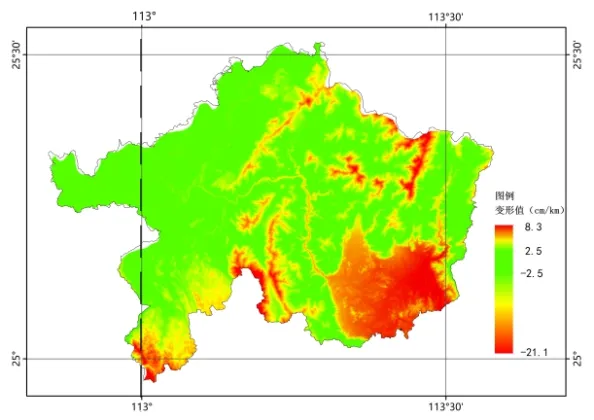
图11 乐昌市长度变形比例图

图4 惠州市长度变形比例图
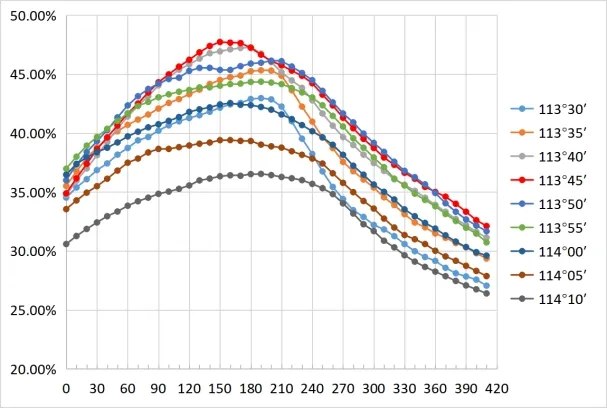
图5 韶关市长度变形比例图

图8 湛江市长度变形比例图

图9 惠州市长度变形比例图

图10 韶关市长度变形比例图
结果显示,当中央子午线为113°50′,高程抵偿面为30 m时,东莞市最佳长度变形比为96.89%,长度变形超限范围基本分布在山地区域;当取中央子午线为114°,高程抵偿面为0 m 时,东莞市长度变形比为92.93%,且长度变形超限范围同样基本分布在山地区域,可见采用国家坐标系可基本满足东莞市的需求。当中央子午线为110°10′,高程抵偿面为0 m 时,湛江市最佳长度变形比为93.15%,长度变形超限范围基本分布在山地区域及位于湛江市边缘的吴川市;当中央子午线为114°35’,高程抵偿面为40 m 时,惠州市最佳长度变形比为71.6%,长度变形超限范围基本分布在山地区域及惠州市边缘的博罗县石湾镇、园洲镇、长宁镇、福田镇,可见采用1个投影带建立平面独立坐标系并不能满足湛江、惠州等经度跨度较大市的要求,建议采用分带投影建立平面独立坐标系,或者考虑以县(区)为单元建立平面独立坐标系。当中央子午线为113°45′,高程抵偿面为150 m 时,韶关市最佳长度变形比为47.73%,长度变形超限范围基本分布在山地区域及位于韶关市边缘的南雄市、乐昌市、乳源县;韶关主城区浈江区和武江区变形基本符合要求,曲江区在山地区域变形不符合要求。当中央子午线为113°00′,高程抵偿面为330 m 时,乐昌市最佳长度变形比为42.25%,长度变形超限范围基本分布在山地区域。可见在韶关、乐昌等地形起伏较大的山地区域,在建立平面独立坐标系时,缩小投影变形区域无法达到更好的投影变形效果,应进一步结合城市范围线,使得在城镇等生产活动较频繁的区域满足投影变形需求更具合理性和操作行。
根据以上的研究分析,可对一个地市的平面独立坐标系建设开展快速评估:
(1)在地势较平坦的平地地形城市,如测区的平均大地高小于160 m,且距离3°标准分带的中央子午线在45 km 内,不需要建立地市平面独立坐标系;
(2)在地势较平坦的平地、丘陵地形城市,如测区的平均大地高小于160 m,投影面可采用国家坐标系参考椭球面;如测区的平均大地高大于160 m,建议投影面采用最佳高程抵偿面。当测区经度跨度不超过90 km,且3°标准分带的中央子午线不从测区中间穿过,建议选择最佳中央子午线来建立地市平面独立坐标系;当测区经度跨度超过90 km,建议采用多投影带来建立地市平面独立坐标系,或者考虑以县(区)为单元建立地市平面独立坐标系。
(3)在地势起伏较大的山地地形城市,建立平面独立坐标系时,应结合城市范围线,选择最佳高程抵偿面作为投影面,并结合城市的经度跨度判断是否采用分带投影,来确定最佳平面独立坐标系的方案,使得在城镇等生产活动较频繁的区域满足投影变形需求,更具合理性和实用性。
5 总结
本文以广东省平地、丘陵和山地地形的5个区域平面独立坐标系建设为例,研究了结合DEM 数据建立平面独立坐标系的方法,并对数据展开了进一步对比分析,总结了不同地形和经度跨度的城市建立平面独立坐标系的建议,在广东省各地市平面独立坐标系的建设中具有重要的借鉴意义,同时可为自然资源主管部门在地市平面独立坐标系建立审批时提供参考。
