基于BP神经网络与多元回归模型对住宅商品房价格进行预测研究

刘杨柏红

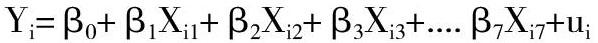
摘 要 伴随着我国经济的发展和国民生活水平的提高，我国房地产市场也在不断发展壮大。其中，住宅商品房作为房地产市场的重要组成部分，对国计民生的影响亦不能小视，引起了国民的高度关注。本文以二线城市-哈尔滨市为例，研究并预测住宅商品房价格的涨幅及趋势。通过利用SPSS对哈尔滨市住宅商品房影响因素进行因子分析，并利用多元回归模型、BP神经网络分别对住宅商品房价格进行预测，将两个模型的预测效果进行对比，选取最优模型，为研究者和需求者提供决策和房价预测工具参考。

关键词 住宅商品房价格 多元回归模型 BP神经网络 房价预测

中图分类号：TP38 文献标识码：A 文章编号：1007-0745（2021）01-0036-05

1 前言

房地产价格的大变革要追溯到1998年国家颁布的《国务院关于进一步深化城镇住房制度改革加快住房建设的通知》，该通知取消了原有的住房分配制度转而施行住房商品化社会化，全国房地产市场迅速发展[1]。2003年国务院发布“18号文件”首次公开肯定了房地产在国民经济发展中的支柱地位[2]。2019年8月，中國人民银行发布公告，提出“住房只住不炒”，进一步施行房贷利率改革，实施贷款市场报价利率[3]。2020年5月，十三届全国人大三次会议提出新定位：“坚持房子是用来住的、不是用来炒的”，与此同时要根据每个城市的特色和不同人群的需求发展相应的房地产事业，促进各地房地产市场平稳健康发展。由此可见，房地产市场和房地产价格受到了大众以及国家的广泛关注。2020年11月，哈尔滨市印发了《关于疫情期间促进我市房地产市场平稳健康发展相关政策的通知》，该通知旨在鼓励房地产企业“卖房”。因此，房地产的健康发展关系到民生，而价格毫无疑问是房地产发展是否健康的重要指标。

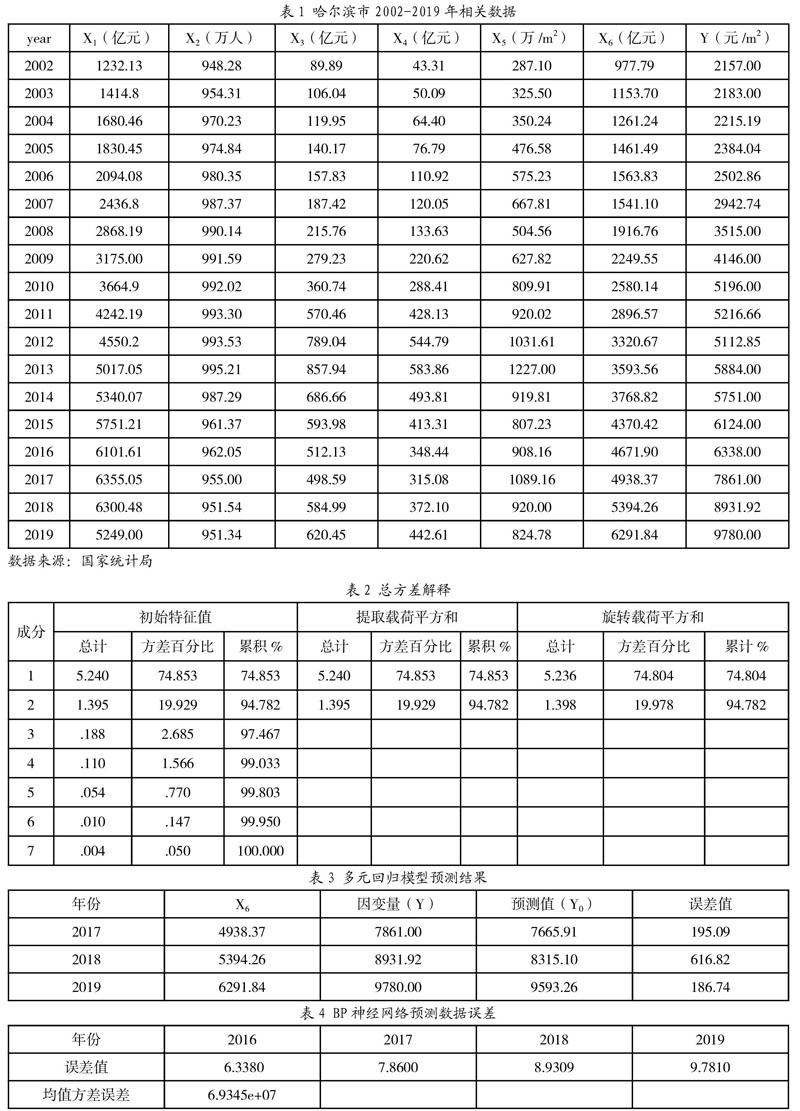
因此，针对住宅商品房价格成倍增长的现象，选取了以二线城市-哈尔滨市为例利用SPSS以及MATLAB工具，进行因子分析，建立多元回归模型和BP神经网络，以研究预测哈尔滨市住宅商品房价格和走势。图1为哈尔滨市住宅商品房价格走势图。

2 国内外研究文献综述

对于房地产价格问题很早就有学者通过构建有效、多样的模型对房地产价格进行进行研究、探讨和预测。国外研究学者很多是通过利用基本经济学原理建立传统线性模型对房地产引发的交易事件进行分析。我国在该领域的研究相对于国外研究来说时间相对晚一些。但是，随着理论与实践研究的深入，我国研究房地产价格变化的学者也越来越多。罗博炜、洪智勇利用python工具基于多元线性回归统计模型对美国部分地区房价进行预测，并对模型进行修正和优化;吴承业、沈逸珺等利用Eviews软件，建立ARMA模型对杭州市房价进行预测，得出房价整体处于较快上升趋势的结果;贾建英利用GM（1，1）模型对唐山市房价进行预测;李秀芝、刘成林等利用马尔科夫链对宜宾市商品房销售价格进行预测，得出宜宾市的房价处于波动状态，上升势头明显;张双妮利用逐步回归模型拟合房价预测模型得出长期来看房价普遍上涨的结论;杨莎莎基于模型平均对房价进行预测和实证研究。通过学习，本文运用多元线性回归与BP神经网络两种工具进行预测，获得准确性更高的房价预测工具。

利用从国家统计局收集到的相关数据进行筛选后，按照年份进行排列。哈尔滨市国内生产总值（亿元）、哈尔滨市年末总人口（万人）、哈尔滨市房地产开发投资额（亿元）、哈尔滨市房地产开发住宅投资额（亿元）、哈尔滨市住宅商品房销售面积（万平方米）、哈尔滨市城乡居民储蓄年末余额（亿元）作为自变量，分别记为X1、X2、X3、X4、X5、X6;哈尔滨市住宅商品房平均销售价格（元/平方米）作为因变量记为Y。表1为哈尔滨市2002-2019年相关数据。

3 基于多元回归模型对住宅商品房价格进行预测

3.1 因子分析

因子分析总的来说就是一种降维的思想，就是将收集到的多个满足真实性和有效性的数据变量转换为几个更具代表性的综合指标，再将相关性相对较高的数据变量组合在一起，以减少因解释变量过多导致深入分析过程变得复杂的现象。

运用因子分析的前提是因子之间存在相关性。因此，在利用SPSS工具对7个变量进行因子分析之前要验证各变量之间的线性关系。本文利用KMO和巴特利特检验方法进行分析。KMO是比较变量间简单和偏相关系数的指标，取值在（0，1）之间。经过KMO检验得出的结果大于0.5，说明该组变量可以进行因子分析;巴特利特检验是计算各个变量之间相关性程度的方法。本文数据检验结果如下：

KMO值=0.736，巴特利特检验显著性 sig=0.000。该结果说明所选取的数据适合做因子分析。

由生成的总方差解释结果表可以分析出：第一和第二主成分初始特征值总计分别为5.240，1.395，两个主成分的初始特征值累计贡献率总共达到94.782%。该比例说明有效信息损失少，通过获取第一和第二个公共因子就能最大限度的解释该组解释变量的整体情况并提供所需要的信息。由于第一主成分的贡献率最大，可以根据第一主成分的数据来判断其他各因素的重要程度：

X1>X3>X4>X5>X6>X7>X2

3.2 多元回归分析模型

利用SPSS对数据进行拟合分析，确定各个因素与因变量之间的关系。建立多元回归分析模型：

本次多元回归利用的是逐步回归模型方法：将每个要进行分析的解释变量单独输入到模型中，每输入一个解释变量后都进行一次F检验，对上一步已经选定的解释变量再逐个进行t检验。若原来输入的解释变量由于后来解释变量的引入变得不显著，则将后者删除，以此来确保最后得到的解释变量集合的检验结果是最优集合。依据上述方法得出哈尔滨市房价的多元回归模型为：

Y=-820.601-0.35*X1+1.130*X2-4.415*X3+4.515*X4+1.829* X5+1.664*X6

整个回归过程进行了一步，进入变量为X6，标准化系数为0.982，得到的德宾-沃森数值为1.035，查表（n=7，k=1），显著性水平为0.016（在0.01左右），因此选择A-1德宾-沃森统计量临界值表中的对应数值，得出=0.435，=1.036。在ANOVA表中，模型sig统计值小于0.05，解释变量系数显著。得出单方程模型为：

将2016、2017、2018、2019年城乡居民储蓄年末余额（X6）带入中，可以得出预测值（如表3所示）。

通过结果可以看出，住宅商品房预测值与实际值存在一定误差并且波动较大，误差仍在合理的预测区间内。

4 基于BP神经网络模型对住宅商品房价格进行预测

4.1 BP神经网络

BP神经网络（Back Propagation）是一种按误差逆传播算法训练的多层前馈网络，人工神经元的研究起源于脑神经元学说，人工神经网络是有大量的简单基本元件——神经元相互连接而成的自适应非线性动态系统[4]。

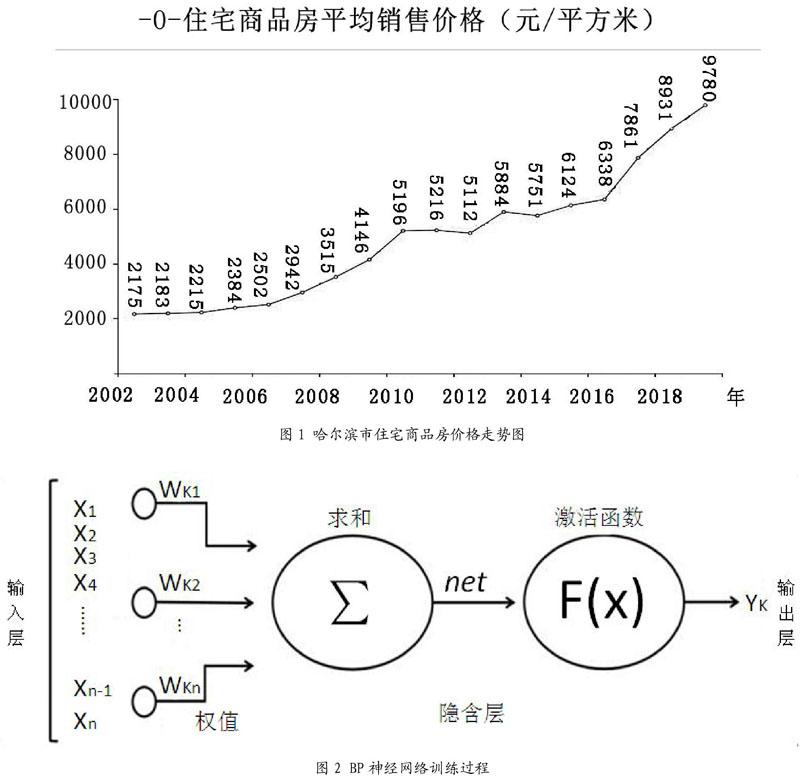
BP神经网络是由输入层（input）、隐含层、输出层（output）组成，首先给网络的各连接權值赋予（0，1）区间内的随机值，也就是我们所说的归一化处理，将输入层对应的数据和图像模式输入给网络，通过计算隐含层中神经元权重的不同，将各神经元权值加权求和，利用激活函数进行非线性运算，得到网络输出结果并与原数据进行比较，从而达到预测数据的效果。

BP神经网络通过对输入的数据进行不断训练，训练结束后输入预测值的自变量从而得到与预测值相近或者与原预测数据相同的数据值并输出。基于BP神经网络的优势，我们利用其作为工具，来完成本文要达到的目的。图2 为BP神经网络训练过程。

4.2 建立BP神经网络模型

4.2.1 数据预处理

在初始建立模型之前，本文使用mapminmax（X）对每一行数据进行归一化处理，将数据统一在[-1，1]的范围之中，可以在一定程度上避免所输入的数据出现不必要的数值问题。在神经网络对于数据训练结束之后，需要再对输出数据进行mapminmax（‘reverse，X，Y）的反归一化处理，将数据恢复成与输入数据相同的形式。

4.2.2 选取神经元节点个数

通过6个影响因素对住宅价格进行预测，建立三层BP神经网络模型，网络输入层节点数n=6，输出神经元n=1，利用Hornik公式可以计算出中间层（隐含层）节点数范围：

R=[（2n+m）1/2，2n+m]，

计算出的中间层神经元节点数范围为[4，13]，再该范围内选择最优的节点数，经过实验，本位选取的最优节点数为8。

4.2.3 训练及预测分析

选取2002-2015年6个自变量数据作为训练数据，sigmoid函数作为激活函数，tansig作为传递函数，训练次数5000次，最小误差10-6。在经过了363次迭代后，误差小于等于10-6时停止训练。

训练数集通过训练，在到达10-6后，曲线变得平缓，并最终落在目标误差线上。训练后的误差（mse）值，最大误差为0.0413，目标误差为1.00e-06，实际误差为9.953e-08。随后以2016—2019年6个自变量数据为基础，通过E计算真实值与预测值之间误差，mse（E）表示均值方差误差值，对因变量进行预测。

通过表4中计算的误差结果我们可以看出，2016-2019年误差逐渐升高，波动较规律，可见预测相近年份的数据准确度更高。从一定程度上预测了与真实值相同的房价走势。

5 影响因素分析

我们可以从图4中观察到，X2（哈尔滨市年末总人口数）从2002年开始一直处于缓慢的下降趋势;X3（哈尔滨市房地产开发投资额）与X4（哈尔滨市房地产开发住宅投资额）走势较为接近。X3随着X3的增长而增长，由于包括哈尔滨市在内的东北地区整体经济增长能力不足，导致在2013年之后X3开始逐步下滑，相应的X4也逐步下滑，由于X3的减少，X5（哈尔滨市住宅商品房销售面积）在2013年达到最高水平后开始下跌。而房X3和X5的减少会影响到住宅商品房市场的供给与需求的失衡;X6（哈尔滨市城乡居民储蓄年末余额）是多元回归模型中提取出的主要因素，在2019年X6急速上涨超过了X1（哈尔滨市国内生产总值），这体现出哈尔滨市居民传统的投资理念：一部分居民将手里的钱用于存款储蓄，另外一部分居民对银行利率不看好，直接将储蓄投资于房地产。存款储蓄多一般情况能反映出现金流量多，货币流通周转速度快，货币创造能力强。但是伴随着X1的下降，产出以及投资减少，居民的储蓄并没有最大效率的实现货币加倍创造的能力，没有达到预期的经济增长水平。住宅商品房价格在各因素的影响下仍在不断升高，除文中提到的六个因素外，还受例如政府调控、国家政策、人均可支配收入、房贷利率等诸多因素的影响，需要进一步进行研究与挖掘。

6 结论

多元回归模型在对住宅商品房价格进行预测时X6（城乡居民储蓄年末余额）对价格影响最大，BP神经网络则是受到不同权重影响因素的影响，相比之下，BP神经网络模型的误差值更小，预测更准确。由于影响住宅商品房价格的因素较为复杂和繁琐，本次研究只抽取六个影响因素的相关数据。因此，对两种模型的学习和比较为今后进行深入研究提供了基础。

参考文献：

[1] 李丹，冷圆，高洪韵.贵阳市商品住房价格影响因素分析及预测[J].现代经济信息， 2019（20）：497-498.

[2] 袁井香.大连商品住宅价格影响因素分析及其走势预测[D].东北财经大学，2010.

[3] 黄燕芬，李志远，张超.坚持“房住不炒”深入推进房地产市场供给侧结构性改革——2017年房地产政策回顾与2018展望[J].价格理论与实践， 2018（01）：18-23.

[4] 吴姗姗.基于BP神经网络的南京市房价预测[J].市场周刊（理论研究），2019（02）：62-64.

（哈尔滨商业大学金融学院，黑龙江 哈尔滨 150000）