基于改进粒子群算法的无人直升机航路规划
2021-06-22王锦博兰庭信盛守照
王锦博,宋 伟,尚 帅,兰庭信,盛守照
(南京航空航天大学自动化学院,江苏 南京 210016)
0 引言
我国西部地区地形复杂,山区众多,易发生山洪、泥石流和地震等突发性自然灾害,灾害发生后,无人直升机能够第一时间深入灾区,到达受灾严重地区进行侦查和救援。由于受灾地区多为山区,不论在进行救援前的灾情调查还是物资运送活动,无人直升机往往需要在山谷之中穿行,为保证无人直升机飞行安全与救援效率,需要快速准确地规划出救援航路。
无人直升机的航路规划需要综合考虑飞行时间、飞行高度和障碍物威胁等,并结合无人直升机的性能约束,规划出一条从初始位置到达任务目标位置的最优航路。常见的无人直升机路径规划算法有Dijkstra算法[1]、A*算法[2]、RRT算法[3]、人工势场法[4],以及以遗传算法、蚁群算法、人工蜂群算法和鸽群算法为代表的智能优化算法[5-9]。将智能优化算法应用在无人直升机路径规划中是当前研究的热点。
粒子群算法(PSO)的基本概念源于对鸟群觅食行为的研究,通过群体中个体之间的协作和信息共享来寻找最优解[10],具有操作简单、算法易于实现和鲁棒性好等优点。PSO算法在初始时能很快向最优值聚拢,但在最优值附近收敛变慢,易陷入局部最优。本文针对无人直升机航路规划问题,对粒子群算法进行了改进,引入选择操作和杂交操作增加种群多样性,避免陷入局部最优,当检测到种群陷入局部最优时,通过变异算子跳出局部最优解。
1 航路规划模型
1.1 无人直升机航路约束条件
基于无人直升机性能限制,无人直升机的航路规划需要满足一定的约束条件。直升机主要约束有最小航段约束、最大转弯角度约束、最大航程约束、最小离地高度约束和最大爬升角约束等。
a.最小航段约束定义为无人直升机改变飞行姿态前必须保持稳态前飞的最小距离。在飞行过程中频繁改变姿态会影响无人直升机的稳定性,严重时会导致坠机事故,所以应尽可能避免频繁的姿态变换。则此约束为
li>lmin
(1)
li(i=1,2,…,n)为无人直升机第i个飞行航迹段长度;lmin为最小航迹段长度。
b.最大转弯角度约束定义为无人直升机在水平面内做圆周运动时的航向连续变化最大范围。山谷大气环境复杂,做大角度转弯时,无人直升机极易受到山谷风影响,所以需要限制无人直升机的连续转弯角度。则此约束为
ψi<Δψmax
(2)
ψi(i=1,2,…,n-1)为无人直升机第i个转弯角度;Δψmax为最大转弯角度。
c.最大航程约束定义为无人直升机在飞行过程中由于携带的燃料限制或特殊任务要求,飞行航线的长度必须满足小于或者等于1个预先设置的最大值。则此约束为
(3)
Lmax为最大航程。
d.最小离地高度约束定义为无人直升机在飞行过程中避免与地面相撞,必须满足最小飞行高度。则此约束为
hi≥hmin
(4)
hi(i=1,2,…,n)为第i段航段最低离地高度;hmin为要求最小离地高度。
e.最大爬升角约束定义为直升机在规划的航迹时需要限制爬升和下降的角度。则此约束为
(5)
θmax为直升机最大爬升角;|zi-zi-1|为第i段航迹的高度差;ai为第i段航迹的水平投影长度,i=1,2,…,n。
1.2 航路代价函数
在规划航迹时主要考虑时间代价与威胁代价,并规划出一条能够安全、快速到达指定任务地点,满足所有约束条件的可用航迹。无人直升机在山谷中飞行时,为了保证飞行安全,通常采用经济巡航速度执行任务,保证最大剩余可用功率,能够及时应对突发情况,所以时间代价可以转化为航程代价。为了保证飞行过程平稳,还需考虑高度代价。设F为每条选出航迹的代价函数:
(6)
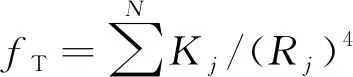
在进行个体适应度计算时,必须先对航迹代价函数中的各部分代价值进行归一化处理,避免各部分代价值数量级差异导致的计算误差。
2 基于粒子群算法的无人直升机航路规划
2.1 标准粒子群算法
标准PSO算法中,每个粒子仅有速度和位置2个属性,粒子通过跟踪个体最优解Pi和种群最优解Pg实现全局寻优,迭代中粒子的速度和位置更新公式为:
vi(t+1)=w×vi(t)+R1c1(Pi-xi(t))+R2c2(Pg-xi(t))
(7)
xi(t+1)=xi(t)+vi(t+1)
(8)
vi∈[vmin,vmax]、xi∈[xmin,xmax]分别为第i个粒子的速度和位置;R1和R2为0~1之间的随机数;ci和c2为加速常数,表示粒子受个体认知和社会认知的影响程度;w为惯性权重因子,当w较大时,算法具有较强的全局搜索能力,w较小则算法倾向于局部搜索。一般是将w初始化为wmax,并使其随迭代次数的增加线性递减至wmin。w的线性变化由下式确定:
(9)
tmax为最大迭代次数;t为当前迭代次数。
2.2 改进粒子群算法
标准PSO算法通过粒子间的信息交流完成全局寻优。当粒子个体陷入局部最优时只能通过其他粒子才能逃脱。迭代后期种群会呈现趋同性,搜索能力变差,容易陷入局部最优解,从而导致PSO算法无法找到全局最优解。
为了避免PSO算法中的粒子失去种群多样性,在迭代过程中引入选择操作和杂交操作。
采用轮盘赌的方式从群体中选取一部分粒子,记为子群D,个体的选择概率与其适应度值成比例,即
(10)
fi为粒子个体适应度。
将子群D中的粒子随机的两两杂交,产生同样数目的子代粒子代替父代粒子。子代位置由父代粒子位置进行杂交产生。
xs=CR×xp(1)+(1-CR)xp(2)
(11)
xp为父代粒子位置;xs为子代粒子位置;CR=rand(0,1)为杂交算子。
子代速度由下式计算:
(12)
vp为父代粒子速度;vs为子代粒子速度。
当连续几代的全局最优适应值不变,认为种群陷入局部最优,此时随机选取3个粒子,对粒子群进行变异操作,则有
xi=xl+F(xm-xn)i≠l≠m≠n
(13)
xl、xm、xn为随机选取粒子位置;F为差分变异算子。
2.3 算法流程
无人直升机的飞行轨迹可定义为一系列有序的三维空间位置点的集合{PS,P1,P2,…,PG},PS、PG分别是无人直升机的起始位置和目标位置,Pi=(xi,yi,zi)(i=0,1,2,…,n-1)为中间航路点,相邻的空间位置之间使用直线连接。在三维空间中进行随机搜索非常复杂,由于某点地面高度与该点纵横坐标有直接关系,所以可以将搜索空间降维到二维空间,再按照改进PSO算法步骤进行搜索,减少搜索时间。
改进PSO算法的具体步骤如下:
a.将搜索空间沿x轴方向n等分(对应n-1个中间航路点)。设置算法基本参数,包括群体规模N、最大迭代次数tmax、最大惯性权重wmax、最小惯性权重wmin、加速因子c1和c2、变异算子F等。
b.初始化粒子群位置矩阵,计算初始个体适应值,并将最好个体适应值记为初始全局最优适应值。
c.根据式(7)和式(8)更新粒子群位置和速度,并将其限制在速度与位置范围内。
d.比较每个粒子适应值与其历史个体最优适应值,如果优于历史个体最优适应值,则更新Pi。将所有个体最优适应值与全局最优适应值比较,更新Pg。
e.通过轮盘赌的方式,从种群中选择一部分粒子按照式(11)和式(12)进行杂交。
f.判断算法是否达到终止条件,是则转步骤h,否则,进入步骤g。
g.判断是否陷入局部最优,若是则根据式(13)进行变异,转向步骤d,否则,转向步骤c。
h.输出航路种群中最优的航路作为航路规划结果。
3 实验结果及分析
在MATLAB 2017b环境下,分别使用标准粒子群算法PSO-1和改进粒子群算法PSO-2进行了仿真验证。粒子群算法的参数设置:PSO-1和PSO-2的种群数量N=30,最大迭代次数tmax=500,惯性权重因子wmax=0.9、wmin=0.4,加速常数c1=c2=2,PSO-2的变异常数F=0.15。设置性能指标的权重系数分别为w1=w2=w3=1/3。 适应度值变化曲线图1所示。

图1 适应度值变化曲线
由图1可知,改进粒子群算法在第86代就已经收敛到最优,其收敛精度和收敛速度都优于标准粒子群算法,表明改进PSO算法能够快速有效地为无人直升机进行任务航路规划。
图2和图3分别是改进粒子群算法优化得到的无人直升机三维最优航路和二维等高线航路。可以看出,基于改进粒子群算法得出的最优航路成功地规避了所有障碍威胁,航路平滑且精度较高,满足无人直升机性能约束,保证了飞行的安全性。
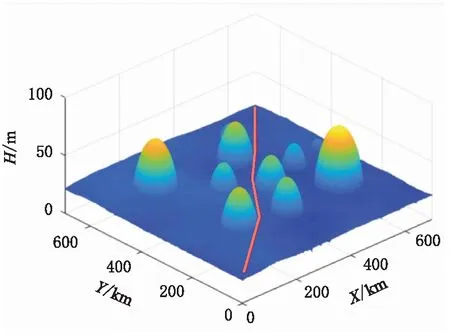
图2 三维航路图

图3 等高线图
4 结束语
针对传统PSO算法易陷入局部最优的缺点,引入选择、杂交、变异操作,对粒子群算法进行改进。仿真实验结果表明,本文所提出的改进PSO算法能合理有效地规划无人直升机航路,并迅速地得到无人直升机的最优航路。
