基于MUSIC及其改进算法的DOA估计研究*

姚昕彤，王玉文，刘 奇，金 硕

（电子科技大学，四川 成都 611731）

0 引言

根据无线电波的传播特性，使用仪器对无线电波到达的方向进行测量和确定的过程叫做无线电测向[1]。测向方法有多种，在这些算法中，基于空间谱估计的测向算法因具有高分辨力、高准确度等优点而被广泛应用。多重信号分类[2]（Multiple Signal Classification，MUSIC）算法是一种典型的空间谱估计技术。该技术的出现使得空间谱测向技术发展进入了新的台阶。然而，该算法也存在一些不足。例如，在低信噪比、小快拍数条件下，MUSIC 算法的分辨力降低，估计性能显著下降。在多径环境中，由于信号之间高度相关，MUSIC 算法失效。针对以上两个问题，本文在传统MUSIC 算法的基础上进行改进，提出了一种新的测向算法。新算法解决了传统MUSIC 算法低信噪比、小快拍数条件下分辨率低的问题。通过将改进后的MUSIC 算法与空间平滑技术结合，还可以用来解决相干信号的空间谱估计问题。

1 经典MUSIC 算法

MUSIC 算法被广泛地用于空间谱测向技术，算法步骤及原理如下。假设有K个远场窄带信号，从不同的方向θ1,θ2,…,θk分别射入M个阵元的均匀线阵，如图1 所示。该均匀线阵采用半波长布阵，信号与线阵法线之间的夹角θk∈[-π/2,π/2]。在该环境中，噪声服从均值为0、方差为σ2的高斯分布，与信号不相关。均匀线阵接收到的数据可以用式（1）描述为：

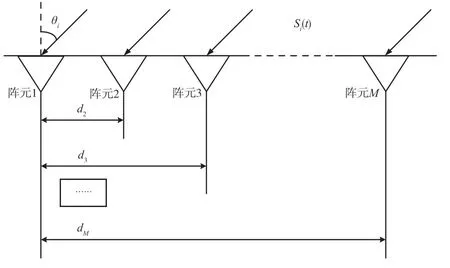
图1 均匀线阵

式中：t=1,2,…,T为信号采样的次数，也叫做快拍数；x(t)=[x1(t),x2(t),…,x M(t)]T是均匀线阵所接收的数据向量，每个向量中有M个元素，表示x(t)为M维向量；噪声向量N(t)=[n1(t),n2(t),…,nM(t)]T同样为M维；空间信号向量S(t)=[s1(t),s2(t),…,sk(t)]T为K维；A(θ)=[a(θ1),a(θ2),…,a(θk)]为导向矢量矩阵，是M×K维。在矩阵A(θ) 中，有K个导向矢量α(θ)。α(θ)包含角度信息，且在理想情况下，表达式为：

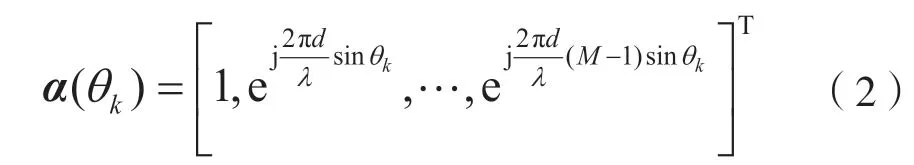
阵元接收到的信号的自相关矩阵为：

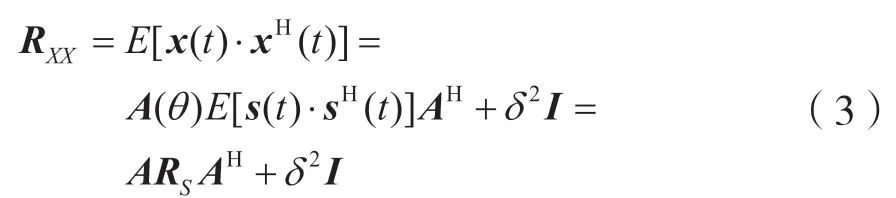
式中，参数δ2为噪声的功率，参数I为单位矩阵，Rs为信号的协方差矩阵。

获得自相关矩阵Rxx后，对其特征分解可以得到Rxx的特征值λ。若特征值λ有M个，则将M个特征值从大到小排序为：

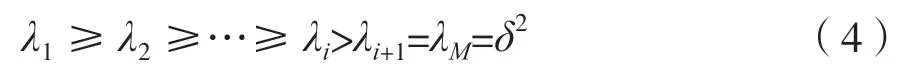
在M个特征值λ中，有i个特征值较大的信号特征值以及M-i个λ较小的噪声特征值。由噪声和信号的特征值，可以计算得到噪声特征值和信号特征值所对应的特征向量，即可得到互相正交信号子空间ES=[e1,…,ei]与噪声子空间EN=[ei+1,…,eM]。记GN为所有噪声的特征值所对应特征向量组成的矩阵。由信号源之间相互独立时，ES=[e1,…,ei]与EN=[ei+1,…,eM]正 交，且α(θ)也 与EN=[ei+1,…,eM]正 交，所以可以得到导向向量α(θ)与矩阵GN之间的关 系为：

由此得到MUSIC 算法的空间谱函数：

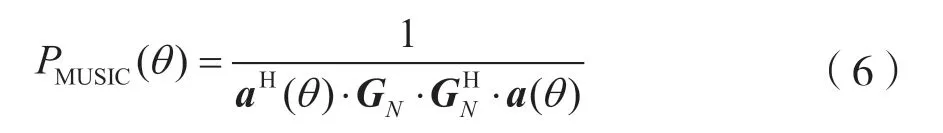
在得到空间谱函数PMUSIC(θ)后，扫描空间谱函数的谱峰，便可以得到波达方向的估计值。但是，在实际中，均匀线阵所接收的数据有限，可以使用相关矩阵的估计代替R进行特征分解。在实际情况中，由于噪声的干扰使得导向向量α(θi)与噪声子空间并不严格的正交，所以式（5）并不严格等于0，而是一个极小值，故MUSIC 算法中空间谱函数的公式可以变为：

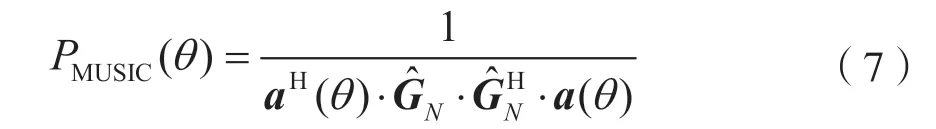
总结以上过程，可以得到MUSIC 算法进行波达方向估计的步骤：

步骤1：由式（3）得到阵元接收到的信号的自相关矩阵Rxx；

步骤2：将Rxx进行特征分解，得到相应的特征值λ，并将特征值从大到小排序；

步骤3：根据式（5）和式（6）得到空间谱函数，扫描空间谱函数的谱峰，得到波达方向的估计值。

2 改进MUSIC 算法

在传统的MUSIC 算法中，需要利用多个天线来接收数据阵列，使用大量数据来估计信号的协方差矩阵。在大快拍数、高信噪比、天线阵元个数充足的条件下，MUSIC 算法能够充分发挥作用，获得较高的分辨率。但是，在实际的DOA 估计场景中，往往达不到上述快拍数大、信噪比高、天线阵元个数充足的理想情况，使得MUSIC 算法对阵列协方差矩阵的估计有较大的偏差，且会导致特征分解自相关矩阵得到的噪声和信号特征值之间的差异减弱，从而使得算法的性能显著下降。如果两信号以较小的角度间隔入射均匀线阵，MUSIC 算法的分辨性能会明显降低。针对以上问题，在传统MUSIC算法基础上提出了一种新的空间谱函数估计算法。根据实际的DOA 估计场景，修正噪声子空间的加权系数，得出新的噪声子空间，再结合经典MUSIC算法的空间谱函数步骤，得到改进的伪谱函数。改进噪声特征值具体的计算方法如下：

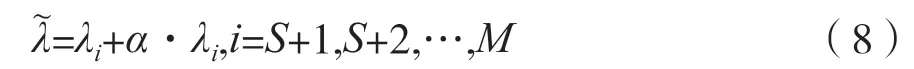
式中，λi为初始噪声的特征值，为新的噪声特征值，α为校正值。

噪声子空间中，每个特征值所对应的特征向量对空间谱函数的贡献度有所不同[4]。在小快拍数、低信噪比的条件下，可以通过调节校正值α来影响发散信号的发散程度，且α不会影响信号方向矢量，从而可以确保有稳定的信源数估计。校正值α的取值也会影响算法的性能。如果校正值α过大，会导致特征分解自相关矩阵得到的噪声特征值与信号特征值之间差距过小，分辨率不明显，从而引起欠估计的问题。校正值α太小，会造成抑制噪声作用减弱。若α=0，则新算法与传统的MUSIC 算法相同。所以，需要寻找合适的校正值α。

根据信息论准则，在可以估计出信源数的条件下，从大量的实验中总结出噪声特征值的最大值与最小值之比应小于2[5]，即：

改进后的特征值求解步骤具体如下。

（1）将自相关矩阵Rxx进行特征分解，得到相应的噪声特征值，并对噪声特征值按照从大到小顺序排列。

（3）令α=0.1×p，得到最终校正值α。

（4）得出新的噪声子空间形式：

3 相干信源空间谱估计

提出的基于MUSIC 算法的改进型DOA 估计算法，解决了传统MUSIC 算法在低信噪比、小快拍数条件下分辨力低的问题，能应用于更广泛的测向场景。但是，算法假设信号源之间都是相互独立的，而如果入射到线阵列的信号是相干信号时，改进的测向算法也将同其他DOA 估计算法一样，将由于无法分辨出相干信号而失效。因此，在改进型MUSIC 算法基础上，结合空间平滑技术，提出了相干信号的DOA 估计方法。相干信号的DOA 估计方法如下：假设K个来自θ1,θ2,…,θk方向的信号为相干信号，先使用空间平滑技术对均匀线阵接收的信号进行去相干的处理，后使用提出的改进型MUSIC算法对预处理后的数据进行分析和估计，最终得到相干信号来波方向的估计值。

空间平滑（Spatial Smoothing，SS）[6]技术可以用于处理相干信号，先将均匀的线阵列划分为多个叠合子阵列，每个叠合子阵列具有相同阵列流型。再计算各个子阵列的协方差矩阵，最后将各子阵列的协方差矩阵进行平均处理，达到去相干的效果。

假设K个相干的信号Sk(t)以不同的方向角θi进入到M元的均匀线阵上，阵元之间间距为d，声速为c，波长为λ。根据空间平滑算法处理相干信号的步骤，先将均匀线阵分为L个叠合的子阵，其中每个子阵包含N个阵元。L和N满足以下关系：

前向空间平滑和前向空间平滑原理，分别如 图2 和图3 所示。

图2 前向空间平滑原理

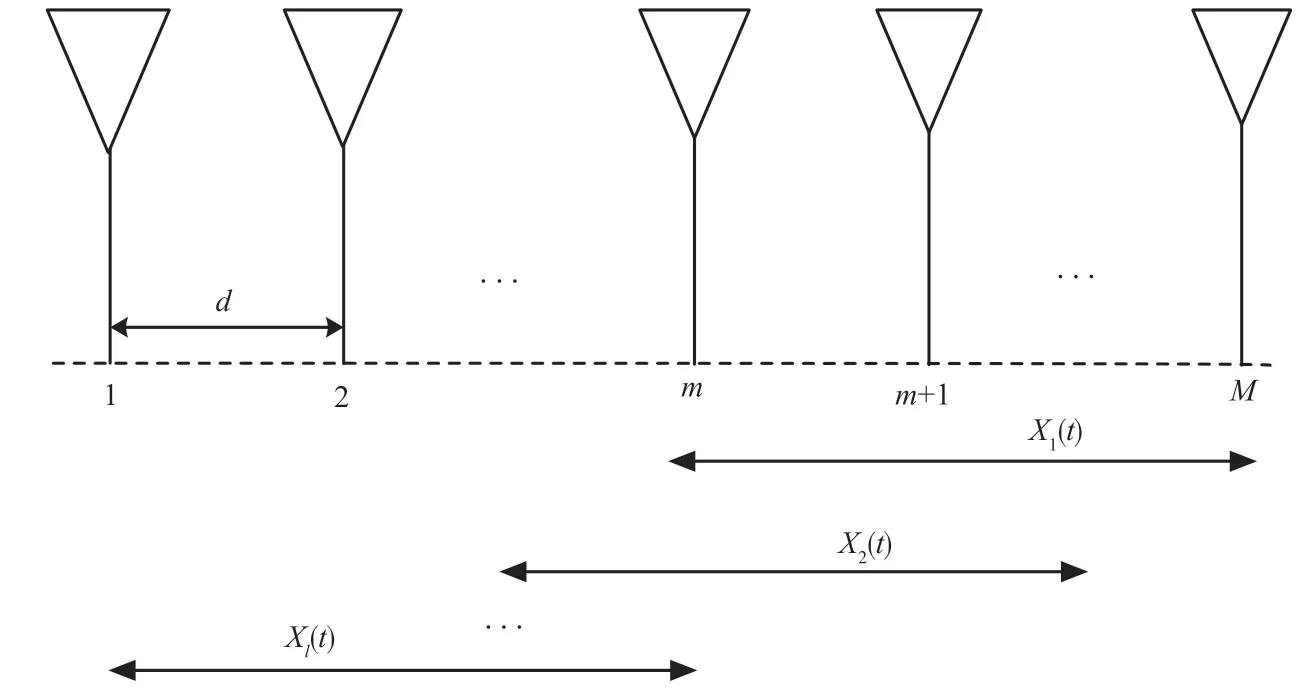
图3 后向空间平滑原理

如图2 所示，前向空间平滑（Forward Spatial Smoothing，FOSS）是从阵列的第一阵元开始划分。第l个子阵的接收数据矢量可以表示为：

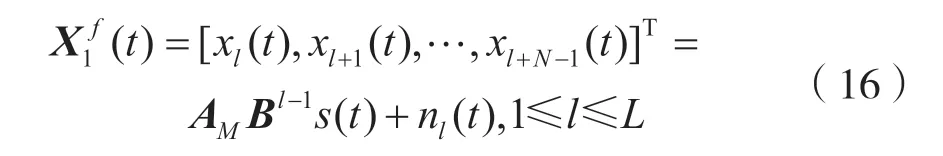
式中：AM为N×K维方向矩阵；AM列为N维的导向矢量aM(θi),i=1,2,…,k；第l个前向子阵的噪声矢量定义为nl(t)，其阵列的协方差矩阵为：

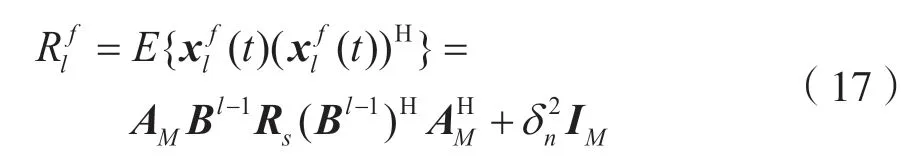
使用前向空间平滑技术处理后的协方差矩阵为：

后向空间平滑是从直线阵列最后一个阵元向第一个阵元平滑，得到后向空间平滑的协方差矩 阵Rb：

由于各个平滑子阵的阵元是相同的均匀矩阵，因此矩阵Rb是矩阵Rf的共轭倒序阵，可以用表示前后向平滑协方差矩阵，则之间的关系式为：

前后向空间平滑技术利用了前向平滑和后向共轭倒序不变的性质[7]，通过将各个子阵列协方差矩阵的总和求平均来替代原MUSIC 算法中的Rs。该算法可以检测到2M/3 个相干信号，可以有效处理相干信源协方差矩阵的秩亏缺问题，使得信号源个数同协方差矩阵的秩相等[7]。

将前后向空间平滑技术与改进型MUSIC 算法相结合，得到相干信号的DOA 估计新方法。

新方法步骤如下。

步骤1：建立阵列数据的接收模型，将M阵元的天线阵分为L个相互重叠的子阵。每个子阵的阵列流形保持一致，根据式（17）求出子阵列协方差矩阵。

步骤2：使用式（18）计算得到矩阵Rf；根据式（19），可以得到矩阵Rb；在获得矩阵Rf和矩阵Rb后，可以由式（20）求出前后向平滑协方差矩阵。

4 仿真结果及分析

4.1 实验1：MUSIC 算法的谱函数图像

假设信号源为两个不相干且波长为λ的窄带信号，分别以2°和6°的方向入射到阵元数为10、阵元间距为λ/2 的均匀线阵上。信号与噪声之间保持相互独立，其中噪声为高斯分布，信噪比为0 dB。快拍数为60。图4 为MUSIC 算法的谱函数图像。

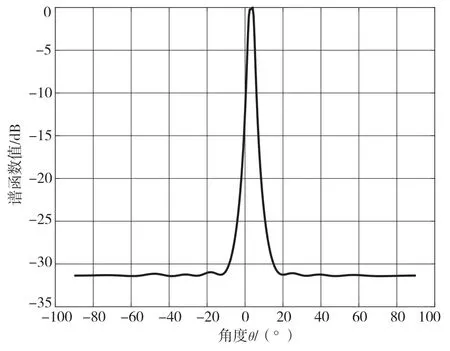
图4 MUSIC 算法的谱函数图像

4.2 实验2：改进MUSIC 算法的谱函数图像

与实验1 相同，同样假设信号源为两个不相干且波长为λ的窄带信号，入射到阵元数为10、阵元间距为λ/2 的均匀线阵上。其中，噪声为高斯分布，信噪比设置为0 dB，快拍数设置为60。图5 为改进MUSIC 算法的谱函数图像。

从图4 可以看出，在低信噪比、小快拍数的背景下，经典MUSIC 算法无法分辨出两个相邻入射角，MUSIC 算法在该场景下失效。而在图5 中，改进型MUSIC 算法能够明显看出两个相邻入射方向信号的谱函数峰值，便可以估计两个入射信号的波达方向，估计结果也较为准确。

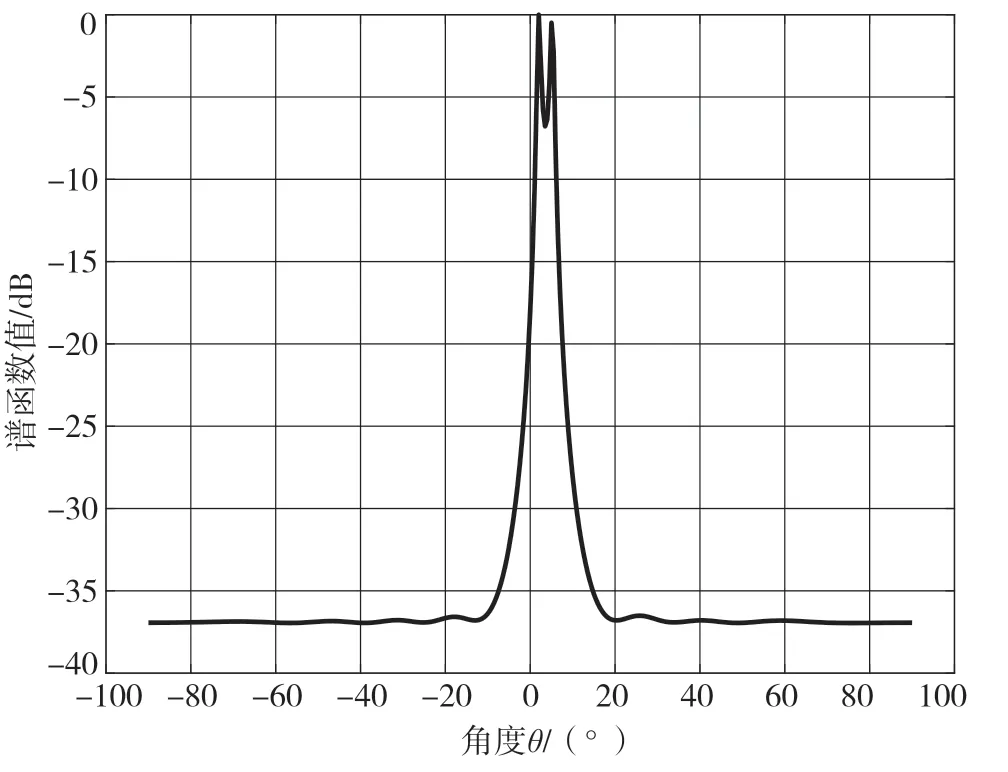
图5 改进型MUSIC 算法的谱函数图像

实验结果表明，提出的改进型MUSIC 算法在小信噪比和小快拍数的条件下，性能明显优于传统的MUSIC 算法。新算法具有更广泛的应用场景。

4.3 实验3：两种算法随信噪比和快拍数变化的分辨率对比

本实验假设采用阵元数为10、阵元间距为入射信号波长的一半的均匀线阵，噪声为高斯分布。随着每次仿真实验环境变化，计算出的校正值α也有差别。大量仿真结果表明，α值基本在1.0 处上下浮动。

图6 为在相同快拍数下，两种算法随信噪比变化而分辨力发生变化的分辨概率折线图。该实验中，设置固定快拍数为80，信噪比间隔为2 dB，从-6～6 dB均匀变化。对两种算法进行200次蒙特卡罗仿真试验。

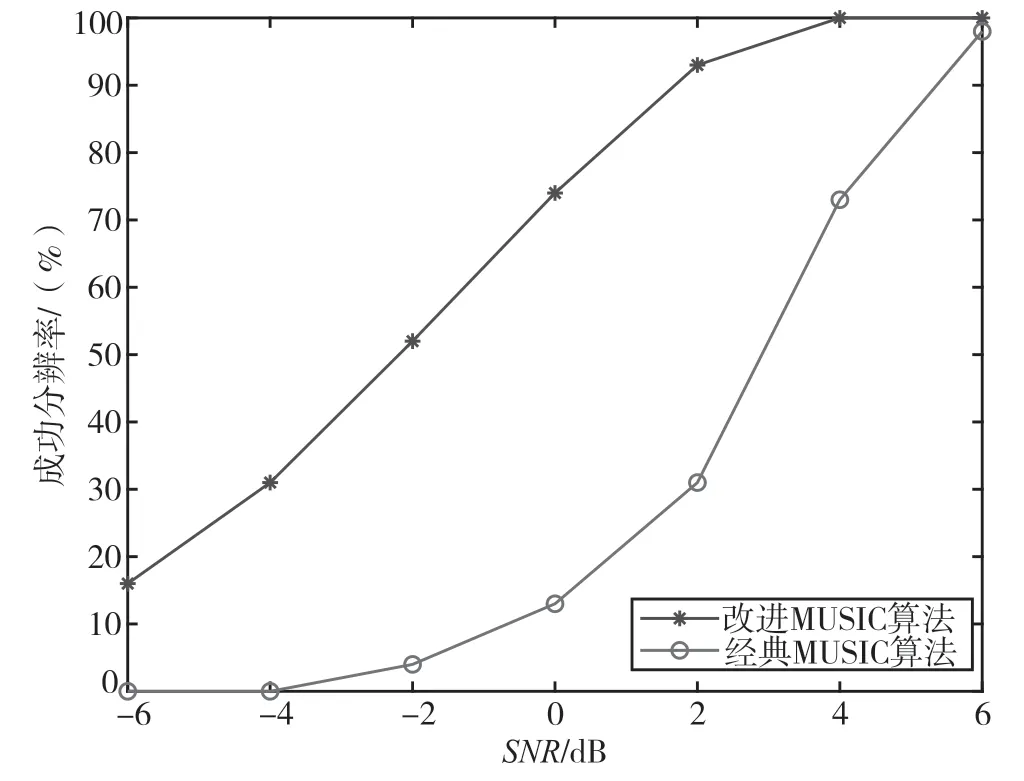
图6 两种算法在不同信噪比下的分辨率

图7 为相同信噪比、不同快拍数条件下，传统MUSIC 算法与改进型MUSIC 算法的成功分辨概率折线图。信噪比为8 dB。快拍数间隔为16，从16～112均匀变化，同样进行200次蒙特卡罗仿真试验。

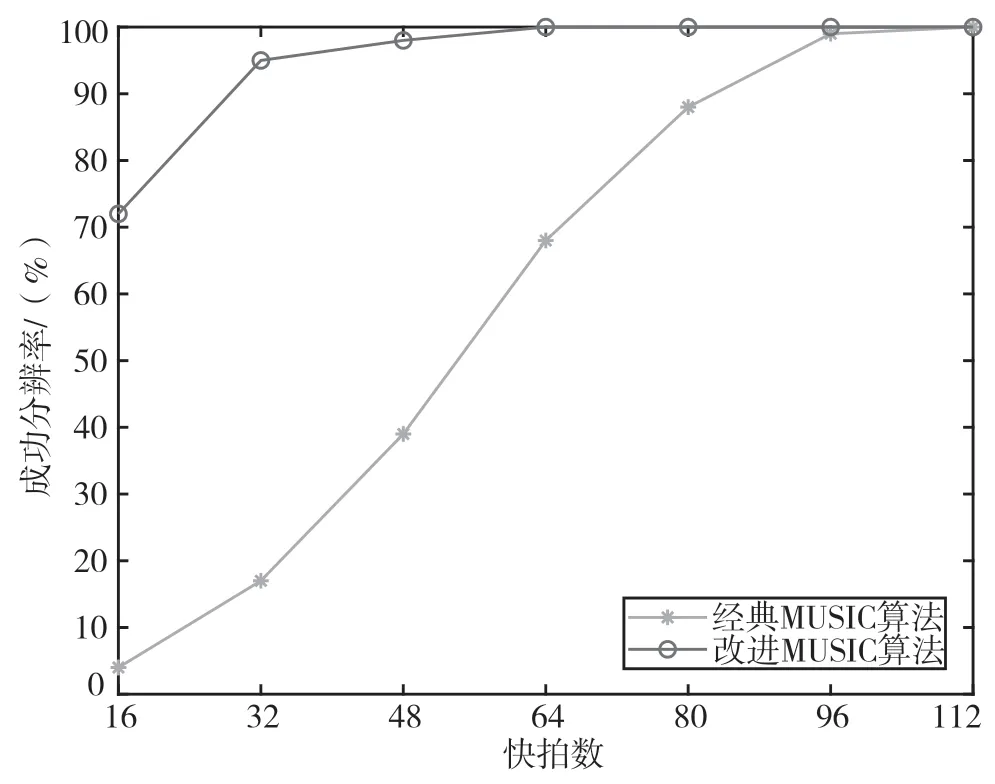
图7 两种算法在不同快拍数下的分辨率

从图6 能够看出，随着信噪比逐渐增加，传统MUSIC 算法和改进的MUSIC 算法成功分辨率也逐渐升高，但改进的MUSIC 算法成功分辨率明显高于传统的MUSIC 算法。从图7 中可以看出，随着快拍数的增加，两种算法分辨率逐渐升高，改进的MUSIC 算法同样明显优于传统的MUSIC 算法，进一步说明改进的MUSIC 算法有更好的分辨性能。

4.4 实验4：信号相干时传统MUSIC 算法与改进的空间平滑MUSIC 算法对比

本实验分别使用经典MUSIC 算法和改进的空间平滑MUSIC 算法进行实验仿真。假设信号源使用3 个波长为λ的相干窄带信号，分别从20°、40°和60°的方向入射到阵元数为10、阵元间距为λ/2 的均匀线阵上。信噪比为20 dB，快拍数为200，仿真结果如图8 所示。

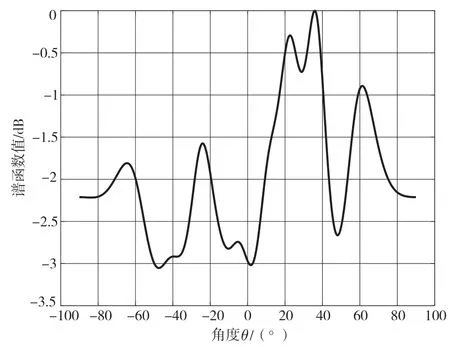
图8 传统MUSIC 算法的DOA 估计谱

在图8 中，传统MUSIC 算法无法对相干信号进行有效的DOA 估计。从图9 中可以看出，将前向后向平滑技术与改进MUSIC 算法相结合的新技术能够得到正确的谱峰，估计出的波达方向也十分准确。所以，新技术可以用于相干信号的波达方向估计。

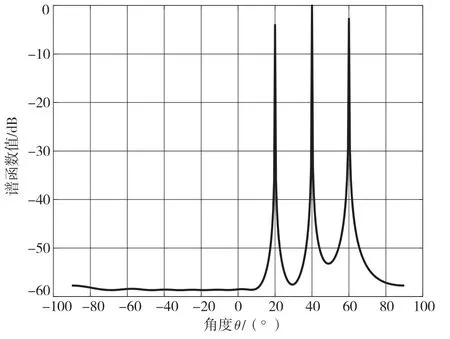
图9 改进算法的DOA 估计谱

5 结语

本文首先介绍了一种经典的DOA 估计技术，即MUSIC 算法。针对传统MUSIC 算法在低信噪比、小快拍数下分辨力低的缺陷，提出了一种基于噪声子空间投影的新型MUSIC 算法，然后进行仿真实验。在不同信噪比、不同快拍数条件下，测试传统MUSIC 算法和改进型MUSIC 算法的测向性能，并将两种算法的性能进行对比。实验结果表明，改进后的算法在低信噪比、小快拍数下依旧具有较高的分辨力以及较好的测向效果。新算法比传统MUSIC算法具有更广泛的应用场景。最后，针对传统MUSIC 算法对相干信号波达方向估计失效的缺陷，研究了经典的空间平滑算法原理，提出在使用改进MUSIC 算法进行波达方向估计前，先利用空间平滑算法处理相干信号，再对处理后的数据进行测向估计。论文同样对相干信号测向估计新技术进行了仿真实验，通过对比传统MUSIC 算法与新技术在处理相干信号时的算法性能，说明了将空间平滑技术与改进MUSIC 算法相结合的新技术能够很好地估计相干信号的波达方向。