小学生数学成绩与数学焦虑的关系：课堂注意行为当前的和纵向的作用

2021-06-22林子琪侯瑞豪高亚茹司继伟

心理研究 2021年3期

林子琪侯瑞豪刘芸高亚茹司继伟

（1东北师范大学心理学院，长春130024；2山东师范大学心理学院，济南250014）

1 引言

小学阶段是儿童大脑的内部构造和功能完善的关键阶段，儿童身心发生着显著的变化，这个时期对于培养儿童的感知能力、注意习惯和学习能力非常重要（马超，2013），所以选取小学生作为被试来研究课堂注意行为、数学焦虑与数学成绩的联系，既符合现状又具有现实意义。

个人在了解数学并参加与数学有关的活动时产生的一系列身心上的消极情绪反应就是数学焦虑（陈英和，耿柳娜，2002）。甚至在儿童时期，数学焦虑就已经被发现是一个独特的概念，不同于考试焦虑和一般焦虑（Carey，Hill，Devine，＆Szücs，2017）。

课堂注意行为指学生在参与课堂活动或学习的时候表现出来的注意行为。积极的注意行为，即课上集中注意力，完成老师所要求的任务，可以促进学生对知识的理解和学习；消极的注意行为，即课上分心，进行其他不适宜的、影响课堂学习的行为，会干扰学生的学习效果（周玲玲，2012）。

1.1 数学成绩与数学焦虑

数学焦虑研究最稳定的结果是其与数学成绩之间的关系。许多研究者都在对数学焦虑和数学成绩之间的关系进行探讨，主要的观点分为三种。第一种是数学焦虑会对数学成绩产生不良影响。Carey等人（2016）提出衰弱焦虑模型（d ebilitating a nxiety m odel），认为高数学焦虑会导致低数学成绩。

第二种是低能力解释（r educed c ompetency a ccount），认为数学焦虑实际上是低数学能力的结果，学生较低的数学能力导致不合理的表现和学习行为，造成数学焦虑。Maloney（2016）研究发现，低能力者会增加对数学中负面社会线索的敏感性从而产生焦虑情绪。Hembree（1990）也发现低数学能力学生会避免参加数学课程，并较少利用机会（如做数学作业，参与数学课）磨炼他们的数学能力。这种回避使学生的数学理解更加落后，并产生数学焦虑。与该主张一致，有数学焦虑的学生报告较少参加数学课（Ashcraft＆Kirk，2001；Hembree，1988），并且通常来说，青少年学生的数学焦虑与较少学习数学课程的意图相关（Eccles，1984； Eccles，Adler，＆Meece，1984）。

第三个模型是交互理论（r eciprocal t heory），数学焦虑和成就相互影响，形成恶性循环（Carey et al.，2016）。Gunderson等人（2018）发现，一、二年级学生的数学焦虑与学生成绩之间存在交叉滞后关系。虽然这些关系是相互的，但最初的成绩对后来焦虑的影响要强于焦虑对以后成绩的预测作用。

1.2 数学成绩与课堂注意行为

课堂注意行为一直被认为是整个人生发展过程中学业成绩不良的风险因素（Garner et al.，2014）。丁锦宏等人（2012）对9～13岁的学生进行了研究，结果显示，成绩优秀的学生注意能力更高，而成绩较差的学生注意能力更低。张曼华等（1999）使用相关分析对82名小学生的注意品质与学习成绩的关系进行研究，发现注意广度、注意分配以及注意稳定性与学习成绩都有明显的正相关，其中注意稳定性的分心程度与数学成绩呈显著负相关。国外的研究者也发现相较于智力，课堂注意行为与数学成就测验成绩的相关程度更高（Duncan et al.，2007）；相较于智力和工作记忆，课堂注意行为与纸笔测验中算术成绩的相关程度更高（Fuchs et al.，2006；Fuchs et al.，2010）。由此推断，数学成绩和课堂注意行为之间存在正向关系。

1.3 课堂注意行为与数学焦虑

注意控制是个体积极或消极地控制自己反应的一种能力，包括注意集中、注意转移和控制想法三个次级因素（杨慧芳，党晓姣，黄珊珊，窦伟伟，董梦晨，郑希付，2013）。根据注意控制理论，高焦虑会损害一个人抑制任务无关信息处理和在不同任务之间转换注意力的能力。在一个8至12岁儿童的非临床样本中，控制年龄和性别后，发现高度焦虑与自我报告的注意力控制呈负相关（Muris et al.，2008）。Rueda等人（2005）通过研究发现，不良的注意力控制可能通过抑制与任务无关的信息处理，削弱对压力的认知和情绪反应，从而导致焦虑。Rachel等人（2017）采用注意范式进行研究，结果表明，在注意范式的行为结果上，数学焦虑与注意力对数学符号的脱离有关。由此推测，数学焦虑和注意之间存在负向关系。

综上所述，目前大部分研究探讨数学焦虑对数学成绩的影响，而较少研究数学成绩对数学焦虑的影响。Ma和Xu（2004）等人曾在此方面进行过研究，但研究的群体为初中生和高中生，且研究的是数学成绩和数学焦虑间的因果关系，未探讨其他因素的作用。现以三、四年级学生作为被试，探讨数学成绩、课堂注意行为和数学焦虑三者间的关系。此外，关于课堂注意行为、数学焦虑和数学成绩之间联系的纵向研究多是在西方背景下进行的（Geary，2012），国内对该方面的研究多局限于横断研究（李梦霞，2017；陈琪，2016），难以揭示课堂注意行为、数学焦虑、数学成绩三者的联系随时间的变化趋势与作用机制。因此，拟通过中介效应分析来更好地探究小学儿童的课堂注意行为、数学焦虑与数学成绩当前和纵向的联系，提出两个假设：（1）数学成绩和数学焦虑存在显著的负相关；（2）课堂注意行为在数学成绩和数学焦虑间起中介作用。

2 方法

2.1 被试

采用整班抽样，选取山东省某小学三、四年级232名学生为研究对象，以班级为单位，获得知情同意后采用统一指导语进行两次集体施测，时间间隔为一年，时间点分别为（T1、T2）。两次施测完毕后，删除只参加其中一次的被试以及无效问卷（多处不选或多处重复选），共得到有效被试190人，有效数据380份。其中，男生98人，女生92人，年龄分布在8～13岁之间，平均年龄10.17岁，三年级80人（42.1%），四年级110人（57.9%）。

2.2 研究工具

2.2.1 儿童数学焦虑量表

采用耿柳娜和陈英和（2005）修订的儿童数学焦虑量表（MASC），该量表用来测查儿童的焦虑水平。修订后的量表包含22道题目，可以归纳为四个维度：数学评估焦虑、数学学习焦虑、数学问题解决焦虑和数学教师焦虑。量表采用4级评分，1～4焦虑程度递增，1表示完全不焦虑，4表示极度焦虑，量表最后得分是所有题目得分之和。本研究中量表的α系数为0.90，说明信度良好。

2.2.2 注意缺陷多动障碍评定量表——注意分量表

译自Swanson等人（2001）编制的The SNAPIV Rating Scale，该量表包含18个题目，分为“注意”和“多动”两个分量表。量表采用4点计分，0表示完全没有，1表示偶尔有，2表示总是这样，3表示非常多，量表上的得分越高，反映受试者该方面的注意水平越低。本研究使用全量表进行测试，但分析数据时只使用“注意”分量表。其中项目多为课堂中典型儿童的行为，对课堂环境的要求更为敏感（Gray，2015）。注意分量表Cronbachα系数为0.82，说明量表信度较好，KMO值为0.81，说明量表的效度较高，Bartlett检验结果p值＜0.05，该次问卷有效。

SNAP—IV量表虽是一个临床量表，但也曾用于测量正常儿童。温鸿洋（2019）在改善小学低年级学生注意力不集中的实验中采用SNAP—IV量表和ADHD评定量表测量学生的注意力、多动等，认为使用这两个量表并不是要诊断学生的多动行为，只是参考ADHD的测评标准来数据化评量学生的多动行为。同样，虽然SNAP—IV量表是一个临床量表，但因为此量表在注意领域内得到广泛应用，所以现采用该量表对学生的注意行为进行数据化评量。此外，受当时条件限制，量表无法交由教师或家长完成，考虑到学生处于三、四年级以及问卷内容并无晦涩难懂之处，加之现场收发量表并进行讲解，所以交由学生自己完成，对完成后的问卷进行了信效度检测，结果均良好。

2.2.3 数学成绩

数学成绩指标采用学生在两次期末考试中的数学成绩，为便于不同班级间的比较，将成绩进行班级内标准化。

2.3 研究程序

应用心理学本科生为主试，以班级为单位，采用集体施测的方式。主试根据统一的指导语，对被试讲明调查内容和注意事项，向被试说明调查结果不会计入成绩，然后被试填写问卷，完成后当场回收。施测两次，时间间隔为一年，每次均做儿童数学焦虑量表、注意缺陷多动障碍SNAP—lV评定量表。

2.4 统计分析

对收集的数据整理录入、相关分析、中介分析等均采用SPSS 19.0软件。

3 结果和分析

3.1 共同方法偏差检验

由于本研究测量数学焦虑和课堂注意行为的量表均为自我报告，可能存在共同方法偏差问题（周浩，龙立荣，2004），因此在研究设计上采用正反向计分和隐私保护承诺控制，并采用Harman单因素检验对可能存在的共同方法偏差进行检验。结果发现，第一公因子解释率为29.01%，小于40%的临界标准，说明本研究不存在严重的共同方法偏差。

3.2 小学生课堂注意行为、数学焦虑与数学成绩的描述统计和相关分析

采用Pearson积差相关分析考察T1、T2小学生课堂注意行为、数学焦虑与数学成绩的关系，结果发现（详见表1）：课堂注意行为（r＝0.46，p＜0.01）、数学成绩（r＝0.61，p＜0.01）在两时间点具有高度的正相关，数学焦虑各维度显著正相关（rs＞0.16，ps＜0.05），表明小学生课堂注意行为、数学焦虑与数学成绩在半年内表现出一定的稳定性。

表1显示同一时间点的数学焦虑和课堂注意行为之间呈显著正相关。此外，无论是在T1还是T2，课堂注意行为与数学成绩、数学焦虑与数学成绩的同时性和继时性相关均显著。

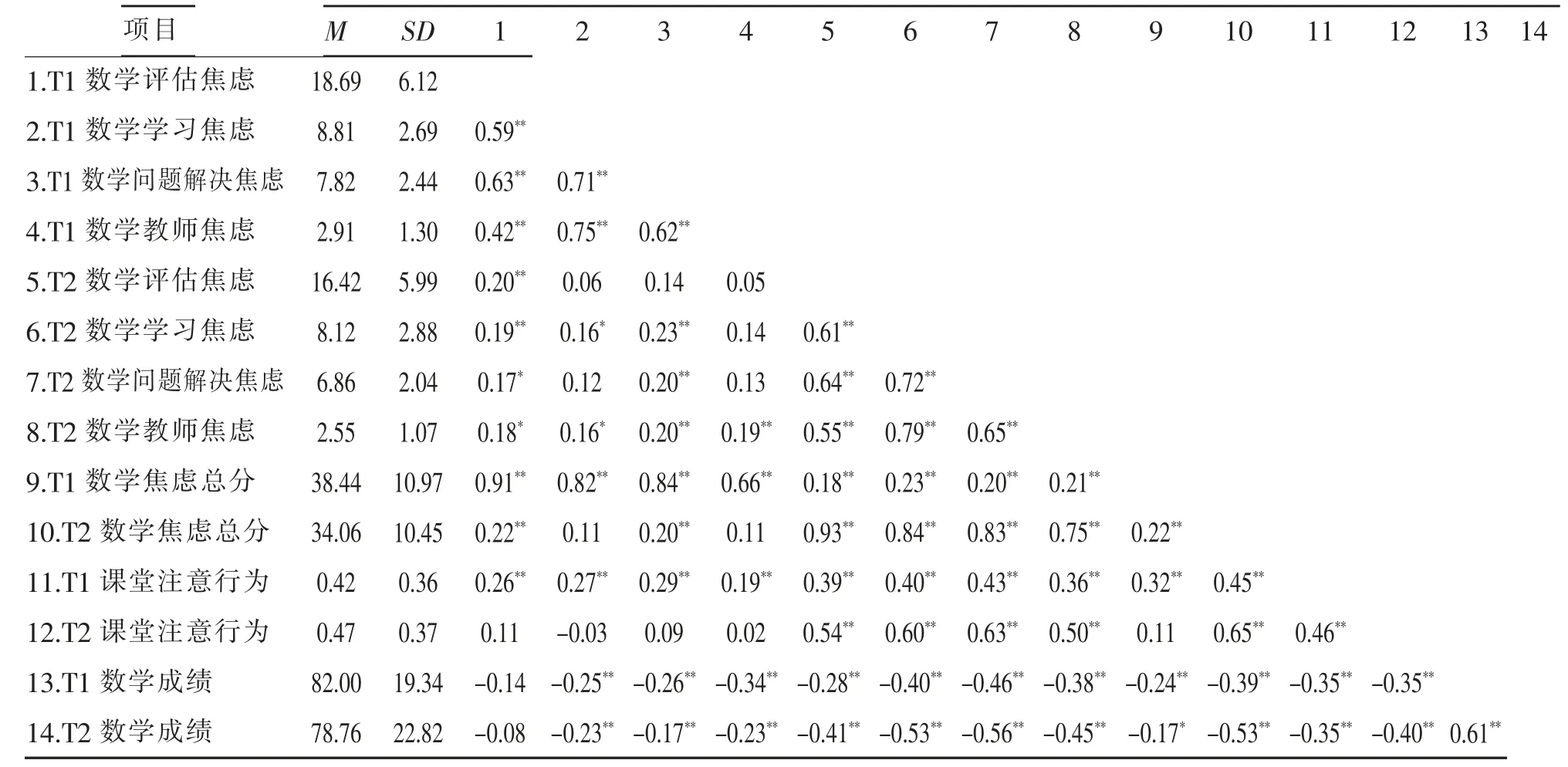
表1 小学生课堂注意行为、数学焦虑与数学成绩的描述统计和相关分析

3.3 小学生课堂注意行为、数学焦虑与数学成绩之间的中介效应检验

3.3.1 当前小学生课堂注意行为、数学焦虑与数学成绩之间的中介效应检验

使用T1收集的数据，采用SPSS软件中的PROCESS插件中的模型4，参照温忠麟和叶宝娟（2014）提出的检验程序来进行中介效应检验。自变量是数学成绩，中介变量是课堂注意行为，因变量是数学焦虑，并将性别和年龄作为控制变量，构造中介模型，用Bootstrap法进一步验证中介模型是否成立。将重复取样设定为1000，中介效应量的置信区间为95%，如果a，b系数的95%置信区间没有包括0，则表明中介效应显著。

数学成绩对数学焦虑的回归系数c为－2.64（t＝－3.38，p＝0.001），达到显著水平；数学成绩对课堂注意行为的回归系数a为－0.12（t＝－4.97，p＜0.001），95%置信区间不包含0，为［－0.17，－0.07］；课堂注意行为对数学焦虑的回归系数b为9.17（t＝4.04，p＜0.001），95%置信区间不包含0，为［4.69，13.66］，达到显著水平；数学成绩和课堂注意行为对数学焦虑的回归系数c’为－1.54（t＝1.93，p＝0.06），不具有显著性，说明课堂注意行为完全中介了数学成绩和数学焦虑的关系（如图1所示），其中ab／c＝0.42，即中介效应占总效应的比例为42%，该中介模型成立。

图1 当前小学生课堂注意行为、数学焦虑与数学成绩之间的中介效应检验

3.3.2 纵向小学生课堂注意行为、数学焦虑与数学成绩之间的中介效应检验

使用T1和T2收集的数据，采用SPSS软件中的PROCESS插件中的模型4，参照温忠麟和叶宝娟（2014）提出的检验程序来进行中介效应检验。自变量是T1数学成绩，中介变量是T2课堂注意行为，因变量是T2数学焦虑，性别和年龄作为控制变量，构造中介模型，用Bootstrap法进一步验证中介模型是否成立。将重复取样设定为1000，中介效应量的置信区间为95%，如果a，b系数的95%置信区间没有包括0，则表明中介效应显著。

T1数学成绩对T2数学焦虑的回归系数c为－4.08（t＝－5.81，p＜0.001），达到显著水平；T1数学成绩对T2课堂注意行为的回归系数a为－0.13（t＝－5.03，p＜0.001），95%置信区间不包含0，为［－0.18，－0.08］；T2课堂注意行为对T2数学焦虑的回归系数b为17.09（t＝10.51，p＜0.001），95%置信区间不包含0，为［13.89，20.30］，达到显著水平；T1数学成绩和T2课堂注意行为对T2数学焦虑的回归系数c’为－1.92，（t＝－3.23，p＜0.05），具有显著性，说明直接效应显著。ab与c’的符号相同，均为负号，说明T2课堂注意行为在T1数学成绩和T2数学焦虑间起部分中介作用（如图2所示），其中ab／c＝0.54，即中介效应占总效应的比例为54%，该中介模型成立。

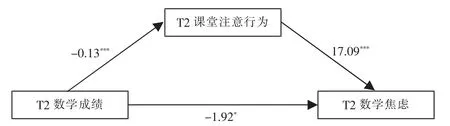
图2 纵向小学生课堂注意行为、数学焦虑与数学成绩之间的中介效应检验

4 讨论

4.1 小学生数学成绩和数学焦虑的关系

本研究的结果支持低能力解释的观点，即数学成绩差会导致数学焦虑（Carey et al.，2016）。无论是横向还是纵向的情况下，小学生数学成绩都可以负向预测数学焦虑。以往也有一些研究结果与之相符，Ma和Xu（2004）在一项对初中生和高中生的研究中得出结论，先前的低数学成绩预示着以后的高数学焦虑，但先前的高数学焦虑并不能预测以后的低数学成绩。此外，研究表明，患有数学学习障碍的小学儿童的数学能力较差，他们报告的焦虑程度高于同龄人（Passolunghi，2011；Wu et al.，2014）。

确实较少有研究在小学生群体中直接测试低水平的数学成绩是否预示着更高水平的数学焦虑，但可以从与数学焦虑有关的研究（例如任务回避行为和数学兴趣）以及与数学成绩有关的研究（例如感知的数学能力）中获得提示。在一年级学生中，数学能力较低的学生在学校中随着时间的推移会有更多的任务回避行为，并且任务回避行为是高度数学焦虑的标志（Onatsu－Arvilommi＆Nurmi，2000）。在幼儿园，最初兴趣高的学生随着时间的推移表现得更好，而那些最初表现好的学生随着时间的推移表现出更多的兴趣，这是一种相互关系（Fisher，Dobbs－Oates，Doctoroff，＆Arnold，2012）。在一项对7到9年级学生的研究中发现，数学能力越高的学生，随着时间的推移，数学焦虑越低（Meece，Wigfield，＆Eccle，1990）。

4.2 课堂注意行为在小学生数学成绩和数学焦虑间的中介作用

在横向研究中，课堂注意行为在数学成绩和数学焦虑间起完全中介作用，即数学成绩会通过课堂注意行为影响数学焦虑；在纵向研究中，T2课堂注意行为在T1数学成绩和T2数学焦虑间起部分中介作用，表明T1数学成绩不仅直接影响T2数学焦虑，还可以通过T2课堂注意行为影响T2数学焦虑。

在纵向研究中，小学生数学成绩除了通过课堂注意行为对数学焦虑起作用外，还可以直接影响数学焦虑。这很可能是因为纵向研究给与了这种关系时间来发挥作用，因为横截面模型经常是有缺陷的，这些模型不能考虑时间滞后的问题（Gollob，Reichardt，1987）。Ma等人（2004）进行了一项长达6年的纵向研究，认为数学焦虑和数学成绩之间的交叉滞后单向路径规定了前一年数学成绩对下一年数学焦虑变化的因果贡献，其中的交叉滞后效应表明先前的数学成绩与后来的数学焦虑显著相关。同样，Riikka Sorvo等人（2019）通过为期一年的纵向研究发现，之前的算术成绩预测了后来对数学失败的焦虑。由此推测可能是纵向研究时间的延长使得小学生数学成绩对数学焦虑产生直接作用。