基于S型效用函数的农业旱灾脆弱性评估
——以河南省为例
2021-06-21郝慧慧朱涵钰李小鹏
郝慧慧,朱涵钰,李小鹏
(华北水利水电大学管理与经济学院,郑州 450046)
相对于洪水、地震、飓风等其他自然灾害,干旱灾害的孕育过程缓慢,容易被忽略,一旦形成灾害,会产生较大的影响.农业旱灾脆弱性是指农业生产系统易遭受干旱威胁并形成损失的性质[1],与农业生产有着紧密联系.农业旱灾脆弱性具有相对性和可变性的特点,运用当前的技术手段很难准确预测农业旱灾.降低农业旱灾脆弱性成为旱灾风险管理的一个核心要素,为减轻农业旱灾造成的损失,研究农业旱灾脆弱性评价就显得尤为重要.
对农业旱灾脆弱性评估,不同地区有不同的评价标准.河南省是农业旱灾发生以及造成经济损失可能性最高的省份,目前省内还没有农业旱灾脆弱性的一个统一的衡量标准.近年来,国内外学者对于农业旱灾脆弱性的研究不断丰富和完善.主要概括为两个部分:在评估方法方面,王莺等[2]运用主成分分析方法建立了中国南方地区的旱灾脆弱性模型;SUN[3]基于面板数据提取了旱灾脆弱性的关键影响因子;KIM等[4]采用主成分分析方法分析了韩国县市机关对农业旱灾脆弱性的反应;许朗等[5]从敏感性和恢复力两个方面选取12个指标衡量河南和山东的农业旱灾脆弱性;代永强等[6]利用混合蛙跳算法投影寻踪模型对农业旱灾脆弱性进行综合评价;程静等[7]运用主成分分析方法和聚类分析,评估长江中下游六省一市的农业旱灾脆弱性;宋占智等[8]运用基于改进云相似度的方法建立了农业旱灾脆弱性评价模型评价了蚌埠市农业旱灾脆弱性.在指标体系构建方面,康永辉等[9]从自然因素、社会因素、经济因素3个方面构建了指标评价体系;王婷等[10]从水稻效率指数、应灾能力指数、水稻暴露指数3个方面构建了四川省水稻干旱脆弱性评价指标体系;马雅丽等[11]选取作物因素、环境因素和人为因素的11个指标对晋北地区农业旱灾脆弱性进行评估;BRANT[12]从农户视角分析认为农场农产品产量、非农户收入等影响农户旱灾脆弱性;SALAM等[13]认为,农户脆弱性与其对气候变化的适应能力相关.
农业旱灾脆弱性具有动态变化性、复杂性和不确定性等特征,其高低具有“放大”或“缩小”灾情的作用;正向指标变化较小时,旱灾脆弱性不明显;指标变化较大时,旱灾脆弱性出现指数趋势变化,随着指标的变化,脆弱性变化趋于平缓.负向指标对旱灾脆弱性的影响与正向指标具有对称趋势.可知脆弱性变化特征具有S型特性,因此本文引入S型效用函数.S型效用函数能够很好地刻画动态变化的行为,随着资源的增加,决策者敢于冒险,随着资源的积累,决策者逐渐停止冒险,归于平淡;相反,随着资源的逐渐减少,决策者的反映逐渐强烈,贫困积累到一定程度,会产生“破罐子破摔”的状况.因此,使用S型效用函数评估河南省农业旱灾脆弱性强度具有一定的合理性.
综上可以看出,对于农业旱灾脆弱性评价和指标选取方面,评价方法和分类标准多种多样.而农业旱灾脆弱性的抽象性和复杂性特点,使农业旱灾脆弱性评估面临两个挑战:第一个是农业旱灾脆弱性指标体系的构建,指标体系的构建基于主观因素,虽然可以证明指标体系的合理性,但是评价体系可能会出现指标重叠、冗余造成评价结果出现偏差;第二个是农业旱灾脆弱性指标权重确定的问题.以往研究多采用层次分析法和专家咨询法,具有较强的主观性,降低了指标的可信度,甚至造成评价结果出现错误.农业旱灾脆弱性是农业系统在内外扰动下的旱灾损失和防灾减灾能力的组合产物,因此,从自然、经济、社会3个方面选取指标对河南省农业旱灾脆弱性进行评估.目前尚未有研究借助于S型效用函数去评估农业旱灾脆弱性,本文针对农业旱灾脆弱性问题开展研究,首先进行研究区域的描述和数据的预处理,其次借助于粗糙集理论的属性约简进行指标的筛选,然后根据群体一致性和极大熵准则确定指标权重,最后运用S型效用函数求解农业旱灾脆弱性,并借助于ArcGIS自然断点法进行空间区划,构建河南省农业旱灾脆弱性评估模型,为河南省农业旱灾脆弱性评估决策以及防灾减灾提供科学的建议.
1 研究区概况与数据来源
1.1 研究区概况
河南省位于我国中东部,地理位置北纬31°23′~36°22′,东经110°21′~116°39′,东接安徽、山东,南邻河北、山西,北靠湖北,土地面积为16.7万km2,有17个省直辖市和1个省直管市,20个县级市,83个县,53个市辖区.河南省地处亚热带和暖温带气候区,地形,地貌,土壤,气候都有明显的过渡性特征,地势西高东低,中东部为平原,西南部为丘陵.复杂的地势地貌形成了特殊的孕灾环境,因此河南省自然灾害频发,其中旱灾成为影响河南省最严重的农业自然灾害.
1.2 数据来源和预处理

2 农业旱灾脆弱性评价指标体系的构建
2.1 指标选择与处理
包括社会、经济、人口、教育、基础设施等许多因素造成了农业旱灾脆弱性.大量的农业旱灾脆弱性指标在农业旱灾脆弱性评估中具有一定的说服力,但随机选取农业旱灾脆弱性指标不能科学的反映农业旱灾脆弱性信息.把农业旱灾脆弱性(A)分为3个方面:自然脆弱性(B1)、经济脆弱性(B2)和社会脆弱性(B3).自然脆弱性主要包括降雨量(C1)、年平均气温(C2)、造林面积(C3)、旱地面积(C4);经济脆弱性主要包括人均GDP(C5)、农村居民可支配收入(C6)、财政支农资金(2017年)(C7)、第一产业值(C8);社会脆弱性主要包括R&D人口数(C9)、农业就业人口数(C10)、播种面积(C11)、国际互联网用户(C12)、水库数量(C13)、机电总眼数(C14).在前人研究文献的基础上,从自然脆弱性、经济脆弱性和社会脆弱性3个方面选择了14个指标.
农业旱灾脆弱性指标分为正指标和负指标,因为它们同时具有正的和负的贡献.正向指标表明,可变值的增加对应于农业旱灾脆弱性的增加;负向指标表明,可变值的增加对应于农业旱灾脆弱性的减小.与农业旱灾脆弱性呈正相关的脆弱性指标有C4,C8,C10和C11,表明农业旱灾脆弱性较高;C1,C2,C3,C5,C6,C7,C9,C12,C13和C14等指标与农业旱灾脆弱性呈负相关,表明农业旱灾脆弱性较低,通过区间标准化公式计算(数据来源于2019年《河南省统计年鉴》),得到河南省农业旱灾脆弱性指标的标准化数据(表1).

表1 河南省农业旱灾脆弱性标准化数据Tab.1 Standardized data on agricultural drought vulnerability in Henan Province
2.2 基于粗糙集理论的属性约简
在农业旱灾脆弱性评价中,如果研究者在盲目追求完备性的情况下选择尽可能多的指标,可能会干扰主要因素的识别[14].针对农业旱灾脆弱性评价指标体系中指标信息的重叠,采用粗糙集理论对指标体系进行优化.1982年,波兰学者Pawlak提出了粗糙集理论,作为描述不完全性和不确定性的数学工具[15].粗糙集理论不仅可以有效地分析不确定性、不一致性和不完全信息,而且可以通过数据分析使指标体系合理化.属性约简是指知识库在保持相同情况下的分类能力,删除不相关或不重要的知识不会影响原有的知识体系,达到优化指标体系的目的.
粗糙集理论只能处理离散数据,因此在属性约简前对数据进行离散化.根据每个属性的特点,本文采用K-means聚类对各指标进行分析,得到数据离散化结果(表2).

表2 数据离散化结果Tab.2 Data discretization results
应用粗糙集理论对3个层次的指标进行属性约简.根据粗糙集属性约简的特点,相应的计算过程如下:社会脆弱性指标S=(U,A).
其中U={1,2,…,18},1~18代表河南省18个地市,A={C9,C10,C11,C12,C13,C14}.
U/ind(A)={{1},{2},{3},{4},{5},{6,8,11,12,18},{7},{9,10},{13},{14},{15},{16,17}},
U/ind(A-{C9})={{1,6,8,11,12,18},{2},{3},{4},{5},{7},{9,10},{13},{14},{15},{16,17}},
U/ind(A-{C10})={{1},{2},{3},{4,6,8,11,12,18},{5},{7},{9,10},{13},{14},{15},{16,17}},
U/ind(A-{C11})={{1},{2},{3},{4},{5},{6,8,11,12,18},{7},{9,10},{13},{14},{15},{16,17}},
U/ind(A-{C12})={{1},{2},{3},{4},{5,7},{6,8,11,12,18},{9,10},{13},{14},{15},{16,17}},
U/ind(A-{C13})={{1},{2},{3},{4},{5},{6,8,11,12,18},{7},{9,10},{13},{14},{15},{16,17}},
U/ind(A-{C14})={{1},{2,5},{3},{4},{6,8,9,10,11,12,18},{7},{13},{14},{15},{16,17}}.
可以看出:
U/ind(A)=U/ind(A-{C11})=U/ind(A-{C13})≠U/ind(A-{C9})≠
U/ind(A-{C10})≠U/ind(A-{C12})≠U/ind(A-{C14}).
删除指标C11和C13,得到新的评价指标体系为自然脆弱性包括降雨量(C1)、年平均气温(C2)、造林面积(C3)、旱地面积(C4),经济脆弱性主要包括人均GDP(C5)、农村居民可支配收入(C6)、财政支农资金(2017年)(C7)、第一产业值(C8),社会脆弱性主要包括R&D人口数(C9)、农业就业人口数(C10)、国际互联网用户(C12)、机电总眼数(C14).
2.3 求解权重

由两个值的偏差求得指标一致性优化目标M1:



由指标的一致性原理和极大熵准则得到最优化模型M[16]:


3 方法描述
S型效应函数是指在不同的财富水平上,效用函数展现不同的图像形式.如在某一财富水平之上,效用函数表现为凹函数;在某一财富之下,效用函数表现为凸函数,因其整体图像形似英文字母S,故称作S型效应函数.在金融学中用S型效用函数去刻画决策者的主观风险态度[17],能够很好地刻画决策者的行为特征,认为决策者在财富较多时为风险规避者,在财富较少时为风险偏好者[18].农业旱灾脆弱性趋势符合效用函数的特征,当效用值较低时,脆弱性较小,随着效用值的不断增加,脆弱性强度增加,但增加趋势逐渐缓慢平稳.前景理论[19]中的价值函数即为典型的S型效用函数,前景价值函数定义如下:

式中:v(x)为价值函数;b表示参考点,当x高于参考点时,视为相对收益;当x低于参考点时,则视为相对损失;α和β为风险态度系数,且0<α,β<0;θ为损失规避系数,决策者对损失的敏感程度随θ的增大而增大.
作为前景理论的基本假设之一,前景价值函数中的S型效用函数为幂效用函数形式,可视为S型效用函数的一个特例.由于双曲绝对风险规避函数可以通过选取不同参数值来包含多种效用函数形式,故将其引入到S型效用函数中,结合式(4),得到S型效用函数的一般情形如下:

式中:Δx=x-b,当x>b时,Δx>0,表示相对收益,当x<b时,Δx<0,表示相对损失;θ>1为损失规避系数;φ1,φ2,η1,η2>0;γ1,γ2∈(-∞,0)⋃(0,1).选取参数φ1=φ2=5,η1=η2=2,γ1=γ2=0.3,θ=1.5[20],b为各属性的均值,评估农业旱灾脆弱性.

式中:DV为综合效用值即农业旱灾脆弱性;U(i)为各指标效用值;ωi为权重.
4 结果讨论与政策建议
由上述计算得到农业旱灾脆弱性的结果(表3).
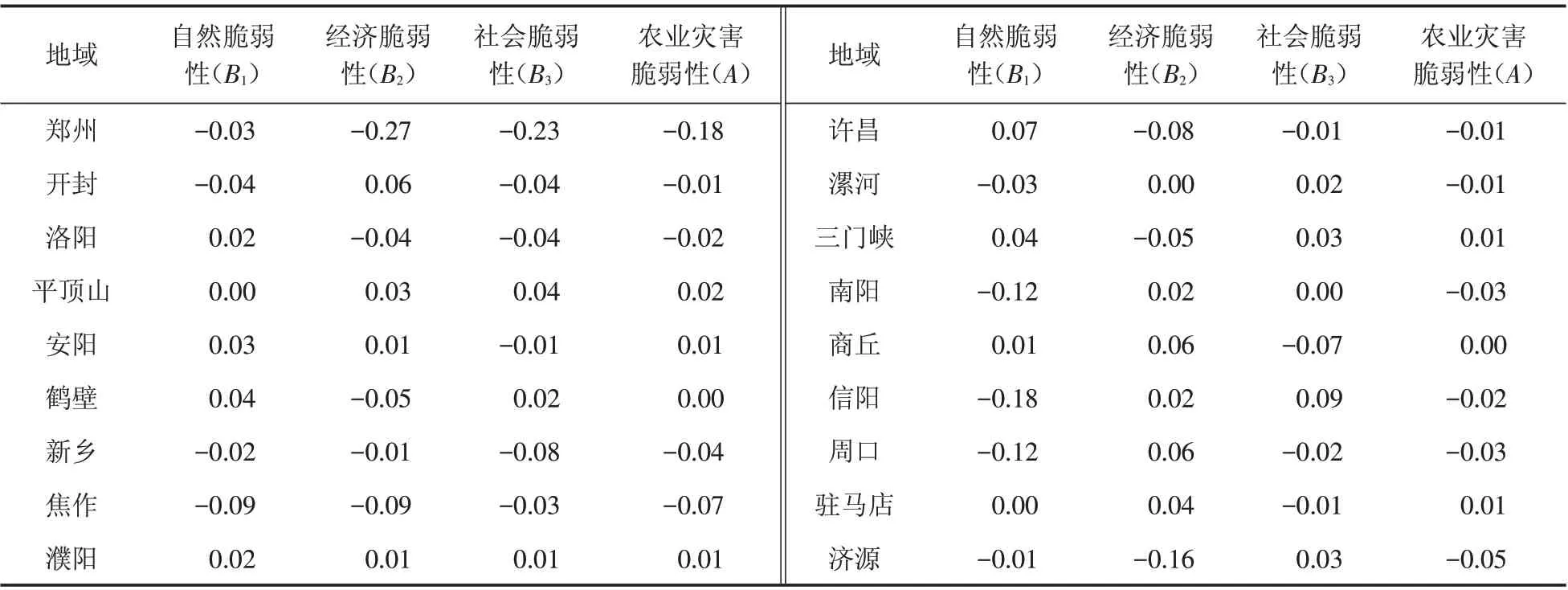
表3 农业旱灾脆弱性总体结果Tab.3 Overall results of agricultural drought vulnerability
由表3可知,河南省农业旱灾脆弱性具有明显的差异,中东部地区地势平坦,有效灌溉面积较大,农业投入较多,经济水平较发达,降水相对比较丰富,旱灾脆弱性较低,但仍存在旱灾发生的风险,需加强水利调配和灌溉优势;西南部地区多丘陵,降水量较少,水系不发达,农田水利基础设施薄弱,农业支出占财政支出比例较低,教育水平投入较少,有效灌溉面积小,抗旱意识薄弱,农业旱灾脆弱性很高,应调整农作物种植结构,大力推广防旱减灾种植技术,增强对天然水分的收集存储能力,提高水分的利用效率,降低农业旱灾脆弱性.
根据各指标的计算结果和等级划分原则,借助于ArcGIS软件,使用自然断点法进行分级,将农业旱灾脆弱性分为5个等级,绘制出河南省农业旱灾自然脆弱性、经济脆弱性、社会脆弱性和整体脆弱性分区图(图1).
由图1 a可知,自然脆弱性较强的地区为三门峡、安阳、鹤壁、许昌,自然脆弱性较弱的地区为焦作、信阳,其他地区自然脆弱性处于中等水平.三门峡位于河南省西部丘陵地带,农业对于自然依赖性较大,即该地区的自然脆弱性较强.
由图1 b可知,经济脆弱性较强的地区为开封、商丘、周口、驻马店,经济脆弱性较弱的地区为济源、郑州、信阳,其他地区处于中等水平.就经济发展水平来说,郑州是省会城市,人均GDP高于其他地区,财政支出在农业占比较重,经济发展速度较快,抵御旱灾的能力较强,因此郑州的经济脆弱性较低.近年来,开封的经济水平不断下滑,农村居民可支配收入降低,在一定程度上形成开封的经济脆弱性不断增加的趋势.
由图1 c可知,社会脆弱性较强的地区为信阳、濮阳、三门峡、济源,社会脆弱性较弱的地区为郑州,其他地区处于社会脆弱性中等水平,由信阳、濮阳、三门峡位于丘陵地带,人口密度较小,社会经济不发达,教育水平相对低于河南省的中东部地区,R&D人口数较低,基础设施不够完善,抵御旱灾的社会能力较弱.
由图1 d可知,农业旱灾脆弱性较强的地区为三门峡、平顶山、驻马店、安阳,农业旱灾脆弱性较弱的地区为郑州,其他地区处于农业脆弱性中等水平.由农业旱灾脆弱性影响因素可以看出,郑州独特的地理位置优势和财政倾斜力度,在一定程度上降低了农业旱灾脆弱性,而三门峡、平顶山等地区位于丘陵地带和河南省的边缘地区,经济水平相对落后,教育水平低于该省的中东部地区,财政支出较少,水利基础设施相对薄弱,这在一定程度上增加了农业旱灾脆弱性.
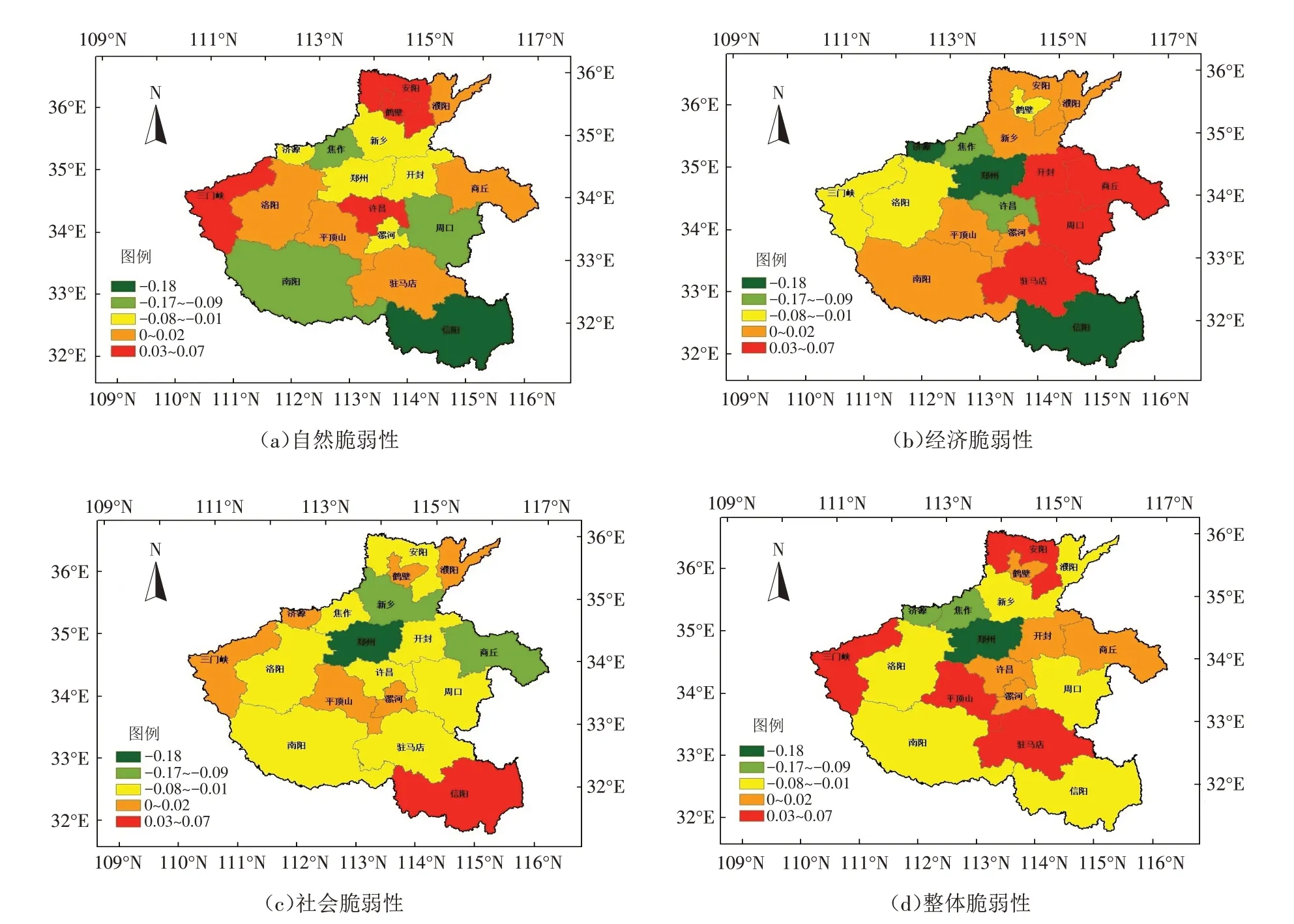
图1 河南省农业旱灾脆弱性分区图Fig.1 Regional map of agricultural drought vulnerability in Henan Province
根据河南省农业旱灾脆弱性分析结果,提出以下建议措施:
1)调整人口比例,控制人口结构.河南省不仅是农业大省还是人口大省,最突出的特点是城镇化水平低.大量的人口压力给农业造成了沉重的负担,面对旱灾发生时,抵御能力差,防御能力减弱.因此,调整人口比例,是河南省一项长期需要实施的对策.
2)增加水利基础设施建设,提高抗旱减灾能力.随着机电井眼数的增加,脆弱性降低,因此应注重灌溉措施的基础建设,完善基础配套工作,进行设备维修和更换,提高抗旱能力,从而降低农业脆弱性.
3)调整产业结构,降低农业依赖性.加快产业结构调整,增加第三产业就业人数,大力支持自主创业,提高政府投入资金,增加人口财富数量,降低农业依赖性,增强抗旱能力,从而降低农业旱灾脆弱性.
5 结论
以农业旱灾高发区的河南省为研究对象,从自然、社会、经济3个方面选取指标,建立农业旱灾脆弱性评估体系.在农业旱灾脆弱性指标的选取上,采用粗糙集理论属性约简的方法进行了指标优化,避免指标选取的冗余.在确定指标权重上,采用了极大熵原则和群体一致性准则求解属性权重,避免了主观评价对于结果的影响.最后运用S型效用函数进行农业旱灾脆弱性评估,使结果更加符合实际,并基于ArcGIS空间视图技术,应用自然断点法进行区划分析,得到河南省农业旱灾脆弱性区划图.整体来看,河南省农业旱灾脆弱性较高.从旱灾空间分布可以看出,中东部地区旱灾脆弱性较低,西南部旱灾脆弱性较高,与河南省地形分布具有一定的关系,同时也与社会和经济因素相关.建议西南部地区注重提高天然降水的收集和存储能力,增强基础设施建设,提高防旱能力.对于中东部脆弱性较低的区域,仍需提高旱灾防范意识,注重灌溉基础设施的安装和维护,加强水源调度和技术推广.
通过分析农业旱灾脆弱性的地理区划,在一定程度上提高了指标改进和结果优化,但对于指标的概括还存在不足,后期希望借助于大数据信息处理技术,继续进行指标的筛选、优化以及指标权重的确定.
