含间伐强度哑变量的关帝山油松天然林单木断面积生长模型构建

李学辉，白 宁，郭晋平，马建峰，张芸香

(1.山西农业大学林学院，山西 太谷 030801；2.关帝山国有林管理局，山西 文水 032100)

森林生长模型可以用来预估林分的生长和收获量，单木生长模型可以预测各单株林木的生长状况和生长潜力[1-4]，构建特定森林树种的单木生长模型对于区域森林经营具有重要意义[5]。在生长模型中用胸高断面积反映林木生长状况具有较高的准确性和稳定性，是构建林分和单木模型的合适指标[2，6]。根据竞争指标是否含有对象木与竞争木之间相对位置的信息，将单木模型分为距离有关单木模型和距离无关单木模型[7-9]。距离无关单木生长模型会导致相同大小林木若干年后仍为同样大小林木的结果，也无法反映林木在林分间伐前后竞争压力变化[10]。距离有关单木模型可以反映林木在林分中所处不同小生境的差异，并能较准确地反映竞争木间伐对主林木的影响[11]。

单木模型的建模方法包括潜在生长量修正法、回归估计法和生长分析法。潜在生长量修正法需要确定无竞争压力的疏开木，利用单木竞争指标对每株林木的潜在生长函数进行调整和修正，由于疏开木难以确定，因此该方法使用较少。回归估计法利用多元回归建立林木生长量与林木大小、林木竞争状态和所处立地条件等因子之间的回归方程，该方法建立的单木模型适应性差，预估能力依赖建模样本数据，且方程参数没有生物学意义。生长分析法以理论生长方程为基础模型，通过分析参数与单木竞争之间的关系构造单木模型，该方法不依赖疏开木的生长，选择合理的理论生长模型，可以获得良好的预测效果[12-14]。

在影响林木生长发育的因子中，不仅有许多定量因子，还有一些定性因子需要在建模中加以考虑，而构建含哑变量的模型可以有效表示定性因子[15-16]，因此，在单木模型中加入立地类型、林分类型、竞争类型等定性因子作为哑变量可以有效提高模型预测效果[17]。抚育间伐是基本的森林经营措施，显著影响林木胸径、断面积和材积生长，间伐强度是关键影响因素[18]。但将间伐强度作为哑变量加入到单木模型中的研究还鲜见报道。

油松(PinustabulaeformisCarr)为松科松属针叶常绿乔木，是我国特有树种，是黄土高原地区最主要的造林树种之一，油松天然林不仅在山西集中分布，在辽宁、河北、北京、内蒙古、陕西等地区也有广泛分布，在构建区域尺度景观多样性、保持水土和维持森林生态系统的稳定性等方面发挥着重要作用，具有较高的研究价值[19]。因此，通过选择合理的理论生长方程和参数，提高油松单木模型精度是当前在构建单木生长模型中亟待解决的问题。

本研究以山西关帝山林区油松天然林为研究对象，采用生长分析法的建模技术，将间伐强度作为哑变量引入模型，建立距离有关单木断面积生长模型，探究单木生长模型中加入间伐强度哑变量的建模途径和效果，构建含间伐强度哑变量的最优单木断面积生长模型，为油松天然林的经营管理提供科学依据。

1 研究区概况

研究区位于吕梁山中段关帝山林区(111°21′～111°37′E，37°45′～37°59′N)，是吕梁山断裂隆起的背斜构造山地，地形破碎，山体陡峻，沟壑纵横。林区气候受季风影响和控制，属于暖温带大陆性山地气候，夏季湿润多雨，冬季寒冷干燥，年均温4.2°C，年均降水量600～820 mm，年均相对湿度70.9%，年无霜期100～130 d，雪期和冻土期6个月，森林覆盖率71%。

孝文山林场位于关帝山林区中部，地处111°24′～112°37′E，37°41′～37°54′N，南北长约2 km，东西宽约17 km，海拔 1 345～2 659 m。主要森林类型建群树种有油松、华北落叶松(LarixprincipisvupprechtiiMayr)、青杄(PiceawilsoniiMast)、白杄(PiceameyeriRehd.et Wils)、白桦(BetulaplatyphyllaSuk)、辽东栎(QuercusliaotungensisMayr)等；主要林下灌木树种有三桠绣线菊(SpiraeatrilobataL)、黄刺玫(RosaxanthinaLinn.)、山刺玫(RosadavuricaPall.)、胡枝子(LespedezabicolorTurcz.)、水栒子(CotoneastermultiflorusBge.)等；主要林下草本植物有披针苔草(CarexlanceolataBoott)、蕨类(Pteridium)、地榆(SanguisorbaofficinalisLinn.)、金莲花(TrolliuschinensisBunge)等。

2 研究方法

2.1 样地设置与指标测定

于2019年7月对关帝山林区孝文山林场五十沟的9块固定样地进行复测，复测项目包括：号牌编码、胸径、单木位置和生长状况。经复测后根据林分内间伐(2013年)的林木断面积与林分总断面积之比，确定间伐强度，分为重度间伐、中度间伐、轻度间伐3类。并在每个样地内确定3株优势木，计算各样地优势木平均高。样地调查间隔期为5年。样地概况见表1。

表1 样地概况

2.2 对象木和竞争木确定

将样地内所有胸径≥5 cm的活立木作为对象木，靠近样地边界的对象木采用扩大缓冲区的办法确定竞争木[20]，缓冲区设在样地外围8 m范围内。9块样地的对象木共360株。

竞争木确定采用固定半径法[21]。为确定合理的竞争木测定范围，选取7株对象木，按竞争指数计算方法(公式1)，以1～12 m共计12个固定半径，分别计算其竞争指数，绘制固定半径与竞争指数增量的关系图(图1)，确定本研究竞争木的固定半径为6.4 m。

图1 不同半径的竞争指数增量Fig.1 Increment of competition index on different radius

2.3 样地调查取样和对象木胸高断面积测算

对样地内树高≥1.3 m的活立木进行每木编号和检尺，测定其胸径、树高(图帕斯TurPulse 200激光测距仪)和冠幅，并测定其相对位置，绘制林木定位图，用生长锥钻取对象木树芯，确定其年龄。由胸径计算出每株立木的胸高断面积。

2.4 竞争指数计算

从立木定位图测出对象木与各竞争木之间的距离，采用公式(2)(HEGYI公式)，计算出每株对象木的竞争指数：

(1)

式中：CI为某株对象木的竞争指数，Di为样地中第i株对象木的胸径，Dj为该对象木第j株竞争木的胸径，dij为该对象木i与其第j株竞争木之间的距离。

3 模型构建

3.1 基础模型构建

选用Logistic方程、Korf方程、Richards方程、Weibull方程，考虑立地质量、竞争指数、林木年龄3个因素。其中，立地质量用立地指数表达，本研究用样地优势木平均高代替地位指数。定义参数A是林木断面积的最大值[22]，受立地质量的影响；参数c与生长速度相关[23]，受竞争压力的影响。构造出4个单木断面积生长的基础模型表达式(表2)。

表2 基础模型表达式

3.2 间伐哑变量设置

将间伐强度作为哑变量引入单木断面积生长模型，用δ(x,i)表示[24]。其公式为：

(2)

3.3 模型参数求解和精度检验

运用R语言进行数据分析，采用最小二乘法求解模型参数。

为检验模型精度，以决定系数R2和预估精度P值选择模型，并对所选模型进行F检验，判断所选模型回归效果是否显著；选择总相对误差(TRE)、平均绝对误差(MAE)、均方根误差(RMSE)作为模型精度检验指标，比较基础模型和含哑变量模型的模拟效果。

(3)

(4)

P-1)

(5)

(6)

(7)

(8)

4 结果分析

4.1 基础模型拟合和精度检验

以关帝山360株油松为基础，利用基础模型表达式对树龄、优势木平均高及竞争指数进行拟合，结果见表3。

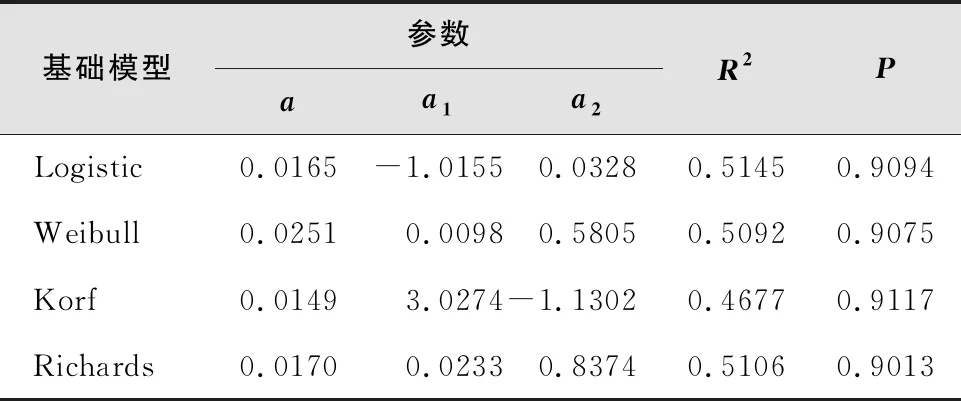
表3 基础模型参数与模型精度拟合

4种基础模型的R2为0.46～0.52，P值为0.89～0.92。各基础模型拟合度以Logistic模型最高，为 0.514 5；P值以Korf模型最高，为 0.911 7。

4.2 含间伐强度哑变量模型拟合与检验

将间伐强度分成3级，将间伐强度哑变量加入到模型的不同参数及其组合上，共构建了28种参数组合，利用360株对象木的生长数据进行参数估计，剔除不收敛参数组合，以参数显著性t检验和P值大小(以P≤0.05为标准)，剔除参数不符合的模型，再根据模型决定系数R2确定断面积生长模型的最优哑变量参数组合，进行模型选优。模型R2和P值见表4。

表4 含间伐强度哑变量模型精度拟合

含间伐强度哑变量的模型与基础模型相比P值和R2均有显著提高。含间伐强度哑变量的W模型R2总体来说大于其他含间伐强度哑变量模型，含间伐强度哑变量的K模型P值均大于其他含间伐强度哑变量模型。Logistic模型将间伐强度哑变量加到a、a2参数效果最优(L5)；Weibull模型将间伐强度哑变量加到a、a1、a2参数效果最优(W7)；Korf模型将间伐强度哑变量加到a1、a2参数效果最优(K6)；Richards模型将间伐强度哑变量加到a、a1、a2参数效果最优(R7)。

4.3 基础模型与含间伐强度哑变量模型的比较

为进一步确定基础模型与含间伐强度哑变量模型的精度差异，对基础模型和各含间伐强度哑变量最优模型的总相对误差(TRE)、平均绝对误差(MAE)及均方根误差(RMSE)3个精度检验指标进行对比分析(表5)。

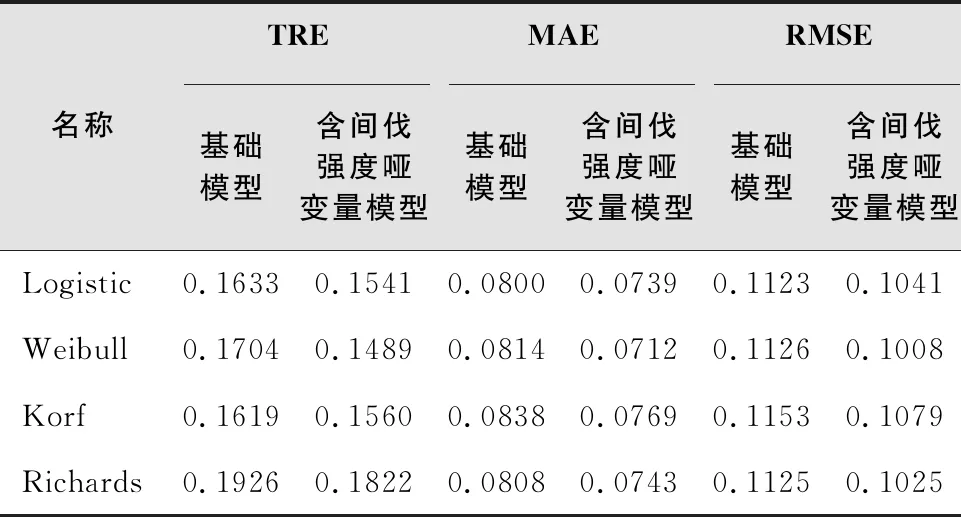
表5 基础模型与含间伐强度哑变量模型拟合效果对比

从表5模型模拟结果可以看出，含间伐强度哑变量模型的TRE、MAE、RMSE检验指标值均小于基础模型的检验指标值。

为更直观地反映基础模型与含间伐强度哑变量模型拟合效果差异，建立断面积残差分布图(图2)和断面积实测值与预测值相关关系图(图3)。

由图2、图3可以看出，含间伐强度哑变量模型要优于基础模型，其拟合效果明显优于基础模型。说明含间伐强度哑变量断面积生长模型模拟效果要优于基础模型的模拟效果，且含间伐强度哑变量的Weibull模型最优。利用F检验对模型进行检验，检验结果F=57.04>F0.95(9，337)=1.91，说明回归效果显著。最优模型为：

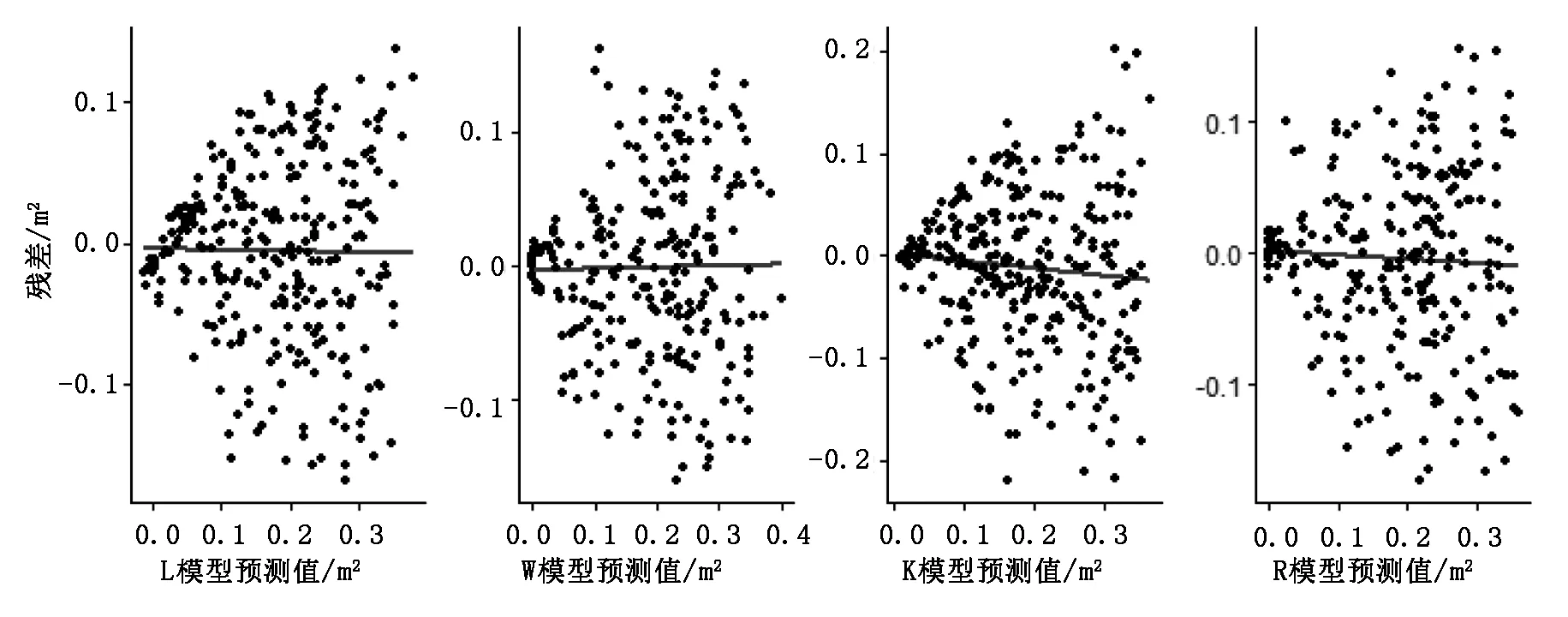
图2 含间伐强度哑变量模型残差Fig.2 Residual Diagram of dummy variable model with thinning intensity

图3 含间伐强度哑变量预测值与实测值相关关系Fig.3 Correlation between predicted value and measured value with dummy variable of thinning intensity

g=(a+c1K1+c2K2)SI[1-exp-(a1+c3K1+c4K2)t(a2+c5K1+c6K2)CI]

5 讨论与结论

5.1 讨论

使用固定半径法确定竞争木时，通常依据树种的不同来研究确定一个合适的竞争半径。本实验将油松竞争半径确定为6.4 m。随着目标树近自然经营在国内的发展，通过目标树竞争距离构建目标树竞争强度与目标树生长关系尤为重要，油松的断面积受竞争强度影响显著，通过目标树与竞争木之间距离的改变，目标树空间分布格局发生变化，林木的空间分布格局直接或间接影响林木生长及林下空间合理分配[25]。随着林木的生长发育导致样地立地条件改变、林木年龄增长、人为采伐等，目标树竞争压力必然会发生变化，在固定半径内的目标树竞争压力变化规律还有待进一步研究。因此通过对目标树竞争距离的研究，可以较好地为森林近自然经营和森林抚育间伐提供更加科学的依据。

目前并没有一个单一的竞争指数或单一类别的指数是普遍优越的，指标的表现因森林类型和立地条件而异[26]。Hegyi简单竞争指数是目前应用比较广泛的一类指标，其从胸径与距离的角度构建了林木之间的竞争关系。有学者研究认为利用树冠重叠指数可以较好地反映竞争关系，因此在进一步研究林木竞争指标中可以综合考虑指标与胸径、树冠、树高之间的相关关系，从而研究林木水平和垂直空间的综合竞争状况。

不同间伐强度的树种结构、径阶结构及对象木、目标树所受的竞争压力均表现出差异性，导致林木生长发育的差异，采用林分尺度上的间伐强度对林木生长发育影响同样显著，但对于单木尺度的间伐强度对油松断面积的影响本实验也做了相关分析，结果并不理想，相关问题有待进一步研究。

含间伐强度哑变量模型可以很好地融合于油松单木模型，提高断面积建模精度，扩大模型的相容性。由于此次研究林木数据有限，缺乏有效的适用性检验，以后的研究中可以在增加样本数量的基础上，研究更多不同类型的单木断面积生长模型，以增加模型的适用范围。

5.2 结论

采用4种理论生长方程建立关帝山油松与距离有关的单木断面积生长基础模型，各基础模型预测精度均在90%以上，预测效果良好。

在考虑林分间伐效应的基础上，将间伐强度作为哑变量引入基础模型，构建含间伐强度哑变量与距离有关的油松单木断面积生长模型，引入哑变量后，各模型预测精度显著提高，其中Weibull模型引入间伐强度哑变量模型拟合度和预测精度最优，分别为0.606 1、99%，TRE、MAE及RMSE检验指标值最小，含间伐强度哑变量的Weibull模型可作为关帝山油松最优单木断面积生长模型，哑变量最优组合方式为a、a1、a2。

本研究建立的模型对关帝山地区油松天然林是适用的，可以模拟其单木的生长，从而为油松林分的经营管理决策提供参考依据。