基于瑞利-里兹法的层状地基应变问题的近似解析解

朱桂春，张雯超，陈胜

(1.苏州大学 轨道交通学院，江苏 苏州 215000；2.扬州工业职业技术学院 建筑工程学院，江苏 扬州 225000；3.中国地质大学(武汉新校区建设指挥部)，湖北 武汉 430074)

0 引 言

土体大多自然沉积，形成层状构造[1-2]，但在工程实践中，一般将土视为均质体，采用弹性模量加权平均方法近似模拟分层土，对其变形特性进行研究，但是这样处理可能会引起建筑物的不均匀沉降[3]，危害建筑物的安全。

对于任意荷载作用下的层状地基应力应变状态求解，可以简化为平面应变问题。平面应变问题是三维空间问题的一种特殊情况，即假定y轴方向无位移，研究层状地基平面应变问题具有一定的现实意义，如在层状地基中开挖地连墙槽段，槽壁受侧向静止土压力与泥浆压力的共同作用，可简化为受三角形水平分布荷载作用的平面应变问题求解地层的变形情况。

目前求解层状结构的方法主要有位移函数法[4-7]、柔度矩阵法[8-12]、传递矩阵法[13-14]、精确的刚度矩阵法[15-17]和解析层元法[18]等。已有层状结构求解方法中，传递矩阵法计算时数据溢出，而刚度矩阵法中的矩阵元素表达式复杂，不便于实际应用。

本文利用Mathematica软件计算程序，基于扩展的瑞利-里兹法分析层状地基应变问题的近似解答，推导非对称荷载作用下层状地基平面应变问题的解答，以及各参数对变形的敏感性，以期为类似工程的设计与施工提供参考。

1 各向同性地基近似解析解的推导

1.1 各向同性地基平面问题的基本关系式

各向同性体的胡克定律为

(1)

式中,λ=E/[(1+v)(1-2v)]。

1.2 推导思路

应变的近似解析解求解思路(瑞利-里兹法)如下：

(1)假定任一层状区域内任一点的水平位移为u(x,z)，竖直位移为v(x,z)。

(2)构造泛函

(3)据最小势能原理，对泛函进行变分，求其驻值，同时考虑边界条件约束，求解待定参数。

对于地表以下受水平非对称荷载作用的层状各向同性土体，由于结构复杂，参数较多，使用传统的瑞利-里兹法求解，积分难度较大，难以得出正确的结果。为求解方便，节省计算时间，将层状各向同性土体划分为多层有限区域和无限区域，有限区域与无限区域位移采用有理多项式假定，将每层土体作为一个块体，利用扩展的瑞利-里兹法对其进行近似解析解求解，区域示意图见图1。

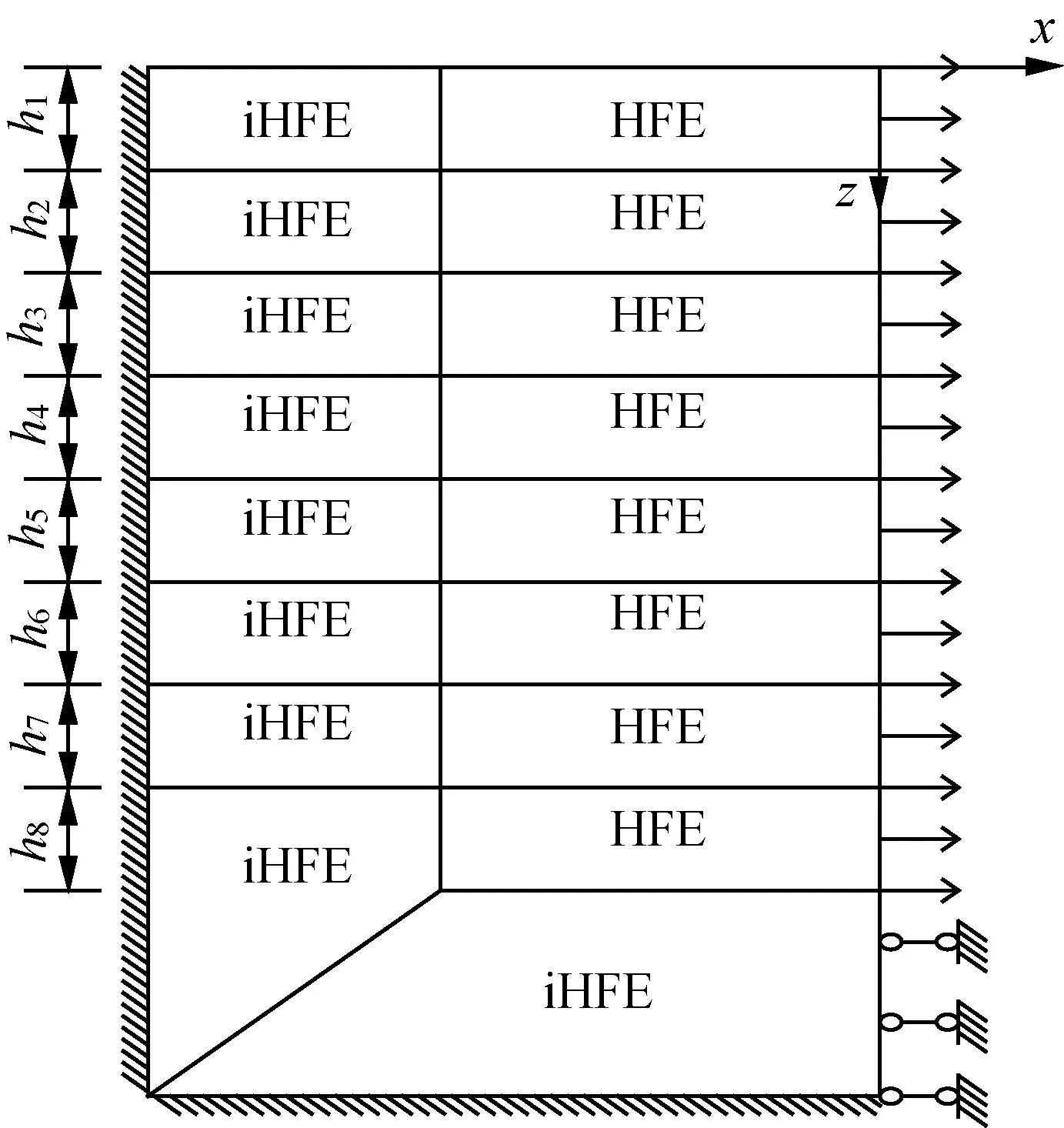
图1 各向同性地基分层示意图

假定土层为各向同性土层，各层层厚分别为h1，h2，h3，…，hn，HFE为有限区域，iHFE为无限区域，模型右侧边界一定深度内受荷载作用，其余深度土层右侧边界受水平位移约束。左侧及下部边界为无穷远处。

经验证，标准瑞利-里兹法中的位移假定函数

w=C0+C1x+C2x2+C3x3，

(3)

等价于

w=N1(x)wi+N2(x)θi+N3(x)wj+
N4(x)θj，

(4)

两者待定系数个数相同，Ni为插值基或形函数。

同理可知，二维位移函数

(5)

等价于

w=N1(ξ,η)w1+N2(ξ,η)w2+N3(ξ,η)w3+
N4(ξ,η)w4，

(6)

式中：N1=(1-ξ)(1-η)/4；N2=(1+ξ)(1-η)/4；N3=(1+ξ)(1+η)/4；N4=(1-ξ)(1+η)/4。

1.3 有限部分推导

为提高假定的多项式精度，可增加待定系数的个数，如

w=C0+C1ξ+C2η+C3ξη+C4ξ2+C5η2+C6ξ3+
C7ξ2η+C8ξη2+C9η3……+Cnξmηm， (7)

可等价假定为

(8)

在[-1,1]×[-1,1]区域内,ξ轴上投影n个坐标，η轴上投影n个坐标，从下向上第i行，从左向右第j列的节点号对应的形式数为Nij=Ni(η)×Nj(ξ)，节点标号顺序如图2所示。

图2 节点投影示意图

Ni为ξ轴[-1,1]内，n个点构成一维拉格朗日插值基，

式中：-1=ξ1<ξ2<ξ3…<ξn=1；ξi的分布符合扩展切比雪夫多项式零点分布。同理Nj将ξ替换成η即可,式(8)假定完毕。它的多项式成分可以从帕斯卡三角形中去数n项。

由于以上假定都是基于[-1,1]×[-1,1]范围的单位坐标系，而地层结构建立在x-z坐标系内，因此可引入坐标变换，建立(x-z)与(ξ-η)之间的一一对应关系。可认为x与z都是(ξ，η)的函数，即x=x(ξ，η)，z=z(ξ，η)，则该函数不唯一，只要连续、一一对应即可，最简单的关系为多项式关系，有限区域的坐标变换见图3。

图3 有限区域坐标变换

则有

基于以上分析，一切均可用(ξ-η)坐标描述，方便后续计算。

(11)

若(ξ-η)坐标可对应得(x-z)坐标及u,v；根据上述位移模式，可利用最小势能原理：

(12)

根据几何方程：

(13)

对其插值得

(14)

由于Nu，Nw为关于ξ，η的函数，不可直接求关于x，z的偏导，借助链式法则有

(15)

即

(16)

记

(18)

于是，式(14)中的B矩阵便可解出，从而根据[σ]=[D]·[ε]=[D][B]·[δe]，与1.1中，D含义是否相同

(19)

将应变[ε]根据最小势能原理代回,可得

(20)

节点位移矩阵

由于δδe的任意性，式(12)等价为

经多次调试，尽量平衡计算时间与计算精度，文中式(7)采用8次多项式假定。

1.4 无限部分推导

无限部分形函数与有限部分中一致，节点编号也一致，但其坐标变换有所不同，如图4所示。

图4 无限区域坐标变换

满足两坐标系下的同号节点一一对应，则有

(23)

可见，①②③④围成的区域为内映射，其他区域为外映射，可检验其正确性。坐标变换时，仅需①②③④点的坐标，不需要指定无穷远处的坐标。为建模方便，可以形式上指定无穷远节点坐标，方便查看，实际计算不会影响。

由于无限区域与有限区域采用相同的节点插值和自由度，所以在单元组装时，将它们视为相同的单元,即K1=K有限，K2=K无限，这样就可以考虑两种单元共节点的情况，自动满足两者交界处变形协调。

2 模型验证

为验证近似解析解计算结果的准确性，本文采用MIDAS/GTS有限元模型进行验证。

2.1 单层各向同性地基的验证

模型设置如图5所示。

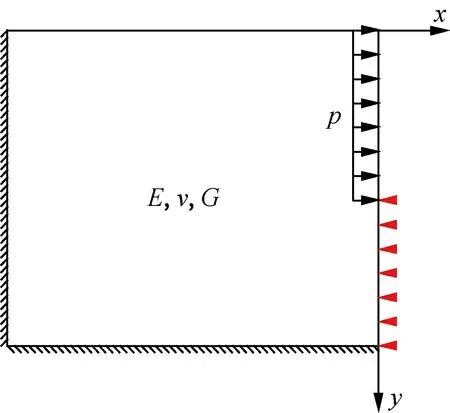
图5 单层地基计算模型图

由于近似解析解计算程序可实现对无穷远处边界的高精度描述。为了保证验证的准确性，将MIADAS有限元地基模型范围设置为136 m×136 m，左侧与底部边界受法向位移约束，右侧边界上部受x向均布荷载p作用，p=10 kPa，作用深度D=8 m，右侧边界下部受法向位移约束；而近似解析解计算模型右侧边界约束条件同有限元模型，左侧及底部边界为无限边界，为方便与有限元计算结果进行比对，近似解析解计算程序模型范围为136 m×12 m，有限及无限区域的划分如图1所示,其中有限区域范围为100 m×8 m。横观各向同性地基弹性参数分别为E=20 MPa，v=0.25，G=8 MPa。

近似解析解计算程序与MIDAS/GTS有限元软件计算结果如图6～7所示。其中土体水平位移取右侧边界节点，竖向位移取上部边界节点，下同。由图6～7可以看出，两者结果吻合度较高，说明本文所用理论的正确性和程序计算的准确性，可满足精度要求。

图6 验证例水平位移对比

图7 验证例竖向位移对比

2.2 层状各向同性地基的验证

为验证近似解析解在层状地基中的适用性，本文对水平向均布荷载作用下三层各向同性地基进行求解，计算模型如图8所示。

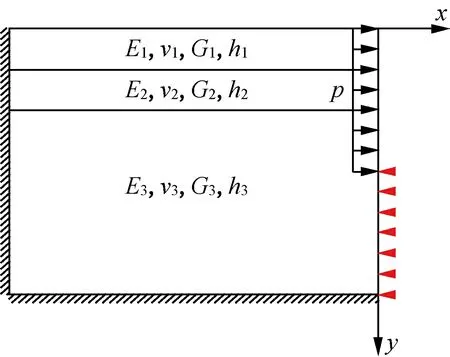
图8 多层地基计算模型图

MIADAS有限元地基模型范围设置为136 m×136 m，左侧与底部边界受法向位移约束，右侧边界上部受x向均布荷载p作用，p=10 kPa，作用深度D=8 m，右侧边界下部受法向位移约束，而近似解析结计算模型右侧边界约束条件同有限元模型，左侧及底部边界为无限边界，近似解析解计算模型如2.1节。有限元模型各层地基弹性参数如表1所示。

表1 各地层参数

将求解结果与MIDAS/GTS计算的结果对比，如图9～10所示。从图9～10可以看出，各点吻合度较高，说明本计算程序在求解层状各向同性地基变形依然具有较高的准确性和计算精度。

图9 层状地基验证例水平位移对比

图10 层状地基验证例竖向位移对比

对本文计算程序和MIDAS/GTS软件响应速度进行对比，测试操作系统版本：Win7旗舰版Service Pack1 64位；CPU版本：AMD A8-7650K Radeon R7 3.3 Ghz；内存：8.00 GB。经测试，本文计算程序计算时间约17.5 s，MIDAS/GTS软件计算时间为11.68 s，但本文计算程序在工况发生变化时，参数输入简便，可自动重新划分网格，设置边界条件，较传统的有限元软件建模时间大幅缩短，操作更为便捷。

3 土的分层特性对位移的影响

由以上分析可知，对地层变形敏感度较高的参数为弹性模量，所以下述算例考虑层状均质地基在水平荷载作用下每层弹性参数不同对地层变形的影响，主要控制变量为各层的弹性模量E。

算例模型尺寸及边界条件同2.1节，土体分为5层，有限区域各层地基E,v,h如表2所示。各工况地层分布如表3所示。

表2 各地层参数

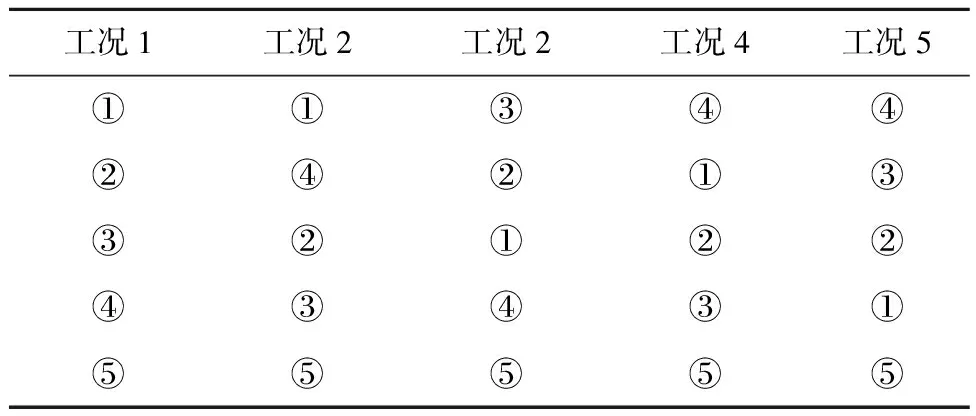
表3 各工况地层分布

另外增加工况6，工况6为均质地基，采用模量与深度的加权平均近似模拟分层土的特性，其弹性参数E由式(24)计算。各工况位移如图11～12所示。

(24)

由图11～12可以看出，不同工况下的地基水平位移和竖向位移明显不同，土的分层特性对地基的位移有显著影响：上层土的物理性质对整体的变形影响较大，上层土的弹性模量越大，其水平及竖向的最大位移越小。对比工况1～5和工况6可以看到，在相同的外部荷载及边界条件下，分层地基与均质地基的位移变化差异较大，因此，工程实践中将土层视为各项同性的均质体，采用模量与深度的加权平均近似模拟分层土的特性进行设计计算的方法是不妥当的。

图12 各工况竖向位移

4 结 论

(1)本文基于扩展的瑞利-里兹法分析层状地基应变问题的近似析解，求解过程采用高阶多项式和无穷坐标变换,实现了对无穷远处边界的高精度描述，克服了传统有限元方法对无穷远处结构盲目截断的缺点。

(2)层状结构对地基变形有较大影响，其中上层土的物理性质对整体的变形影响较大，工程实践中常规的将土层视为各项同性的均质体，采用模量与深度的加权平均近似模拟分层土的特性进行设计计算的方法是不妥当的，所以在工程实际应用中考虑土的分层特性是十分必要的。